当前位置：首页 > 编程日记 > 正文

pytorch中tensor.mul()和mm()和matmul()

编程日记 2024-06-08 10:30:00

tensor.mul

tensor.mul和tensor * tensor 都是将矩阵的对应位置的元素相乘，因此要求维度相同，点乘
torch.mul(input, other, *, out=None) → Tensor
参数：
input (Tensor) – the input tensor.
other (Tensor or Number)

torch.mul(input, other)是将input和other的对应位相乘，other可以是张量，可以是数字。
torch.mul(input, other)中input和bother维度相等，但是，对应维度上的数字可以不同，可以用利用广播机制扩展到相同的形状，再进行点乘操作。

tensor = torch.ones(4, 4)
tensor[:,1] = 0
print(tensor)

tensor([[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.]])

点乘示例：

print(f"tensor.mul(tensor) \n {tensor.mul(tensor)} \n")
print(f"tensor * tensor \n {tensor * tensor} \n")
print(f"torch.mul(tensor,100) \n {torch.mul(tensor,10)} \n")
print(f"torch.mul(tensor*2,tensor) \n {torch.mul(tensor*2,tensor)} \n")

输出：

tensor.mul(tensor) tensor([[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.]]) tensor * tensor tensor([[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.],[1., 0., 1., 1.]]) torch.mul(tensor,100) tensor([[10.,  0., 10., 10.],[10.,  0., 10., 10.],[10.,  0., 10., 10.],[10.,  0., 10., 10.]]) torch.mul(tensor*2,tensor) tensor([[2., 0., 2., 2.],[2., 0., 2., 2.],[2., 0., 2., 2.],[2., 0., 2., 2.]])

tensor.mm

torch.mm(input, mat2, *, out=None) → Tensor
参数：
input (Tensor) – the first matrix to be matrix multiplied
mat2 (Tensor) – the second matrix to be matrix multiplied
vector1 x vector2 矩阵乘法
如果input是(n×m) 维, mat2 是(m×p) 维, 输出就是(n×p) 维.
torch.mm(a, b)是矩阵a和b矩阵相乘，比如a的维度是(3, 4)，b的维度是(4, 2)，返回的就是(3, 2)的矩阵torch.mm(a, b)针对二维矩阵

print(f"tensor.mm(tensor.T) \n {tensor.mm(tensor.T)} \n")
print(f"torch.mm(tensor,tensor.T) \n {tensor @ tensor.T} \n")
print(f"tensor @ tensor.T \n {tensor @ tensor.T} \n")

输出：

tensor.mm(tensor.T) tensor([[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.]]) torch.mm(tensor,tensor.T) tensor([[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.]]) tensor @ tensor.T tensor([[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.],[3., 3., 3., 3.]])

tensor.matmul

torch.matmul( input , other , * , out = None ) → Tensor
两个张量的矩阵乘积。

操作取决于张量的维度，如下所示：

如果两个张量都是一维的，则返回点积（标量）。
如果两个参数都是二维的，则返回矩阵-矩阵乘积。
如果第一个参数是一维的，而第二个参数是二维的，则为了矩阵乘法的目的，在其维度前面加上 1。矩阵相乘后，前面的维度被删除。
如果第一个参数是二维的，第二个参数是一维的，则返回矩阵向量乘积。
如果两个参数至少是一维的并且至少一个参数是 N 维的（其中 N > 2），则返回一个批处理矩阵乘法。如果第一个参数是一维的，为了批量矩阵乘法的目的，在其维度前面加上 1 并在之后删除。如果第二个参数是一维的，则为了批处理矩阵倍数的目的，将 1 附加到其维度并在之后删除。非矩阵（即批次）维度被广播（因此必须是可广播的）。例如，如果input是 ( j×1×n×ñ ）张量并且other是( k×n×ñ ）张量，out将是( j×k×n×ñ ）张量。

请注意，广播逻辑在确定输入是否可广播时仅查看批次维度，而不是矩阵维度。例如，如果input是 ( j×1×n×m)张量并且other是( k×m×p ）张量，即使最后两个维度（即矩阵维度）不同，这些输入也可用于广播。out将是一个( j×k×n×p ）张量。

此运算符支持TensorFloat32。

# vector x vector
tensor1 = torch.randn(3)
tensor2 = torch.randn(3)
torch.matmul(tensor1, tensor2).size()
# # torch.Size([])# matrix x vector
tensor1 = torch.randn(3, 4)
tensor2 = torch.randn(4)
torch.matmul(tensor1, tensor2).size()
# # torch.Size([3])# vector x matrix
tensor1 = torch.randn(4) # 1*4
tensor2 = torch.randn(4, 3)
print(torch.matmul(tensor1, tensor2).size())
# # torch.Size([3])# batched matrix x broadcasted vector
tensor1 = torch.randn(10, 3, 4) # 30*4
tensor2 = torch.randn(4) # 4*1
torch.matmul(tensor1, tensor2).size()
# # torch.Size([10, 3])# batched matrix x batched matrix
# 将b的第0维broadcast成10提出来，后两维做矩阵乘法即可。
tensor1 = torch.randn(10, 3, 4) # 10, 3*4
tensor2 = torch.randn(10, 4, 5) # 10, 4*5
torch.matmul(tensor1, tensor2).size()
# # torch.Size([10, 3, 5])# batched matrix x broadcasted matrix
tensor1 = torch.randn(10, 3, 4) # 30*4
tensor2 = torch.randn(4, 5) # 4*5
torch.matmul(tensor1, tensor2).size()
# # torch.Size([10, 3, 5])

https://www.dkcj.cn/info/9798.html

pytorch中tensor.mul()和mm()和matmul()

tensor.mul

tensor.mm

tensor.matmul

相关文章：

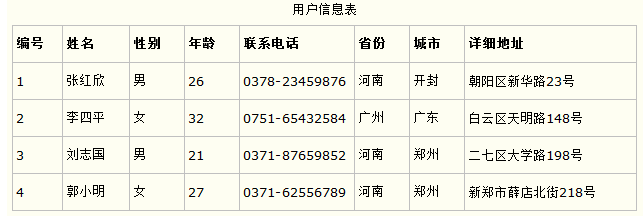
python学习笔记 day44 数据库三范式

行内标签（最常用的：a标签、img标签、span标签）

SAP HR模块配置假期日历和缺勤类型

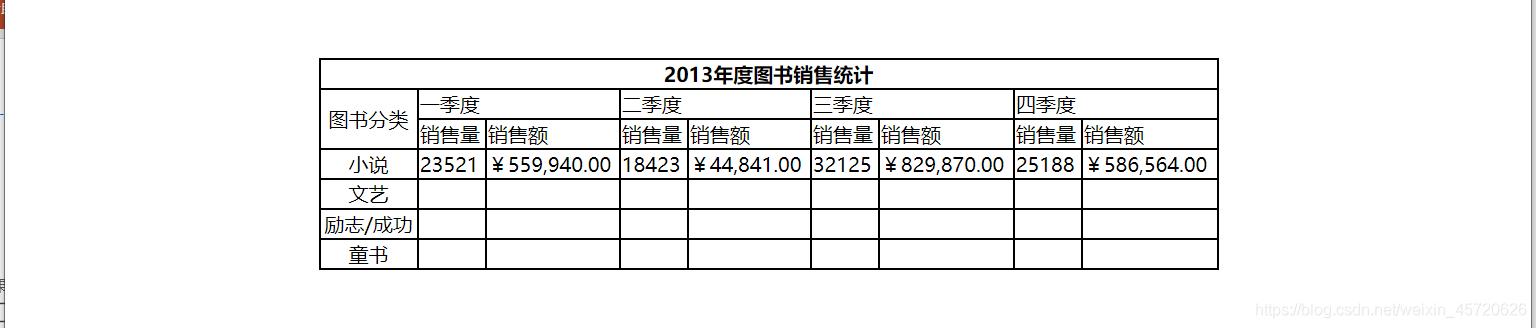
表格(table、tr、th、td、colspan、rowspan)

Java基础概念性的知识总结

vue里的数据

【Leetcode】刷题之路2（python）

ORA-01113 file 1 needs media recovery

大数据批量导入，解决办法，实践从定时从 sqlserver 批量同步数据到 mySql

【目标检测】yolo系列：从yolov1到yolov5之YOLOv5训练自己数据集（v6.0）

CSS之常用选择器（元素、id、类、通配选择器）

Java中实体类 VO、 PO、DO、DTO、 BO、 QO、DAO、POJO的概念

SAP有用的NOTE（持续更新）

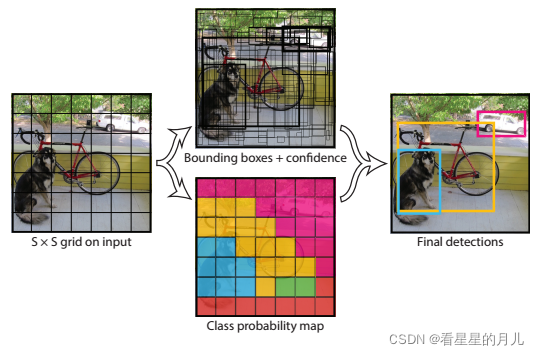
【目标检测】yolo系列：从yolov1到yolov5之YOLOv1详解及复现

Ubuntu终端命令行缩短显示路径

主要的约瑟夫环问题

CSS之复合选择器（交集、并集选择器）

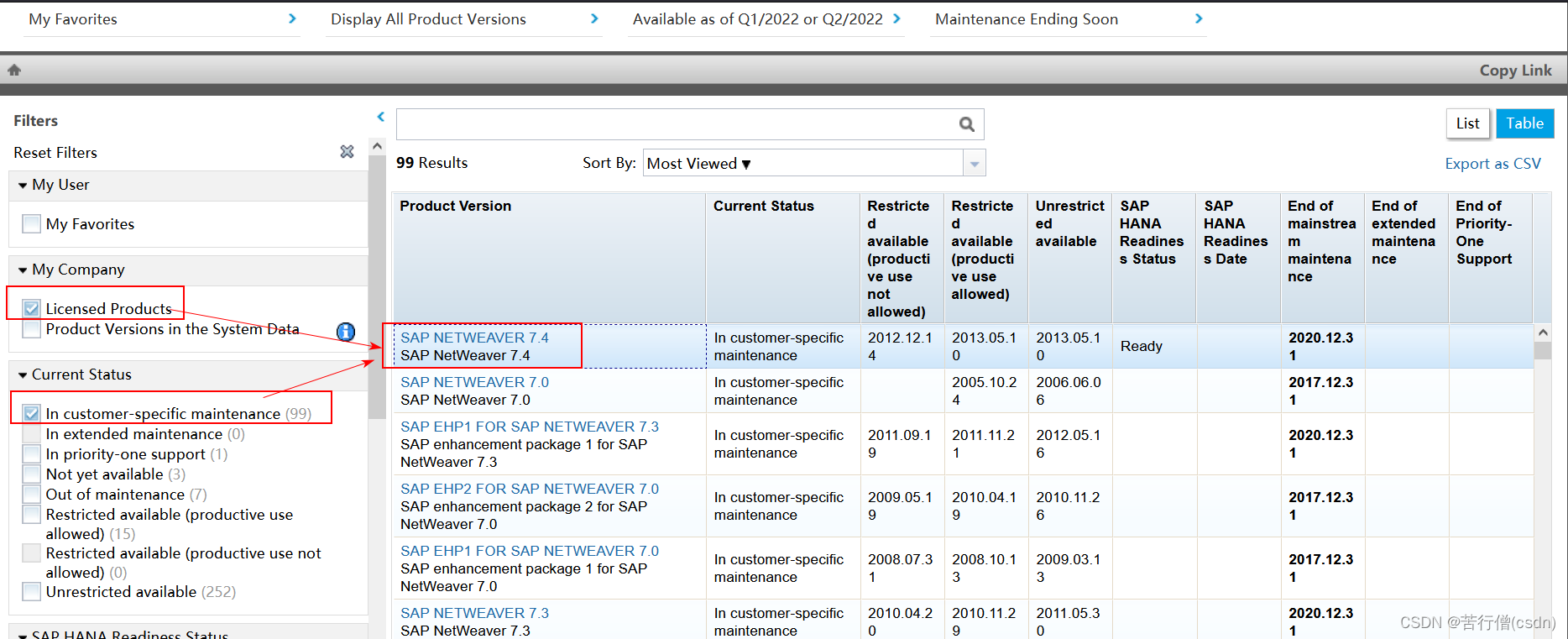
SAP有用的知识（持续更新）

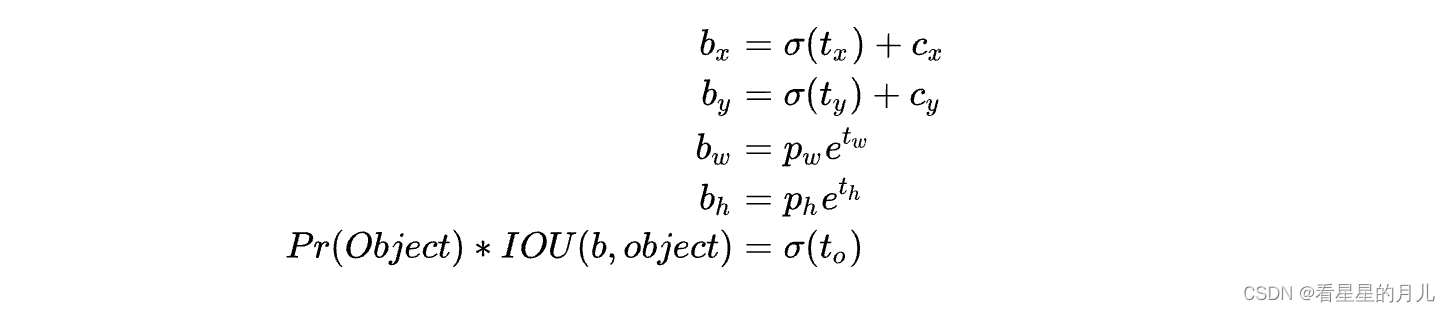
【目标检测】yolo系列：从yolov1到yolov5之YOLOv2详解及复现

我有一个很好的思维习惯-反思

CSS之关系选择器（子元素、后代、兄弟选择器）

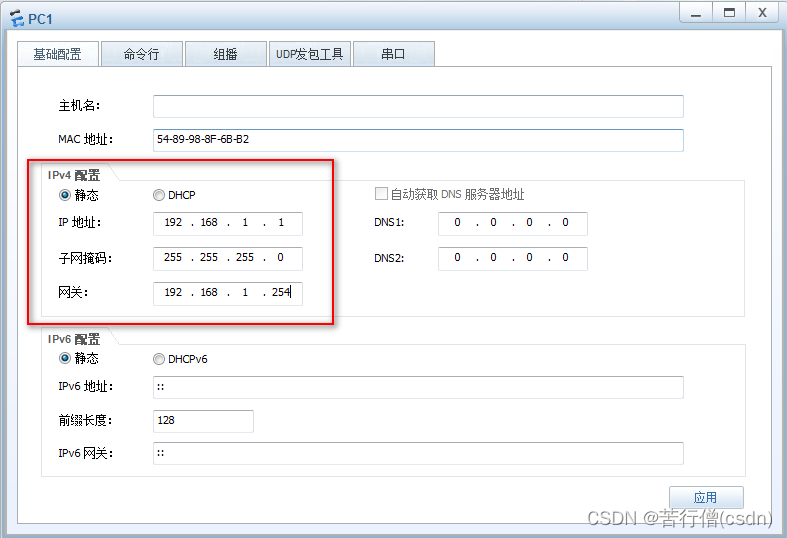
网络管理员比赛回顾01-基本操作和简单vlan

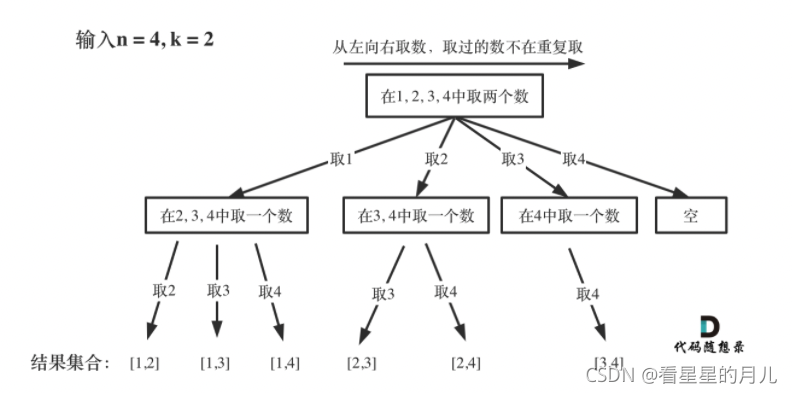
【Leetcode】刷题之路3（python版）

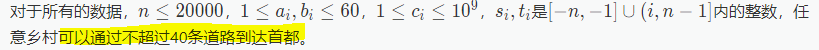
Luogu 4438 [HNOI/AHOI2018]道路

52深入理解C指针之---不透明指针

CSS之布局（文档流）

网络管理员比赛回顾02-网关、静态路由、动态路由

[模拟]纺车的轮子 Spinning Wheels

从头理解self-attention机制

筛选法求N以内的所有素数