【Leetcode】刷题之路2(python)
哈希映射类题目(简单题小试牛刀啦bhn)
- 242.有效的字母异位词
- 349.两个数组的交集
- 1002.查找常用字符
- 202.快乐数
- 383.赎金信
242. 有效的字母异位词
用python的Counter类太绝了!!!
一行代码解决问题,这道题实际上就是比较两个字符串的每个字母数是不是一样。
在刷题之路1的最后我列出了collections模块的几个字典的子类
Counter:字典的子类,提供了哈希对象的计数功能
class Solution:def isAnagram(self, s: str, t: str) -> bool:return Counter(s)==Counter(t)
349. 两个数组的交集
思路:
1.先把nums1和nums2转为集合
2.两集合求交集
3.再把交集转化为list
class Solution(object):def intersection(self, nums1, nums2):return list(set(nums1) & set(nums2))
1002. 查找常用字符
给你一个字符串数组 words ,请你找出所有在 words 的每个字符串中都出现的共用字符( 包括重复字符),并以数组形式返回。你可以按任意顺序 返回答案。
题解
利用python内置模块一行代码解决问题:求每个计数器的交集即可
解释:
Counter类
Counter类基于dict字典类,可使用dict的方法,其实例可以进行 与 或 非 异或 运算。map
map(function, iterable, …):会根据提供的函数对指定序列做映射。第一个参数 function 以参数序列中的每一个元素调用 function 函数,返回包含每次 function 函数返回值的新列表。reduce
reduce(function, iterable[, initializer]):对迭代器内进行两个元素操作并传递。
求每个计数器的交集即可,而这个交集必须与其后的交集传递下去,因此 reduce 函数满足。即这里求两个 Counter 计数器的交集操作,然后作为参数 x 传递到下一个去和 iterable 下一个计数器取交集。由于 reduce 最后运算得到的是 Counter 对象,因此取出元素 Counter.elements() 是迭代器,因而 list 创建列表。
class Solution:def commonChars(self, A: List[str]) -> List[str]:return reduce(lambda x, y: x&y, map(Counter, A)).elements()# 使用 lambda 匿名函数
代码详细展开如下:
class Solution:def commonChars(self, A: List[str]) -> List[str]:from collections import Counterans = Counter(A[0])for i in A[1:]:ans &= Counter(i)return list(ans.elements())
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
题解
方法一:哈希集合检测循环
我们可以先举几个例子,找出快乐数的规律,发现有三种可能性:
- 最终会得到 1。
- 最终会进入一个循环。
- 值会越来越大,最后接近无穷大。(但经过验证不存在)
所以要么是快乐数,要么会进入一个循环。
思路:
算法分为两部分,我们需要设计和编写代码。
- 给一个数字 nn,它的下一个数字是什么?
- 按照一系列的数字来判断我们是否进入了一个循环。
实现:
第 1 部分我们按照题目的要求做数位分离,求平方和。
第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时,我们都会检查它是否已经在哈希集合中。
- 如果它不在哈希集合中,我们应该添加它。
- 如果它在哈希集合中,这意味着我们处于一个循环中,因此直接返回 false。
(注!我们使用哈希集合而不是向量、列表或数组的原因是因为我们反复检查其中是否存在某数字。检查数字是否在哈希集合中需要 O(1) 的时间,而对于其他数据结构,则需要 O(n) 的时间。选择正确的数据结构是解决这些问题的关键部分。)
函数divmod(dividend, divisor)是Python的内置函数,它可以把除数和余数运算结果结合起来,返回一个包含商和余数的元组(a / b, a % b)。
def isHappy(self, n: int) -> bool:def get_next(n):total_sum = 0while n > 0:n, digit = divmod(n, 10)total_sum += digit ** 2return total_sumseen = set()while n != 1 and n not in seen:seen.add(n)n = get_next(n)return n == 1
复杂度分析
时间复杂度:时间复杂度:O(243⋅3+logn+loglogn+logloglogn)… = O(logn)。
空间复杂度:O(\log n)O(logn)。
方法二:快慢指针法
通过反复调用 getNext(n) 得到的链是一个隐式的链表。隐式意味着我们没有实际的链表节点和指针,但数据仍然形成链表结构。起始数字是链表的头 “节点”,链中的所有其他数字都是节点。next 指针是通过调用 getNext(n) 函数获得。
意识到我们实际有个链表,那么这个问题就可以转换为检测一个链表是否有环。因此我们在这里可以使用弗洛伊德循环查找算法。
这个算法是两个奔跑选手,一个跑的快,一个跑得慢。在龟兔赛跑的寓言中,跑的慢的称为 “乌龟”,跑得快的称为 “兔子”。如果有环的话,不管乌龟和兔子在循环中从哪里开始,它们最终都会相遇。这是因为兔子每走一步就向乌龟靠近一个节点(在它们的移动方向上)。
算法
我们不是只跟踪链表中的一个值,而是跟踪两个值,称为快跑者和慢跑者。在算法的每一步中,慢速在链表中前进 1 个节点,快跑者前进 2 个节点(对 getNext(n) 函数的嵌套调用)。
- 如果 n 是一个快乐数,即没有循环,那么快跑者最终会比慢跑者先到达数字 1。
- 如果 n 不是一个快乐的数字,那么最终快跑者和慢跑者将在同一个数字上相遇。
def isHappy(self, n: int) -> bool: def get_next(number):total_sum = 0while number > 0:number, digit = divmod(number, 10)total_sum += digit ** 2return total_sumslow_runner = nfast_runner = get_next(n)while fast_runner != 1 and slow_runner != fast_runner:slow_runner = get_next(slow_runner)fast_runner = get_next(get_next(fast_runner))return fast_runner == 1
时间复杂度:O(logn)
空间复杂度:O(1),对于这种方法,我们不需要哈希集来检测循环。
383. 赎金信
为了不在赎金信中暴露字迹,从杂志上搜索各个需要的字母,组成单词来表达意思。
给你一个赎金信 (ransomNote) 字符串和一个杂志(magazine)字符串,判断 ransomNote 能不能由 magazines 里面的字符构成。如果可以构成,返回 true ;否则返回 false 。
magazine 中的每个字符只能在 ransomNote 中使用一次。
题解
使用Counter类的交集操作,获得交集,判断两者交集是否等于ransomNote,是则满足,否则不满足。(Counter yyds!)
class Solution:def canConstruct(self, ransomNote: str, magazine: str) -> bool:a = Counter(ransomNote) b = Counter(magazine)return (a & b) == a
用内存换时间!!!
总结
python的哈希类题目,可以多多考虑collections模块下的counter子类,counter提供了哈希对象的计数功能
相关文章:

ORA-01113 file 1 needs media recovery
启动数据库时报错。ORA-01113 datafile1需要恢复。 rman执行恢复。恢复后尝试打开数据库,看结果 rman target / recover datafile 1; alter database open; 反复上述过程,直到所有数据文件恢复。 recover datafile 1; …… recover datafile 13; 如果…

大数据批量导入,解决办法,实践从定时从 sqlserver 批量同步数据到 mySql
c#代码,批量导入数据代码 public class MySql_Target : ZFCommon.DataAccesser.Base.DABase{public MySql_Target(){this.InitDataAccesser(ZFCommon.DataAccesser.DatabaseType.MySql, ReadConfig.TargetConnection);}///大批量数据插入,返回成功插入行数 /// <…

【目标检测】yolo系列:从yolov1到yolov5之YOLOv5训练自己数据集(v6.0)
一、源码下载及requirments 源码下载地址:https://github.com/ultralytics/yolov5 (持续更新中) 本人所用环境如下: pytorch:1.8(因为cuda版本用了pytorch1.8) cuda:10.1 Python&am…

CSS之常用选择器(元素、id、类、通配选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*1、元素选择器作用:根据标签名来选中指定的元素语法:标签名{}例子:p{} h1{} div{}*//*p{color: red;}*/…

Java中 实体类 VO、 PO、DO、DTO、 BO、 QO、DAO、POJO的概念
PO(persistant object) 持久对象 在 o/r 映射的时候出现的概念,如果没有 o/r 映射,没有这个概念存在了。通常对应数据模型 ( 数据库 ), 本身还有部分业务逻辑的处理。可以看成是与数据库中的表相映射的 java 对象。最简单的 PO 就是对应数据库中某个表中…
SAP有用的NOTE(持续更新)
目录 2421240 - Portal is not loaded on Chrome 56 or higher. 66971 - Supported SAP GUI platforms 66971 - Supported SAP GUI platforms 1999880 - FAQ: SAP HANA System Replication 2250144 - FAQ: SAP HANA Secure User Store 2222200 - FAQ: SAP HANA Network …
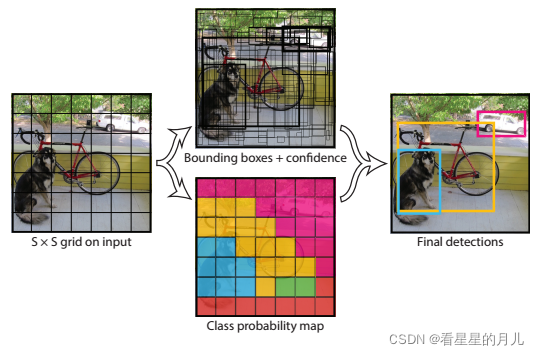
【目标检测】yolo系列:从yolov1到yolov5之YOLOv1详解及复现
检测器通常能够被分为两类,一类是two-stage检测器,最具代表的为faster R-CNN;另一类是one-stage检测器,包括YOLO,SSD等。一般来说,two-stage检测器具有高定位和识别准确性,而one-stage则有速度上…

Ubuntu终端命令行缩短显示路径
平时我们使用linux终端命令行的时候,常常会被一个问题困扰,那就是文件路径过长, 有时候甚至超过了一行,这样看起来非常别扭,其实只要两步就可以解决这个问题: 1,修改.bashrc文件(用户…

主要的约瑟夫环问题
解说 http://poj.org/problem?id3517 n个人,编号为1~n。每次从1開始数,数到m的人出圈。最后一个出圈的人的编号。f[1] 0; for(int i 2; i < n; i) {f[i] ( f[i-1] m)%i; } printf("%d\n",f[n]1);这里第一次出圈的人的编号是mÿ…

CSS之复合选择器(交集、并集选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*将class为red的元素设置为红色*/.red{color: red;}/*将class为red的div字体大小设置为30px*//*1、交集选择器作用:选中同时复合多…
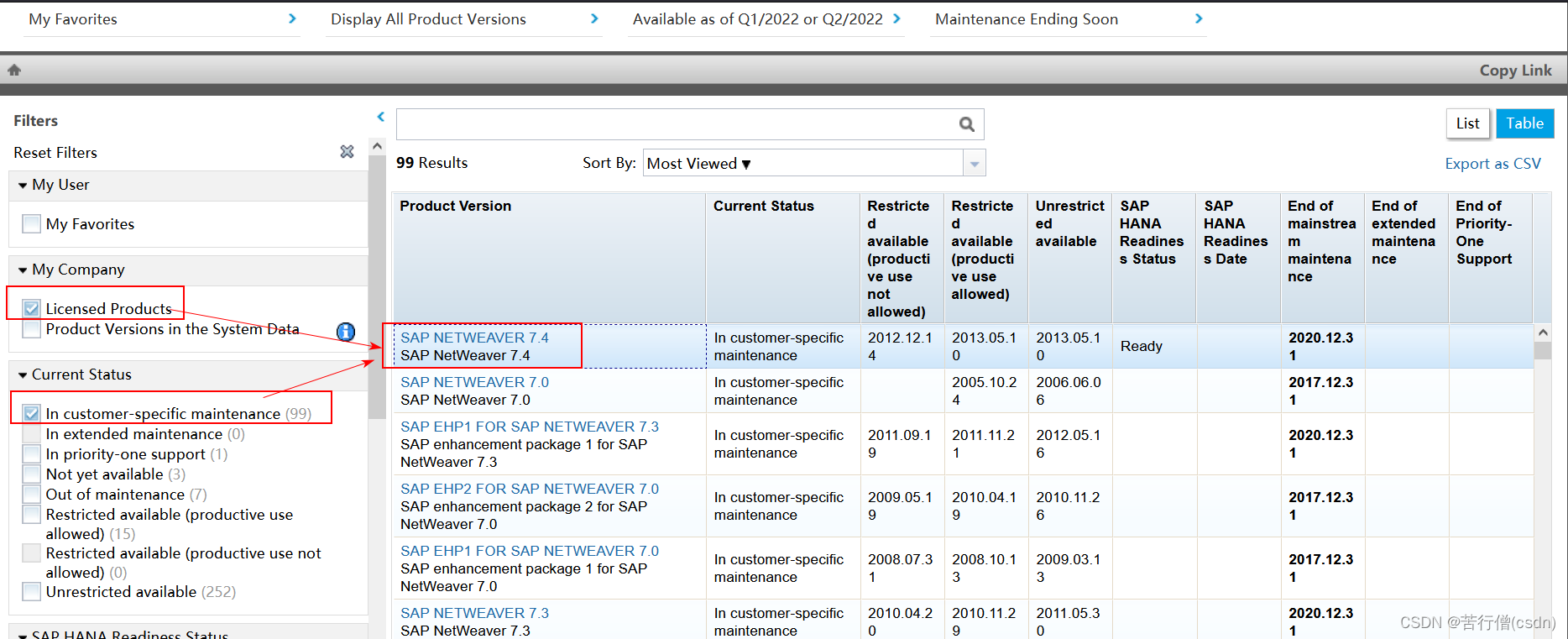
SAP有用的知识(持续更新)
一、安装SAP 1.1、产品可用性矩阵(Product Availability Matrix) SAP官网-Maintenance-Product Availability Matrix,点击页面的Access the Product Availability Matrix。 选中你公司授权的商品(Licensed Products)…
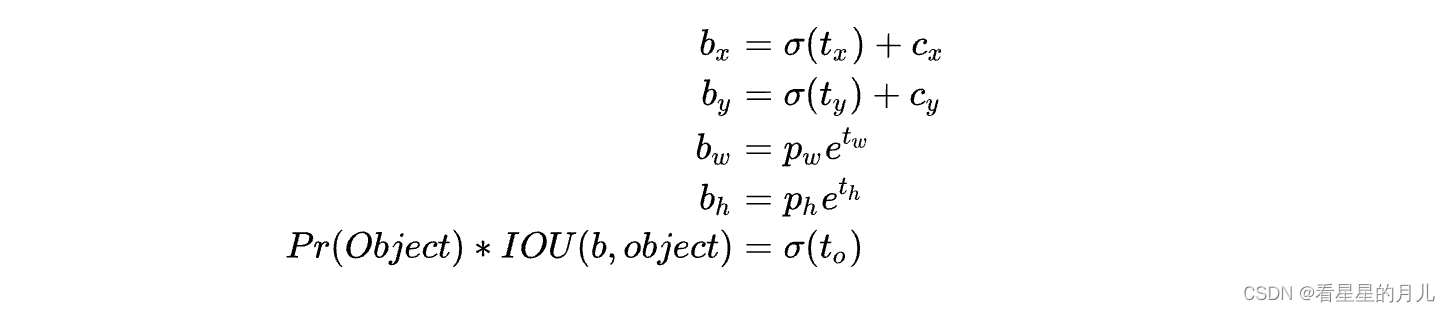
【目标检测】yolo系列:从yolov1到yolov5之YOLOv2详解及复现
YOLO v2 Yolov2论文链接:YOLO9000: Better, Faster, Stronger yolov2的改进 从Yolov2论文的标题可以直观看到就是Better、Faster、Stronger。Yolov1发表之后,计算机视觉领域出现了很多trick,例如批归一化、多尺度训练等等,v2也…

我有一个很好的思维习惯-反思
和我共事过的同事有的会说我聪明,我就暂且当做是夸奖吧,其实我并不是聪明,只是有一个思维习惯。做事过程中或者做完一件事之后会反思这个过程,有哪些地方我是重复操作的,有没有什么地方可以简化流程的,这应…

CSS之关系选择器(子元素、后代、兄弟选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*为div的子元素span设置一个字体颜色*//*子元素选择器:作用:选中指定父元素的指定子元素语法:父元素>子…
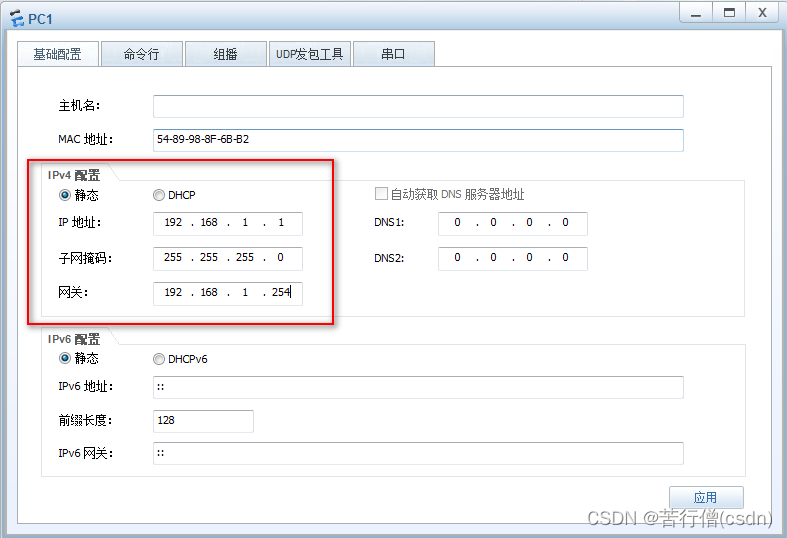
网络管理员比赛回顾01-基本操作和简单vlan
目录 一、模拟器eNSP 二、基本操作 三、配置IP地址 四、VLAN 一、模拟器eNSP 使用eNSP模拟器,来源于网络上的安装包,学习一个。基本操作就不多说了,在实践里慢慢记录 二、基本操作 认识3种视图:用户视图、系统视图、接口视…
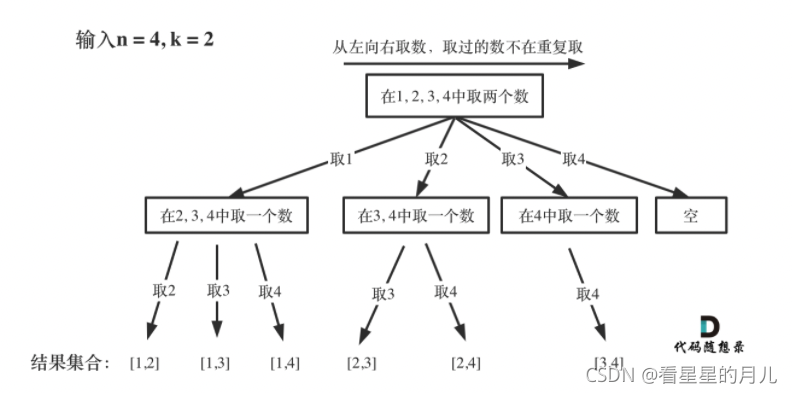
【Leetcode】刷题之路3(python版)
回溯专题 1.回溯算法的本质是n叉树的深度优先搜索,同时,需要注意剪枝减少复杂度。 2.回溯算法三部曲 确定参数和返回值回溯函数终止条件单层循环 3.回溯法思路 回溯法是一种算法思想,而递归是一种编程方法,回溯法可以用递归来…
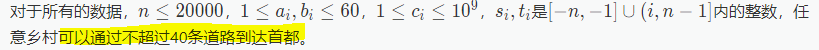
Luogu 4438 [HNOI/AHOI2018]道路
$dp$。 这道题最关键的是这句话: 跳出思维局限大胆设状态,设$f_{x, i, j}$表示从$x$到根要经过$i$条公路,$j$条铁路的代价,那么对于一个叶子结点,有$f_{x, i, j} c_x * (a_x i) * (b_x j)$,对于内部结点…

52深入理解C指针之---不透明指针
该系列文章源于《深入理解C指针》的阅读与理解,由于本人的见识和知识的欠缺可能有误,还望大家批评指教。一、size_t:用于安全表示长度,所有平台和系统都会解析成自己对应的长度 1、定义:size_t类型表示C中任何对…

CSS之布局(文档流)
文档流: <!DOCTYPE html> <html><head><meta charset"utf-8" /><title>文档流</title><style>.box1{background-color: yellow;}</style></head><body><!--文档流(normal fl…

网络管理员比赛回顾02-网关、静态路由、动态路由
目录 一、配置网关 二、配置静态路由 三、配置动态路由 3.1、使用RIP协议配置动态路由 3.2、使用OSPF协议配置动态路由 2021年9月参加青年网络管理员比赛,因为网管超龄不能按照“青年”参赛,临时培训我们这批“青年”参赛,回顾一下经过以…

[模拟]纺车的轮子 Spinning Wheels
题目链接 题目大意 5个轮子 每个轮子上面有w个缺口 缺口的初始角度是n 宽度是m 每秒转速v 求当他们同时开始转的情况下,什么时候他们的缺口足以让一道阳光通过(就是有重叠部分) 思考 纯模拟题目没啥说的,就是模拟轮子转1S 2S 3S .…

从头理解self-attention机制
注意力机制中较为重要的是self-attention机制,直接做了个小白能看懂的总结,也便于自己复习。 简介 self-attention机制就是想实现一连串的特征编码,两两之间的互相注意。有一串特征编码,x1, x2, …, xn,这里x1 x2 ……

筛选法求N以内的所有素数
素数:一个数只能被1和它本身整除的数。2是最小的素数#include <iostream> using namespace std; #define NUM 100 char isPrime[NUM 10]; int main() {//筛选法求素数//假设所有的素数都是素数,标志位设为1for(int i 2 ; i < NUM ; i){isPrim…

CSS之布局(盒模型)
盒模型: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>盒模型</title><style>.box1{/* 内容区(content),元素中的所有的子元素和文本内容都在内容区中排列内容区的大小由width和height两个属性来…
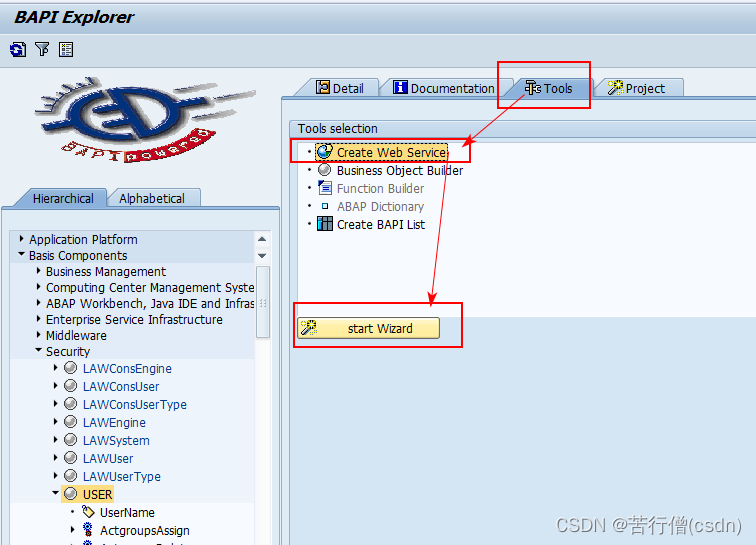
SAP创建webservice
目录 一、创建webservice 二、更改webservice 三、SoapUI测试webservice 四、查看webservice日志及排错 一、创建webservice 以用户相关的函数User为例创建webservice,事务码bapi查看bapi函数,BasisComponents-Security-User,选择Tools…

python面试题目
python面试题目 原文地址:https://www.usblog.cc/blog/post/justzhl/b5cc9a05c7d2 问题一:以下的代码的输出将是什么? 说出你的答案并解释。 ?1234567891011121314class Parent(object):x 1class Child1(Parent):passclass Child2(Parent):passprint …

vue2留言板
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>智能社——http://www.zhinengshe.com</title><meta name"viewport" content"widthdevice-width, initial-scale1.0, maximum…
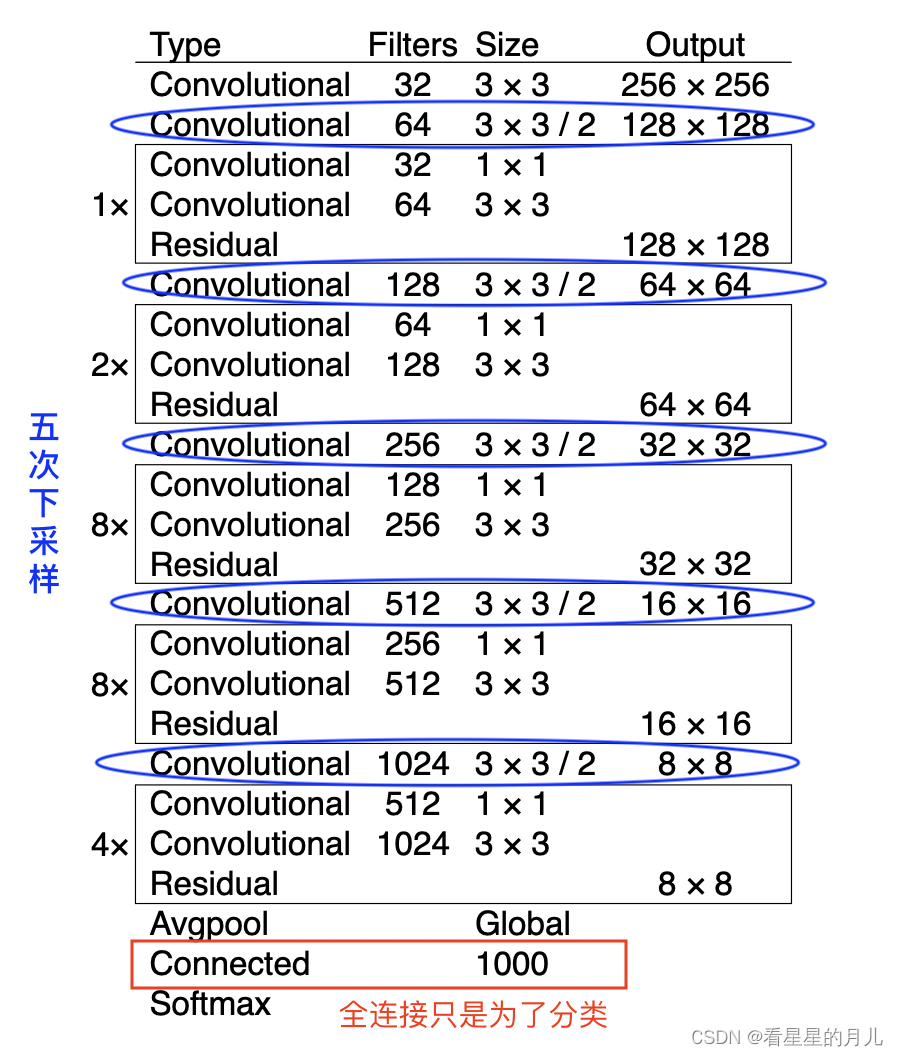
【目标检测】yolo系列:从yolov1到yolov5之YOLOv3详解及复现
在v1、v2的原理和技巧介绍之后,v3除了网络结构,其余的改变并不多。本文着重描述yolov3的原理细节。 相关阅读: 论文:YOLOv3: An Incremental Improvement 源码:https://github.com/ultralytics/yolov3 1. Yolov3网络…

CSS之布局(盒子模型—边框)
盒子模型—边框: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>盒子模型-边框</title><style>.box1{width: 200px;height: 200px;background-color: #bfa;/*border-width可以用来指定四个方向的…

SAP事务码f-02做账界面显示“页数”字段
事务码 f-02 做账界面,没有显示页数。 用户账号的参数添加 CSF (Country-Specific Fields)参数,参数值为 CN(伟大的China) 再次来到 f-02 的界面,显示了页数字段
