当前位置：首页 > 编程日记 > 正文

从头理解self-attention机制

编程日记 2024-06-08 05:40:00

注意力机制中较为重要的是self-attention机制，直接做了个小白能看懂的总结，也便于自己复习。

简介

self-attention机制就是想实现一连串的特征编码，两两之间的互相注意。有一串特征编码，x1, x2, …, xn，这里x1 x2 …都是一个特征向量，即让每个特征向量都关注到所有的特征向量（包括其自己），然后转变成一个更深层次的向量。

最原始的做法就是，两两之间作点积运算，然后生成一个n ✖️ n的矩阵，其中 i 行 j 列表示 xi 和 xj 之间的相似度。然后我们用这个相似度矩阵，再对 x 做加权平均，就得到一个y1, y2, …, yn，这个就是self-attention的输出。

举个简单的🌰，比如三个特征向量 x1 = [0.1, 0.5], x2 = [0.3, 0.4], x3 = [0.8, 0]，然后两两之间做点积运算，得到一个矩阵如下：
0.26 0.23 0.08
0.23 0.25 0.24
0.08 0.24 0.64
然后用这个矩阵对 x1, x2, x3 做加权平均，就是该权重矩阵的第 i 行单独拿出来，就是 yi 的加权值。计算方法就是：
y1 = 0.26 ✖️ x1 + 0.23 ✖️ x2 + 0.08 ✖️ x3
y2 = 0.23 ✖️ x1 + 0.25 ✖️ x2 + 0.24 ✖️ x3
y3 = 0.08 ✖️ x1 + 0.24 ✖️ x2 + 0.64 ✖️ x3

主要的操作

归一化

首先，加权值应当要归一化，即一行权重值加起来应该是1，否则 y 在数值上会变得不稳定（变得很大或者变得很小），所以权重矩阵要按行做归一化。归一化的方法就是Softmax，因为softmax更好求导，数值上相比于hard max也更稳定。

假设原先的计算方法是：Y = (X X^T) X
那么加入归一化后就是：Y = Softmax(X X^T) X

数值稳定

X X^T 这个权重矩阵也有问题，一般来说，一个特征向量中，每一个元素都是一个期望为0，方差为1的随机变量（为了数值稳定，特征向量每层都要做归一化，就是为了保证这个性质），我们希望后续运算过程中，所有的中间变量都可以保持期望为0，方差为1。

期望为0，方差为1的原因：假设方差很多，数值为出现很大的数字，比如100，这样求导的梯度也会变得很大，模型更新的幅度也会很大，就很不稳定了。甚至会出现梯度爆炸（就是更新的数值变成无穷大）或者梯度消失（更新数值为0，就是更新不动了）

但是点积运算会打破这一性质（所有的中间变量都可以保持期望为0，方差为1），例如，假设x1是一个64维的向量，x2也是个64维向量，两者点积后的结果，期望还是0，方差已经不是1了，方差变成了根号64=8。
见如下概率论公式：D(XY)=D(X)D(Y) - (E(X)E(Y))

d个随机变量相乘后相加，就是多个随机变量运算后的方差计算公式。应该除以根号d_k，才能把方差控制在1，d_k是特征向量的维度，所以公式就变成了：
Y = (X X^T / sqrt(d_k)) X

线性变换

这里运算都是X，太单一了，所以作者就让三个X分别做了三个线性变换，K、Q、V都是从 X 变换过来的线性变换的权重矩阵，根源都是同一个，所以其实就是自己跟自己做运算，分别是：
Q = W^Q X
K = W^K X
V = W^V X
这里线性变换就是nn.Linear(d_k, d_k)，不改变维度，只是做了一个线性投影。

把线性变换后的结果再去做attention运算：
Y = (Q K^T / sqrt(d_k)) V

一些总结

1. self-attention是线性运算吗？
答：不是。前面全是线性运算，非线性来自于归一化softmax。

2. self-attention的时间复杂度？
就看这个算法做了多少次原子运算。
例如：
两个向量点积，就是对应的元素乘起来然后累加（n次乘法+n次加法），复杂度是O(n)。
两个n✖️n矩阵相乘，结果有n✖️n个元素，每个元素是由n次乘法+n次加法得来的，所以时间复杂度是O(n^3).

所以，self-attention的时间复杂度如下：
1.每行归一化，一行softmax的时间复杂度是o(n)，那么n行就是o(n2)
2.往里面看，权重矩阵是看成一个矩阵乘法X X^T，X是nd_k维，所以是O(n✖️n✖️d)。过程：矩阵乘法，n✖️d d✖️n，结果n✖️n，每个元素d次
3.和V相乘，权重矩阵是n✖️n对吧，这个V是n✖️d，是O(n✖️n✖️d)。
所以，最后相加，总时间复杂度是O(n✖️n✖️d)。

3.根据公式写出代码

import numpy as np
import math
def self_attention(X):n, d = X.shape[:2]# 假设W_q  W_k  W_v是三个线性变换的权重矩阵W_q = np.random.rand(n * n)W_k = np.random.rand(n * n)W_v = np.random.rand(n * n)# 你来填 d个随机变量Q = np.matmul(W_q,X)K = np.matmul(W_k,X)V = np.matmul(W_v,X)W = np.matmul(Q,np.transpose(K))/math.sqrt(d)# -*- coding: utf-8 -*-def softmax(X):# reshape后面加个1就是为了让他可以跟x_exp相除# 比如说一个3 * 3的矩阵，可以跟3 * 1的矩阵相除的# 相除的时候，3 * 1的矩阵会扩展成3 * 3的，就是把列复制3份x_row_max = X.max(axis=1).reshape(list(X.shape)[:-1]+[1]) #按行找最大值X = X - x_row_max# 取最大值防溢出x_exp = np.exp(X)x_exp_row_sum = x_exp.sum(axis=1).reshape(list(X.shape)[:-1]+[1])softmax = x_exp / x_exp_row_sum #归一化return softmax# Y=softmax(Q K^T/sqrt(d))*VY = np.matmul(softmax(W),V)return Y

https://www.dkcj.cn/info/9769.html

从头理解self-attention机制

简介

主要的操作

归一化

数值稳定

线性变换

一些总结

相关文章：

筛选法求N以内的所有素数

CSS之布局（盒模型）

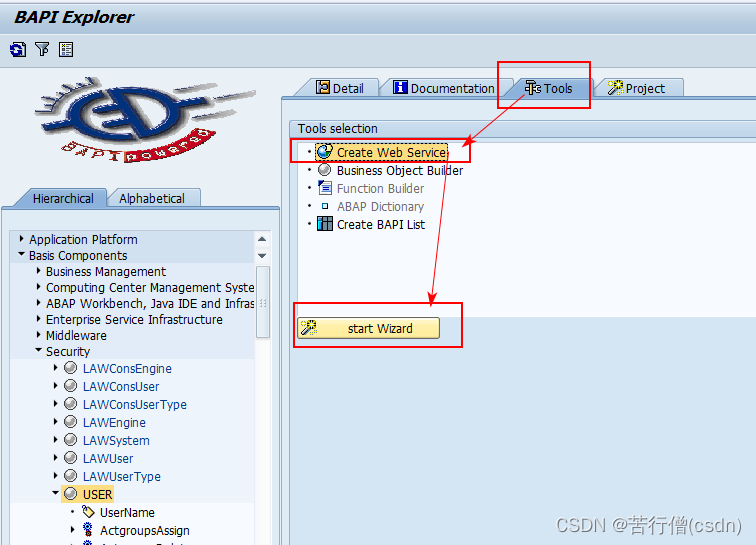
SAP创建webservice

python面试题目

vue2留言板

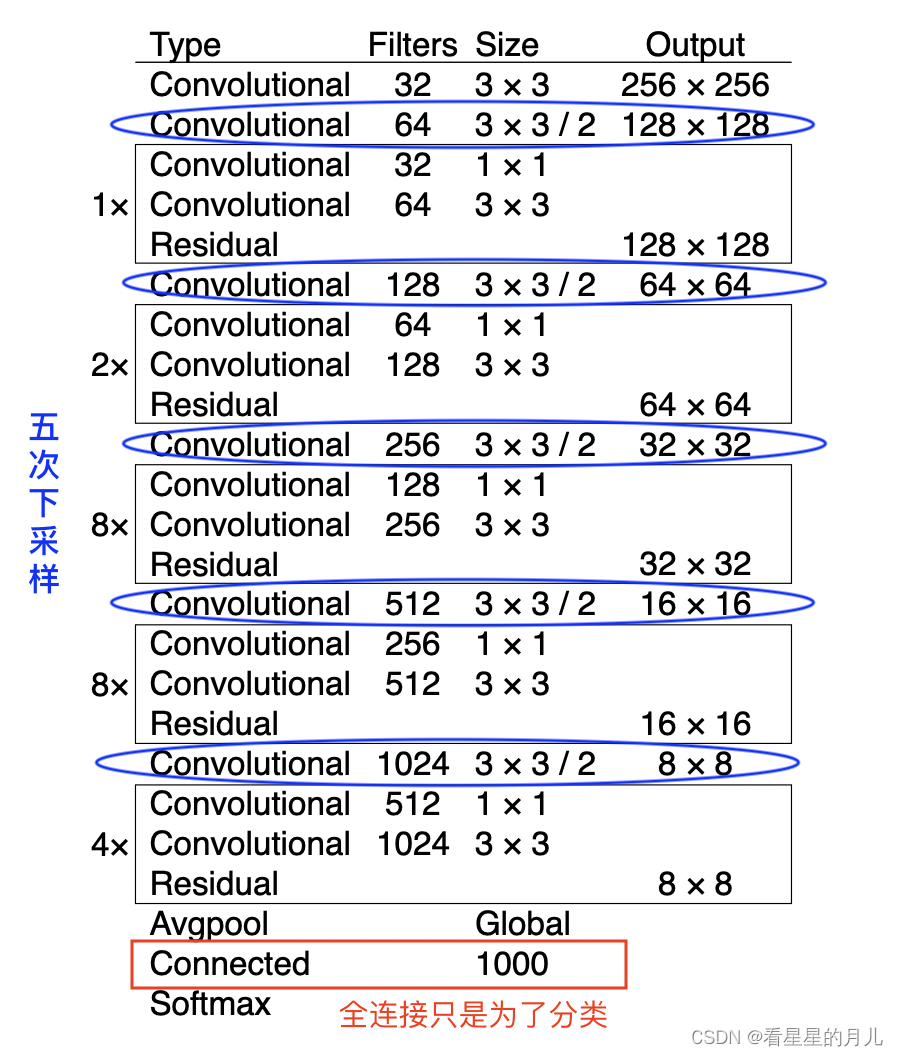
【目标检测】yolo系列：从yolov1到yolov5之YOLOv3详解及复现

CSS之布局（盒子模型—边框）

SAP事务码f-02做账界面显示“页数”字段

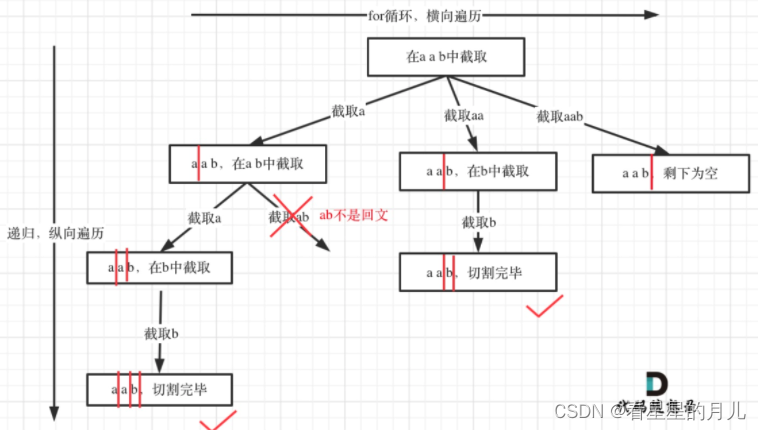
【Leetcode】刷题之路4（python版）

织梦文章内容屏蔽替换词语多个敏感字词

CSS之布局（盒子模型--内边距）

网络管理员比赛回顾04-DHCP

iOS-禁止scrollview垂直方向滚动，只允许水平方向滚动；或只允许垂直方向滚动...

go1.8之安装配置

栈和队列在python中的实现

CSS之布局（盒子模型--外边距）

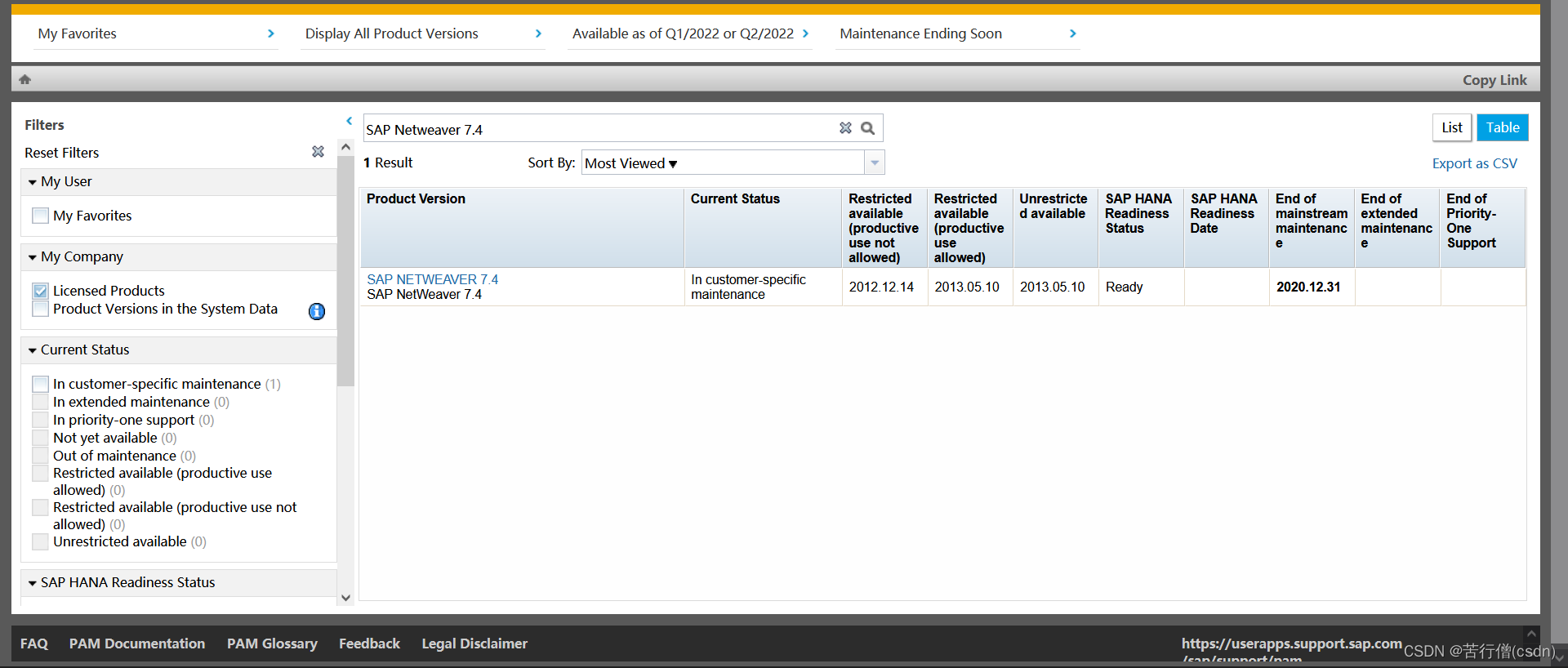
SAP Netweaver 7.4 SR2 Application Java Installation

Spring+SpringMVC+MyBatis深入学习及搭建(十)——MyBatis逆向工程

（一）七种AOP实现方法

[导入]Java线程的深入探讨

CSS之布局（盒子的水平布局）

IssueVission的命令处理

下一版本Windowsreg; CE 开发工具Smart Device Extensions for Microsoft Visual Studioreg; .NET...

vue 手机键盘把底部按钮顶上去

CSS之布局（盒子的垂直布局）

microsoft 为microbit.org 设计的课程

Java, Mono, or C++?

CSS之布局（外边距的折叠）

图论--欧拉路，欧拉回路(小结)

轻松一下，看看vs.net2002变态的智能提示，不知道算不算bug