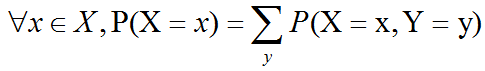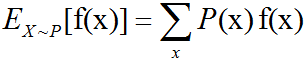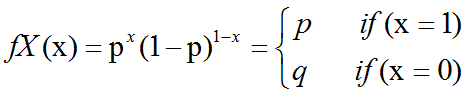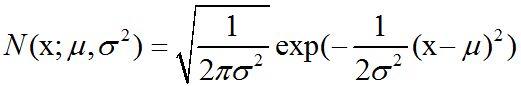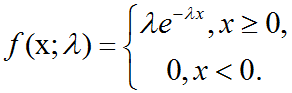开发四年只会写业务代码,分布式高并发都不会还做程序员? 
新增
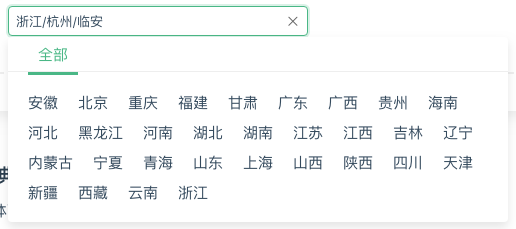
CategoryPicker
新增组件 CategoryPicker,地址级联组件的最佳方案。
<CategoryPicker :option="option" v-model="value"/>
相关文档
ImagePreview
新增组件 ImagePreview,图片预览列表。
<ImagePreview :datas="datas" @click="openPreview"/>

相关文档
Modal
modal 支持自定义事件替换event事件,并支持多参数传递。
// 直接使用emit触发外部的events监听,兼容性 1.18.0+
this.$emit('success', this.value, 'test');相关文档
Pagination
支持 v-model 分页控制。
<Pagination v-model="pagination" @change="getData"></Pagination>pagination: {page: 1,size: 10,total: 100
}
相关文档
Tree
新增 expand 方法,可以通过 key 指定打开哪些节点。
this.$refs.tree.expand([1,2,3]);
相关文档
Button
新增属性 transparent ,按钮是否背景透明。
<Button transparent text-color="primary">主色系按钮</Button>
相关文档
TimelineItem
新增slot icon
<TimelineItem><i class="h-icon-user primary-color" slot="icon"></i><div slot="time">2012-12-23</div><div slot="content">到达呼伦贝尔</div> </TimelineItem>
相关文档
FormItem
新增属性 icon ,显示图标。
<FormItem label="密码" icon="h-icon-complete" prop="password"><input type="password" v-model="model.password"> </FormItem>
新增 slot label,自定义slot。
<FormItem label="用户名" prop="name"><template v-slot:label><i class="h-icon-user"></i> 用户名</template><input type="text" v-model="model.name"> </FormItem>

相关文档
Tooltip
新增属性 editable,支持tooltip内部编辑模块
<Tooltip theme="white" @show="show" trigger="click" @hide="hide" editable><span class="text-hover">Component调用</span><div slot="content"><div v-padding="10"><Select dict="simple" v-model="value" style="width: 200px;"></Select></div></div> </Tooltip>
相关文档
Category
补充异步加载功能
<Category :option="param" v-model="value"></Category>param: {keyName: 'id',titleName: 'title',dataMode: 'list',getDatas: (parent, resolve) => {setTimeout(() => {if (!parent) {resolve([{ id: 1, title: '一级', disabled: true },{ id: 2, title: '二级' },{ id: 3, title: '三级' }]);} else if (parent.id % 2 == 0) {resolve([]);} else {resolve(genList(parent.title, parent.id, 5, 'id', 'title'));}}, 100);}
}相关文档
修复bug
日期时间选择器选择问题
选择日期时间后,不关闭,直接重新选择年月无效。
超级日期选择器,点下一页稍微快一点,就会变成选中状态
Closes #91
栅格布局错位问题
Closes #90