计算机解决问题没有奇技淫巧,但动态规划还是有点套路

【导读】动态规划算法似乎是一种很高深莫测的算法,你会在一些面试或算法书籍的高级技巧部分看到相关内容,什么状态转移方程,重叠子问题,最优子结构等高大上的词汇也可能让你望而却步。
而且,当你去看用动态规划解决某个问题的代码时,你会觉得这样解决问题竟然如此巧妙,但却难以理解,你可能惊讶于人家是怎么想到这种解法的。
实际上,动态规划是一种常见的「算法设计技巧」,并没有什么高深莫测,至于各种高大上的术语,那是吓唬别人用的,只要你亲自体验几把,这些名词的含义其实显而易见,再简单不过了。
至于为什么最终的解法看起来如此精妙,是因为动态规划遵循一套固定的流程:递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法。这个过程是层层递进的解决问题的过程,你如果没有前面的铺垫,直接看最终的非递归动态规划解法,当然会觉得牛逼而不可及了。
当然,见的多了,思考多了,是可以一步写出非递归的动态规划解法的。任何技巧都需要练习,我们先遵循这个流程走,算法设计也就这些套路,除此之外,真的没啥高深的。
以下,先通过两个个比较简单的例子:斐波那契和凑零钱问题,揭开动态规划的神秘面纱,描述上述三个流程。后续还会写几篇文章探讨如何使用动态规划技巧解决比较复杂的经典问题。
首先,第一个快被举烂了的例子,斐波那契数列。请读者不要嫌弃这个例子简单,因为简单的例子才能让你把精力充分集中在算法背后的通用思想和技巧上,而不会被那些隐晦的细节问题搞的莫名其妙。后续,困难的例子有的是。
PS:但凡遇到需要递归的问题,最好都画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨大帮助。
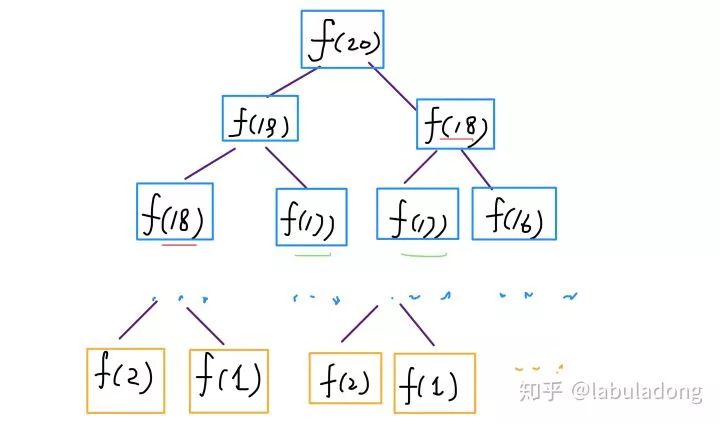
这个递归树怎么理解?就是说想要计算原问题 f(20),我就得先计算出子问题 f(19) 和 f(18),然后要计算 f(19),我就要先算出子问题 f(18) 和 f(17),以此类推。最后遇到 f(1) 或者 f(2) 的时候,结果已知,就能直接返回结果,递归树不再向下生长了。
递归算法的时间复杂度怎么计算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
解决一个子问题的时间,在本算法中,没有循环,只有 f(n - 1) + f(n - 2) 一个加法操作,时间为 O(1)。
所以,这个算法的时间复杂度为 O(2^n),指数级别,爆炸。
观察递归树,很明显发现了算法低效的原因:存在大量重复计算,比如 f(18) 被计算了两次,而且你可以看到,以 f(18) 为根的这个递归树体量巨大,多算一遍,会耗费巨大的时间。更何况,还不止 f(18) 这一个节点被重复计算,所以这个算法及其低效。
这就是动态规划问题的第一个性质:重叠子问题。下面,我们想办法解决这个问题。
步骤二、带备忘录的递归解法
明确了问题,其实就已经把问题解决了一半。即然耗时的原因是重复计算,那么我们可以造一个「备忘录」,每次算出某个子问题的答案后别急着返回,先记到「备忘录」里再返回;每次遇到一个子问题先去「备忘录」里查一查,如果发现之前已经解决过这个问题了,直接把答案拿出来用,不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
现在,画出递归树,你就知道「备忘录」到底做了什么。
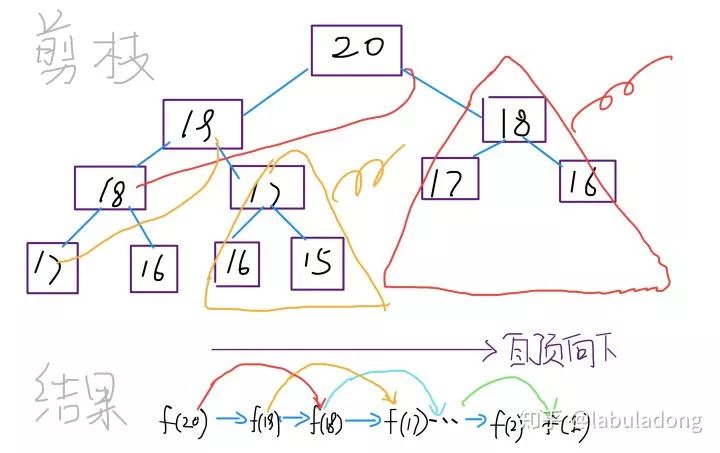
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
递归算法的时间复杂度怎么算?子问题个数乘以解决一个子问题需要的时间。
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 f(1), f(2), f(3) ... f(20),数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
至此,带备忘录的递归解法的效率已经和动态规划一样了。实际上,这种解法和动态规划的思想已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
啥叫「自顶向下」?注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解规模,直到 f(1) 和 f(2) 触底,然后逐层返回答案,这就叫「自顶向下」。
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
步骤三、动态规划
有了上一步「备忘录」的启发,我们可以把这个「备忘录」独立出来成为一张表,就叫做 DP table 吧,在这张表上完成「自底向上」的推算岂不美哉!
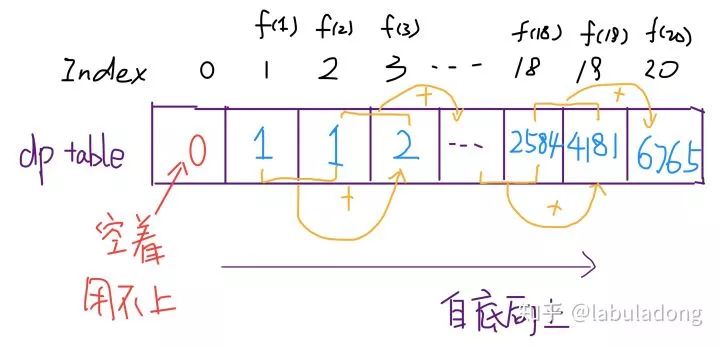
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已。实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
这里,引出「动态转移方程」这个名词,实际上就是描述问题结构的数学形式:
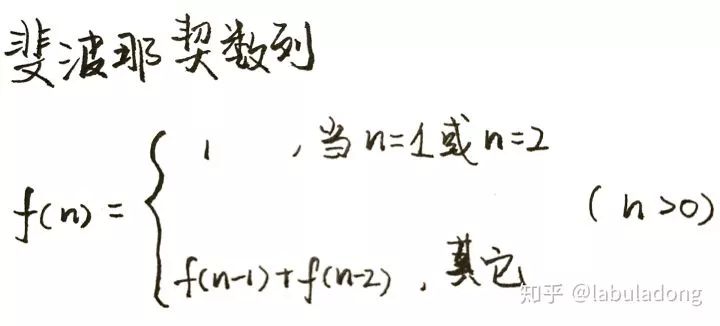
为啥叫「状态转移方程」?为了听起来高端。你把 f(n) 想做一个状态 n,这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来,这就叫状态转移,仅此而已。
你会发现,上面的几种解法中的所有操作,例如 return f(n - 1) + f(n - 2),dp[i] = dp[i - 1] + dp[i - 2],以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性,它是解决问题的核心。很容易发现,其实状态转移方程直接代表着暴力解法。
千万不要看不起暴力解,动态规划问题最困难的就是写出状态转移方程,即这个暴力解。优化方法无非是用备忘录或者 DP table,再无奥妙可言。
这个例子的最后,讲一个细节优化。细心的读者会发现,根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了。所以,可以进一步优化,把空间复杂度降为 O(1):
有人会问,动态规划的另一个重要特性「最优子结构」,怎么没有涉及?下面会涉及。斐波那契数列的例子严格来说不算动态规划,以上旨在演示算法设计螺旋上升的过程。当问题中要求求一个最优解或在代码中看到循环和 max、min 等函数时,十有八九,需要动态规划大显身手。
下面,看第二个例子,凑零钱问题,有了上面的详细铺垫,这个问题会很快解决。
题目:给你 k 种面值的硬币,面值分别为 c1, c2 ... ck,再给一个总金额 n,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,则回答 -1 。
比如说,k = 3,面值分别为 1,2,5,总金额 n = 11,那么最少需要 3 枚硬币,即 11 = 5 + 5 + 1 。下面走流程。
一、暴力解法
\首先是最困难的一步,写出状态转移方程,这个问题比较好写:

其实,这个方程就用到了「最优子结构」性质:原问题的解由子问题的最优解构成。即 f(11) 由 f(10), f(9), f(6) 的最优解转移而来。
记住,要符合「最优子结构」,子问题间必须互相独立。啥叫相互独立?你肯定不想看数学证明,我用一个直观的例子来讲解。
比如说,你的原问题是考出最高的总成绩,那么你的子问题就是要把语文考到最高,数学考到最高...... 为了每门课考到最高,你要把每门课相应的选择题分数拿到最高,填空题分数拿到最高...... 当然,最终就是你每门课都是满分,这就是最高的总成绩。
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,“每门科目考到最高”这些子问题是互相独立,互不干扰的。
但是,如果加一个条件:你的语文成绩和数学成绩会互相制约,此消彼长。这样的话,显然你能考到的最高总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为子问题并不独立,语文数学成绩无法同时最优,所以最优子结构被破坏。
回到凑零钱问题,显然子问题之间没有相互制约,而是互相独立的。所以这个状态转移方程是可以得到正确答案的。
之后就没啥难点了,按照方程写暴力递归算法即可。
画出递归树:
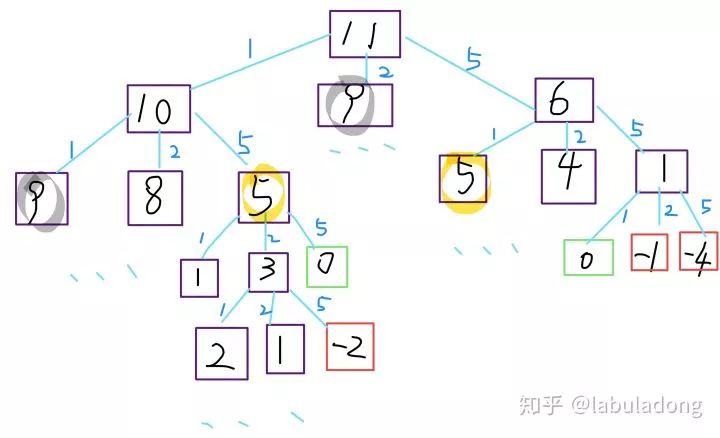
时间复杂度分析:子问题总数 x 每个子问题的时间。子问题总数为递归树节点个数,这个比较难看出来,是 O(n^k),总之是指数级别的。每个子问题中含有一个 for 循环,复杂度为 O(k)。所以总时间复杂度为 O(k*n^k),指数级别。
二、带备忘录的递归算法
不画图了,很显然「备忘录」大大减小了子问题数目,完全消除了子问题的冗余,所以子问题总数不会超过金额数 n,即子问题数目为 O(n)。处理一个子问题的时间不变,仍是 O(k),所以总的时间复杂度是 O(kn)。
三、动态规划
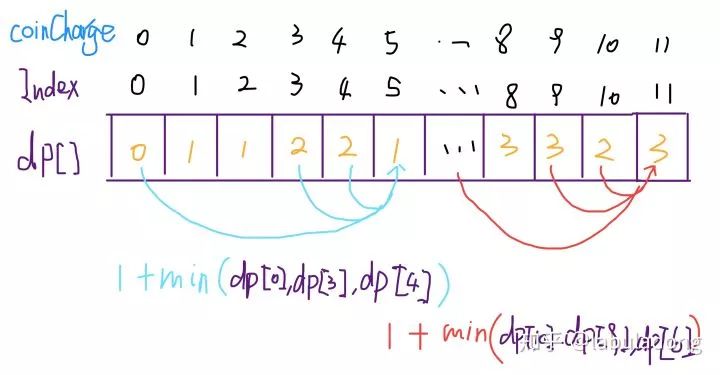
最后总结
如果你不太了解动态规划,还能看到这里,真得给你鼓掌,相信你已经掌握了这个算法的设计技巧。
计算机解决问题其实没有任何奇技淫巧,它唯一的解决办法就是穷举,穷举所有可能性。算法设计无非就是先思考“如何穷举”,然后再追求“如何聪明地穷举”。
列出动态转移方程,就是在解决“如何穷举”的问题。之所以说它难,一是因为很多穷举需要递归实现,二是因为有的问题本身的解空间复杂,不那么容易穷举完整。
备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路,是降低时间复杂度的不二法门,除此之外,试问,还能玩出啥花活?
◆
精彩推荐
◆
2019 中国大数据技术大会(BDTC)历经十一载,再度火热来袭!豪华主席阵容及百位技术专家齐聚,15 场精选专题技术和行业论坛,超强干货+技术剖析+行业实践立体解读,深入解析热门技术在行业中的实践落地。【早鸟票】与【特惠学生票】限时抢购,扫码了解详情!

推荐阅读
阿里披露AI完整布局,飞天AI平台首次亮相解决掉这些痛点和难点,让知识图谱不再是“噱头”
Python数据分析实战基础 | 清洗常用4板斧
一行代码弄懂数据,Pandas最佳搭档就是ta了
如何理解 Python 中的面向对象编程?
6张拓扑图揭秘中心化交易所的5种行为, 原来中心化比你想象的重要
TDD 就是个坑
厉害!接班马云的为何是张勇?

你点的每个“在看”,我都认真当成了喜欢
相关文章:

idea下,Jetty采用main方法启动web项目
为什么80%的码农都做不了架构师?>>> 对于maven多模块的spring web项目,本地开发时,启动的方式一般有如下几种: 使用容器(tomcat/jetty/resin等),该方式需要ide支持,而社…
概率论中均值、方差、标准差介绍及C++/OpenCV/Eigen的三种实现
概率论是用于表示不确定性声明(statement)的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性声明的公理。在人工智能领域,概率论主要有两种用途。首先,概率法则告诉我们AI系统如何推理,据此我们设计一些算…

[转]CentOS 5.5下FTP安装及配置
一、FTP的安装 1、检测是否安装了FTP : [rootlocalhost ~]# rpm -q vsftpd vsftpd-2.0.5-16.el5_5.1 否则显示:[rootlocalhost ~]# package vsftpd is not installed 查看ftp运行状态 service vsftpd status 2、如果没安装FTP,运行yum install vsftpd命令进行安装 如…

C++11中头文件thread的使用
C11中加入了<thread>头文件,此头文件主要声明了std::thread线程类。C11的标准类std::thread对线程进行了封装。std::thread代表了一个线程对象。应用C11中的std::thread便于多线程程序的移值。 <thread>是C标准程序库中的一个头文件,定义了…

python3 urllib 类
urllib模块中的方法 1.urllib.urlopen(url[,data[,proxies]]) 打开一个url的方法,返回一个文件对象,然后可以进行类似文件对象的操作。本例试着打开google >>> import urllib >>> f urllib.urlopen(http://www.google.com.hk/) >&…
阿里飞天大数据飞天AI平台“双生”系统正式发布,9大全新数据产品集中亮相
作者 | 夕颜 责编 | 唐小引 出品 | AI科技大本营(ID:rgznai100) 如今,大数据和 AI 已经成为两个分不开的词汇,没有大数据,AI 就失去了根基;没有 AI,数据不会呈现爆发式的增长。如何将 AI 与大…

关于JavaScript的闭包(closure)
(转载自阮一峰博客) 闭包(closure)是Javascript语言的一个难点,也是它的特色,更是函数式编程的重要思想之一,很多高级应用都要依靠闭包实现。 下面就是我的学习笔记,对于Javascript初…
Vagrant控制管理器——“Hobo”
Hobo是控制Vagrant盒子和在Mac上编辑Vagrantfiles的最佳和最简单的方法。您可以快速启动,停止和重新加载您的Vagrant机器。您可以从头开始轻松创建新的Vagrantfile。点击进入,尽享Hobo for Mac全部功能! Hobo做什么? 启动…

微众银行AI团队开源联邦学习框架,并发布《联邦学习白皮书1.0》
(图片由AI科技大本营付费下载自视觉中国)编辑 | Jane来源 | 《联邦学习白皮书1.0》出品 | AI科技大本营(ID:rgznai100)【导语】2019年,联邦学习成为业界技术研究与应用的焦点。近日,微众银行 AI 项目组编制…

C++11中头文件atomic的使用
原子库为细粒度的原子操作提供组件,允许无锁并发编程。涉及同一对象的每个原子操作,相对于任何其他原子操作是不可分的。原子对象不具有数据竞争(data race)。原子类型对象的主要特点就是从不同线程访问不会导致数据竞争。因此从不同线程访问某个原子对象…

Oracle回收站
回收站是删除对象使用的存储空间。可以使用实例参数recyclebin禁用回收站,默认是on,可以为某个会话或系统设置为off或on。所有模式都有一个回收站。 当表空间不足时可以自动重用回收站对象占用的表空间(此后不可能恢复对象)&#…
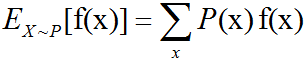
协方差矩阵介绍及C++/OpenCV/Eigen的三种实现
函数f(x)关于某分布P(x)的期望(expectation)或者期望值(expected value)是指,当x由P产生,f作用于x时,f(x)的平均值。对于离散型随机变量,这可以通过求和得到:对于连续型随机变量可以通过求积分得到:当概率分…
10分钟搭建你的第一个图像识别模型 | 附完整代码
(图片由AI科技大本营付费下载自视觉中国)作者 | Pulkit Sharma译者 | 王威力来源 | 数据派THU(ID:DatapiTHU)【导读】本文介绍了图像识别的深度学习模型的建立过程,通过陈述实际比赛的问题、介绍模型框架和…

Rancher 2.2.2 发布,优化 Kubernetes 集群运维
开发四年只会写业务代码,分布式高并发都不会还做程序员? >>> Rancher 2.2.2 发布了。Rancher 是一个开源的企业级 Kubernetes 平台,可以管理所有云上、所有发行版、所有 Kubernetes集群,解决了生产环境中企业用户可能面…

EXP/EXPDP, IMP/IMPDP应用
2019独角兽企业重金招聘Python工程师标准>>> EXP/EXPDP, IMP/IMPDP应用 exp name/pwddbname filefilename.dmp tablestablename rowsy indexesn triggersn grantsn $ sqlplus username/passwordhostname:port/SERVICENAME OR $ sqlplus username Enter password:…

微软语音AI技术与微软听听文档小程序实践 | AI ProCon 2019
演讲嘉宾 | 赵晟、张鹏整理 | 伍杏玲来源 | CSDN(ID:CSDNnews)【导语】9 月 7 日,在CSDN主办的「AI ProCon 2019」上,微软(亚洲)互联网工程院人工智能语音团队首席研发总监赵晟、微软࿰…

C++11中std::condition_variable的使用
<condition_variable>是C标准程序库中的一个头文件,定义了C11标准中的一些用于并发编程时表示条件变量的类与方法等。条件变量是并发程序设计中的一种控制结构。多个线程访问一个共享资源(或称临界区)时,不但需要用互斥锁实现独享访问以避免并发错…

docker基础文档(链接,下载,安装)
一、docker相关链接1.docker中国区官网(包含部分中文文档,下载安装包,镜像加速器):https://www.docker-cn.com/2.docker官方镜像仓库:https://cloud.docker.com/3.docker下载:https://www.docker-cn.com/community-edi…

一个JS对话框,可以显示其它页面,
还不能自适应大小 garyBox.js // JavaScript Document// gary 2014-3-27// 加了 px 在google浏览器没加这个发现设置width 和height没有用 //gary 2014-3-27 //实在不会用那些JS框架,自己弄个,我只是想要个可以加载其它页面的对话框而以,这里用了别人的…

只需4秒,这个算法就能鉴别你的LV是真是假
(图片付费下载自视觉中国)导语:假冒奢侈品制造这个屡禁不止的灰色产业,每年给正品商家和消费者造成上千亿的损失,对企业和消费者造成伤害。作为全球奢侈品巨头,LVMH 对假冒奢侈品的打击十分重视。LVMH 其旗…
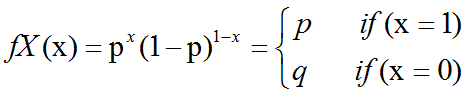
概率论中伯努利分布(bernoulli distribution)介绍及C++11中std::bernoulli_distribution的使用
Bernoulli分布(Bernoulli distribution):是单个二值随机变量的分布。它由单个参数∈[0,1],给出了随机变量等于1的概率。它具有如下的一些性质:P(x1) P(x0)1-P(xx) x(1-)1-xEx[x] Varx(x) (1-)伯努力分布(Bernoulli distribution,又…

关于View测量中的onMeasure函数
在自定义View中我们通常会重写onMeasure,下面来说说这个onMeasure有什么作用 onMeasure主要用于对于View绘制时进行测量 Override protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {super.onMeasure(widthMeasureSpec, heightMeasureSpec);…

zabbix二次开发之从mysql取值在运维平台js图表展现
前沿:集群控制平台已经要慢慢的灰度上线了,出问题的时候,才找点bug,时间有点空闲。正好看了下zabbix的数据库,产生了自己想做一套能更好的展现zabbix的页面。更多内容请到我的个人的博客站点,blog.xiaorui.…
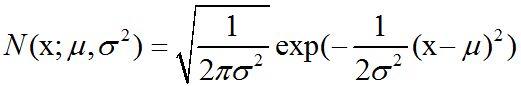
概率论中高斯分布(正态分布)介绍及C++11中std::normal_distribution的使用
高斯分布:最常用的分布是正态分布(normal distribution),也称为高斯分布(Gaussian distribution):正态分布N(x;μ,σ2)呈现经典的”钟形曲线”的形状,其中中心峰的x坐标由μ给出,峰的宽度受σ控制。正态分布由两个参数…

AI落地遭“卡脖子”困境:为什么说联邦学习是解决良方?
作者 | Just出品 | AI科技大本营(ID:rgznai100)毋庸置疑,在业界对人工智能(AI)应用落地备受期待的时期,数据这一重要支点却越来越成为一个“卡脖子”的难题。AI落地需要数据来优化模型效果,但大…

Linux下截取指定时间段日志并输出到指定文件
sed -n /2019-04-22 16:10:/,/2019-04-22 16:20:/p log.log > bbb.txt 转载于:https://www.cnblogs.com/mrwuzs/p/10752037.html

nginx+keepalive主从双机热备+自动切换解决方案
环境采集cenots 6.3 64位迷你安装,因为安装前,你需要做一些工作yum install -y make wget如果你愿意可以更新下系统,更换下yum源.1.安装keepalive官方最新版 keepalived-1.2.7tar zxvf keepalived-1.2.7.tar.gzcd keepalived-1.2.7在此之前。…
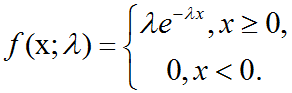
概率论中指数分布介绍及C++11中std::exponential_distribution的使用
指数分布:在深度学习中,我们经常会需要一个在x0点处取得边界点(sharp point)的分布。为了实现这一目的,我们可以使用指数分布(exponential distribution): p(x;λ) λlx≥0exp(-λx)指数分布使用指示函数(indicator function) lx≥…
肖仰华:知识图谱构建的三要素、三原则和九大策略 | AI ProCon 2019
演讲嘉宾 | 肖仰华(复旦大学教授、博士生导师,知识工场实验室负责人) 编辑 | Jane 出品 | AI科技大本营(ID:rgznai100) 近两年,知识图谱技术得到了各行各业的关注,无论是企业公司还…

Docker mongo副本集环境搭建
1、MongoDB Docker 镜像安装 docker pull mongo 2、Docker容器创建 MongoDB Docker 容器创建有以下几个问题: 1- MongoDB 容器基本创建方法和数据目录挂载 2- MongoDB 容器的数据迁移 3- MongoDB 设置登录权限问题docker run -p 27017:27017 -v <LocalDirectoryP…
