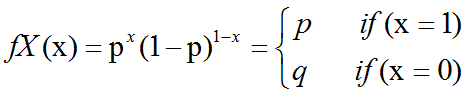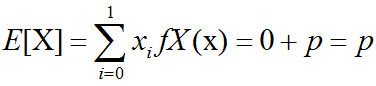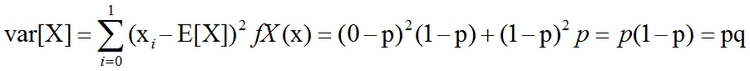概率论中伯努利分布(bernoulli distribution)介绍及C++11中std::bernoulli_distribution的使用
Bernoulli分布(Bernoulli distribution):是单个二值随机变量的分布。它由单个参数ø∈[0,1],ø给出了随机变量等于1的概率。它具有如下的一些性质:
P(x=1)= ø
P(x=0)=1-ø
P(x=x)= øx(1-ø)1-x
Ex[x]= ø
Varx(x)= ø(1-ø)
伯努力分布(Bernoulli distribution,又名两点分布或者0-1分布)是一个离散型概率分布,为纪念瑞士科学家雅各布·伯努利而命名。若伯努利试验成功,则伯努利随机变量取值为1。若伯努利试验失败,则伯努利随机变量取值为0。记其成功概率为p(0≤p≤1),失败概率为q=1-p。则:
其概率质量函数为:
其期望值为:
其方差为:
Multinoulli分布(multionoulli distribution)或者范畴分布(categorical distribution):是指在具有k个不同状态的单个离
散型随机变量上的分布,其中k是一个有限值。Multinoulli分布由向量p∈[0,1]k-1参数化,其中每一个分量pi表示第i个状
态的概率。最后的k个状态的概率可以通过1-lTp给出。注意必须限制lTp≤1。Multinoulli分布经常用来表示对象分类的分
布,所以很少假设状态1具有数值1之类的。因此,我们通常不需要去计算Multinoulli分布的随机变量的期望和方差.
Bernoulli分布和Multinoulli分布足够用来描述在它们领域内的任意分布。它们能够描述这些分布,不是因为它们
特别强大,而是因为它们的领域很简单;它们可以对那些能够将所有的状态进行枚举的离散型随机变量进行建模。
当处理的是连续型随机变量时,会有不可数无限多的状态,所以任何通过少量参数描述的概率分布都必须在分布上加以
严格的控制。
“multinoulli”这个术语是最近被Gustavo Lacerdo发明,被Murphy(2012)推广的。Multinoulli分布是多项式分
布(multinomial distribution)的一个特例。多项式分布是{0,…,n}k中的向量的分布,用于表示当对Multinoulli分布采
样n次时k个类中的每一个被访问的次数。多项式分布(multinomial distribution)是二项式分布的推广。二项分布的
典型例子是扔硬币,硬币正面朝上概率为p,重复扔n次硬币,k次为正面的概率即为一个二项式分布概率。把二
项分布推广至多个(大于2)互斥事件的发生次数,就得到了多项式分布。比如扔骰子,不同于扔硬币,骰子有6个
面对应6个不同的点数,这样单次每个点数朝上的概率都是1/6.
In probability theory and statistics, a categorical distribution(分类分布)(also called a generalized Bernoulli
distribution(广义伯努利分布), multinoull distribution or, less precisely, a discrete distribution) is a probabilit
distribution that describes the possible results of a random event that can take on one of K possible outcomes,
with the probability of each outcom separately specified. There is not necessarily an underlying ordering of thes
outcomes, but numerical labels are often attached for convenience in describing the distribution. On the other
hand, the categorical distribution is a special case of the multinomial distribution.
以上内容摘自:《深度学习中文版》和 维基百科
以下是对C++11中伯努利分布std::bernoulli_distribution类介绍:
C++11在头文件<random>中提供了伯努利概率分布类std::Bernoulli_distribution。伯努利分布(Bernoulli distribution)是判断某件事情发生或者未发生的概率,产生随机bool值。它是一个单次试验只有0(失败)和1(成功)两个结果的离散分布。
std::bernoulli_distribution:Bernoulli distribution, Random number distribution that produces bool values according to a Bernoulli distribution.#include "bernoulli_distribution.hpp"
#include <iostream>
#include <random>
#include <string>
#include <iomanip>
#include <map>/
// reference: http://www.cplusplus.com/reference/random/bernoulli_distribution/
int test_bernoulli_distribution_1()
{
{const int nrolls = 10000;std::default_random_engine generator;std::bernoulli_distribution distribution(0.5);int count = 0; // count number of truesfor (int i = 0; i<nrolls; ++i) if (distribution(generator)) ++count;std::cout << "bernoulli_distribution (0.5) x 10000:" << std::endl;std::cout << "true: " << count << std::endl;std::cout << "false: " << nrolls - count << std::endl;
}{ // (1)、bernoulli_distribution::bernoulli_distribution: Constructs a bernoulli_distribution object
// with a probability of p (or with the probability specified by object parm)
// (2)、bernoulli_distribution::operator(): Generate random number
// Returns a new random value with the probability associated to the object (version 1) or
// with the probability specified by parm (version 2)
// (3)、bernoulli_distribution::p: Probability of true
// Returns the parameter p associated with the bernoulli_distribution.
// This parameter represents the probabily that member function operator() returns true.
// (4)、bernoulli_distribution::max:Maximum value, Returns the least upper bound of the range of
// values potentially returned by member operator(), which for bernoulli_distribution is true.
// (5)、bernoulli_distribution::min: Minimum value, Returns the greatest lower bound of the range of
// values potentially returned by member operator(), which for bernoulli_distribution is false.std::cout << "Please, enter a yes/no question (I will answer it):" << std::endl;std::string text;getline(std::cin, text);std::seed_seq seed(text.begin(), text.end()); // seed using questionstd::default_random_engine generator(seed);std::bernoulli_distribution distribution(0.91);bool result = distribution(generator);std::cout << (result ? "yes" : "no") << std::endl;std::cout << "p: " << distribution.p() << std::endl;std::cout << "max: " << distribution.max() << std::endl;std::cout << "min: " << distribution.min() << std::endl;
}{ // bernoulli_distribution::param: Distribution parameters
// A bernoulli_distribution is defined by a single parameter: its probability (p) of true results.
// An object of type param_type carries this information, but it is meant to be used only to construct
// or specify the parameters for a bernoulli_distribution object, not to inspect the individual parameter.std::default_random_engine generator;std::bernoulli_distribution d1(0.7);std::bernoulli_distribution d2(d1.param());// print two independent values:std::cout << std::boolalpha;std::cout << d1(generator) << std::endl;std::cout << d2(generator) << std::endl;
}{ // bernoulli_distribution::reset: Resets the distribution,
// so that subsequent uses of the object do not depend on values already produced by it.std::default_random_engine generator;std::bernoulli_distribution distribution;// print two independent values:std::cout << std::boolalpha;std::cout << distribution(generator) << std::endl;distribution.reset();std::cout << distribution(generator) << std::endl;
}return 0;
}/
// reference: http://en.cppreference.com/w/cpp/numeric/random/bernoulli_distribution
int test_bernoulli_distribution_2()
{std::random_device rd;std::mt19937 gen(rd());// give "true" 1/4 of the time// give "false" 3/4 of the timestd::bernoulli_distribution d(0.25);std::map<bool, int> hist;for (int n = 0; n<10000; ++n) {++hist[d(gen)];}for (auto p : hist) {std::cout << std::boolalpha << std::setw(5) << p.first<< ' ' << std::string(p.second / 500, '*') << '\n';}return 0;
}/
int test_bernoulli_distribution_3()
{std::random_device rd; std::mt19937 gen(rd()); // 每次产生不固定的不同的值//std::default_random_engine gen; // 每次产生固定的不同的值std::bernoulli_distribution d(0.5);for (int i = 0; i < 10; ++i)std::cout << d(gen);std::cout << std::endl;return 0;
}GitHub: https://github.com/fengbingchun/Messy_Test
相关文章:

关于View测量中的onMeasure函数
在自定义View中我们通常会重写onMeasure,下面来说说这个onMeasure有什么作用 onMeasure主要用于对于View绘制时进行测量 Override protected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {super.onMeasure(widthMeasureSpec, heightMeasureSpec);…

zabbix二次开发之从mysql取值在运维平台js图表展现
前沿:集群控制平台已经要慢慢的灰度上线了,出问题的时候,才找点bug,时间有点空闲。正好看了下zabbix的数据库,产生了自己想做一套能更好的展现zabbix的页面。更多内容请到我的个人的博客站点,blog.xiaorui.…
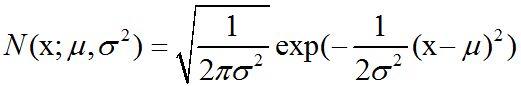
概率论中高斯分布(正态分布)介绍及C++11中std::normal_distribution的使用
高斯分布:最常用的分布是正态分布(normal distribution),也称为高斯分布(Gaussian distribution):正态分布N(x;μ,σ2)呈现经典的”钟形曲线”的形状,其中中心峰的x坐标由μ给出,峰的宽度受σ控制。正态分布由两个参数…

AI落地遭“卡脖子”困境:为什么说联邦学习是解决良方?
作者 | Just出品 | AI科技大本营(ID:rgznai100)毋庸置疑,在业界对人工智能(AI)应用落地备受期待的时期,数据这一重要支点却越来越成为一个“卡脖子”的难题。AI落地需要数据来优化模型效果,但大…

Linux下截取指定时间段日志并输出到指定文件
sed -n /2019-04-22 16:10:/,/2019-04-22 16:20:/p log.log > bbb.txt 转载于:https://www.cnblogs.com/mrwuzs/p/10752037.html

nginx+keepalive主从双机热备+自动切换解决方案
环境采集cenots 6.3 64位迷你安装,因为安装前,你需要做一些工作yum install -y make wget如果你愿意可以更新下系统,更换下yum源.1.安装keepalive官方最新版 keepalived-1.2.7tar zxvf keepalived-1.2.7.tar.gzcd keepalived-1.2.7在此之前。…
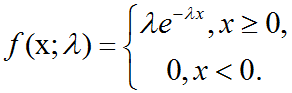
概率论中指数分布介绍及C++11中std::exponential_distribution的使用
指数分布:在深度学习中,我们经常会需要一个在x0点处取得边界点(sharp point)的分布。为了实现这一目的,我们可以使用指数分布(exponential distribution): p(x;λ) λlx≥0exp(-λx)指数分布使用指示函数(indicator function) lx≥…
肖仰华:知识图谱构建的三要素、三原则和九大策略 | AI ProCon 2019
演讲嘉宾 | 肖仰华(复旦大学教授、博士生导师,知识工场实验室负责人) 编辑 | Jane 出品 | AI科技大本营(ID:rgznai100) 近两年,知识图谱技术得到了各行各业的关注,无论是企业公司还…

Docker mongo副本集环境搭建
1、MongoDB Docker 镜像安装 docker pull mongo 2、Docker容器创建 MongoDB Docker 容器创建有以下几个问题: 1- MongoDB 容器基本创建方法和数据目录挂载 2- MongoDB 容器的数据迁移 3- MongoDB 设置登录权限问题docker run -p 27017:27017 -v <LocalDirectoryP…

菜鸟学习HTML5+CSS3(一)
主要内容: 1.新的文档类型声明(DTD) 2.新增的HTML5标签 3.删除的HTML标签 4.重新定义的HTML标签 一、新的文档类型声明(DTD) HTML 5的DTD声明为:<!doctype html>、<!DOCTYPE html>、<!DOCTY…
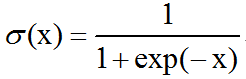
激活函数之logistic sigmoid函数介绍及C++实现
logistic sigmoid函数:logistic sigmoid函数通常用来产生Bernoulli分布中的参数,因为它的范围是(0,1),处在的有效取值范围内。logisitic sigmoid函数在变量取绝对值非常大的正值或负值时会出现饱和(saturate)现象,意味着函数会变得…

NLP重要模型详解,换个方式学(内附资源)
(图片有AI科技大本营付费下载自视觉中国)作者 | Jaime Zornoza,马德里技术大学译者 | 陈之炎校对 | 王威力编辑 | 黄继彦来源 | 数据派THU(ID:DatapiTHU)【导语】本文带你以前所未有的方式了解深度学习神经…
大闸蟹的OO第二单元总结
OO的第二单元是讲多线程的协作与控制,三次作业分别为FAFS电梯,ALS电梯和三部需要协作的电梯。三次作业由浅入深,让我们逐渐理解多线程的工作原理和运行状况。 第一次作业: 第一次作业是傻瓜电梯,也就是完全不需要考虑捎…

构建ASP.NET MVC4+EF5+EasyUI+Unity2.x注入的后台管理系统(31)-MVC使用RDL报表
原文:构建ASP.NET MVC4EF5EasyUIUnity2.x注入的后台管理系统(31)-MVC使用RDL报表这次我们来演示MVC3怎么显示RDL报表,坑爹的微软把MVC升级到5都木有良好的支持报表,让MVC在某些领域趋于短板 我们只能通过一些方式来使用rdl报表。 Razor视图不支持asp.net…

18段代码带你玩转18个机器学习必备交互工具
(图片有AI科技大本营付费下载自视觉中国)作者 | 曼纽尔阿米纳特吉(Manuel Amunategui)、迈赫迪洛佩伊(Mehdi Roopaei)来源 | 大数据(ID:hzdashuju)【导读】本文简要介绍将…
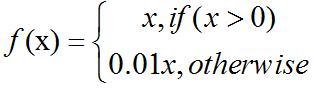
激活函数之ReLU/softplus介绍及C++实现
softplus函数(softplus function):ζ(x)ln(1exp(x)).softplus函数可以用来产生正态分布的β和σ参数,因为它的范围是(0,∞)。当处理包含sigmoid函数的表达式时它也经常出现。softplus函数名字来源于它是另外一个函数的平滑(或”软化”)形式,这…

windows server 2012 用sysdba登录报错 ORA-01031
报错显示:C:\Users\Administrator>sqlplus / as sysdba SQL*Plus: Release 11.2.0.1.0 Production on 星期三 4月 24 09:09:33 2019 Copyright (c) 1982, 2010, Oracle. All rights reserved. ERROR:ORA-01031: 权限不足 请输入用户名: 1、查看本地用户和组确认权…

[SignalR]初步认识以及安装
原文:[SignalR]初步认识以及安装1.什么是ASP.NET SignalR? ASP .NET SignalR是一个 ASP .NET 下的类库,可以在ASP .NET 的Web项目中实现实时通信。什么是实时通信的Web呢?就是让客户端(Web页面)和服务器端可以互相通知…
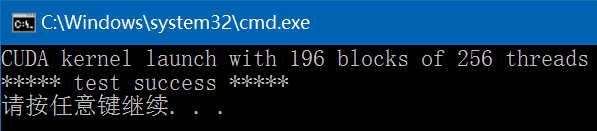
CUDA Samples:Vector Add
以下CUDA sample是分别用C和CUDA实现的两向量相加操作,参考CUDA 8.0中的sample:C:\ProgramData\NVIDIA Corporation\CUDA Samples\v8.0\0_Simple,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:common.hpp:#ifndef FBC_CU…

你和人工智能的对话,正在被人工收听
(图片有AI科技大本营付费下载自视觉中国)作者 | 周晶晶编辑 | 阿伦来源 | 燃财经(ID:rancaijing)如今,智能设备越来越多地出现在每个人的生活中,在享受它们带来的便利时,很多人或许没有意识到&a…

python数据结构与算法总结
python常用的数据结构与算法就分享到此处,本月涉及数据结构与算法的内容有如下文章: 《数据结构和算法对python意味着什么?》 《顺序表数据结构在python中的应用》 《python实现单向链表数据结构及其基本方法》 《python实现单向循环链表数据…

自定义classloader中的接口调用
2019独角兽企业重金招聘Python工程师标准>>> 注意其中转型异常的描述,左边声明和强转括号内都是appclassloader加载的,而让自定义加载类的接口也由appclassloader加载,所以转型成功 转载于:https://my.oschina.net/heatonn1/blog/…

学点基本功:机器学习常用损失函数小结
(图片付费下载自视觉中国)作者 | 王桂波转载自知乎用户王桂波【导读】机器学习中的监督学习本质上是给定一系列训练样本 ,尝试学习 的映射关系,使得给定一个 ,即便这个不在训练样本中,也能够得到尽量接近…

python生成简单的FTP弱口令扫描
2019独角兽企业重金招聘Python工程师标准>>> 前言 Ftp这个类实现了Ftp客户端的大多数功能,比如连接Ftp服务器、查看服务器中的文件、上传、下载文件等功能,Ftp匿名扫描器的实现,需要使用FTP这个类,首先用主机名构造了一个Ftp对象(即ftp),然后用这个ftp调…

C++中const指针用法汇总
这里以int类型为例,进行说明,在C中const是类型修饰符:int a; 定义一个普通的int类型变量a,可对此变量的值进行修改。const int a 3;与 int const a 3; 这两条语句都是有效的code,并且是等价的,说明a是一个…

mongodb基础应用
一些概念 一个mongod服务可以有建立多个数据库,每个数据库可以有多张表,这里的表名叫collection,每个collection可以存放多个文档(document),每个文档都以BSON(binary json)的形式存…

【leetcode】1030. Matrix Cells in Distance Order
题目如下: We are given a matrix with R rows and C columns has cells with integer coordinates (r, c), where 0 < r < R and 0 < c < C. Additionally, we are given a cell in that matrix with coordinates (r0, c0). Return the coordinates of…
深度学习面临天花板,亟需更可信、可靠、安全的第三代AI技术|AI ProCon 2019
整理 | 夕颜 出品 | AI科技大本营(ID:rgznai100) 在人工智能领域中,深度学习掀起了最近一次浪潮,但在实践和应用中也面临着诸多挑战,特别是关系到人的生命,如医疗、自动驾驶等领域场景时,黑盒…

java robot类自动截屏
直接上代码:package robot;import java.awt.Rectangle;import java.awt.Robot;import java.awt.event.InputEvent;import java.awt.p_w_picpath.BufferedImage;import java.io.File;import java.io.IOException;import javax.p_w_picpathio.ImageIO;import com.sun.glass.event…
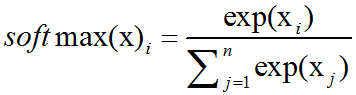
激活函数之softmax介绍及C++实现
下溢(underflow):当接近零的数被四舍五入为零时发生下溢。许多函数在其参数为零而不是一个很小的正数时才会表现出质的不同。例如,我们通常要避免被零除或避免取零的对数。上溢(overflow):当大量级的数被近似为∞或-∞时发生上溢。进一步的运…