学点基本功:机器学习常用损失函数小结

(图片付费下载自视觉中国)
【导读】机器学习中的监督学习本质上是给定一系列训练样本 ,尝试学习
的映射关系,使得给定一个 ,即便这个
不在训练样本中,也能够得到尽量接近真实y的输出
。而损失函数(Loss Function)则是这个过程中关键的一个组成部分,用来衡量模型的输出
与真实y的之间的差距,给模型的优化指明方向。
本文将介绍机器学习、深度学习中分类与回归常用的几种损失函数,包括均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss、Huber Loss、分位数损失 Quantile Loss、交叉熵损失函数 Cross Entropy Loss、Hinge 损失 Hinge Loss。主要介绍各种损失函数的基本形式、原理、特点等方面。
目录
- 前言
- 均方差损失 Mean Squared Error Loss
- 平均绝对误差损失 Mean Absolute Error Loss
- Huber Loss
- 分位数损失 Quantile Loss
- 交叉熵损失 Cross Entropy Loss
- 合页损失 Hinge Loss
- 总结
前言
在正文开始之前,先说下关于 Loss Function、Cost Function 和 Objective Function 的区别和联系。在机器学习的语境下这三个术语经常被交叉使用。
- 损失函数 Loss Function 通常是针对单个训练样本而言,给定一个模型输出
和一个真实
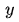 ,损失函数输出一个实值损失
,损失函数输出一个实值损失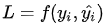
- 代价函数 Cost Function 通常是针对整个训练集(或者在使用 mini-batch gradient descent 时一个 mini-batch)的总损失
- 目标函数 Objective Function 是一个更通用的术语,表示任意希望被优化的函数,用于机器学习领域和非机器学习领域(比如运筹优化)
一句话总结三者的关系就是:A loss function is a part of a cost function which is a type of an objective function(https://stats.stackexchange.com/questions/179026/objective-function-cost-function-loss-function-are-they-the-same-thing).
由于损失函数和代价函数只是在针对样本集上有区别,因此在本文中统一使用了损失函数这个术语,但下文的相关公式实际上采用的是代价函数 Cost Function 的形式,请读者自行留意。
均方差损失 Mean Squared Error Loss
基本形式与原理
均方差 Mean Squared Error (MSE) 损失是机器学习、深度学习回归任务中最常用的一种损失函数,也称为 L2 Loss。其基本形式如下
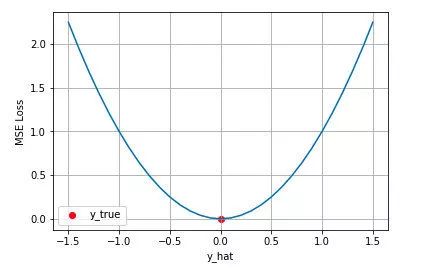
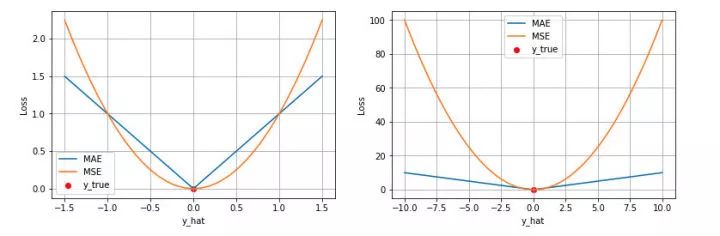
从直觉上理解均方差损失,这个损失函数的最小值为 0(当预测等于真实值时),最大值为无穷大。下图是对于真实值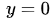 ,不同的预测值
,不同的预测值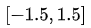 的均方差损失的变化图。横轴是不同的预测值,纵轴是均方差损失,可以看到随着预测与真实值绝对误差
的均方差损失的变化图。横轴是不同的预测值,纵轴是均方差损失,可以看到随着预测与真实值绝对误差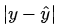 的增加,均方差损失呈二次方地增加。
的增加,均方差损失呈二次方地增加。
背后的假设
实际上在一定的假设下,我们可以使用最大化似然得到均方差损失的形式。假设模型预测与真实值之间的误差服从标准高斯分布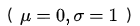 ,则给定一个
,则给定一个 模型输出真实值
的概率为

进一步我们假设数据集中 N 个样本点之间相互独立,则给定所有x输出所有真实值y 的概率,即似然 Likelihood,为所有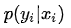 的累乘
的累乘
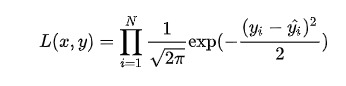
通常为了计算方便,我们通常最大化对数似然 Log-Likelihood
去掉与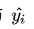 无关的第一项,然后转化为最小化负对数似然 Negative Log-Likelihood
无关的第一项,然后转化为最小化负对数似然 Negative Log-Likelihood
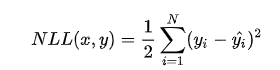
可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下,最小化均方差损失函数与极大似然估计本质上是一致的,因此在这个假设能被满足的场景中(比如回归),均方差损失是一个很好的损失函数选择;当这个假设没能被满足的场景中(比如分类),均方差损失不是一个好的选择。
平均绝对误差损失 Mean Absolute Error Loss
基本形式与原理
平均绝对误差 Mean Absolute Error (MAE) 是另一类常用的损失函数,也称为 L1 Loss。其基本形式如下
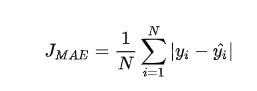
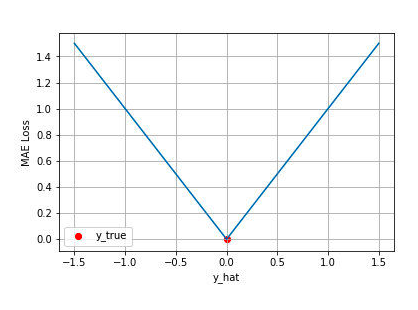
同样的我们可以对这个损失函数进行可视化如下图,MAE 损失的最小值为 0(当预测等于真实值时),最大值为无穷大。可以看到随着预测与真实值绝对误差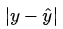 的增加,MAE 损失呈线性增长
的增加,MAE 损失呈线性增长
背后的假设
同样的我们可以在一定的假设下通过最大化似然得到 MAE 损失的形式,假设模型预测与真实值之间的误差服从拉普拉斯分布 Laplace distribution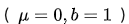 ,则给定一个
,则给定一个 模型输出真实
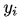 的概率为
的概率为
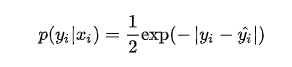
与上面推导 MSE 时类似,我们可以得到的负对数似然实际上就是 MAE 损失的形式
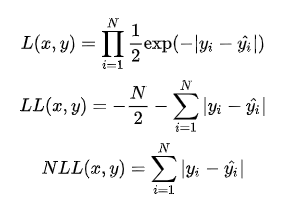
MAE 与 MSE 区别
MAE 和 MSE 作为损失函数的主要区别是:MSE 损失相比 MAE 通常可以更快地收敛,但 MAE 损失对于 outlier 更加健壮,即更加不易受到 outlier 影响。
MSE 通常比 MAE 可以更快地收敛。当使用梯度下降算法时,MSE 损失的梯度为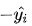 ,而 MAE 损失的梯度为
,而 MAE 损失的梯度为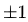 ,即 MSE 的梯度的 scale 会随误差大小变化,而 MAE 的梯度的 scale 则一直保持为 1,即便在绝对误差
,即 MSE 的梯度的 scale 会随误差大小变化,而 MAE 的梯度的 scale 则一直保持为 1,即便在绝对误差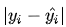 很小的时候 MAE 的梯度 scale 也同样为 1,这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题,但是总的来说,损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。
很小的时候 MAE 的梯度 scale 也同样为 1,这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题,但是总的来说,损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因。
MAE 对于 outlier 更加 robust。我们可以从两个角度来理解这一点:
- 第一个角度是直观地理解,下图是 MAE 和 MSE 损失画到同一张图里面,由于MAE 损失与绝对误差之间是线性关系,MSE 损失与误差是平方关系,当误差非常大的时候,MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时,MSE 会产生一个非常大的损失,对模型的训练会产生较大的影响。
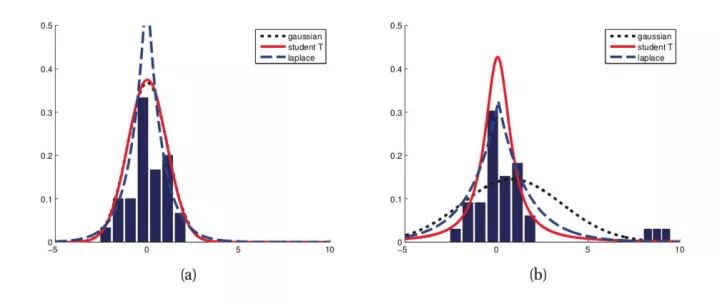
- 第二个角度是从两个损失函数的假设出发,MSE 假设了误差服从高斯分布,MAE 假设了误差服从拉普拉斯分布。拉普拉斯分布本身对于 outlier 更加 robust。参考下图(来源:Machine Learning: A Probabilistic Perspective 2.4.3 The Laplace distribution Figure 2.8),当右图右侧出现了 outliers 时,拉普拉斯分布相比高斯分布受到的影响要小很多。因此以拉普拉斯分布为假设的 MAE 对 outlier 比高斯分布为假设的 MSE 更加 robust。
Huber Loss
上文我们分别介绍了 MSE 和 MAE 损失以及各自的优缺点,MSE 损失收敛快但容易受 outlier 影响,MAE 对 outlier 更加健壮但是收敛慢,Huber Loss 则是一种将 MSE 与 MAE 结合起来,取两者优点的损失函数,也被称作 Smooth Mean Absolute Error Loss 。其原理很简单,就是在误差接近 0 时使用 MSE,误差较大时使用 MAE,公式为
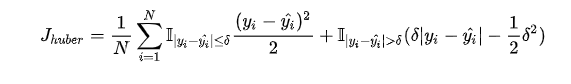
上式中 是 Huber Loss 的一个超参数,
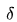 的值是 MSE 和 MAE 两个损失连接的位置。上式等号右边第一项是 MSE 的部分,第二项是 MAE 部分,在 MAE 的部分公式为
的值是 MSE 和 MAE 两个损失连接的位置。上式等号右边第一项是 MSE 的部分,第二项是 MAE 部分,在 MAE 的部分公式为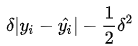 是为了保证误差
是为了保证误差 时 MAE 和 MSE 的取值一致,进而保证 Huber Loss 损失连续可导。
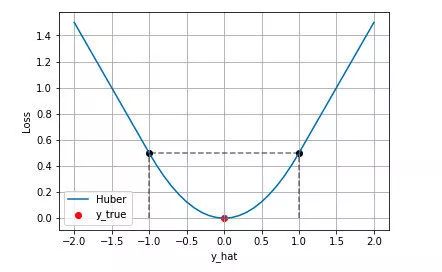
下图是 时的 Huber Loss,可以看到在
的区间内实际上就是 MSE 损失,在
 区间内为 MAE损失。
区间内为 MAE损失。
Huber Loss 的特点
Huber Loss 结合了 MSE 和 MAE 损失,在误差接近 0 时使用 MSE,使损失函数可导并且梯度更加稳定;在误差较大时使用 MAE 可以降低 outlier 的影响,使训练对 outlier 更加健壮。缺点是需要额外地设置一个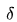 超参数。
超参数。
分位数损失 Quantile Loss
分位数回归 Quantile Regression 是一类在实际应用中非常有用的回归算法,通常的回归算法是拟合目标值的期望或者中位数,而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。例如我们可以分别拟合出多个分位点,得到一个置信区间,如下图所示(图片来自笔者的一个分位数回归代码 demo Quantile Regression Demo)
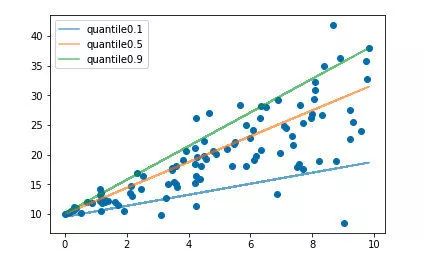
分位数回归是通过使用分位数损失 Quantile Loss 来实现这一点的,分位数损失形式如下,式中的 r 分位数系数。
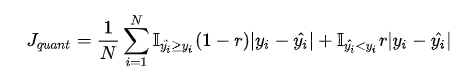
我们如何理解这个损失函数呢?这个损失函数是一个分段的函数 ,将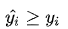 (高估) 和
(高估) 和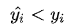 (低估) 两种情况分开来,并分别给予不同的系数。当
(低估) 两种情况分开来,并分别给予不同的系数。当
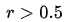 时,低估的损失要比高估的损失更大,反过来当
时,低估的损失要比高估的损失更大,反过来当 时,高估的损失比低估的损失大;分位数损失实现了分别用不同的系数控制高估和低估的损失,进而实现分位数回归。特别地,当
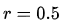 时,分位数损失退化为 MAE 损失,从这里可以看出 MAE 损失实际上是分位数损失的一个特例 — 中位数回归(这也可以解释为什么 MAE 损失对 outlier 更鲁棒:MSE 回归期望值,MAE 回归中位数,通常 outlier 对中位数的影响比对期望值的影响小)。
时,分位数损失退化为 MAE 损失,从这里可以看出 MAE 损失实际上是分位数损失的一个特例 — 中位数回归(这也可以解释为什么 MAE 损失对 outlier 更鲁棒:MSE 回归期望值,MAE 回归中位数,通常 outlier 对中位数的影响比对期望值的影响小)。
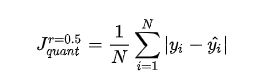
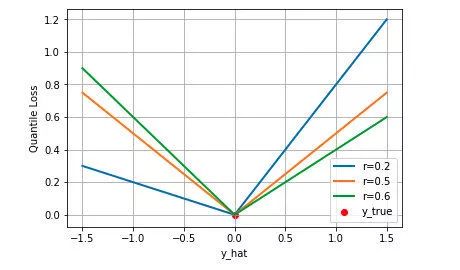
下图是取不同的分位点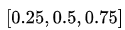 得到的三个不同的分位损失函数的可视化,可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的,而 0.5 实际上就是 MAE。
得到的三个不同的分位损失函数的可视化,可以看到 0.2 和 0.6 在高估和低估两种情况下损失是不同的,而 0.5 实际上就是 MAE。
交叉熵损失 Cross Entropy Loss
上文介绍的几种损失函数都是适用于回归问题损失函数,对于分类问题,最常用的损失函数是交叉熵损失函数 Cross Entropy Loss。
二分类
考虑二分类,在二分类中我们通常使用 Sigmoid 函数将模型的输出压缩到 (0, 1) 区间内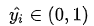 ,用来代表给定输入
,用来代表给定输入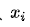 ,模型判断为正类的概率。由于只有正负两类,因此同时也得到了负类的概率。
,模型判断为正类的概率。由于只有正负两类,因此同时也得到了负类的概率。
将两条式子合并成一条
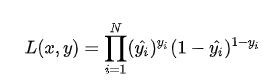
假设数据点之间独立同分布,则似然可以表示为
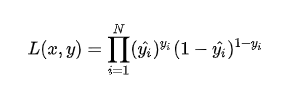
对似然取对数,然后加负号变成最小化负对数似然,即为交叉熵损失函数的形式
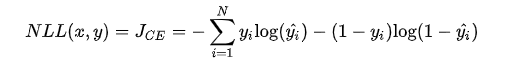
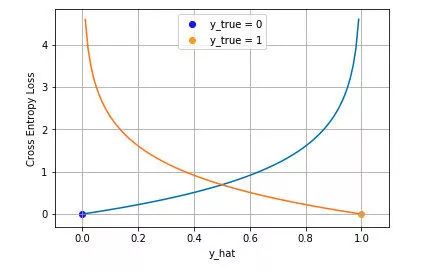
下图是对二分类的交叉熵损失函数的可视化,蓝线是目标值为 0 时输出不同输出的损失,黄线是目标值为 1 时的损失。可以看到约接近目标值损失越小,随着误差变差,损失呈指数增长。
多分类
在多分类的任务中,交叉熵损失函数的推导思路和二分类是一样的,变化的地方是真实值 现在是一个 One-hot 向量,同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在
现在是一个 One-hot 向量,同时模型输出的压缩由原来的 Sigmoid 函数换成 Softmax 函数。Softmax 函数将每个维度的输出范围都限定在 之间,同时所有维度的输出和为 1,用于表示一个概率分布。
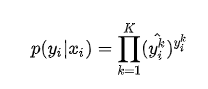
其中 表示 K 个类别中的一类,同样的假设数据点之间独立同分布,可得到负对数似然为
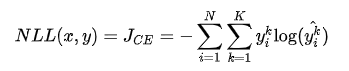
由于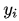 是一个 one-hot 向量,除了目标类为 1 之外其他类别上的输出都为 0,因此上式也可以写为
是一个 one-hot 向量,除了目标类为 1 之外其他类别上的输出都为 0,因此上式也可以写为
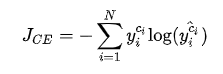
其中 的目标类。通常这个应用于多分类的交叉熵损失函数也被称为 Softmax Loss 或者 Categorical Cross Entropy Loss。
的目标类。通常这个应用于多分类的交叉熵损失函数也被称为 Softmax Loss 或者 Categorical Cross Entropy Loss。
Cross Entropy is good. But WHY?
分类中为什么不用均方差损失?上文在介绍均方差损失的时候讲到实际上均方差损失假设了误差服从高斯分布,在分类任务下这个假设没办法被满足,因此效果会很差。为什么是交叉熵损失呢?有两个角度可以解释这个事情,一个角度从最大似然的角度,也就是我们上面的推导;另一个角度是可以用信息论来解释交叉熵损失:
假设对于样本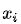 存在一个最优分布
存在一个最优分布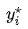 真实地表明了这个样本属于各个类别的概率,那么我们希望模型的输出
真实地表明了这个样本属于各个类别的概率,那么我们希望模型的输出 尽可能地逼近这个最优分布,在信息论中,我们可以使用 KL 散度 Kullback–Leibler Divergence 来衡量两个分布的相似性。给定分布p和和分布q ,两者的 KL 散度公式如下
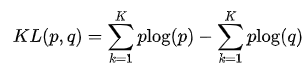
其中第一项为分布p 的信息熵,第二项为分布p 和q 的交叉熵。将最优分布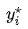 和输出分布
和输出分布 带入p 和
得到
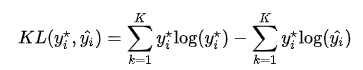
由于我们希望两个分布尽量相近,因此我们最小化 KL 散度。同时由于上式第一项信息熵仅与最优分布本身相关,因此我们在最小化的过程中可以忽略掉,变成最小化
我们并不知道最优分布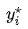 ,但训练数据里面的目标值
,但训练数据里面的目标值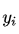 可以看做是
可以看做是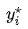 的一个近似分布
的一个近似分布
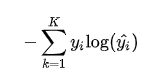
这个是针对单个训练样本的损失函数,如果考虑整个数据集,则
可以看到通过最小化交叉熵的角度推导出来的结果和使用最大 化似然得到的结果是一致的。
合页损失 Hinge Loss
合页损失 Hinge Loss 是另外一种二分类损失函数,适用于 maximum-margin 的分类,支持向量机 Support Vector Machine (SVM) 模型的损失函数本质上就是 Hinge Loss + L2 正则化。合页损失的公式如下
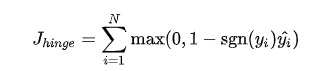
下图是y 为正类, 即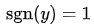 时,不同输出的合页损失示意图
时,不同输出的合页损失示意图
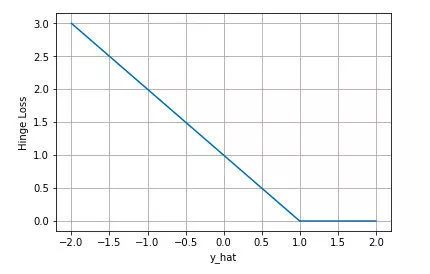
可以看到当y 为正类时,模型输出负值会有较大的惩罚,当模型输出为正值且在(0.1) 区间时还会有一个较小的惩罚。即合页损失不仅惩罚预测错的,并且对于预测对了但是置信度不高的也会给一个惩罚,只有置信度高的才会有零损失。使用合页损失直觉上理解是要找到一个决策边界,使得所有数据点被这个边界正确地、高置信地被分类。
总结
本文针对机器学习中最常用的几种损失函数进行相关介绍,首先是适用于回归的均方差损失 Mean Squared Loss、平均绝对误差损失 Mean Absolute Error Loss,两者的区别以及两者相结合得到的 Huber Loss,接着是应用于分位数回归的分位数损失 Quantile Loss,表明了平均绝对误差损失实际上是分位数损失的一种特例,在分类场景下,本文讨论了最常用的交叉熵损失函数 Cross Entropy Loss,包括二分类和多分类下的形式,并从信息论的角度解释了交叉熵损失函数,最后简单介绍了应用于 SVM 中的 Hinge 损失 Hinge Loss。
本文相关的可视化代码:(https://github.com/borgwang/toys/tree/master/loss_functions)。
受限于时间,本文还有其他许多损失函数没有提及,比如应用于 Adaboost 模型中的指数损失 Exponential Loss,0-1 损失函数等。另外通常在损失函数中还会有正则项(L1/L2 正则),这些正则项作为损失函数的一部分,通过约束参数的绝对值大小以及增加参数稀疏性来降低模型的复杂度,防止模型过拟合,这部分内容在本文中也没有详细展开。读者有兴趣可以查阅相关的资料进一步了解。That’s all. Thanks for reading.?
原文链接:https://zhuanlan.zhihu.com/p/77686118
◆
精彩推荐
◆

推荐阅读
肖仰华:知识图谱构建的三要素、三原则和九大策略 | AI ProCon 2019
微软语音AI技术与微软听听文档小程序实践 | AI ProCon 2019
AI落地遭“卡脖子”困境:为什么说联邦学习是解决良方?
10分钟搭建你的第一个图像识别模型 | 附完整代码
阿里披露AI完整布局,飞天AI平台首次亮相
程序员因接外包坐牢 456 天!两万字揭露心酸经历
限时早鸟票 | 2019 中国大数据技术大会(BDTC)超豪华盛宴抢先看!
Pandas中第二好用的函数 | 优雅的Apply
阿里开源物联网操作系统 AliOS Things 3.0 发布,集成平头哥 AI 芯片架构
雷声大雨点小:Bakkt「见光死」了吗?

你点的每个“在看”,我都认真当成了喜欢
相关文章:

python生成简单的FTP弱口令扫描
2019独角兽企业重金招聘Python工程师标准>>> 前言 Ftp这个类实现了Ftp客户端的大多数功能,比如连接Ftp服务器、查看服务器中的文件、上传、下载文件等功能,Ftp匿名扫描器的实现,需要使用FTP这个类,首先用主机名构造了一个Ftp对象(即ftp),然后用这个ftp调…

C++中const指针用法汇总
这里以int类型为例,进行说明,在C中const是类型修饰符:int a; 定义一个普通的int类型变量a,可对此变量的值进行修改。const int a 3;与 int const a 3; 这两条语句都是有效的code,并且是等价的,说明a是一个…

mongodb基础应用
一些概念 一个mongod服务可以有建立多个数据库,每个数据库可以有多张表,这里的表名叫collection,每个collection可以存放多个文档(document),每个文档都以BSON(binary json)的形式存…

【leetcode】1030. Matrix Cells in Distance Order
题目如下: We are given a matrix with R rows and C columns has cells with integer coordinates (r, c), where 0 < r < R and 0 < c < C. Additionally, we are given a cell in that matrix with coordinates (r0, c0). Return the coordinates of…
深度学习面临天花板,亟需更可信、可靠、安全的第三代AI技术|AI ProCon 2019
整理 | 夕颜 出品 | AI科技大本营(ID:rgznai100) 在人工智能领域中,深度学习掀起了最近一次浪潮,但在实践和应用中也面临着诸多挑战,特别是关系到人的生命,如医疗、自动驾驶等领域场景时,黑盒…

java robot类自动截屏
直接上代码:package robot;import java.awt.Rectangle;import java.awt.Robot;import java.awt.event.InputEvent;import java.awt.p_w_picpath.BufferedImage;import java.io.File;import java.io.IOException;import javax.p_w_picpathio.ImageIO;import com.sun.glass.event…
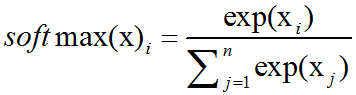
激活函数之softmax介绍及C++实现
下溢(underflow):当接近零的数被四舍五入为零时发生下溢。许多函数在其参数为零而不是一个很小的正数时才会表现出质的不同。例如,我们通常要避免被零除或避免取零的对数。上溢(overflow):当大量级的数被近似为∞或-∞时发生上溢。进一步的运…
parsing:NLP之chart parser句法分析器
已迁移到我新博客,阅读体验更佳parsing:NLP之chart parser句法分析器 完整代码实现放在我的github上:click me 一、任务要求 实现一个基于简单英语语法的chart句法分析器。二、技术路线 采用自底向上的句法分析方法,简单的自底向上句法分析效率不高,常常…

图解Python算法
普通程序员,不学算法,也可以成为大神吗?对不起,这个,绝对不可以。可是算法好难啊~~看两页书就想睡觉……所以就不学了吗?就一直当普通程序员吗?如果有一本算法书,看着很轻松……又有…

详解SSH框架的原理和优点
Struts的原理和优点. Struts工作原理 MVC即Model-View-Controller的缩写,是一种常用的设计模式。MVC 减弱了业务逻辑接口和数据接口之间的耦合,以及让视图层更富于变化。MVC的工作原理,如下图1所示:Struts 是MVC的一种实现࿰…

Numpy and Matplotlib
Numpy介绍 编辑 一个用python实现的科学计算,包括:1、一个强大的N维数组对象Array;2、比较成熟的(广播)函数库;3、用于整合C/C和Fortran代码的工具包;4、实用的线性代数、傅里叶变换和随机数生成…
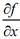
梯度下降法简介
条件数表征函数相对于输入的微小变化而变化的快慢程度。输入被轻微扰动而迅速改变的函数对于科学计算来说可能是有问题的,因为输入中的舍入误差可能导致输出的巨大变化。大多数深度学习算法都涉及某种形式的优化。优化指的是改变x以最小化或最大化某个函数f(x)的任务…

微软亚研院CV大佬代季峰跳槽商汤为哪般?
整理 | 夕颜出品 | AI科技大本营(ID:rgznai100)近日,知乎上一篇离开关于MSRA(微软亚洲研究院)和MSRA CV未来发展的帖子讨论热度颇高,这个帖子以MSRA CV执行研究主任代季峰离职加入商汤为引子,引…

iOS Block实现探究
2019独角兽企业重金招聘Python工程师标准>>> 使用clang的rewrite-objc filename 可以将有block的c代码转换成cpp代码。从中可以看到block的实现。 #include <stdio.h> int main() {void (^blk)(void) ^{printf("Block\n");};blk();return 0; } 使…

CUDA Samples: Long Vector Add
以下CUDA sample是分别用C和CUDA实现的两个非常大的向量相加操作,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:common.hpp:#ifndef FBC_CUDA_TEST_COMMON_HPP_ #define FBC_CUDA_TEST_COMMON_HPP_#include<random>template&l…

TensorFlow2.0正式版发布,极简安装TF2.0(CPUGPU)教程
作者 | 小宋是呢转载自CSDN博客【导读】TensorFlow 2.0,昨天凌晨,正式放出了2.0版本。不少网友表示,TensorFlow 2.0比PyTorch更好用,已经准备全面转向这个新升级的深度学习框架了。本篇文章就带领大家用最简单地方式安装TF2.0正式…

javascript全栈开发实践-准备
目标: 我们将会通过一些列教程,在只使用JavaScript开发的情况下,实现一个手写笔记应用。该应用具有以下特点: 全平台,有手机客户端(Android/iOS),Windows,macOSÿ…

POJ 1017 Packets 贪心 模拟
一步一步模拟,做这种题好累 先放大的的,然后记录剩下的空位有多少,塞1*1和2*2的进去 //#pragma comment(linker, "/STACK:1024000000,1024000000") #include<cstdio> #include<cstring> #include<cstdlib> #incl…

NLP被英语统治?打破成见,英语不应是「自然语言」同义词
(图片付费下载自视觉中国)作者 | Emily M. Bender译者 | 陆离责编 | 夕颜出品 | AI科技大本营(ID: rgznai100) 【导读】在NLP领域,多资源语言以英语、汉语(普通话)、阿拉伯语和法语为代表&#…

CUDA Samples: Dot Product
以下CUDA sample是分别用C和CUDA实现的两个非常大的向量实现点积操作,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:common.hpp:#ifndef FBC_CUDA_TEST_COMMON_HPP_ #define FBC_CUDA_TEST_COMMON_HPP_#include<random>templa…

element ui只输入数字校验
注意:圈起来的两个地方,刚开始忘记写typenumber了,导致可以输入‘123abc’这样的,之后加上了就OK了 转载于:https://www.cnblogs.com/samsara-yx/p/10774270.html

对DeDecms之index.php页面的补充
2019独角兽企业重金招聘Python工程师标准>>> 1、301是什么? 其实就是HTTP状态表。就是当用户输入url请求时,服务器的一个反馈状态。 详细链接http://www.cnblogs.com/kunhony/archive/2006/06/16/427305.html 2、common.inc.php和arc.partvi…
OpenCV-Python:K值聚类
关于K聚类,我曾经在一篇博客中提到过,这里简单的做个回顾。 KMeans的步骤以及其他的聚类算法 K-均值是因为它可以发现k个不同的簇,且每个簇的中心采用簇中所含值的均值计算 其他聚类算法:二分K-均值 讲解一下步骤,其实…

CUDA Samples: Julia
以下CUDA sample是分别用C和CUDA实现的绘制Julia集曲线,并对其中使用到的CUDA函数进行了解说,code参考了《GPU高性能编程CUDA实战》一书的第四章,各个文件内容如下:funset.cpp:#include "funset.hpp" #include <rand…

给初学者的深度学习入门指南
从无人驾驶汽车到AlphaGo战胜人类,机器学习成为了当下最热门的技术。而机器学习中一种重要的方法就是深度学习。作为一个有理想的程序员,若是不懂人工智能(AI)领域中深度学习(DL)这个超热的技术,…

epoll/select
为什么80%的码农都做不了架构师?>>> epoll相对select优点主要有三: 1. select的句柄数目受限,在linux/posix_types.h头文件有这样的声明:#define __FD_SETSIZE 1024 表示select最多同时监听1024个fd。而epoll没…

CUDA Samples: ripple
以下CUDA sample是分别用C和CUDA实现的生成的波纹图像,并对其中使用到的CUDA函数进行了解说,code参考了《GPU高性能编程CUDA实战》一书的第五章,各个文件内容如下:funset.cpp:#include "funset.hpp" #includ…

Python告诉你这些旅游景点好玩、便宜、人又少!
(图片由CSDN付费下载自东方IC)作者 | 猪哥来源 | 裸睡的猪(ID:IT--Pig) 2019年国庆马上就要到来,今年来点新花样吧,玩肯定是要去玩的,不然怎么给祖国庆生?那去哪里玩&…
手机APP自动化之uiautomator2 +python3 UI自动化
题记: 之前一直用APPium直到用安卓9.0 发现uiautomatorviewer不支持安卓 9.0,点击截屏按钮 一直报错,百度很久解决方法都不可以,偶然间看见有人推荐:uiautomator2 就尝试使用 发现比appium要简单一些; 下面…

爱上MVC3系列~开发一个站点地图(俗称面包屑)
回到目录 原来早在webform控件时代就有了SiteMap这个东西,而进行MVC时代后,我们也希望有这样一个东西,它为我们提供了不少方便,如很方便的实现页面导航的内容修改,页面导航的样式换肤等. 我的MvcSiteMap主要由实体文件,XML配置文件,C#调用文件组成,当然为了前台使用方便,可以为…
