【Leetcode】 刷题之路1(python)
leetcode 刷题之路1(python)
看到有大佬总结了一些相关题目,想着先刷一类。
- 1.两数之和
- 15.三数之和
- 16.最接近的三数之和
- 11.盛最多的水
- 18.四数之和
- 454.四数相加II
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
-2 <= nums.length <= 10^4
-10^9<= nums[i] <= 10^9
-10^9 <= target <= 10^9
只会存在一个有效答案
题解
看了大神的一些解体参考,暴力破解法双层for循环查找的话,时间复杂度是O(n^2),会出现RuntimeOver。
方法一:用python的list相关函数求解
该题的解决方案是找到 num2 = target - num1是否在该list中,如果num2在list中查找出其下标,并返回。
- num2 in nums,返回 True
- nums.index(num2),查找 num2 的索引
这样需要对于每一个num1,对整个nums列表做一次啊查询,为了提高时间复杂度,num2 的查找并不需要每次从 nums 查找一遍,只需要从 num1 位置之前或之后查找即可。这里选择从num1位置之前的元素中找。
def twoSum(nums, target):lens = len(nums)j=-1for i in range(1,lens):temp = nums[:i]if (target - nums[i]) in temp:j = temp.index(target - nums[i])breakif j>=0:return [j,i]
方法二:直接使用字典求解
用字典的方法进行求解,使用enumerate枚举所有元素,省去了查找索引,效率很快
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:records = dict() #创建空字典# 用枚举更方便,就不需要通过索引再去取当前位置的值for idx, val in enumerate(nums):if target - val not in records:records[val] = idxelse:return [records[target - val], idx] # 如果存在就返回字典记录索引和当前索引
方法三:用字典模拟哈希求解
参考了大神们的解法,通过哈希来求解,这里通过字典来模拟哈希查询的过程。其实就是字典记录了 num1 和 num2 的值和位置,不需要再去查询一遍索引的步骤。
def twoSum(nums, target):hashmap={}for ind,num in enumerate(nums):hashmap[num] = indfor i,num in enumerate(nums):j = hashmap.get(target - num)if j is not None and i!=j:return [i,j]
小话痨:开始使用python刷题啦(最近在学机器学习),用leetcode边刷题,边练python,顺便写点小总结。
这题,让我记住了python中list(列表)类型、dictonary(字典)类型、内置函数enumerate。
enumerate(sequence, [start=0])
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
题解
虽然题目意思和两数之和类似,但看了官方题解和做法后,发现用的方法不尽相同。
任意一个三元组的和都为 0。如果直接使用三重循环枚举三元组,会得到 O(N3)个满足题目要求的三元组(其中 NN 是数组的长度)时间复杂度至少为 O(N^3)。在这之后,我们还需要使用哈希表进行去重操作,得到不包含重复三元组的最终答案,又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高,因此我们要换一种思路来考虑这个问题。
排序+双指针
该提要求不重复的三元组,不重复,也就是说,我们枚举的三元组 (a, b, c)需要满足a ≤ b ≤ c,保证了只有 (a, b, c) 这个顺序会被枚举到。要实现这一点,我们可以将数组中的元素从小到大进行排序,随后使用普通的三重循环就可以满足上面的要求。
同时,对于每一重循环而言,相邻两次枚举的元素不能相同,否则也会造成重复。举个例子,如果排完序的数组为 [0, 1, 2, 2, 2, 3] ,我们使用三重循环枚举到的第一个三元组为 (0, 1, 2),如果第三重循环继续枚举下一个元素,那么仍然是三元组 (0, 1, 2),产生了重复。因此我们需要将第三重循环跳到下一个不相同的元素,即数组中的最后一个元素 3,枚举三元组 (0, 1, 3)。
这种方法的时间复杂度仍然为 O(N^3),毕竟我们还是没有跳出三重循环的大框架。然而它是很容易继续优化的,可以发现,如果我们固定了前两重循环枚举到的元素 a 和 b,那么只有唯一的 c 满足 a+b+c=0。当第二重循环往后枚举一个元素 b’ 时,由于 b’ > b,那么满足 a+b’+c’=0 的 c’ 一定有 c’ < c,即 c’ 在数组中一定出现在 c 的左侧。也就是说,我们可以从小到大枚举 b,同时从大到小枚举 c,即第二重循环和第三重循环实际上是并列的关系。
有了这样的发现,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针。并且,保持左指针一直在右指针的左侧(即满足 b≤c)。
这个方法就是我们常说的双指针,当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法。
(看了官方题解和大佬的题解,我认为同一种方法大佬的代码更加简单易理解)
class Solution:def threeSum(self, nums: List[int]) -> List[List[int]]:n=len(nums)if(not nums or n<3):return []nums.sort()res=[]for i in range(n):if(nums[i]>0): # 如果第一个数就大于0,排序后的两个数不可能使得三个数=0return resif(i>0 and nums[i]==nums[i-1]):continueL=i+1R=n-1while(L<R):if(nums[i]+nums[L]+nums[R]==0):res.append([nums[i],nums[L],nums[R]])while(L<R and nums[L]==nums[L+1]):L=L+1 # b的指针右移动while(L<R and nums[R]==nums[R-1]):R=R-1 # c的指针左移# 找下一个符合条件的L=L+1R=R-1elif(nums[i]+nums[L]+nums[R]>0):R=R-1else:L=L+1return res复杂度分析
- 时间复杂度:O(N^2),其中 N 是数组 nums 的长度。数组排序O(NlogN)
- 空间复杂度:O(logN)。我们忽略存储答案的空间,额外的排序的空间复杂度为 O(logN)。然而我们修改了输入的数组 nums,在实际情况下不一定允许,因此也可以看成使用了一个额外的数组存储了nums 的副本并进行排序,空间复杂度为 O(N)。
16. 最接机的三数之和
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
题解
这道题虽与上一道相似,但实际上因为a+b+c=0有不少特殊性质,并不能完全借鉴思路。
这道题的题目比较短,获取最接近target目标值的三数之和。
首先拿到这种题,我们要先看下提示中的取值范围,3 <= nums.length <= 103条件标志着。不会出现不足三个数字的异常场景,但103 如果三层for循环109必然会超时,暴力解法不通。
那么,下来就需要考虑优化方案:
- 二分查找 or hash表?
二分查找和hash表只针对单个数字,那势必我们需要先双层循环再二分,10^6一样会超时。 - 缩减条件
既然三个数字我们有些无从下手,那么先使用一层for循环,减少一个数字的筛选再来考虑是否就简单了一些。
减少一个数字后,我们的题目变成了查找数组中某两个最接近target - num1,就变成了一道两数之和的基础题。 - 实现方案
我们先将nums排序;
设置返回值res,初始为无穷大;
循环开始:从第一个数nums[i]后的数开始,设置left = i + 1, right = length - 1;tmp = nums[left] + nums[rigth]
比较 res和tmp+nums[i],哪个更接近target,并赋值给res
如果tmp = target - nums[i],表示找到了三个数等于target直接返回target
如果tmp > target - nums[i],我们将right向左移一个
如果tmp < target - nums[i],我们将left向右移一个
最终,即可获取结果。
排序+双指针
同时,借鉴上一道题,可以直接将其移动到下一个与这次枚举到的不相同的元素,减少枚举的次数,缩短时间。(但这样会消耗内存)
class Solution:def threeSumClosest(self, nums: List[int], target: int) -> int:ret = float('inf')nums.sort()length = len(nums)for i in range(length - 2):left = i + 1right = length - 1while left < right:tmp = nums[i] + nums[left] + nums[right]ret = tmp if abs(tmp - target) < abs(ret - target) else ret #取更近的if tmp == target:return targetif tmp > target:r = right - 1# 移动到下一个不相等的元素while left < r and nums[r] == nums[right]:r -= 1right = r# right- =1else:# 如果和小于 target,移动 left 对应的指针l = left + 1# 移动到下一个不相等的元素while l < right and nums[l] == nums[left]:l += 1left = l#left- =1return ret
11. 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
题解
这一题使用:双指针。
容纳的水量=两个指针指向的数字中较小值*指针之间的距离
至于怎么移动前后两个指针?
如果我们移动数字较大的那个指针,那么前者「两个指针指向的数字中较小值」不会增加,后者「指针之间的距离」会减小,那么这个乘积会减小。因此,我们移动数字较大的那个指针是不合理的。因此,我们移动数字较小的那个指针。
以示例为例:在初始时[1, 8, 6, 2, 5, 4, 8, 3, 7],左右指针分别指向数组的左右两端,它们可以容纳的水量为 min(1, 7) * 8 =8。我们将左指针向右移动,此时可以容纳的水量为 min(8, 7) * 7 =49。
class Solution:def maxArea(self, height: List[int]) -> int:l, r = 0, len(height) - 1ans = 0while l < r:area = min(height[l], height[r]) * (r - l)ans = max(ans, area)if height[l] <= height[r]:l += 1else:r -= 1return ans
18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
- 0 <= a, b, c, d < n
- a、b、c 和 d 互不相同
- nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
题解
方法一
本题与「15. 三数之和」相似,解法也相似。排序+双指针
为了避免枚举到重复四元组,则需要保证每一重循环枚举到的元素不小于其上一重循环枚举到的元素,且在同一重循环中不能多次枚举到相同的元素。
为了实现上述要求,可以对数组进行排序,并且在循环过程中遵循以下两点:
- 每一种循环枚举到的下标必须大于上一重循环枚举到的下标;
- 同一重循环中,如果当前元素与上一个元素相同,则跳过当前元素。
使用上述方法,可以避免枚举到重复四元组,但是由于仍使用四重循环,时间复杂度仍是 O(n^4)。注意到数组已经被排序,因此可以使用双指针的方法去掉一重循环。
使用两重循环分别枚举前两个数,然后在两重循环枚举到的数之后使用双指针枚举剩下的两个数。假设两重循环枚举到的前两个数分别位于下标 i 和 j,其中 i<j。初始时,左右指针分别指向下标 j+1 和下标 n-1。每次计算四个数的和,并进行如下操作:
- 如果和等于 target,则将枚举到的四个数加到答案中,然后将左指针右移直到遇到不同的数,将右指针左移直到遇到不同的数;
- 如果和小于 target,则将左指针右移一位;
- 如果和大于 target,则将右指针左移一位。
具体实现时,还可以进行一些剪枝操作:
- 在确定第一个数之后,如果nums[i]+nums[i+1]+nums[i+2]+nums[i+3]>target,说明此时剩下的三个数无论取什么值,四数之和一定大于target,因此退出第一重循环;
- 在确定第一个数之后,如果nums[i]+nums[n−3]+nums[n−2]+nums[n−1]<target,说明此时剩下的三个数无论取什么值,四数之和一定小于 target,因此第一重循环直接进入下一轮,枚举nums[i+1];
- 在确定前两个数之后,如果nums[i]+nums[j]+nums[j+1]+nums[j+2]>target,说明此时剩下的两个数无论取什么值,四数之和一定大于target,因此退出第二重循环;
- 在确定前两个数之后,如果 nums[i]+nums[j]+nums[n−2]+nums[n−1]<target,说明此时剩下的两个数无论取什么值,四数之和一定小于 target,因此第二重循环直接进入下一轮,枚举 nums[j+1]。
class Solution:def fourSum(self, nums: List[int], target: int) -> List[List[int]]:quadruplets = list()if not nums or len(nums) < 4:return quadrupletsnums.sort()length = len(nums)for i in range(length - 3):if i > 0 and nums[i] == nums[i - 1]:continueif nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target:breakif nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target:continuefor j in range(i + 1, length - 2):if j > i + 1 and nums[j] == nums[j - 1]:continueif nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target:breakif nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target:continueleft, right = j + 1, length - 1while left < right:total = nums[i] + nums[j] + nums[left] + nums[right]if total == target:quadruplets.append([nums[i], nums[j], nums[left], nums[right]])while left < right and nums[left] == nums[left + 1]:left += 1left += 1while left < right and nums[right] == nums[right - 1]:right -= 1right -= 1elif total < target:left += 1else:right -= 1return quadruplets
复杂度分析
- 时间复杂度:O(n^3),其中 n 是数组的长度。
排序的时间复杂度是O(nlogn),枚举四元组的时间复杂度是 O(n^3) - 空间复杂度:O(logn),其中 n 是数组的长度。
空间复杂度主要取决于排序额外使用的空间。此外排序修改了输入数组 nums,实际情况中不一定允许,因此也可以看成使用了一个额外的数组存储了数组 nums 的副本并排序,空间复杂度为O(n)。
方法二
看了大佬的解法,不用指针不用指针!!回溯解法
思路:
1.对所有数字来说,都有选择,和不选择两种情况。
2. 选择一个数,target就减去这个数,最后target == 0,并且只选择了4个数就结束。
3. 不选择这个数,就去检查下一个数
剪枝很重要!!!
如果排序了数组nums之后。
- 当我们选了这个数,但是选了它之后,即时后面连选全数组最大的数,也不能达到target。就是说,我们当前这个数太小了。这时候,可以肯定这个数是一定不用选择的。
target - nums[i] - (3 - len(oneSolution)) * nums[-1] > 0 - 我们当前的数组的基础上,连续选择当前这个数的话,整体的解的和会比target大,由于我们提前排序了nums,往后去寻找其他的数,只会比当前的数更大,所以这种情况下,我们就不需要往后再去找了。
target - (4 - len(oneSolution)) * nums[i] < 0
但该方法时间复杂度比方法一高高
class Solution:def fourSum(self, nums: List[int], target: int) -> List[List[int]]:nums.sort()output = []def Search(i, target, oneSolution, notSelected):if target == 0 and len(oneSolution) == 4:output.append(oneSolution)returnelif len(oneSolution) > 4 or i >= len(nums):returnif target - nums[i] - (3 - len(oneSolution)) * nums[-1] > 0 or nums[i] in notSelected:Search(i + 1, target, oneSolution, notSelected)elif target - (4 - len(oneSolution)) * nums[i] < 0:returnelse:Search(i + 1, target, oneSolution, notSelected + [nums[i]])Search(i + 1, target - nums[i], oneSolution + [nums[i]], notSelected)Search(0, target, [], [])return output
454.四数相加II
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
- 0 <= i, j, k, l < n
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
(0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
(1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
题解
和18.四数之和不同的是,这题题是从四个数组中各取一个数。
且要求的输出是一共有多少个元组
方法一
我们可以将四个数组分成两部分,A 和 B 为一组,C 和 D 为一组。
对于 A 和 B,我们使用二重循环对它们进行遍历,得到所有 A[i]+B[j] 的值并存入哈希映射中。对于哈希映射中的每个键值对,每个键表示一种 A[i]+B[j],对应的值为 A[i]+B[j] 出现的次数。
对于 C 和 D,我们同样使用二重循环对它们进行遍历。当遍历到 C[k]+D[l] 时,如果 −(C[k]+D[l]) 出现在哈希映射中,那么将 −(C[k]+D[l]) 对应的值累加进答案中。
最终即可得到满足 A[i]+B[j]+C[k]+D[l]=0 的四元组数目。
class Solution:def fourSumCount(self, A: List[int], B: List[int], C: List[int], D: List[int]) -> int:dic = collections.Counter(u + v for u in A for v in B)return sum(dic.get(- c - d, 0) for c in C for d in D)
复杂度分析
时间复杂度:O(n^2)。
我们使用了两次二重循环,时间复杂度均为 O(n^2)。在循环中对哈希映射进行的修改以及查询操作的期望时间复杂度均为 O(1)。空间复杂度:O(n^2),即为哈希映射需要使用的空间。
在最坏的情况下,A[i]+B[j] 的值均不相同,因此值的个数为 n^2,也就需要 O(n^2)的空间
关于Python中collections模块
这个模块实现了特定目标的容器,以提供Python标准内建容器 dict、list、set、tuple 的替代选择。
- Counter:字典的子类,提供了哈希对象的计数功能
- defaultdict:字典的子类,提供了一个工厂函数,为字典查询提供了默认值
- OrderedDict:字典的子类,保留了他们被添加的顺序
- namedtuple:创建命名元组子类的工厂函数
- deque:类似列表容器,实现了在两端快速添加(append)和弹出(pop)
- ChainMap:类似字典的容器类,将多个映射集合到一个视图里面
相关文章:
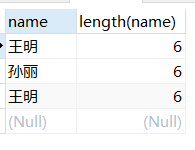
MySQL数据库中的内置函数
SQL函数分为单行函数和多行函数: 单行函数: 红色标注的为重点。 … … … …字符串函数: … … … … … … … … … … 1.length() 存储长度 … … … … … … … … … … 2.char_length() 字符个数 … … … … … … … … … … 3.concat()首尾相连 … ……

elasticsearch从入门到出门-01windows上安装使用
elasticsearch 1、安装JDK,至少1.8.0_73以上版本,java -version2、下载和解压缩Elasticsearch安装包,目录结构3、启动Elasticsearch:bin\elasticsearch.bat,es本身特点之一就是开箱即用,如果是中小型应…

读django文档——Managing static files (e.g. images, JavaScript, CSS)
在上一篇读django文档——nginx uwsgi 部署django项目_苦行僧的妖孽日常-CSDN博客 部署django项目后,发现在runserver时都能正常部署的 static 文件都没有生效。查看文档解决该问题,记录这一过程。 If you use django.contrib.staticfiles as explaine…

pytorch中tensor.mul()和mm()和matmul()
tensor.mul tensor.mul和tensor * tensor 都是将矩阵的对应位置的元素相乘,因此要求维度相同,点乘torch.mul(input, other, *, outNone) → Tensor 参数: input (Tensor) – the input tensor. other (Tensor or Number) torch.mul(input, …
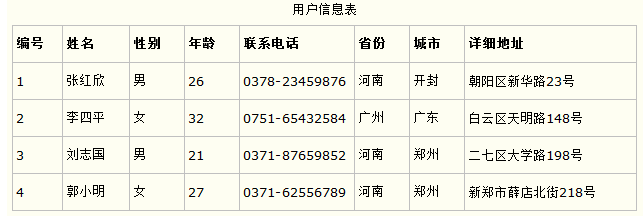
python学习笔记 day44 数据库三范式
参考自 https://www.cnblogs.com/wangfengming/articles/7929118.html 1. 数据库三范式概念: 为了建立减少冗余,结构合理的数据库,涉及数据库时必须要遵守一定的规则,在关系数据库中,这种规则就成为范式,范…

行内标签(最常用的:a标签、img标签、span标签)
a 标签: 功能: 从一个页面跳转到其他页面,或者是当前页面的其他位置。 属性: href :指定跳转的目标路径。 值可以是一个外部网站的地址;也可以是一个内部网页的地址 target: _self 默认值,在当…

SAP HR模块配置假期日历和缺勤类型
目录 一、配置假期日历 二、配置缺勤信息类型 2.1、定义缺勤类型 2.2、定义缺勤的计算规则 2.3、分配缺勤计算规则到缺勤类型 一、配置假期日历 SAP的HR模块中,业务顾问在实施的时候一般会配置未来10年的假期日历,到期后再进行配置。 延长假期日…
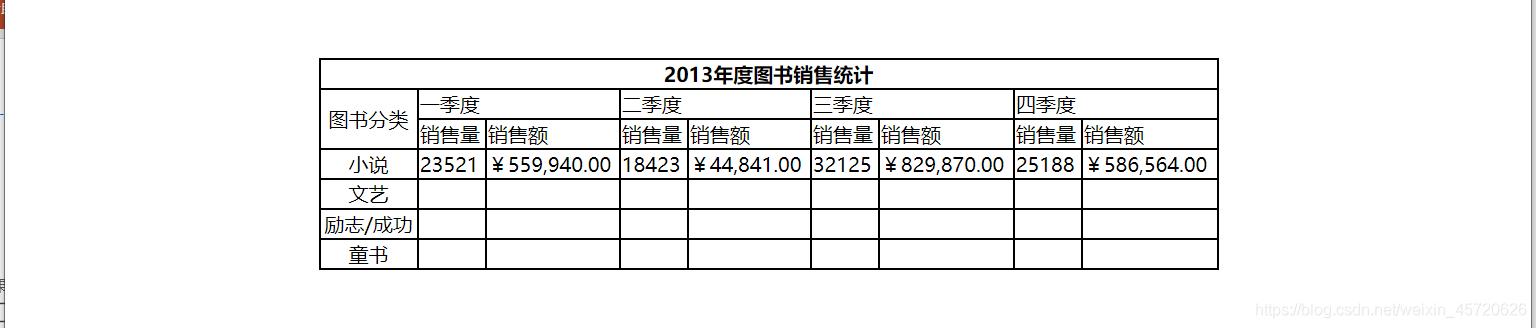
表格(table、tr、th、td、colspan、rowspan)
表格一: <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title></title><style>table{width: 720px;/*设置表格水平宽度为720px*/margin: 0 auto;/*使表格水平居中*/border: 1px solid black;/*设置边框…

Java基础概念性的知识总结
属于个人的所学的知识总结,不是全面的 1.JDK、JRE和JVM三者的区别 01.JDK:(Java Development ToolKit)Java开发工具包,是整个Java的核心。包括了Java的运行环境、JRE、一堆Java工具和Java基础的类库。 02.JRE:(Java Runtime Envir…

vue里的数据
背景: 一个项目完工在即,鉴于此,前端使用了vue,写下此栏,以供日后翻阅, 会涉及到我所运用到的vue相关知识,需要一定的js基础。 默认vue的single-file-components(单文件组件开发&…

【Leetcode】刷题之路2(python)
哈希映射类题目(简单题小试牛刀啦bhn) 242.有效的字母异位词349.两个数组的交集1002.查找常用字符202.快乐数383.赎金信 242. 有效的字母异位词 用python的Counter类太绝了!!! 一行代码解决问题,这道题实…

ORA-01113 file 1 needs media recovery
启动数据库时报错。ORA-01113 datafile1需要恢复。 rman执行恢复。恢复后尝试打开数据库,看结果 rman target / recover datafile 1; alter database open; 反复上述过程,直到所有数据文件恢复。 recover datafile 1; …… recover datafile 13; 如果…

大数据批量导入,解决办法,实践从定时从 sqlserver 批量同步数据到 mySql
c#代码,批量导入数据代码 public class MySql_Target : ZFCommon.DataAccesser.Base.DABase{public MySql_Target(){this.InitDataAccesser(ZFCommon.DataAccesser.DatabaseType.MySql, ReadConfig.TargetConnection);}///大批量数据插入,返回成功插入行数 /// <…

【目标检测】yolo系列:从yolov1到yolov5之YOLOv5训练自己数据集(v6.0)
一、源码下载及requirments 源码下载地址:https://github.com/ultralytics/yolov5 (持续更新中) 本人所用环境如下: pytorch:1.8(因为cuda版本用了pytorch1.8) cuda:10.1 Python&am…

CSS之常用选择器(元素、id、类、通配选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*1、元素选择器作用:根据标签名来选中指定的元素语法:标签名{}例子:p{} h1{} div{}*//*p{color: red;}*/…

Java中 实体类 VO、 PO、DO、DTO、 BO、 QO、DAO、POJO的概念
PO(persistant object) 持久对象 在 o/r 映射的时候出现的概念,如果没有 o/r 映射,没有这个概念存在了。通常对应数据模型 ( 数据库 ), 本身还有部分业务逻辑的处理。可以看成是与数据库中的表相映射的 java 对象。最简单的 PO 就是对应数据库中某个表中…
SAP有用的NOTE(持续更新)
目录 2421240 - Portal is not loaded on Chrome 56 or higher. 66971 - Supported SAP GUI platforms 66971 - Supported SAP GUI platforms 1999880 - FAQ: SAP HANA System Replication 2250144 - FAQ: SAP HANA Secure User Store 2222200 - FAQ: SAP HANA Network …
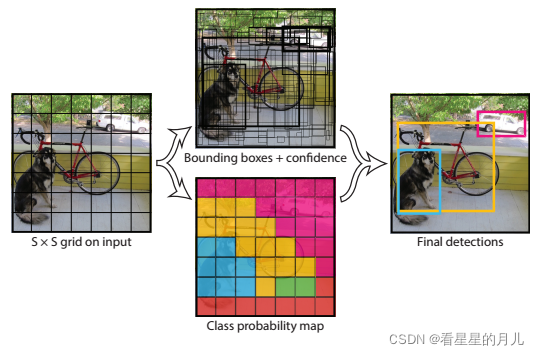
【目标检测】yolo系列:从yolov1到yolov5之YOLOv1详解及复现
检测器通常能够被分为两类,一类是two-stage检测器,最具代表的为faster R-CNN;另一类是one-stage检测器,包括YOLO,SSD等。一般来说,two-stage检测器具有高定位和识别准确性,而one-stage则有速度上…

Ubuntu终端命令行缩短显示路径
平时我们使用linux终端命令行的时候,常常会被一个问题困扰,那就是文件路径过长, 有时候甚至超过了一行,这样看起来非常别扭,其实只要两步就可以解决这个问题: 1,修改.bashrc文件(用户…

主要的约瑟夫环问题
解说 http://poj.org/problem?id3517 n个人,编号为1~n。每次从1開始数,数到m的人出圈。最后一个出圈的人的编号。f[1] 0; for(int i 2; i < n; i) {f[i] ( f[i-1] m)%i; } printf("%d\n",f[n]1);这里第一次出圈的人的编号是mÿ…

CSS之复合选择器(交集、并集选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*将class为red的元素设置为红色*/.red{color: red;}/*将class为red的div字体大小设置为30px*//*1、交集选择器作用:选中同时复合多…
SAP有用的知识(持续更新)
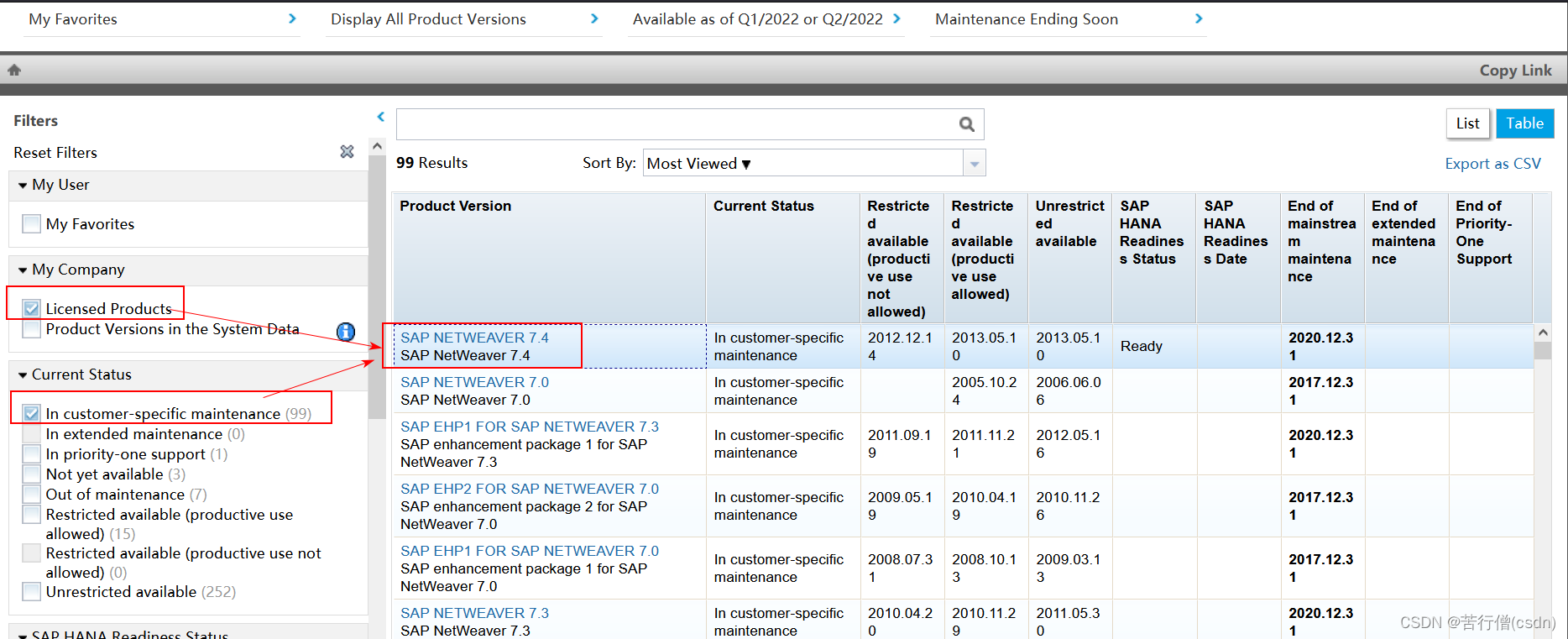
一、安装SAP 1.1、产品可用性矩阵(Product Availability Matrix) SAP官网-Maintenance-Product Availability Matrix,点击页面的Access the Product Availability Matrix。 选中你公司授权的商品(Licensed Products)…
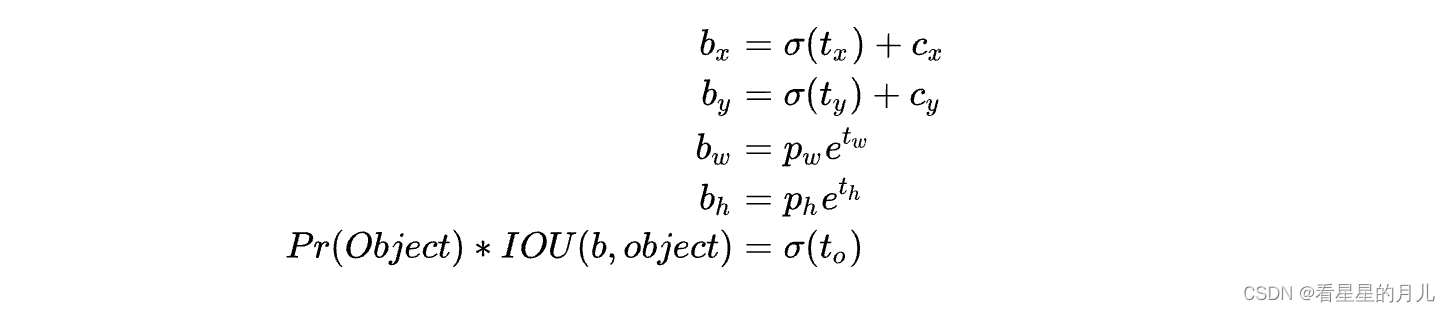
【目标检测】yolo系列:从yolov1到yolov5之YOLOv2详解及复现
YOLO v2 Yolov2论文链接:YOLO9000: Better, Faster, Stronger yolov2的改进 从Yolov2论文的标题可以直观看到就是Better、Faster、Stronger。Yolov1发表之后,计算机视觉领域出现了很多trick,例如批归一化、多尺度训练等等,v2也…

我有一个很好的思维习惯-反思
和我共事过的同事有的会说我聪明,我就暂且当做是夸奖吧,其实我并不是聪明,只是有一个思维习惯。做事过程中或者做完一件事之后会反思这个过程,有哪些地方我是重复操作的,有没有什么地方可以简化流程的,这应…

CSS之关系选择器(子元素、后代、兄弟选择器)
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title></title><style>/*为div的子元素span设置一个字体颜色*//*子元素选择器:作用:选中指定父元素的指定子元素语法:父元素>子…
网络管理员比赛回顾01-基本操作和简单vlan
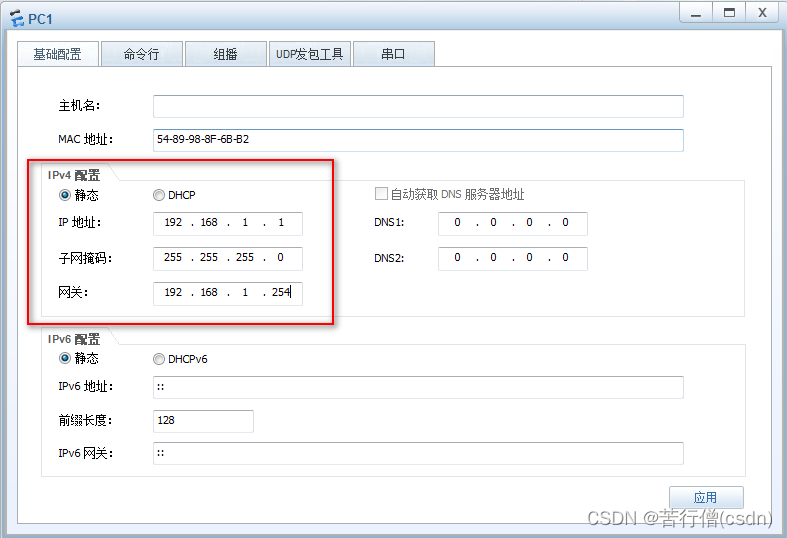
目录 一、模拟器eNSP 二、基本操作 三、配置IP地址 四、VLAN 一、模拟器eNSP 使用eNSP模拟器,来源于网络上的安装包,学习一个。基本操作就不多说了,在实践里慢慢记录 二、基本操作 认识3种视图:用户视图、系统视图、接口视…
【Leetcode】刷题之路3(python版)
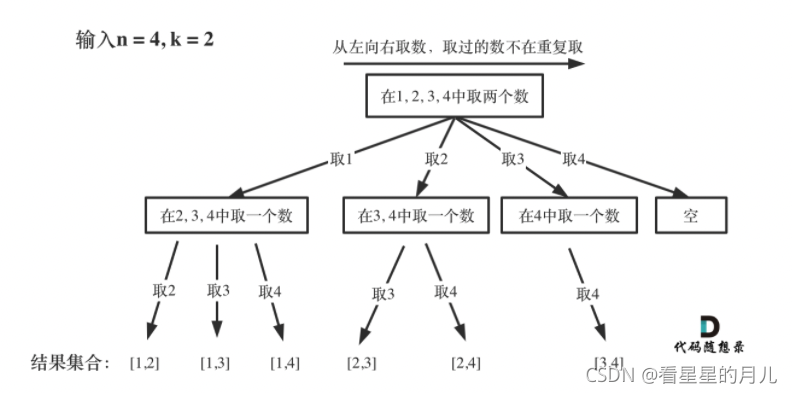
回溯专题 1.回溯算法的本质是n叉树的深度优先搜索,同时,需要注意剪枝减少复杂度。 2.回溯算法三部曲 确定参数和返回值回溯函数终止条件单层循环 3.回溯法思路 回溯法是一种算法思想,而递归是一种编程方法,回溯法可以用递归来…
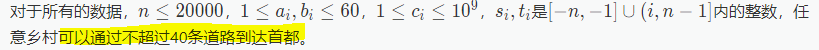
Luogu 4438 [HNOI/AHOI2018]道路
$dp$。 这道题最关键的是这句话: 跳出思维局限大胆设状态,设$f_{x, i, j}$表示从$x$到根要经过$i$条公路,$j$条铁路的代价,那么对于一个叶子结点,有$f_{x, i, j} c_x * (a_x i) * (b_x j)$,对于内部结点…

52深入理解C指针之---不透明指针
该系列文章源于《深入理解C指针》的阅读与理解,由于本人的见识和知识的欠缺可能有误,还望大家批评指教。一、size_t:用于安全表示长度,所有平台和系统都会解析成自己对应的长度 1、定义:size_t类型表示C中任何对…

CSS之布局(文档流)
文档流: <!DOCTYPE html> <html><head><meta charset"utf-8" /><title>文档流</title><style>.box1{background-color: yellow;}</style></head><body><!--文档流(normal fl…
