主成分分析(PCA)Python代码实现
主成分分析(Principal Components Analysis, PCA)简介可以参考: http://blog.csdn.net/fengbingchun/article/details/78977202
这里是参照 http://sebastianraschka.com/Articles/2014_pca_step_by_step.html 文章中的code整理的Python代码,实现过程为:
1. 随机生成3行*40列的数据集,每一列代表一个样本,前20列属于类1,后20列属于类2;每一个样本特征长度为3;
2. 计算每行均值;
3. 计算协方差矩阵,产生一个3行*3列的矩阵;
4. 由协方差矩阵计算特征向量和特征值;
5. 按降序排序特征值和特征向量;
6. 选择第一主成分和第二主成分组成一个新的3行*2列的矩阵;
7. 根据产生的3行*2列矩阵重建原有数据集。
Python代码如下:
# reference: http://sebastianraschka.com/Articles/2014_pca_step_by_step.htmlimport numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
from matplotlib.patches import FancyArrowPatch# 1. generate 40 3-dimensional samples randomly drawn from a multivariate Gaussian distribution
np.random.seed(1) # random seed for consistencymu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20).T
assert class1_sample.shape == (3,20), "The matrix has not the dimensions 3x20"
#print("class1_sample:\n", class1_sample)mu_vec2 = np.array([1,1,1])
cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20).T
assert class2_sample.shape == (3,20), "The matrix has not the dimensions 3x20"fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
plt.rcParams['legend.fontsize'] = 10
ax.plot(class1_sample[0,:], class1_sample[1,:], class1_sample[2,:], 'o', markersize=8, color='blue', alpha=0.5, label='class1')
ax.plot(class2_sample[0,:], class2_sample[1,:], class2_sample[2,:], '^', markersize=8, alpha=0.5, color='red', label='class2')plt.title('Samples for class 1 and class 2')
ax.legend(loc='upper right')
plt.show()# Taking the whole dataset ignoring the class labels
all_samples = np.concatenate((class1_sample, class2_sample), axis=1)
assert all_samples.shape == (3,40), "The matrix has not the dimensions 3x40"# 2. Computing the d-dimensional mean vector
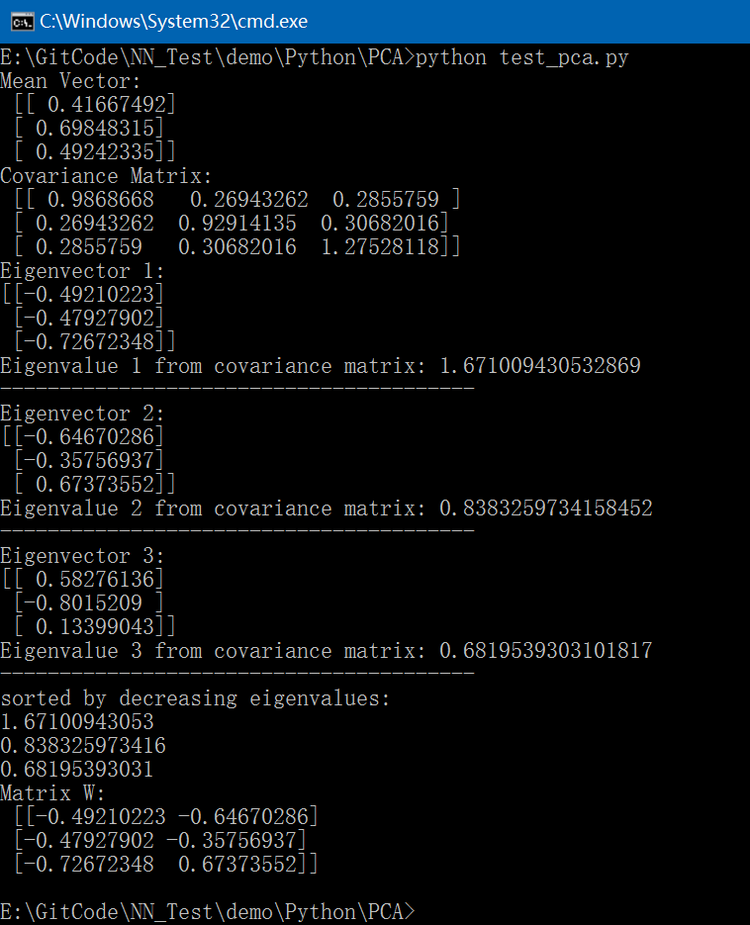
mean_x = np.mean(all_samples[0,:])
mean_y = np.mean(all_samples[1,:])
mean_z = np.mean(all_samples[2,:])mean_vector = np.array([[mean_x],[mean_y],[mean_z]])
print('Mean Vector:\n', mean_vector)# 3. Computing the Covariance Matrix
cov_mat = np.cov([all_samples[0,:],all_samples[1,:],all_samples[2,:]])
print('Covariance Matrix:\n', cov_mat)# 4. Computing eigenvectors and corresponding eigenvalues
eig_val_cov, eig_vec_cov = np.linalg.eig(cov_mat)for i in range(len(eig_val_cov)):eigvec_cov = eig_vec_cov[:,i].reshape(1,3).Tprint('Eigenvector {}: \n{}'.format(i+1, eigvec_cov))print('Eigenvalue {} from covariance matrix: {}'.format(i+1, eig_val_cov[i]))print(40 * '-')# Visualizing the eigenvectors
class Arrow3D(FancyArrowPatch):def __init__(self, xs, ys, zs, *args, **kwargs):FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)self._verts3d = xs, ys, zsdef draw(self, renderer):xs3d, ys3d, zs3d = self._verts3dxs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))FancyArrowPatch.draw(self, renderer)fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')ax.plot(all_samples[0,:], all_samples[1,:], all_samples[2,:], 'o', markersize=8, color='green', alpha=0.2)
ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5)
for v in eig_vec_cov.T:a = Arrow3D([mean_x, v[0]], [mean_y, v[1]], [mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r")ax.add_artist(a)
ax.set_xlabel('x_values')
ax.set_ylabel('y_values')
ax.set_zlabel('z_values')plt.title('Eigenvectors')
plt.show()# 5 Sorting the eigenvectors by decreasing eigenvalues
# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_val_cov[i]), eig_vec_cov[:,i]) for i in range(len(eig_val_cov))]# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
print("eig_pairs:\n", eig_pairs)# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print("sorted by decreasing eigenvalues:")
for i in eig_pairs:print(i[0])# 6 Choosing k eigenvectors with the largest eigenvalues
matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1)))
print('Matrix W:\n', matrix_w)# 7 Transforming the samples onto the new subspace
transformed = matrix_w.T.dot(all_samples)
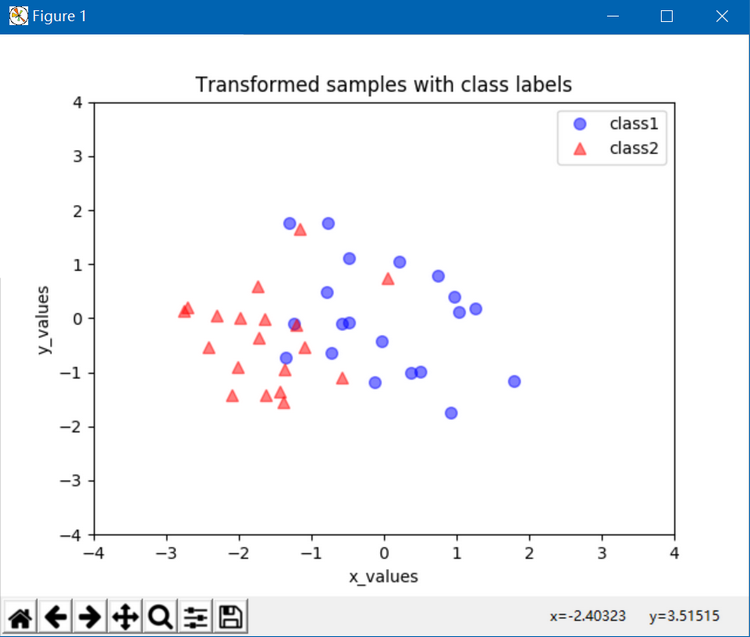
assert transformed.shape == (2,40), "The matrix is not 2x40 dimensional."plt.plot(transformed[0,0:20], transformed[1,0:20], 'o', markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(transformed[0,20:40], transformed[1,20:40], '^', markersize=7, color='red', alpha=0.5, label='class2')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.legend()
plt.title('Transformed samples with class labels')
plt.show()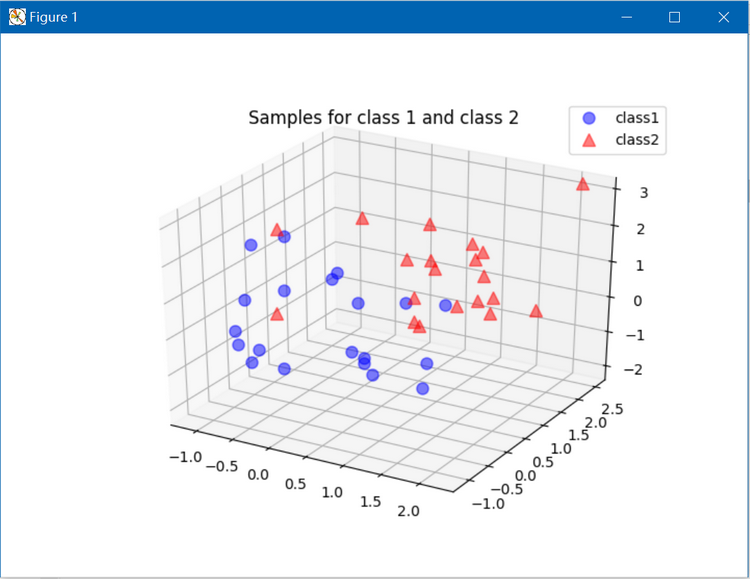
相关文章:

AI发展这一年:不断衍生的技术丑闻与抵制声潮
作者 | AI Now学院译者 | Raku编辑 | Jane出品 | AI科技大本营(ID: rgznai100)【导读】10月2日,纽约大学AI Now学院在纽约大学斯克博剧院(Skirball Theatre)组织召开了第四届年度AI Now研讨会。研讨会邀请了业内组织者…

Distributed Configuration Management Platform(分布式配置管理平台)
2019独角兽企业重金招聘Python工程师标准>>> 专注于各种 分布式系统配置管理 的通用组件/通用平台, 提供统一的配置管理服务。 主要目标: 部署极其简单:同一个上线包,无须改动配置,即可在 多个环境中(RD/QA/PRODUCTION…

如何利用zendstudio新建 或导入php项目
为什么80%的码农都做不了架构师?>>> 一、利用ZendStudio创建 PHP Project 1. 打开ZendStudio, 选择:File à New à PHP Project, 如下图所示: 于是弹出如下界面: 在”Project name”后输入工程名(比如我这里…

一文读懂GoogLeNet神经网络 | CSDN博文精选
作者 | .NY&XX来源 | CSDN博客本文介绍的是著名的网络结构GoogLeNet,目的是试图领会其中结构设计思想。GoogLeNet特点优化网络质量的生物学原理GoogLeNet网络结构的动机GoogLeNet架构细节Inception模块和普通卷积结构的差异辅助分类器GoogLeNet网络架构GoogLeNe…

C++中的函数签名
C中的函数签名(function signature):包含了一个函数的信息,包括函数名、参数类型、参数个数、顺序以及它所在的类和命名空间。普通函数签名并不包含函数返回值部分,如果两个函数仅仅只有函数返回值不同,那么系统是无法区分这两个函…

MyEclipse断点调试
2019独角兽企业重金招聘Python工程师标准>>> 1、在编辑的程序的左边,你会看到一条浅浅的灰色编带,在这里设置断点。 2、设置断点的方法有很多 方法:1)、双击 ; 2)、右键,选择“Toggl…

C primer plus 练习题 第三章
5. 1 #include <stdio.h>2 3 int main()4 {5 float you_sec;6 printf("请输入你的年龄:");7 scanf("%f", &you_sec);8 printf("年龄合计:%e 秒!\n", you_sec * 3.156e7);9 getchar(); 10 return 0; 11 }

Echache整合Spring缓存实例讲解
2019独角兽企业重金招聘Python工程师标准>>> 摘要:本文主要介绍了EhCache,并通过整合Spring给出了一个使用实例。 一、EhCache 介绍 EhCache 是一个纯Java的进程内缓存框架,具有快速、精干等特点,是Hibernate中默认的C…
灰度图像直方图均衡化公式及实现
图像的直方图:直方图是图像中像素强度分布的图形表达方式。它统计了每一个强度值所具有的像素个数。直方图均衡化:是通过拉伸像素强度分布范围来增强图像对比度的一种方法。是图像处理领域中利用图像直方图对对比度进行调整的方法。均衡化指的是把一个分…
超越最新无监督域自适应方法,研究人员提轻量CNN新架构OSNet
作者 | Kaiyang Zhou, Xiatian Zhu, Yongxin Yang, Andrea Cavallaro, and Tao Xiang 译者 | TroyChang 编辑 | Jane 出品 | AI科技大本营(ID:rgznai100) CNN新架构OSNet 【导读】今天推荐论文《Learning Generalisable Omni-Scale Repre…

在一台机器上搭建多个redis实例
2019独角兽企业重金招聘Python工程师标准>>> 默认Redis程序安装在/usr/local/redis目录下; 配置文件:/usr/local/redis/redis.conf,该配置文件中配置的端口为默认端口:6379; Redis的启动命令路径࿱…

使用kaptcha生成验证码
2019独角兽企业重金招聘Python工程师标准>>> kaptcha是一个简单好用的验证码生成工具,通过配置,可以自己定义验证码大小、颜色、显示的字符等等。下面就来讲一下如何使用kaptcha生成验证码以及在服务器端取出验证码进行校验。 一、搭建测试环…

主成分分析(PCA) C++ 实现
主成分分析(Principal Components Analysis, PCA)简介可以参考: http://blog.csdn.net/fengbingchun/article/details/78977202以下是PCA的C实现,参考OpenCV 3.3中的cv::PCA类。使用ORL Faces Database作为测试图像。关于ORL Faces Database的介绍可以参…

为何Google、微软、华为将亿级源代码放一个仓库?从全球最大代码管理库说起...
作者 | 夕颜编辑 | Just出品 | AI 科技大本营(ID:rgznai100)【导读】2017 年,在当时微软的一篇官方博客中,时任微软云开发服务副总裁的 Brian Harry 表示微软内部代码开始向 Git 迁移,宣布推出针对大规模 repo 的“Git…

jquery mobie导致超链接不可用
在a标签中添加rel"external"即可转载于:https://blog.51cto.com/here2142/1435434

编译器GCC与Clang的异同
GCC:GNU(Gnus Not Unix)编译器套装(GNU Compiler Collection,GCC),指一套编程语言编译器,以GPL及LGPL许可证所发行的自由软件,也是GNU项目的关键部分,也是GNU工具链的主要组成部分之一。GCC(特别是其中的C语…

如何正确选择聚类算法? | CSDN博文精选
作者 | Josh Thompson翻译 | 张睿毅校对 | 王雨桐来源 | 数据派THU(ID:DatapiTHU)本文将介绍四种基本的聚类算法—层次聚类、基于质心的聚类、最大期望算法和基于密度的聚类算法,并讨论不同算法的优缺点。聚类算法十分容易上手,但…

Python工具 | 9个用来爬取网络站点的 Python 库
1️⃣Scrapy 一个开源和协作框架,用于从网站中提取所需的数据。 以快速,简单,可扩展的方式。 官网2️⃣cola 一个分布式爬虫框架。 GitHub3️⃣Demiurge 基于 PyQuery 的爬虫微型框架。 官网4️⃣feedparser 通用 feed 解析器。 官网5️⃣Gra…

Python并发编程实例教程
有关Python中的并发编程实例,主要是对Threading模块的应用,文中自定义了一个Threading类库。 一、简介 我们将一个正在运行的程序称为进程。每个进程都有它自己的系统状态,包含内存状态、打开文件列表、追踪指令执行情况的程序指针以及一个保存局部变量的调用栈。…
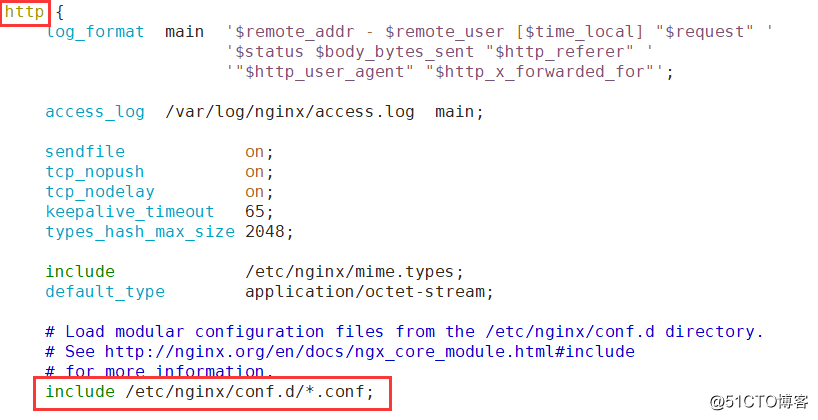
Nginx负载均衡之TCP端口高可用(二)
在前面我们实现了基本的HTTP反向代理,从互联网过来的请求已经可以分发到后端多台网站服务器上,但不是所有的业务都是网络类型的,此篇文章我们主要讨论的是TCP 端口的负载均衡做法,昨天也有小伙伴提到了,在HTTP反向代理…

语音识别大牛Daniel Povey为何加入小米?“手机+AIoT”强大生态,开源战略是关键...
整理 | 夕颜出品 | AI科技大本营(ID:rgznai100)10 月 17 日,语音识别开源工具 Kaldi 创始人,语音和 AI 领域大牛 Daniel Povey 在10 月 19 日,小米集团副总裁、集团技术委员会主席崔宝秋发布微博,欢迎 Dani…

Python运维项目中用到的redis经验及数据类型
先感叹下,学东西一定要活学活用! 我用redis也有几年的历史了,今个才想到把集合可以当python list用。 最近做了几个项目都掺杂了redis, 遇到了一些个问题和开发中提高性能的方法,这都分享出来,共同学习。…
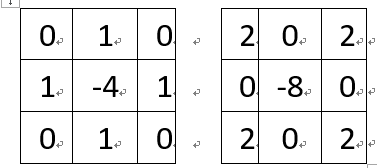
图像边缘检测之拉普拉斯(Laplacian)C++实现
拉普拉斯算子(Laplacian)可应用到图像边缘检测中。在OpenCV中当kernel大小为3*3时,支持两种kernel算子,分别为:在OpenCV中默认的计算方式如下,假设有一个5*5的小图像,原始值依次为1,2,…25,如下图红色部分,…

从0到1,Airbnb的深度学习实践经验总结
作者 | Haldar译者 | 陆离出品 | AI科技大本营(ID: rgznai100)此前,AI科技大本营发布了关于希望通过介绍的研究成果为读者提供一些有用的帮助和指引。模型中的生态系统本文要讨论的机器学习现实应用,是关于根据用户预约的可能性来…

高并发大流量专题---8、动态语言的并发处理
高并发大流量专题---8、动态语言的并发处理 一、总结 一句话总结: 和本科毕业论文连起来了:基于消息中间件Rocket MQ的研究;用于并发处理的消息队列 1、什么是进程、线程、协程? 进程(Process)是计算机中的…

1. 文件系统——磁盘分区、各目录功能、硬盘
一、磁盘分区及文件访问入口在前文中介绍过,Linux的整个文件系统像一棵倒置的数,最顶层的是根文件系统,其下有很多一级子目录,一级子目录下面是二级子目录,依此类推:/:根目录/bin,/s…

吴恩达老师深度学习视频课笔记:逻辑回归公式推导及C++实现
逻辑回归(Logistic Regression)是一个二分分类算法。逻辑回归的目标是最小化其预测与训练数据之间的误差。为了训练逻辑回归模型中的参数w和b,需要定义一个成本函数(cost function)。成本函数(cost function):它是针对整个训练集的。衡量参数w和b在整个训…

网络运行时间提高100倍,Google使用的AI视频理解架构有多强?
译者 | 刘畅出品 | AI科技大本营(ID:rgznai100)视频理解是一个很有挑战性的问题。由于视频包含时空数据,因此图像的特征表示需要同时提取图像和运动信息。这不仅对自动理解视频语义内容有重要性,还对机器人的感知和学习也至关重要…

iOS学习笔记(十三)——获取手机信息(UIDevice、NSBundle、NSLocale)
2019独角兽企业重金招聘Python工程师标准>>> iOS的APP的应用开发的过程中,有时为了bug跟踪或者获取用反馈的需要自动收集用户设备、系统信息、应用信息等等,这些信息方便开发者诊断问题,当然这些信息是用户的非隐私信息࿰…

吴恩达老师深度学习视频课笔记:单隐含层神经网络公式推导及C++实现(二分类)
关于逻辑回归的公式推导和实现可以参考: http://blog.csdn.net/fengbingchun/article/details/79346691 下面是在逻辑回归的基础上,对单隐含层的神经网络进行公式推导:选择激活函数时的一些经验:不同层的激活函数可以不一样。如果…
