90 后 CTO 创业 6 年,做了一件改变互联网的“小事”
TGO 鲲鹏会在武汉举行了一场线下分享活动 —— 冲破壁垒,打造精英的技术团队 。来自极验的 90 后 CTO 黄胜蓝分享了他的团队故事,以及在他看来一个创新团队应该具备的特征。

1. 创新:非典型性切入
黄胜蓝笑称自己只有高中学历,2012 年,还在上大三的他,决定出来和另外两位创始人一起创业。就这样,“三剑客”团队带着初生牛犊不怕虎的闯劲,在武大旁边租了一间宿舍大小的民宅,开始了他们的创业之旅。那时,他们连 2B 的概念都弄不清,更不用说具体的编程语言,只能从大众公开的信息中提取加工。
当时,很多网站或者互联网产品在运营的时候,资源经常会被黑客窃取,极验想解决这个问题。而主要解决方式是,通过阻断短信验证码自动解码,避免大量的运营资源被拿走,也就是提供一站式交互安全解决方案,抵御恶意攻击,保护企业资产。
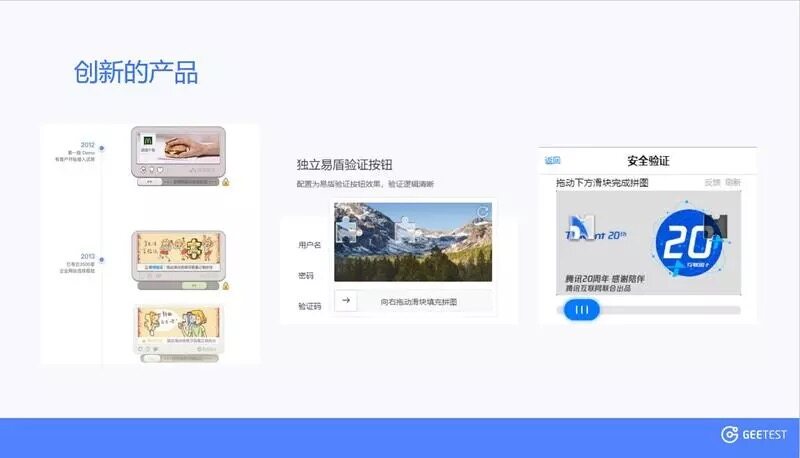
在 2012 年底,他们变革掉了此前一直在用的图形验证码,首创了“行为式验证”,具体的产品形式,就是演变为一个小小的滑动验证。2013 年,他们拥有了第一个客户。从游戏和媒体行业开始突破,到后面的航空公司,慢慢地肯德基、小米、微博也都成为了他们的客户。如今,极验这个团队已经给二十多万家客户、四五百家付费客户提供服务,每天能提供 8 亿左右的验证次数。
他说:“大家都见过我们的产品,只是不知道我们公司而已。我们花了 6 年时间,做了改变互联网或者改变世界的一件小事。”
2. 创新:团队需要具备三个特性
2.1 创新团队 = 极致 + 突破 + 相信

在黄胜蓝看来,自己的团队是一个敢于创新的团队。结合 6 年的创业经验,他总结出创新的团队需要具备三个特性:
第一个是极致,整个公司的产品形式需要做到极致;
第二个是勇于突破,不要太过关注业界领先者是什么样,而应该把更多的时间留给自己,关注自己能不能做到更好;
第三个是相信自己,在公司创业初期,都是一群没有社会和工作经验的年轻人,当时主要的技术成员差不多是大三的水平,这就是为什么要相信自己。
2.2 驱动企业技术创新的三架马车:安全性、稳定性、性能
除了大的产品形式,黄胜蓝也分享了驱动企业技术创新的三架马车,那就是安全性、稳定性和性能。
第一是安全性。需要你不断地提升验证的安全性,让程序和自动脚本没有办法通过;对正常的操作,则是保证很好的用户体验。这就需要不断地深挖这个过程,为客户提供核心价值。
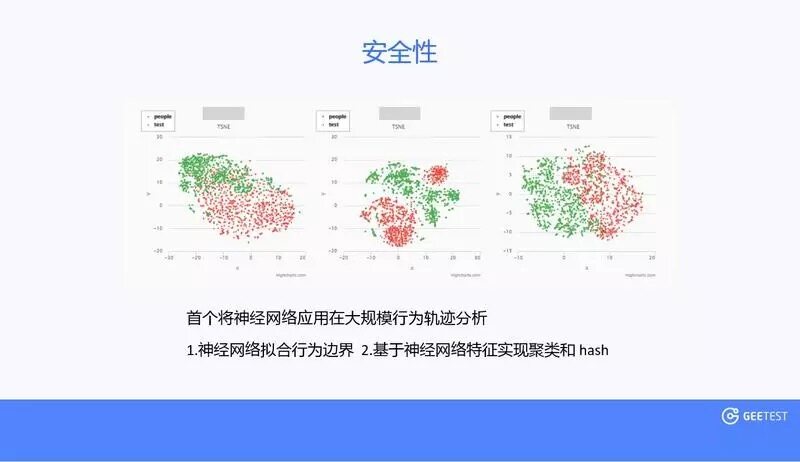
滑动的过程中需要采集鼠标和触屏的轨迹,早在 2013 年没有人做过这个事情。当时,极验团队引入了神经网络,利用神经网络拟合人和机器的行为边界。比如,用户在使用鼠标拖动拼图拼合的过程中,受限于鼠标和人的肌肉结构,动作做出来要符合人的特性,人的特性就是用神经网络去做的。在图中红色部分就是人,把利用神经网络、分类网络提取的特征可视化,这就是安全性的体现。此外,基于神经网络利用分类网络做分类器,就是解决某些脚本攻击的行为特征,这也是滑动验证的安全性的一种体现。
第二是稳定性。稳定性非常重要,验证码是在登录注册的位置,稳定性有问题的话,所有流程都无法使用,新用户也会注册不了。稳定性是需要投入大量精力进行大量创新的地方。

在不断迭代的过程中,为了保证产品的安全性,极验团队内部开发了一个自研分布式 Redis。实践之后,达到了零故障恢复时间的效果。此外也减少了中间组件。如果采用代理形式的话而不靠自主研发,不但要监控客户端,还要监控代理层,这样的操作会十分麻烦。
第三是性能,每一个验证过程都会涉及到大量的计算,性能代表了两个方向,一是单次验证尽可能快地返回;二是涉及到成本,性能优化做得越好,成本就越低。
举个例子,每次的验证图片都是不重复的,消耗量非常大,就会导致生成这个图片的成本特别高。而黄胜蓝带着技术团队做了优化,每秒可以跑 2000 多张。就是这样一个看起来很简单的事情,在背后他们也做了大量优化和创新。
再比如团队对神经网络的优化,每一个验证要一个神经网络去预测。而当时的情况是没有 GPU 用,于是,团队就把就把 CPU 做得很深。具体来说,就是利用了 CPU 指令集优化来做实现,把一个在 CPU 上跑的神经网络优化到了只要七八毫秒。
这就是产品形式留给技术团队的三个攻关的方向,这三个点就构成了技术创新的三架马车。
3.Q\u0026amp;A
当时研发出的产品是怎么测试的?
安全类的产品很难讲是否保证 100% 安全,黑客也会不断进化,我们更多的是去说服别人相信这个东西更安全。比如说服他们,传统的图形肯定是不安全的。同时,利用其他客户的案例,大量的客户在使用了产品后基本上解决了业务安全问题,如果部分客户仍然出现问题,我们会用模型的更新去解决。我们没有办法保证这个用了以后就高枕无忧了,实际上任何产品都不能保证,但是我们能提供一个更先进的战场,可以帮助企业战胜黑客。
你们的产品还是沿用你们当时开发的这些模型?
一直都在改进。另外还包括数据存储的集群、集群调度的系统。在神经网络执行方面,我们内部做了调度系统,以任务的形式去提交,自动准备数据。本质上,我们所做的东西也没有什么区别,只是我们做得更早而已。落地的话,是靠整个团队和系统,没有短板才能把神经网络在业务领域做一个很好的应用,这个东西才能做得更扎实。
你刚开始创业的时候,是把整个的技术归纳布局好,还是边试错边做的?
回答肯定是后者。我当时是高中学历,很多东西对我来说都是前沿的。就算当时布局好了,后面就不会有新的东西出来了吗?要做创新,很重要的一点就是相信自己,赶紧去做,然后随机应变。不要固守自己之前做的东西,觉得有必要的就去做,不要去管是否处在业界领先。
公司遇到新技术时,有很完善的技术团队去分布地学习?还是就靠你一个人?
不是靠一个人,是靠一个理念。理念要灌输下去,使团队成员不断地学习,随机应变,不固守以前的东西。
TGO鲲鹏会,系极客邦科技旗下高端技术人聚集和交流的组织,旨在组建全球最具影响力的科技领导者社交网络,线上线下相结合,为会员提供专享服务。目前,TGO鲲鹏会已在北京、上海、杭州、广州、深圳、成都、硅谷、台湾、南京、厦门、苏州十一个城市设立分会,武汉分会即将成立。现在全球拥有在册会员 740 余名,60% 为 CTO、技术 VP、技术合伙人。
会员覆盖了 BATJ 等互联网巨头公司技术领导者,同时,阿里巴巴王坚博士、同程艺龙技术委员会主任张海龙、苏宁易购 IT 总部执行副总裁乔新亮已经受邀,成为 TGO 鲲鹏会荣誉导师。
如果你想和这些优秀的科技领导者们一起前行,欢迎点击「报名表单,申请加入」。
相关文章:
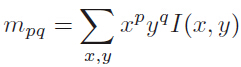
ORB特征(二)
为了满足实时性的要求,前面文章中介绍过(具体链接如下)快速提取特征点算法Fast,以及特征描述子Brief。本篇文章介绍的ORB算法结合了Fast和Brief的速度优势,并做了改进,且ORB是免费Ethan Rublee等人2011年在《ORB&#…

【POJ】2377 Bad Cowtractors(最大生成树)
简单题,模板题 求解最大生成树,提交一直WA,感觉没有什么问题啊,就是在求解最小生成树的模板基础上稍加修改即可,后来发现在输出a,b,c给map二维数组的时候还必须有判断条件,略为有点…

使用let替换var实现块级作用域的小发现
在讲述javascript没有块级作用域的时候都会提到一个非常经典的例子: var obj{name:helo,age:15 }; var arr[];for(var i0;i<5;i){arr[i]i;console.log(i);} console.log(arr); console.log(i);因为javascript没有块级作用域,所以控制台打印出来的结果…

windows系统下node、npm的安装和卸载
Greta有话说:我是在有道云笔记只弄个记录的笔记,粘贴过来之后,没有图片,我的笔记地址为: 有道云笔记,请点我 一、卸载 1、node.js、nvm、 npm (1)在cmd中输入where node找到node…
OpenCV4Android开发实录(2): 使用OpenCV3.4.1库实现人脸检测
OpenCV4Android开发实录(2): 使用OpenCV3.3.0库实现人脸检测 转载请声明出处:http://write.blog.csdn.net/postedit/78992490OpenCV4Android系列: 1. OpenCV4Android开发实录(1):移植OpenCV3.3.0库到Android Studio 2.OpenCV4Andr…

活动|跟着微软一起,拥抱开源吧!
由开源社主办的中国开源年会2016 (COSCon16 - China Open Source Conference 2016) 即将于今年10月15日-16日在北京举办。微软大咖将为您呈现区块链,容器,大数据,Xamarin等时下热点技术,参会者还可获取价值1,500 元 Azure 服务使用…

【HDU/算法】最短路问题 杭电OJ 2544 (Dijkstra,Dijkstra+priority_queue,Floyd,Bellman_ford,SPFA)
最短路径问题是图论中很重要的问题。 解决最短路径几个经典的算法 1、Dijkstra算法 单源最短路径(贪心),还有用 priority_queue 进行优化的 Dijkstra 算法。 2、bellman-ford算法 例题:【ACM】POJ 3259 Wormholes 允许负权边…

javaSE基础知识 1.5整数类型
整数的四种声明类型它们分别是,byte,short,int,long,这四种类型所占用的空间是不同的byte是占用1个字节,它的取值范围是 -128~127,short是占用2个字节,他的取值范围是-32768~32767&a…

源码分析-GLSurfaceView的内部实现
GLSurfaceView类是继承自SurfaceView的,并且实现了SurfaceHolder.Callback2接口。GLSurfaceView内部管理着一个surface,专门负责OpenGL渲染。GLSurfaceView内部通过GLThread和EGLHelper为我们完成了EGL环境渲染和渲染线程的创建及管理,使我们…

【POJ/算法】 3259 Wormholes(Bellman-Ford算法, SPFA ,FLoyd算法)
Bellman-Ford算法 Bellman-Ford算法的优点是可以发现负圈,缺点是时间复杂度比Dijkstra算法高。而SPFA算法是使用队列优化的Bellman-Ford版本,其在时间复杂度和编程难度上都比其他算法有优势。 Bellman-Ford算法流程分为三个阶段: 第一步&am…
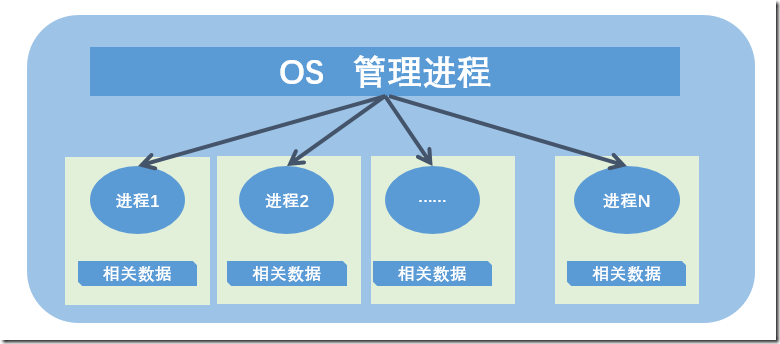
进程控制概念简介 多线程上篇(三)
进程控制 进程的基本数据信息是操作系统控制管理进程的数据集合,这些信息就是用来控制进程的,此处我们说的进程控制就是进程的管理。比如进程有状态,那么进程的创建、终止,状态的切换,这都不是进程自主进行的ÿ…

Android OpenGL使用GLSurfaceView预览视频
Android OpenGL使用GLSurfaceView预览视频第一章 相关知识介绍在介绍具体的功能之前,先对一些主要的类和方法进行一些介绍,这样可以更好的理解整个程序1.1 GLSurfaceView在谷歌的官方文档中是这样解释GLSurfaceView的:An implementation of S…

【Android 基础】Animation 动画介绍和实现
转载自:http://www.cnblogs.com/yc-755909659/p/4290114.html1.Animation 动画类型Android的animation由四种类型组成:XML中alph渐变透明度动画效果scale渐变尺寸伸缩动画效果translate画面转换位置移动动画效果rotate画面转移旋转动画效果JavaCode中Alp…

【Codeforces】1111B - Average Superhero Gang Power
http://codeforces.com/problemset/problem/1111/B n 表示要输入的数据的个数 k 最每一个数据最多可以进行多少次操作 m 一共可以进行多少次操作 一次操作:删除这个数,或者给这个数加1 如果n为1的话,那么只要找出m和k的最小值加到那个数…

刷前端面经笔记(七)
1.描述一下渐进增强和优雅降级 优雅降级(graceful degradation):一开始就构建站点的完整功能,然后针对浏览器测试和修复。渐进增强(progressive enhancement):一开始只构建站点的最少特性,然后不断针对各浏览器追加功能。 2.为什么…

AR资料与连接梳理
AR引擎相关技术 ------------------------------ ARcore:https://developers.google.cn/ar/discover/ ARkit:https://developer.apple.com/arkit/ 以上重点关注,比较新有一些新的功能大家可以自行体验。 ARToolkithttp://www.artoolkit.orght…

Queues 队列
1. Definiation What is a queue? A queue is a list. With a queue, inseration is done at one end (known as rear) whereas deletion is performed at the other end (known as front). 2. Operations 指针对列 无法自定义队长 // array queue #include<iostream> u…

【HDU】1005 Number Sequence (有点可爱)
http://acm.hdu.edu.cn/showproblem.php?pid1005 A number sequence is defined as follows: f(1) 1, f(2) 1, f(n) (A * f(n - 1) B * f(n - 2)) mod 7. Given A, B, and n, you are to calculate the value of f(n). 直接递归求解f(n)的话,会MLE 在计算…

CNCF案例研究:奇虎360
公司:奇虎360地点:中国北京行业:计算机软件 挑战 中国软件巨头奇虎360科技的搜索部门,so.com是中国第二大搜索引擎,市场份额超过35%。该公司一直在使用传统的手动操作来部署环境,随着项目数量的…

C#代码实现对Windows凭据的管理
今天有个任务,那就是使用C#代码实现对windows凭据管理的操作。例如:向windows凭据管理中添加凭据、删除凭据以及查询凭据等功能。于是乎,就开始在网上查找。经过漫长的查询路,终于在一片英文博客中找到了相关代码。经过实验&#…

Android:JNI 与 NDK到底是什么
前言 在Android开发中,使用 NDK开发的需求正逐渐增大但很多人却搞不懂 JNI 与 NDK 到底是怎么回事今天,我将先介绍JNI 与 NDK & 之间的区别,手把手进行 NDK的使用教学,希望你们会喜欢 目录 1. JNI介绍 1.1 简介 定义&…
【ACM】LightOJ - 1008 Fibsieve`s Fantabulous Birthday (找规律,找...)
https://vjudge.net/problem/LightOJ-1008 题目很好理解,第一行表示测试样例的个数,接下来输入一个大于等于1的数,按照格式输出这个数的坐标 蓝色的是 奇数的平方; 红色的是 偶数的平方; 黄色的是对角线:…

Computed property XXX was assigned to but it has no setter
报错视图: 原因: 组件中v-model“XXX”,而XXX是vuex state中的某个变量vuex中是单项流,v-model是vue中的双向绑定,但是在computed中只通过get获取参数值,没有set无法改变参数值解决方法: 1.在co…

OpenGL 矩阵变换
origin refer :http://www.songho.ca/opengl/gl_transform.html#modelviewOpenGL 矩阵变换Related Topics: OpenGL Pipeline, OpenGL Projection Matrix, OpenGL Matrix Class Download: matrixModelView.zip, matrixProjection.zipOverviewOpenGL Transform MatrixExample: GL…

2016.8.11 DataTable合并及排除重复方法
合并: DataTable prosxxx; DataTable pstaryyy; //将两张DataTable合成一张 foreach (DataRow dr in pstar.Rows) { pros.ImportRow(dr); } DataTable设置主键,并判断重复 DataTable allpros xxx; 单列设为主键: //设置第某列为主键 allpros.…
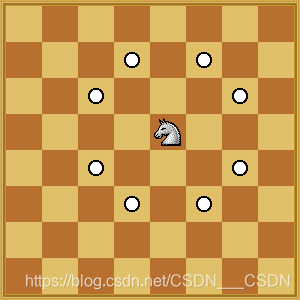
【ACM】LightOJ - 1010 Knights in Chessboard(不是搜索...)
https://vjudge.net/problem/LightOJ-1010 给定一个mn的棋盘,你想把棋子放在哪里。你必须找到棋盘上最多可以放置的骑士数量,这样就不会有两个骑士互相攻击。不熟悉棋手的注意,棋手可以在棋盘上攻击8个位置,如下图所示。 不论输入…

webpack-dev-server 和webapck --watch的区别
webpack-dev-server 和webapck --watch 都可以监测到代码变化 , 区别是:webpack-der-server 监测到代码变化后,浏览器可以看到及时更新的效果,但是并没有自动打包修改的代码; webpack --watch 在监测到代码变化后自动打…
Android 应用进行性能分析/APP/系统性能分析
如何对 Android 应用进行性能分析记录一下自己在使用DDMS的过程:开启AS,打开并运行项目 找到TOOL/选择Android Device Monitor一款 App 流畅与否安装在自己的真机里,玩几天就能有个大概的感性认识。不过通过专业的分析工具可以使我们更好的分…

公钥与私钥,HTTPS详解
1.公钥与私钥原理1)鲍勃有两把钥匙,一把是公钥,另一把是私钥2)鲍勃把公钥送给他的朋友们----帕蒂、道格、苏珊----每人一把。3)苏珊要给鲍勃写一封保密的信。她写完后用鲍勃的公钥加密,就可以达到保密的效果。4)鲍勃收信后,用私钥…

【ACM】杭电OJ 4704 Sum (隔板原理+组合数求和公式+费马小定理+快速幂)
http://acm.hdu.edu.cn/showproblem.php?pid4704 1.隔板原理 1~N有N个元素,每个元素代表一个1.分成K个数,即在(N-1)个空挡里放置(K-1)块隔板 即求组合数C(N-1,0)C(N-1,1)...C(N-1,N-1) 2.组合数求和公式 C(n,0)C(…
