【POJ/算法】 3259 Wormholes(Bellman-Ford算法, SPFA ,FLoyd算法)
Bellman-Ford算法
Bellman-Ford算法的优点是可以发现负圈,缺点是时间复杂度比Dijkstra算法高。而SPFA算法是使用队列优化的Bellman-Ford版本,其在时间复杂度和编程难度上都比其他算法有优势。
Bellman-Ford算法流程分为三个阶段:
第一步:数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为INF, Distant[s]为0;
第二步:以下操作循环执行至多n-1次,n为顶点数: 对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值; 若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。否则执行下次循环;
第三步:为了检测图中是否存在负环路,即权值之和小于0的环路。对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
v的最短距离保存在 d[v]中。
在这个算法中,需要了解的几点
1、只有上一次迭代中松驰过的点才有可能参与下一次迭代的松弛操作。
似乎算法在遍历每一条边的做法会浪费时间,或许我们只需要考虑那些被成功松弛的点的邻点就可以了。我们可以用一个队列来维护这些被成功松弛的点,这个小小的改进可以节省很多时间,改进后的算法叫做SPFA。
2、迭代的实际意义:每一次迭代k中,我们找到了经历了k条边的最短路
3、没有点能够松弛时,迭代结束
Bellman-Ford(G,w,s) :boolean //图G ,边集 函数 w ,s为源点for each vertex v ∈ V(G) do //初始化 1阶段d[v] ←+∞d[s] ←0; //1阶段结束for i=1 to |v|-1 do //2阶段开始,双重循环。for each edge(u,v) ∈E(G) do //边集数组要用到,穷举每条边。If d[v]> d[u]+ w(u,v) then //松弛判断d[v]=d[u]+w(u,v) //松弛操作 2阶段结束for each edge(u,v) ∈E(G) doIf d[v]> d[u]+ w(u,v) thenExit falseExit true
SPFA
算法特点:在 Bellman-ford 算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
关键词:初始化,relax,队列
实现的过程和Bellman_Ford类似
【初始化】
dis数组全部赋值为INF,pre数组全部赋值为-1(表示还不知道前驱),
dis[s] = 0 表示源点不要求最短路径(或者最短路径就是0)。
【队列+松弛操作】
读取队头顶点u,并将队头顶点u出队(记得消除标记);将与点u相连的所有点v进行松弛操作,如果能更新估计值(即令d[v]变小),那么就更新,另外,如果点v没有在队列中,那么要将点v入队(记得标记),如果已经在队列中了,那么就不用入队,这样不断从队列中取出顶点来进行松弛操作。
以此循环,直到队空为止就完成了单源最短路的求解。
【算法过程】
设立一个队列用来保存待优化的顶点,优化时每次取出队首顶点 u,并且用 u 点当前的最短路径估计值dis[u]对与 u 点邻接的顶点 v 进行松弛操作,如果 v 点的最短路径估计值dis[v]可以更小,且 v 点不在当前的队列中,就将 v 点放入队尾。这样不断从队列中取出顶点来进行松弛操作,直至队列空为止。
【检测负权回路】
方法:如果某个点进入队列的次数大于等于 n,则存在负权回路,其中 n 为图的顶点数。
#include <iostream>
#include <queue>
#include <stack>
#include <cstring>
#include <cstdio>
#include <functional>
using namespace std;const int maxn = 99999999;
int map[205][205];//邻接矩阵
int d[205];//源点到顶点i的最短距离
bool vis[205];//标记数组
int enqueue_num[205];//记录入队次数
int path[205];//记录最短的路径
int n;//顶点数
int e;//边数
int start;//源点bool SPFA()
{memset(vis,false,sizeof(vis));memset(enqueue_num,0,sizeof(enqueue_num));for(int i=0;i<n;i++){d[i] = maxn;path[i] = start;}queue<int> Q;Q.push(start);d[start] = 0;vis[start] = 1;enqueue_num[start]++;int v;while(Q.empty()!=1){int u = Q.front();Q.pop();vis[u] = 0;for(v=0;v<n;v++){if(map[u][v]!=maxn)//u 与 v 直接邻接{if(d[u]+map[u][v]<d[v]){d[v] = d[u] + map[u][v];path[v] = u;if(!vis[v]){Q.push(v);enqueue_num[v]++;if(enqueue_num[v]>=n){return false;}vis[v] = true;}}}}}return true;
}void print()
{int i;for(i=0;i<n;i++){if(i!=start){int p = i;stack<int> s;cout << "顶点 " << start << " 到顶点 " << p << "最短路是:";while(start!=p){s.push(p);p=path[p];}cout << start;while(s.empty()!=1){cout << "---" << s.top();s.pop();}cout << " 最短路径的长度是:" << d[i] << endl; }}
}int main()
{int i, j;cout << "请输入图的顶点数,边数,源点:\n";cin >> n >> e >> start;//初始化for(i=0;i<=n;i++){for(j=0;j<=n;j++){if(i==j) map[i][j] = 0;else map[i][j] = maxn;}}cout << "请输入" << e << "条边的信息:\n";int u, v, w;//默认是有向图for(i=0;i<e;i++){cin >> u >> v >> w;map[u][v] = w;}if(SPFA())print();elsecout << "Sorry,it has negative circle!\n";return 0;
}用下面这张图进行测试数据:

现学现用
http://poj.org/problem?id=3259
【问题描述】
虫洞是很奇特的,因为它是一个**单向**通道,可让你进入虫洞的前达到目的地!他的N(1≤N≤500)个农场被编号为1..N,之间有M(1≤M≤2500)条路径,W(1≤W≤200)个虫洞。FJ作为一个狂热的时间旅行的爱好者,他要做到以下几点:开始在一个区域,通过一些路径和虫洞旅行,他要回到最开时出发的那个区域出发前的时间。也许他就能遇到自己了:)。为了帮助FJ找出这是否是可以或不可以,他会为你提供F个农场的完整的图(1≤F≤5)。所有的路径所花时间都不大于10000秒,所有的虫洞都回到不大于10000秒之前。
【Input】
第1行:一个整数F表示接下来会有F个农场说明。 每个农场第一行:分别是三个空格隔开的整数:N,M和W 第2行到M+1行:三个空格分开的数字(S,E,T)描述,分别为:需要T秒走过S和E之间的双向路径。两个区域可能由一个以上的路径来连接。 第M +2到M+ W+1行:三个空格分开的数字(S,E,T)描述虫洞,描述单向路径,S到E且回溯T秒。
【Output】
F行,每行代表一个农场 每个农场单独的一行,” YES”表示能满足要求,”NO”表示不能满足要求
【样例输入】
2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4
3 1 8【样例输出】
NO
YES题意是问是否能通过虫洞回到过去;虫洞是一条单向路,不但会把你传送到目的地,而且时间会倒退T秒。我们把虫洞看成是一条负权路,问题就转化成求一个图中是否存在负权回路;
Bellman_ford 算法解题
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;const int maxn = 9999999;typedef struct Edge
{int u,v;int weight;
}Edge;
Edge edge[5200];
int d[1010];
int N,M,W,F,all_e;bool bellman_ford()
{int i,j;bool flag;for(i=1;i<=N-1;i++){flag = false;for(j=0;j<all_e;j++){if(d[edge[j].v]>d[edge[j].u]+edge[j].weight){d[edge[j].v]=d[edge[j].u]+edge[j].weight;flag = true;}}if(!flag) return false;//不存在负环}for(i=0;i<all_e;i++){if(d[edge[i].v]>d[edge[i].u]+edge[i].weight)return true;//存在}return false;
}int main()
{int i,j;cin >> F;while(F--){cin >> N >> M >> W;memset(d,maxn,sizeof(d));all_e = 0;int u,v,w;//注意是无向图,双向的for(i=1;i<=M;i++){cin >> u >> v >> w;edge[all_e].u = u;edge[all_e].v = v;edge[all_e++].weight = w;edge[all_e].u = v;edge[all_e].v = u;edge[all_e++].weight = w;}//题目中明确指出,虫洞是单向的for(i=1;i<=W;i++){cin >> u >> v >> w;edge[all_e].u = u;edge[all_e].v = v;edge[all_e++].weight = -w;}if(bellman_ford())cout << "YES\n";elsecout << "NO\n";}return 0;
}Floyd算法
也可以求解,但是,很容易就超时,AC的话时间也会比Bellman_ford算法多很多
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;const int maxn = 99999999;
int map[520][520];
int F,N,M,W;bool bellman_ford()
{int i,j,k;for(k=1;k<=N;k++){for(i=1;i<=N;i++){for(j=1;j<=N;j++){if(map[i][j]>map[i][k]+map[k][j]){map[i][j]=map[i][k]+map[k][j];}}if(map[i][i]<0){return true;}}}return false;
}int main()
{int i,j;cin >> F;while(F--){cin >> N >> M >> W;for(i=0;i<=N;i++){for(j=0;j<=N;j++){if(i==j) map[i][j] = 0;else map[i][j] = maxn;}}int a,b,w;//需要注意的是:正权的边是单向的,负权的边是双向的。for(i=1;i<=M;i++){cin >> a >> b >> w;if(map[a][b]>w){map[a][b] = w;map[b][a] = w;}}for(i=1;i<=W;i++){cin >> a >> b >> w;map[a][b] = -w;}if(bellman_ford())cout << "YES\n";elsecout << "NO\n";}return 0;
}SPFA(Bellman_ford + 队列 优化)
#include <iostream>
#include <queue>
#include <cstring>
#include <cstdio>
#include <stack>
using namespace std;const int maxn = 9999999;
int map[520][520];
int d[520];
bool vis[520];
int enqueue_num[520];
int M,N,W;
int F;bool SPFA()
{memset(vis,false,sizeof(vis));memset(enqueue_num,0,sizeof(enqueue_num));memset(d,maxn,sizeof(d));queue<int> Q;Q.push(1);d[1] = 0;vis[1] = true;enqueue_num[1]++;int v;while(Q.empty()!=1){int u = Q.front();Q.pop();vis[u] = false;for(v=1;v<=N;v++){if(map[u][v]!=maxn){if(d[u]+map[u][v]<d[v]){d[v]=d[u]+map[u][v];if(!vis[v]){Q.push(v);enqueue_num[v]++;if(enqueue_num[v]>=N){return false;//有负圈}vis[v] = true;}}}}}return true;//没有负圈
}int main ()
{int i,j;cin >> F;while(F--){cin >> N >> M >> W;for(i=0;i<=N;i++){for(j=0;j<=N;j++){if(i==j) map[i][j] = 0;else map[i][j] = maxn;}}int a,b,c;for(i=1;i<=M;i++){cin >> a >> b >> c;if(map[a][b]>c){map[a][b] = c;map[b][a] = c;}}for(i=1;i<=W;i++){cin >> a >> b >> c;map[a][b] = -c;}if(SPFA())cout << "NO\n";elsecout << "YES\n";}return 0;
}推荐博客:
最短路径算法—Bellman-Ford(贝尔曼-福特)算法分析与实现(C/C++)
相关文章:
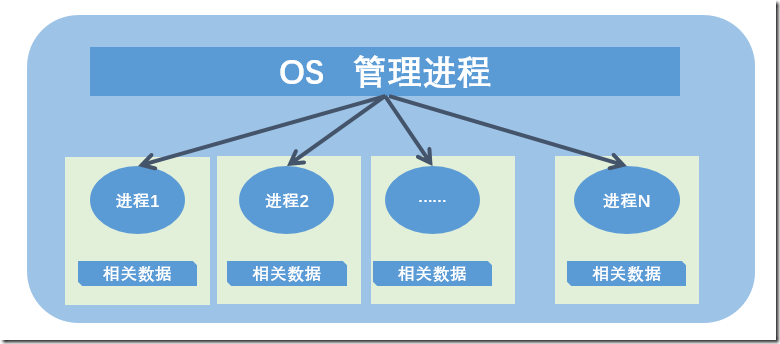
进程控制概念简介 多线程上篇(三)
进程控制 进程的基本数据信息是操作系统控制管理进程的数据集合,这些信息就是用来控制进程的,此处我们说的进程控制就是进程的管理。比如进程有状态,那么进程的创建、终止,状态的切换,这都不是进程自主进行的ÿ…

Android OpenGL使用GLSurfaceView预览视频
Android OpenGL使用GLSurfaceView预览视频第一章 相关知识介绍在介绍具体的功能之前,先对一些主要的类和方法进行一些介绍,这样可以更好的理解整个程序1.1 GLSurfaceView在谷歌的官方文档中是这样解释GLSurfaceView的:An implementation of S…

【Android 基础】Animation 动画介绍和实现
转载自:http://www.cnblogs.com/yc-755909659/p/4290114.html1.Animation 动画类型Android的animation由四种类型组成:XML中alph渐变透明度动画效果scale渐变尺寸伸缩动画效果translate画面转换位置移动动画效果rotate画面转移旋转动画效果JavaCode中Alp…

【Codeforces】1111B - Average Superhero Gang Power
http://codeforces.com/problemset/problem/1111/B n 表示要输入的数据的个数 k 最每一个数据最多可以进行多少次操作 m 一共可以进行多少次操作 一次操作:删除这个数,或者给这个数加1 如果n为1的话,那么只要找出m和k的最小值加到那个数…

刷前端面经笔记(七)
1.描述一下渐进增强和优雅降级 优雅降级(graceful degradation):一开始就构建站点的完整功能,然后针对浏览器测试和修复。渐进增强(progressive enhancement):一开始只构建站点的最少特性,然后不断针对各浏览器追加功能。 2.为什么…

AR资料与连接梳理
AR引擎相关技术 ------------------------------ ARcore:https://developers.google.cn/ar/discover/ ARkit:https://developer.apple.com/arkit/ 以上重点关注,比较新有一些新的功能大家可以自行体验。 ARToolkithttp://www.artoolkit.orght…

Queues 队列
1. Definiation What is a queue? A queue is a list. With a queue, inseration is done at one end (known as rear) whereas deletion is performed at the other end (known as front). 2. Operations 指针对列 无法自定义队长 // array queue #include<iostream> u…

【HDU】1005 Number Sequence (有点可爱)
http://acm.hdu.edu.cn/showproblem.php?pid1005 A number sequence is defined as follows: f(1) 1, f(2) 1, f(n) (A * f(n - 1) B * f(n - 2)) mod 7. Given A, B, and n, you are to calculate the value of f(n). 直接递归求解f(n)的话,会MLE 在计算…

CNCF案例研究:奇虎360
公司:奇虎360地点:中国北京行业:计算机软件 挑战 中国软件巨头奇虎360科技的搜索部门,so.com是中国第二大搜索引擎,市场份额超过35%。该公司一直在使用传统的手动操作来部署环境,随着项目数量的…

C#代码实现对Windows凭据的管理
今天有个任务,那就是使用C#代码实现对windows凭据管理的操作。例如:向windows凭据管理中添加凭据、删除凭据以及查询凭据等功能。于是乎,就开始在网上查找。经过漫长的查询路,终于在一片英文博客中找到了相关代码。经过实验&#…

Android:JNI 与 NDK到底是什么
前言 在Android开发中,使用 NDK开发的需求正逐渐增大但很多人却搞不懂 JNI 与 NDK 到底是怎么回事今天,我将先介绍JNI 与 NDK & 之间的区别,手把手进行 NDK的使用教学,希望你们会喜欢 目录 1. JNI介绍 1.1 简介 定义&…
【ACM】LightOJ - 1008 Fibsieve`s Fantabulous Birthday (找规律,找...)
https://vjudge.net/problem/LightOJ-1008 题目很好理解,第一行表示测试样例的个数,接下来输入一个大于等于1的数,按照格式输出这个数的坐标 蓝色的是 奇数的平方; 红色的是 偶数的平方; 黄色的是对角线:…

Computed property XXX was assigned to but it has no setter
报错视图: 原因: 组件中v-model“XXX”,而XXX是vuex state中的某个变量vuex中是单项流,v-model是vue中的双向绑定,但是在computed中只通过get获取参数值,没有set无法改变参数值解决方法: 1.在co…

OpenGL 矩阵变换
origin refer :http://www.songho.ca/opengl/gl_transform.html#modelviewOpenGL 矩阵变换Related Topics: OpenGL Pipeline, OpenGL Projection Matrix, OpenGL Matrix Class Download: matrixModelView.zip, matrixProjection.zipOverviewOpenGL Transform MatrixExample: GL…

2016.8.11 DataTable合并及排除重复方法
合并: DataTable prosxxx; DataTable pstaryyy; //将两张DataTable合成一张 foreach (DataRow dr in pstar.Rows) { pros.ImportRow(dr); } DataTable设置主键,并判断重复 DataTable allpros xxx; 单列设为主键: //设置第某列为主键 allpros.…
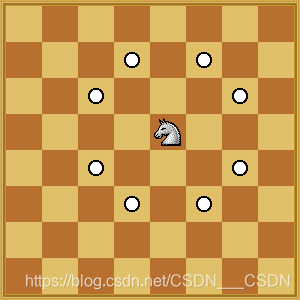
【ACM】LightOJ - 1010 Knights in Chessboard(不是搜索...)
https://vjudge.net/problem/LightOJ-1010 给定一个mn的棋盘,你想把棋子放在哪里。你必须找到棋盘上最多可以放置的骑士数量,这样就不会有两个骑士互相攻击。不熟悉棋手的注意,棋手可以在棋盘上攻击8个位置,如下图所示。 不论输入…

webpack-dev-server 和webapck --watch的区别
webpack-dev-server 和webapck --watch 都可以监测到代码变化 , 区别是:webpack-der-server 监测到代码变化后,浏览器可以看到及时更新的效果,但是并没有自动打包修改的代码; webpack --watch 在监测到代码变化后自动打…
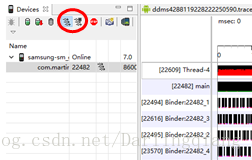
Android 应用进行性能分析/APP/系统性能分析
如何对 Android 应用进行性能分析记录一下自己在使用DDMS的过程:开启AS,打开并运行项目 找到TOOL/选择Android Device Monitor一款 App 流畅与否安装在自己的真机里,玩几天就能有个大概的感性认识。不过通过专业的分析工具可以使我们更好的分…

公钥与私钥,HTTPS详解
1.公钥与私钥原理1)鲍勃有两把钥匙,一把是公钥,另一把是私钥2)鲍勃把公钥送给他的朋友们----帕蒂、道格、苏珊----每人一把。3)苏珊要给鲍勃写一封保密的信。她写完后用鲍勃的公钥加密,就可以达到保密的效果。4)鲍勃收信后,用私钥…

【ACM】杭电OJ 4704 Sum (隔板原理+组合数求和公式+费马小定理+快速幂)
http://acm.hdu.edu.cn/showproblem.php?pid4704 1.隔板原理 1~N有N个元素,每个元素代表一个1.分成K个数,即在(N-1)个空挡里放置(K-1)块隔板 即求组合数C(N-1,0)C(N-1,1)...C(N-1,N-1) 2.组合数求和公式 C(n,0)C(…

Vue 中 CSS 动画原理
下面这段代码,是点击按钮实现hello world显示与隐藏 <div id"root"><div v-if"show">hello world</div><button click"handleClick">按钮</button> </div> let vm new Vue({el: #root,data: {s…

【ACM】UVA - 340 Master-Mind Hints(一定要好好学英语...)
https://vjudge.net/problem/UVA-340 N 表示 密码的个数 第一行是正确的密码 下面的行直到N个0之前,都是猜测的序列,输出的括号(A,B) A表示对应位置与密码相符合的个数,B表示出现在序列中的数字但是位…
SLAM的前世今生
SLAM的前世 从研究生开始切入到视觉SLAM领域,应用背景为AR中的视觉导航与定位。 定位、定向、测速、授时是人们惆怅千年都未能完全解决的问题,最早的时候,古人只能靠夜观天象和司南来做简单的定向。直至元代,出于对定位的需求&a…

No resource found that matches the given name '@style/Theme.AppCompat.Light'
为什么80%的码农都做不了架构师?>>> Android导入项目时出现此问题的解决办法: 1.查看是否存在此目录(D:\android-sdk\extras\android\support\v7\appcompat),若没有此目录,在项目右键Android T…

极限编程 (Extreme Programming) - 迭代计划 (Iterative Planning)
(Source: XP - Iteration Planning) 在每次迭代开始时调用迭代计划会议,以生成该迭代的编程任务计划。每次迭代为1到3周。 客户从发布计划中按照对客户最有价值的顺序选择用户故事进行此次迭代。还选择了要修复的失败验收测试。客户选择的用户故事的估计总计达到上次…
VINS-mono详细解读与实现
VINS-mono详细解读 VINS-mono详细解读 前言 Vins-mono是香港科技大学开源的一个VIO算法,https://github.com/HKUST-Aerial-Robotics/VINS-Mono,是用紧耦合方法实现的,通过单目IMU恢复出尺度,效果非常棒。 感谢他们开源&#x…

mysql+mycat搭建稳定高可用集群,负载均衡,主备复制,读写分离
数据库性能优化普遍采用集群方式,oracle集群软硬件投入昂贵,今天花了一天时间搭建基于mysql的集群环境。 主要思路 简单说,实现mysql主备复制-->利用mycat实现负载均衡。 比较了常用的读写分离方式,推荐mycat,社区活…

【UVA/Codeforces】1584 Circular Sequence / 792B Counting-out Rhyme(就是一个圈儿...)
https://vjudge.net/problem/UVA-1584 1584 Circular Sequence 输入一个字符串,可以以字符串中任意一个字母作为起始,输出字典序最小的那个字符串 两种方法,一种是设两个标记 【样例输入】CGAGTCAGCT 【样例输出】AGCTCGAGTC 一开始 an…

一个free异常引发的异常
有同事反馈说自己的线程不工作,查看堆栈发现其打印如下: #0 0x00007f291f72e7be in __lll_lock_wait_private () from /lib64/libc.so.6 #1 0x00007f291f6c2e4e in _L_lock_9925 () from /lib64/libc.so.6 #2 0x00007f291f6c1101 in free () from /li…
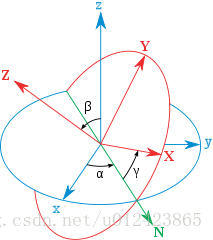
欧拉角和旋转矩阵相互转换
目录 1.参考资料 2.变换矩阵/F/H的svd分解或者旋转矩阵、平移矩阵求解 3. 欧拉角和旋转矩阵可同样表示刚体在三维空间的旋转,下面分享这两者互相转换的方法和核心代码 1.参考资料 2.变换矩阵/F/H的svd分解或者旋转矩阵、平移矩阵求解 欧拉角转旋转矩阵 欧拉角…


