【ACM】杭电OJ 4704 Sum (隔板原理+组合数求和公式+费马小定理+快速幂)
http://acm.hdu.edu.cn/showproblem.php?pid=4704

1.隔板原理
1~N有N个元素,每个元素代表一个1.分成K个数,即在(N-1)个空挡里放置(K-1)块隔板
即求组合数C(N-1,0)+C(N-1,1)+...+C(N-1,N-1)
2.组合数求和公式
C(n,0)+C(n,1)+C(n,2)+.+C(n,n)=2^n
3.费马小定理(降幂)
因为N很大,所以需要费马小定理来降幂
费马小定理是假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。
所以可以把(n-1)对(MOD-1)取余 设余数为K 因为2^(MOD-1)%MOD =1
题目即求2^K %MOD
4.快速幂求解
现在K<=MOD,快速幂的复杂度是O(log₂N),直接套模板就行
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long ll;
using namespace std;
const ll mod = 1000000007;ll quick_mod(ll a,ll b)
{ll ans = 1;while(b){if(b&1){ans = (ans*a)%mod;--b;}a = (a*a)%mod;b >>= 1;}return ans;
}int main ()
{char s[100050];while(scanf("%s",s)!=EOF){if(s[0]=='\0')break;ll i,ans = 0;for(i=0;s[i];i++){ans = (ans*10+s[i]-'0')%(mod-1);}printf("%lld\n",quick_mod(2,ans-1));}return 0;
}同余定理的 简单 应用:LightOJ 1078,HDU 2674,HDU 1212,HDU 2817
相关文章:

Vue 中 CSS 动画原理
下面这段代码,是点击按钮实现hello world显示与隐藏 <div id"root"><div v-if"show">hello world</div><button click"handleClick">按钮</button> </div> let vm new Vue({el: #root,data: {s…

【ACM】UVA - 340 Master-Mind Hints(一定要好好学英语...)
https://vjudge.net/problem/UVA-340 N 表示 密码的个数 第一行是正确的密码 下面的行直到N个0之前,都是猜测的序列,输出的括号(A,B) A表示对应位置与密码相符合的个数,B表示出现在序列中的数字但是位…
SLAM的前世今生
SLAM的前世 从研究生开始切入到视觉SLAM领域,应用背景为AR中的视觉导航与定位。 定位、定向、测速、授时是人们惆怅千年都未能完全解决的问题,最早的时候,古人只能靠夜观天象和司南来做简单的定向。直至元代,出于对定位的需求&a…

No resource found that matches the given name '@style/Theme.AppCompat.Light'
为什么80%的码农都做不了架构师?>>> Android导入项目时出现此问题的解决办法: 1.查看是否存在此目录(D:\android-sdk\extras\android\support\v7\appcompat),若没有此目录,在项目右键Android T…

极限编程 (Extreme Programming) - 迭代计划 (Iterative Planning)
(Source: XP - Iteration Planning) 在每次迭代开始时调用迭代计划会议,以生成该迭代的编程任务计划。每次迭代为1到3周。 客户从发布计划中按照对客户最有价值的顺序选择用户故事进行此次迭代。还选择了要修复的失败验收测试。客户选择的用户故事的估计总计达到上次…
VINS-mono详细解读与实现
VINS-mono详细解读 VINS-mono详细解读 前言 Vins-mono是香港科技大学开源的一个VIO算法,https://github.com/HKUST-Aerial-Robotics/VINS-Mono,是用紧耦合方法实现的,通过单目IMU恢复出尺度,效果非常棒。 感谢他们开源&#x…

mysql+mycat搭建稳定高可用集群,负载均衡,主备复制,读写分离
数据库性能优化普遍采用集群方式,oracle集群软硬件投入昂贵,今天花了一天时间搭建基于mysql的集群环境。 主要思路 简单说,实现mysql主备复制-->利用mycat实现负载均衡。 比较了常用的读写分离方式,推荐mycat,社区活…

【UVA/Codeforces】1584 Circular Sequence / 792B Counting-out Rhyme(就是一个圈儿...)
https://vjudge.net/problem/UVA-1584 1584 Circular Sequence 输入一个字符串,可以以字符串中任意一个字母作为起始,输出字典序最小的那个字符串 两种方法,一种是设两个标记 【样例输入】CGAGTCAGCT 【样例输出】AGCTCGAGTC 一开始 an…

一个free异常引发的异常
有同事反馈说自己的线程不工作,查看堆栈发现其打印如下: #0 0x00007f291f72e7be in __lll_lock_wait_private () from /lib64/libc.so.6 #1 0x00007f291f6c2e4e in _L_lock_9925 () from /lib64/libc.so.6 #2 0x00007f291f6c1101 in free () from /li…
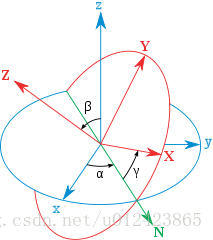
欧拉角和旋转矩阵相互转换
目录 1.参考资料 2.变换矩阵/F/H的svd分解或者旋转矩阵、平移矩阵求解 3. 欧拉角和旋转矩阵可同样表示刚体在三维空间的旋转,下面分享这两者互相转换的方法和核心代码 1.参考资料 2.变换矩阵/F/H的svd分解或者旋转矩阵、平移矩阵求解 欧拉角转旋转矩阵 欧拉角…

【Codeforces】 2A - Winner (map)
http://codeforces.com/problemset/problem/2/A So, if two or more players have the maximum number of points (say, it equals to m) at the end of the game, than wins the one of them who scored at least m points first. 所以只有一个只有一个map不行,…

[译]Godot系列教程一 - 场景与节点
场景(Scene)与节点(Node) 简介 先设想有那么一瞬间你自己不再是一名游戏开发者了,而是一名大厨! 你的装备换成了一套大厨的制服。不要考虑制作游戏的事情,你现在的职责是为你的顾客创建新的可口的食谱。 那么,大厨是怎样创建食谱的…

EOS与以太坊有哪些区别?
想知道更多关于区块链技术知识,请百度【链客区块链技术问答社区】 链客,有问必答!!EOS与以太坊有哪些区别? 以太坊是一个专门为开发和运行去中心化应用(DAPP)搭建的智能合约平台;EOS…

图像特征点检测与匹配评价准则——量化
欢迎转载,转载请注明出处,谢谢! 目前图像匹配中,局部特征匹配占据了绝大部分,常用的局部特征匹配方法有Harris、SIFT、SURF、ORB等等,不同的特征点检测和匹配方法尤其独特的优势和不足; 特征点匹…
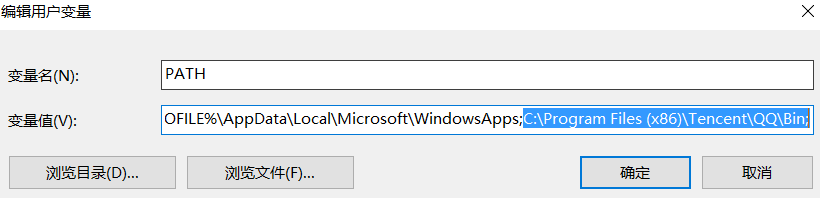
path,classpath
1.path作用. 在环境变量里面配置 winr 打开cmd qq窗口就弹开了。 2.classpath是java里的选项。 java执行java类的时候,会去看这个java类是否在classpath路径下。不在就不能编译转载于:https://www.cnblogs.com/shapeOfMyHeart/p/5975686.html

【Codeforces】401C Team (01010110...)
http://codeforces.com/contest/401/problem/C 题目中,n表示0的个数,m表示1的个数,要求两个0不能连续,三个1不能连续 还要判断能否输出满足要求的序列,不满足输出-1 满足条件以后徐瑶分情况讨论 当1比0多ÿ…

表白这件事,比解 bug 要难多少?
情人节快乐!我是可爱无敌的阿里妹。 今天是个粉红色日子,我们来聊聊和技术无关的“技术活”,比如: “如何表白?” 当技术人碰上动心的姑娘,他的浪漫开关就打开了。 在代码王国里劈荆斩刺的王子,…

特征点匹配+特征检测方法汇总
特征点匹配特征检测方法汇总特征提取与匹配---SURF;SIFT;ORB;FAST;Harris角点匹配方法匹配函数1. OpenCV提供了两种Matching方式:• Brute-force matcher (cv::BFMatcher) //暴力方法找到点集1中每个descriptor在点…
元数据驱动的微服务架构(上)
本次分享有两个部分: 微服务架构需要元数据 介绍微服务与元数据的关系。 一、微服务架构需要元数据 企业IT架构已经发展了多个阶段,一方面是服务化架构的发展,在SOA阶段主要解决应用间集成问题,但随着企业业务的发展,…

【Codeforces】427B Prison Transfer(别让罪犯跑了...)
http://codeforces.com/problemset/problem/427/B 从一串数字中选出连续的长度为c的子串,且子串中的每一个数都不能大于t,问这样的子串有多少个 TLE,看看n的范围就知道了,哎呀呀,有点chun #include <iostream>…

PHPUnit实践三(构建模块化的测试单元)
本系列教程所有的PHPUnit测试基于PHPUnit6.5.9版本,Lumen 5.5框架 目录结构 模块下的目录是符合Lumen的模块结构的如:Controllers、Models、Logics等是Lumen模块目录下的结构目录如果有自己的目录同级分配即可,如我这里的Requests 整体结构 ├…
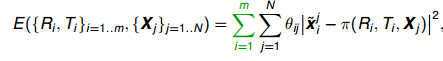
SLAM笔记(五)光束平差法(Bundle Adjustment)
1.什么是光束平差法 前边的八点法,五点法等可以求出闭式解的前提是已经知道确切的点对。但实际情况中往往存在大量的噪声,点与点不是精确地对应甚至出现一些错误匹配。 光束平差法由Bundle Adjustment翻译得来,有两层意思: 对场…

【Code forces】63B Settlers' Training
http://codeforces.com/problemset/problem/63/B 给你一串数字,直到所有数字都变为k为止,相同的数为一组,在一次中,所有不同的数都加1 1 2 2 3 → 2 2 3 4 → 2 3 4 4 → 3 4 4 4 → 4 4 4 4 #include <ios…

[elixir! #0007] [译] 理解Elixir中的宏——part.5 重塑AST by Saša Jurić
上一章我们提出了一个基本版的deftraceable宏,能让我们编写可跟踪的函数。宏的最终版本有一些剩余的问题,今天我们将解决其中的一个——参数模式匹配。 今天的练习表明我们必须仔细考虑宏可能接收到的输入。 问题 正如我上一次暗示的那样,当前…

vue-cli3环境变量与分环境打包
第一步 : 了解环境变量概念 我们可以根目录中的下列文件来指定环境变量: .env # 在所有的环境中被载入 .env.local # 在所有的环境中被载入,但会被 git 忽略 .env.[mode] # 只在指定的模式中被载入 .env.[mode].local # 只在指定…
SLAM闭合回环————视觉词典BOW小结
在目前实际的视觉SLAM中,闭环检测多采用DBOW2模型https://github.com/dorian3d/DBoW2,而bag of words 又运用了数据挖掘的K-means聚类算法,笔者只通过bag of words 模型用在图像处理中进行形象讲解,并没有涉及太多对SLAM的闭环检测…

【Codeforces】53D Physical Education (有点像冒泡)
http://codeforces.com/problemset/problem/53/D 从上面所给的序列变成下面所给的序列 交换的时候只能交换相邻的两个数字 输出每一步的交换方法,输出的是该元素在序列中的位置(第一个数的位置是1) 不要求输出步数最少的那一种方法 当同…

js脚本冷知识
js中有个很恶心的写法。比如这个var adsf(function(){})();这样的写法,主要是原生的,能在dom元素加载完之后实现自动加载这个脚本文件到里面去。可以验证这个(function(){.......)();在.......里面可以直接…

Python中is同一性运算符和==相等运算符区别
2019独角兽企业重金招聘Python工程师标准>>> 在区分is和这两种运算符区别之前,需要知道Python中对象包含的三个基本要素,分别是:id(身份标识)、type(数据类型)和value(值)。 比较对象的value(值) 是python标准操作符中的比较操作符…
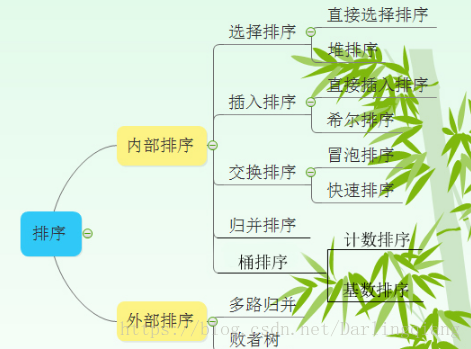
C++实现十大排序算法(冒泡,选择,插入,归并,快速,堆,希尔,桶,计数,基数)排序算法时间复杂度、空间复杂度、稳定性比较(面试经验总结)
排序算法分类 内部排序算法又分为基于比较的排序算法和不基于比较的排序算法,其分类如下: 比较排序: 直接插入排序 希尔排序 (插入) 冒泡排序 快速排序 (交换) 直接选择排序 堆排序(选择&#…
