C++实现十大排序算法(冒泡,选择,插入,归并,快速,堆,希尔,桶,计数,基数)排序算法时间复杂度、空间复杂度、稳定性比较(面试经验总结)
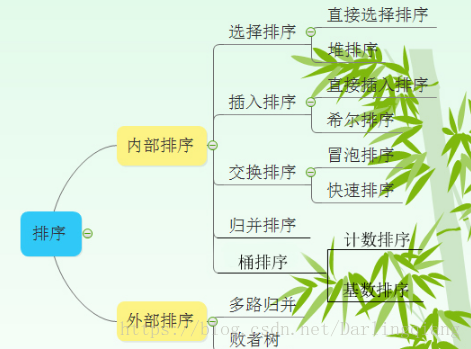
排序算法分类
内部排序算法又分为基于比较的排序算法和不基于比较的排序算法,其分类如下:
比较排序: 直接插入排序 希尔排序 (插入) 冒泡排序 快速排序 (交换) 直接选择排序 堆排序(选择) 归并排序
非比较排序:桶排序 基数排序
排序算法比较表格
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(1) | 是 |
| 选择排序 | O(n2) | O(n2) | O(1) | 不是 |
| 直接插入排序 | O(n2) | O(n2) | O(1) | 是 |
| 归并排序 | O(nlogn) | O(nlogn) | O(n) | 是 |
| 快速排序 | O(nlogn) | O(n2) | O(logn) | 不是 |
| 堆排序 | O(nlogn) | O(nlogn) | O(1) | 不是 |
| 希尔排序 | O(nlogn) | O(ns) | O(1) | 不是 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | 是 |
| 基数排序 | O(N∗M) | O(N∗M) | O(M) | 是 |
注:
1 归并排序可以通过手摇算法将空间复杂度降到O(1),但是时间复杂度会提高。
2 基数排序时间复杂度为O(N*M),其中N为数据个数,M为数据位数。
辅助记忆
- 时间复杂度记忆-
- 冒泡、选择、直接 排序需要两个for循环,每次只关注一个元素,平均时间复杂度为O(n2)O(n2)(一遍找元素O(n),一遍找位置O(n))
- 快速、归并、希尔、堆基于二分思想,log以2为底,平均时间复杂度为O(nlogn))(一遍找元素O(n),一遍找位置O(logn))
- 稳定性记忆-“快希选堆”(快牺牲稳定性)
- 排序算法的稳定性:排序前后相同元素的相对位置不变,则称排序算法是稳定的;否则排序算法是不稳定的。
原理理解
1 冒泡排序
1.1 过程
冒泡排序从小到大排序:一开始交换的区间为0~N-1,将第1个数和第2个数进行比较,前面大于后面,交换两个数,否则不交换。再比较第2个数和第三个数,前面大于后面,交换两个数否则不交换。依次进行,最大的数会放在数组最后的位置。然后将范围变为0~N-2,数组第二大的数会放在数组倒数第二的位置。依次进行整个交换过程,最后范围只剩一个数时数组即为有序。(相邻两项比较,将最大数选出,放到最后位置)站在位置的角度考虑
2 动图
1.3 核心代码(函数)
//array[]为待排序数组,n为数组长度
void BubbleSort(int array[], int n)
{int i, j, k;for(i=0; i<n-1; i++)for(j=0; j<n-1-i; j++){if(array[j]>array[j+1]){k=array[j];array[j]=array[j+1];array[j+1]=k;}}
}2 选择排序
2.1 过程
选择排序从小到大排序:一开始从0~n-1区间上选择一个最小值,将其放在位置0上,然后在1~n-1范围上选取最小值放在位置1上。重复过程直到剩下最后一个元素,数组即为有序。
2.2 动图
2.3 核心代码(函数)
//array[]为待排序数组,n为数组长度
void selectSort(int array[], int n)
{int i, j ,min ,k;for( i=0; i<n-1; i++){min=i; //每趟排序最小值先等于第一个数,遍历剩下的数for( j=i+1; j<n; j++) //从i下一个数开始检查{if(array[min]>array[j]){min=j;}}if(min!=i){k=array[min];array[min]=array[i];array[i]=k;}}
}3.1 过程
插入排序从小到大排序:首先位置1上的数和位置0上的数进行比较,如果位置1上的数大于位置0上的数,将位置0上的数向后移一位,将1插入到0位置,否则不处理。位置k上的数和之前的数依次进行比较,如果位置K上的数更大,将之前的数向后移位,最后将位置k上的数插入不满足条件点,反之不处理。
3.2 动图
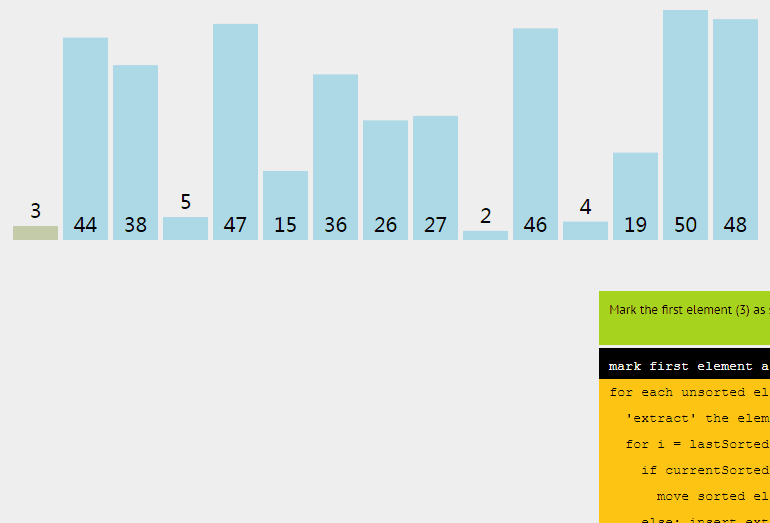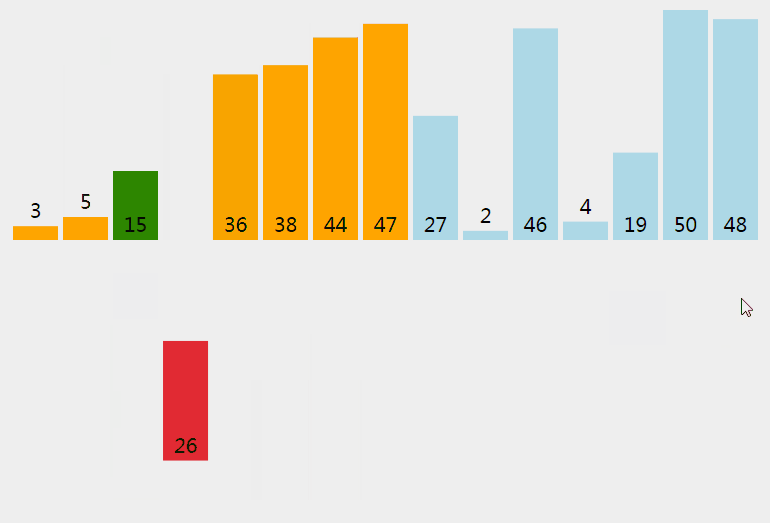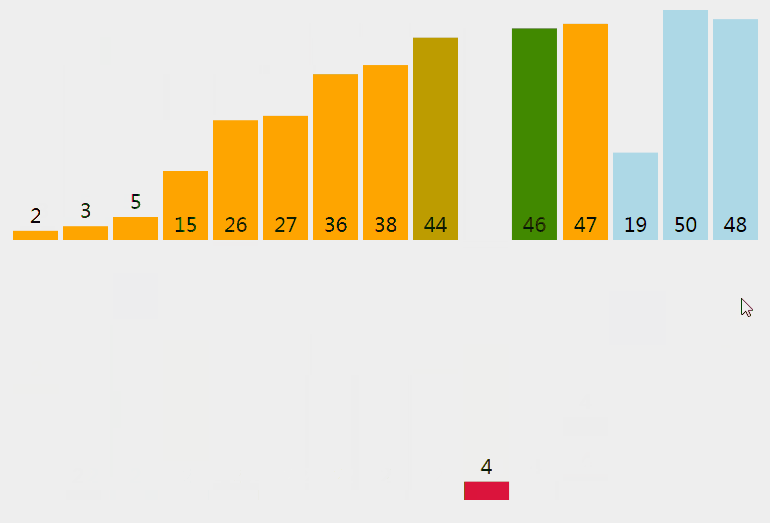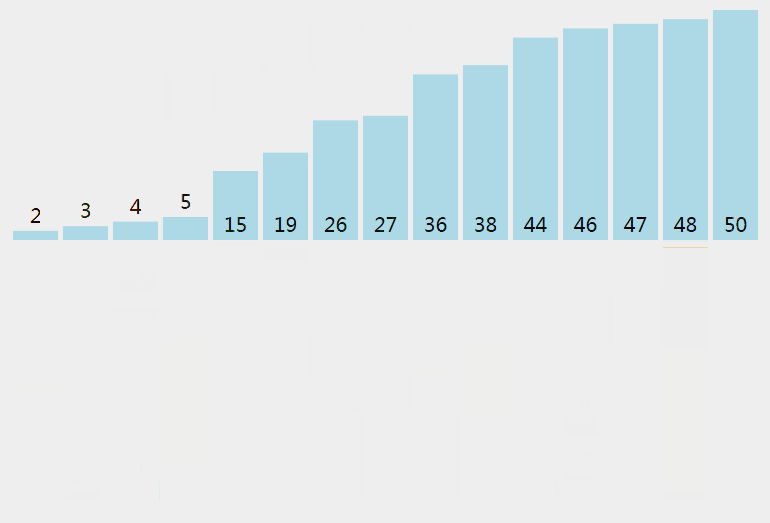
3.3 核心代码(函数)
//array[]为待排序数组,n为数组长度
void insertSort(int array[], int n)
{int i,j,temp;for( i=1;i<n;i++){if(array[i]<array[i-1]){temp=array[i];for( j=i;array[j-1]>temp;j--){array[j]=array[j-1];}array[j]=temp;}}
}4 归并排序
4.1 过程
归并排序从小到大排序:首先让数组中的每一个数单独成为长度为1的区间,然后两两一组有序合并,得到长度为2的有序区间,依次进行,直到合成整个区间。
4.2 动图
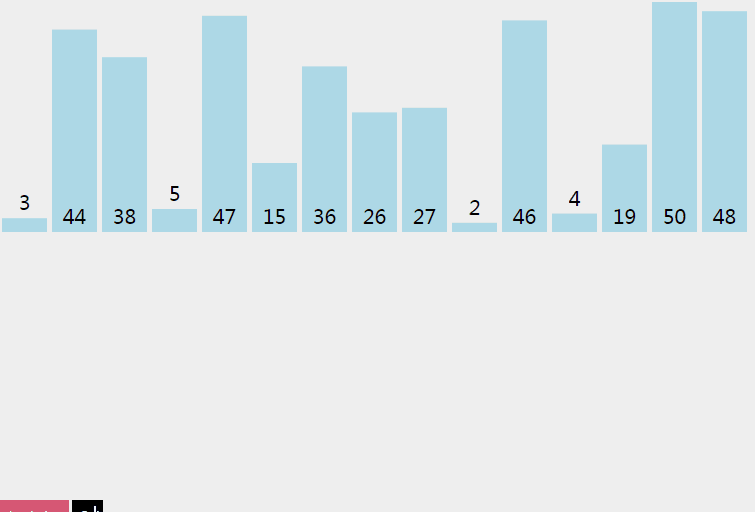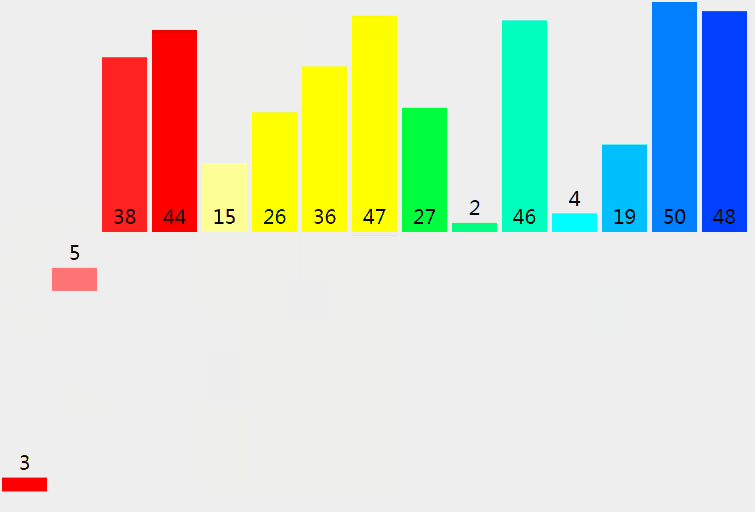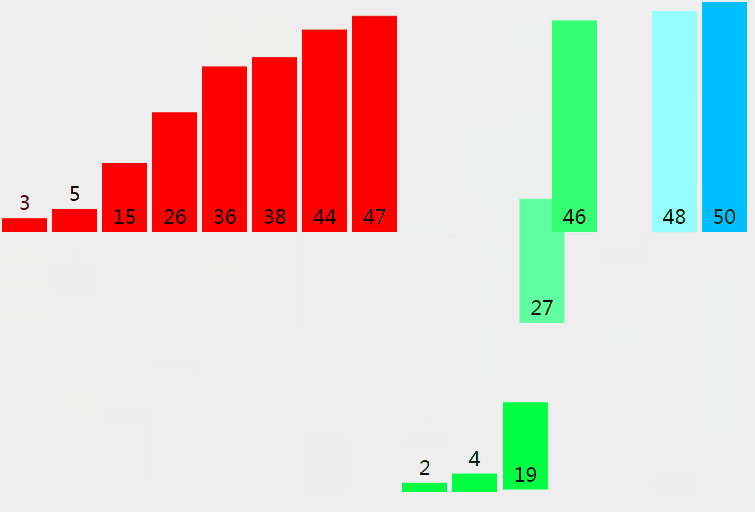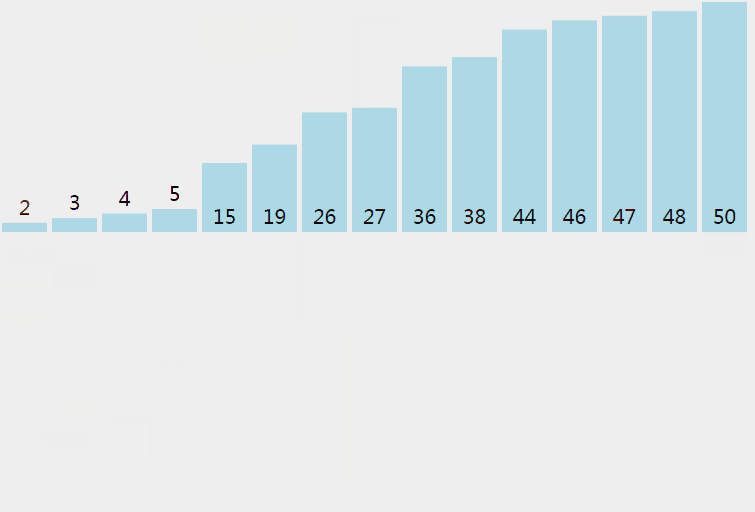
4.3 核心代码(函数)
- 递归实现
实现归并,并把数据都放在list1里面
void merging(int *list1, int list1_size, int *list2, int list2_size)
{int i=0, j=0, k=0, m=0;int temp[MAXSIZE];while(i < list1_size && j < list2_size){if(list1[i]<list2[j]){temp[k++] = list1[i++];}else{temp[k++] = list2[j++];}}while(i<list1_size){temp[k++] = list1[i++];}while(j<list2_size){temp[k++] = list2[j++];}for(m=0; m < (list1_size+list2_size); m++){list1[m]=temp[m];}
}
//如果有剩下的,那么说明就是它是比前面的数组都大的,直接加入就可以了
void mergeSort(int array[], int n)
{if(n>1){int *list1 = array;int list1_size = n/2;int *list2 = array + n/2;int list2_size = n-list1_size;mergeSort(list1, list1_size);mergeSort(list2, list2_size);merging(list1, list1_size, list2, list2_size);}
}
//归并排序复杂度分析:一趟归并需要将待排序列中的所有记录
//扫描一遍,因此耗费时间为O(n),而由完全二叉树的深度可知,
//整个归并排序需要进行[log2n],因此,总的时间复杂度为
//O(nlogn),而且这是归并排序算法中平均的时间性能
//空间复杂度:由于归并过程中需要与原始记录序列同样数量级的
//存储空间去存放归并结果及递归深度为log2N的栈空间,因此空间
//复杂度为O(n+logN)
//也就是说,归并排序是一种比较占内存,但却效率高且稳定的算法 - 迭代实现
void MergeSort(int k[],int n)
{ int i,next,left_min,left_max,right_min,right_max; //动态申请一个与原来数组一样大小的空间用来存储int *temp = (int *)malloc(n * sizeof(int)); //逐级上升,第一次比较2个,第二次比较4个,第三次比较8个。。。 for(i=1; i<n; i*=2) { //每次都从0开始,数组的头元素开始 for(left_min=0; left_min<n-i; left_min = right_max) { right_min = left_max = left_min + i; right_max = left_max + i; //右边的下标最大值只能为n if(right_max>n) { right_max = n; } //next是用来标志temp数组下标的,由于每次数据都有返回到K, //故每次开始得重新置零 next = 0; //如果左边的数据还没达到分割线且右边的数组没到达分割线,开始循环 while(left_min<left_max&&right_min<right_max) { if(k[left_min] < k[right_min]) { temp[next++] = k[left_min++]; } else { temp[next++] = k[right_min++]; } } //上面循环结束的条件有两个,如果是左边的游标尚未到达,那么需要把 //数组接回去,可能会有疑问,那如果右边的没到达呢,其实模拟一下就可以 //知道,如果右边没到达,那么说明右边的数据比较大,这时也就不用移动位置了 while(left_min < left_max) { //如果left_min小于left_max,说明现在左边的数据比较大 //直接把它们接到数组的min之前就行 k[--right_min] = k[--left_max]; } while(next>0) { //把排好序的那部分数组返回该k k[--right_min] = temp[--next]; } } }
}
//非递归的方法,避免了递归时深度为log2N的栈空间,
//空间只是用到归并临时申请的跟原来数组一样大小的空间,并且在时间性能上也有一定的提升,
//因此,使用归并排序是,尽量考虑用非递归的方法。5 快速排序
5.1 过程
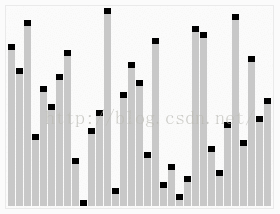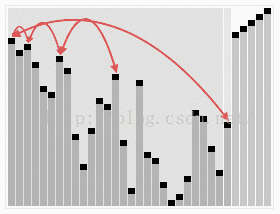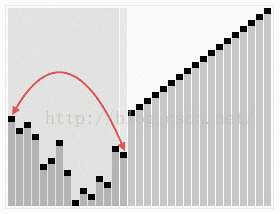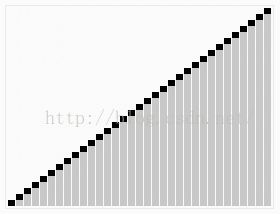
快速排序从小到大排序:在数组中随机选一个数(默认数组首个元素),数组中小于等于此数的放在左边,大于此数的放在右边,再对数组两边递归调用快速排序,重复这个过程。
5.2 动图
5.3 核心代码(函数)
推荐程序(好理解)
//接口调整
void adjust_quicksort(int k[],int n)
{ quicksort(k,0,n-1);
}
void quicksort(int a[], int left, int right)
{ int i,j,t,temp; if(left>right) //(递归过程先写结束条件)return; temp=a[left]; //temp中存的就是基准数 i=left; j=right; while(i!=j) { //顺序很重要,要先从右边开始找(最后交换基准时换过去的数要保证比基准小,因为基准 //选取数组第一个数,在小数堆中) while(a[j]>=temp && i<j) j--; //再找右边的 while(a[i]<=temp && i<j) i++; //交换两个数在数组中的位置 if(i<j) { t=a[i]; a[i]=a[j]; a[j]=t; } } //最终将基准数归位 (之前已经temp=a[left]过了,交换只需要再进行两步)a[left]=a[i]; a[i]=temp; quicksort(left,i-1);//继续处理左边的,这里是一个递归的过程 quicksort(i+1,right);//继续处理右边的 ,这里是一个递归的过程
} 6.1 过程
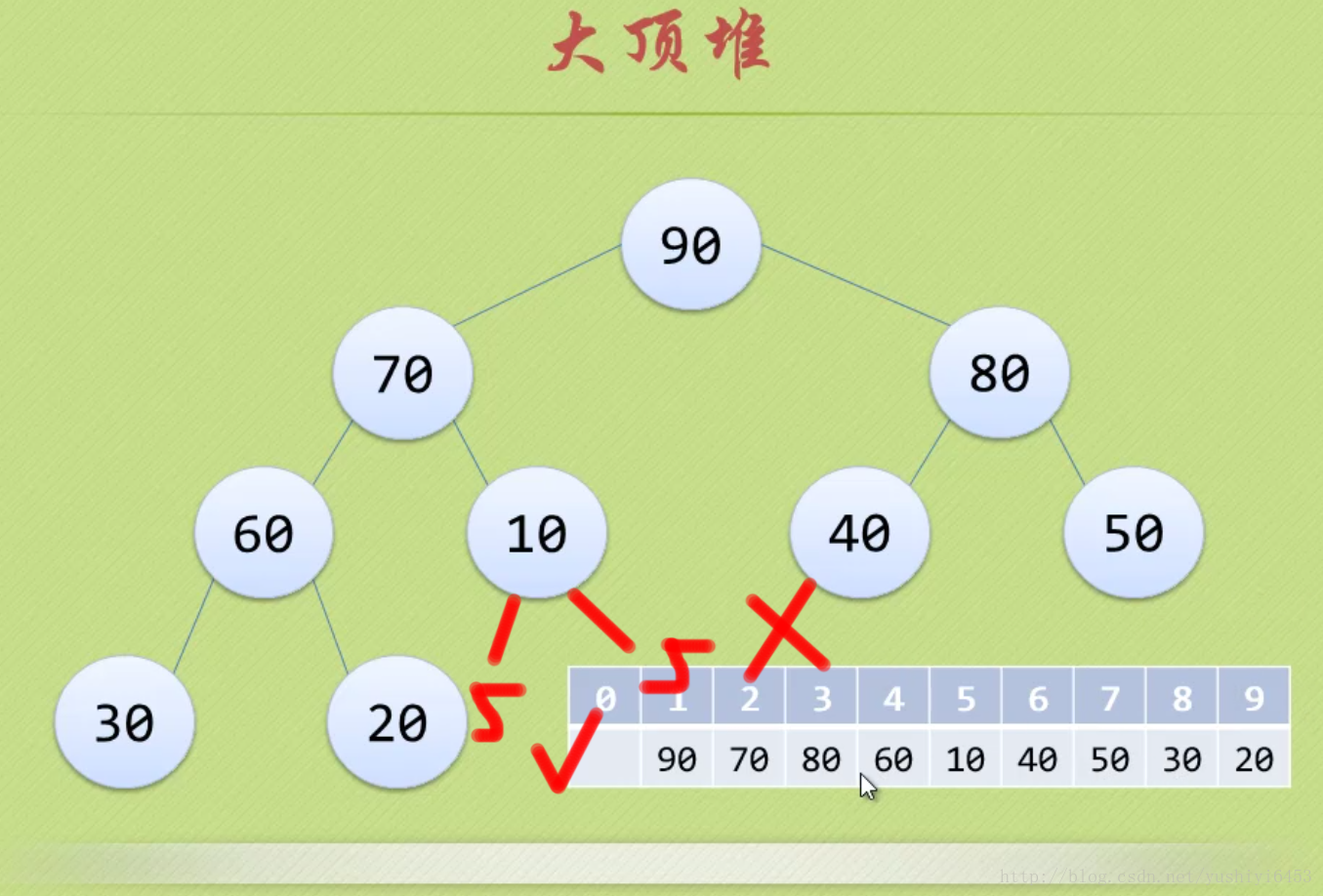
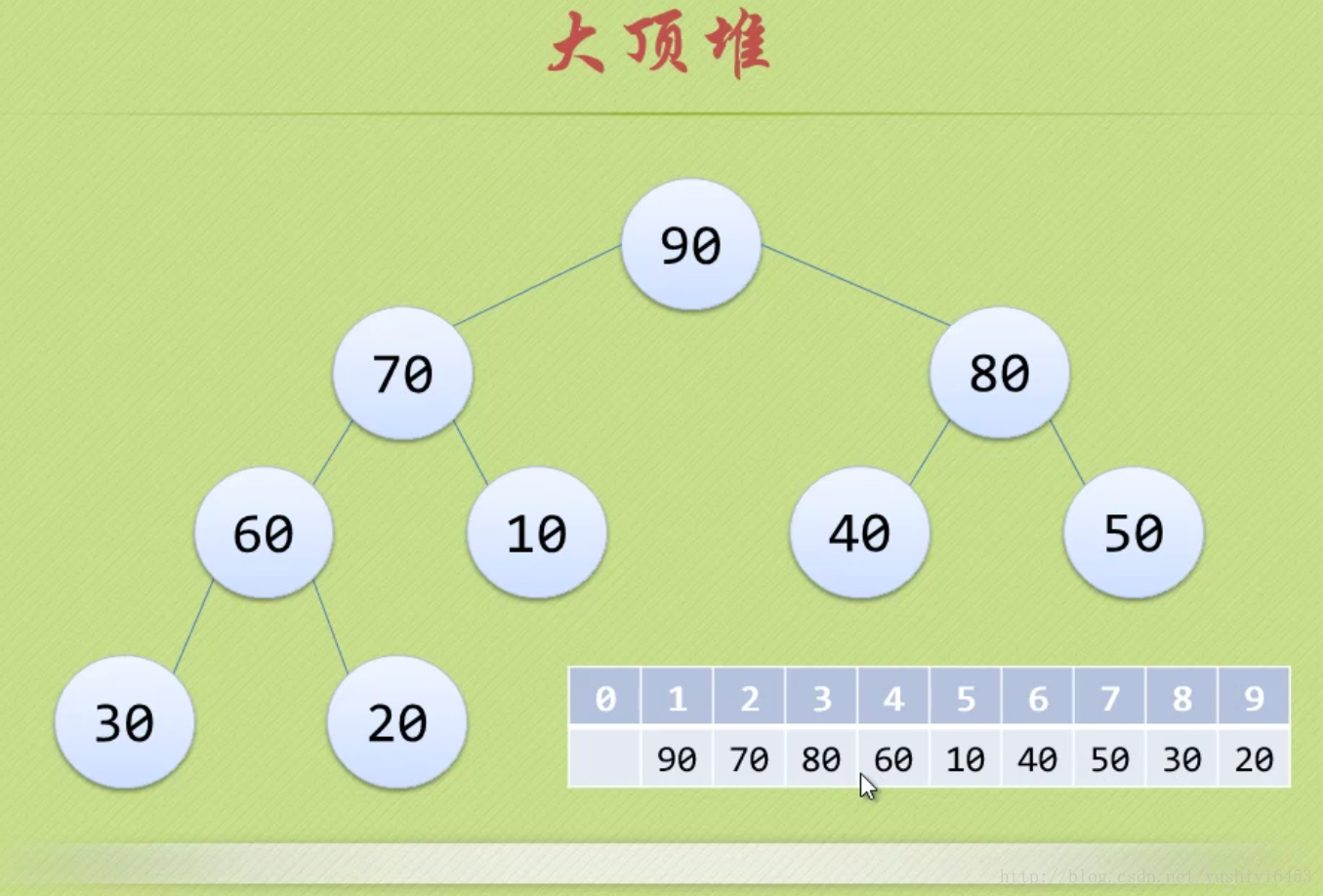
堆排序从小到大排序:首先将数组元素建成大小为n的大顶堆,堆顶(数组第一个元素)是所有元素中的最大值,将堆顶元素和数组最后一个元素进行交换,再将除了最后一个数的n-1个元素建立成大顶堆,再将最大元素和数组倒数第二个元素进行交换,重复直至堆大小减为1。
注:完全二叉树
假设二叉树深度为n,除了第n层外,n-1层节点都有两个孩子,第n层节点连续从左到右。如下图注:大顶堆
大顶堆是具有以下性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值。
即,根节点是堆中最大的值,按照层序遍历给节点从1开始编号,则节点之间满足如下关系:(1<=i<=n/2)
6.2 动图
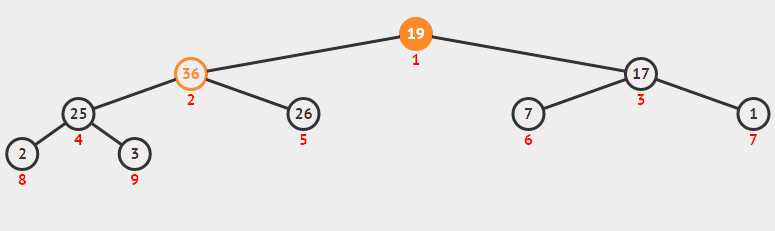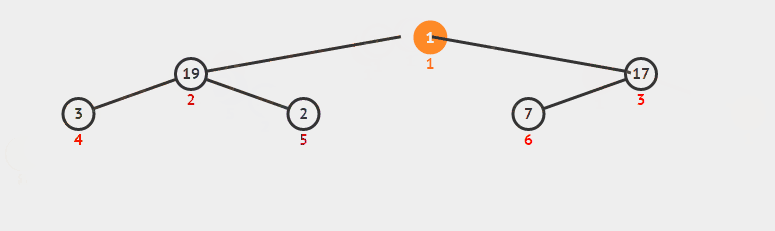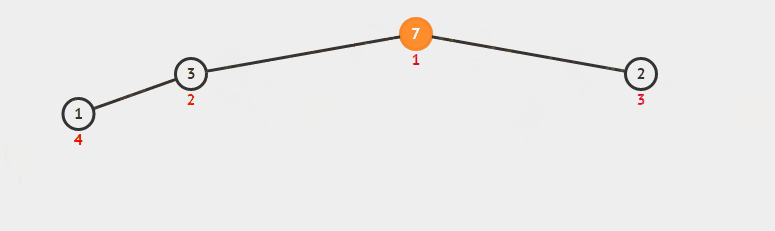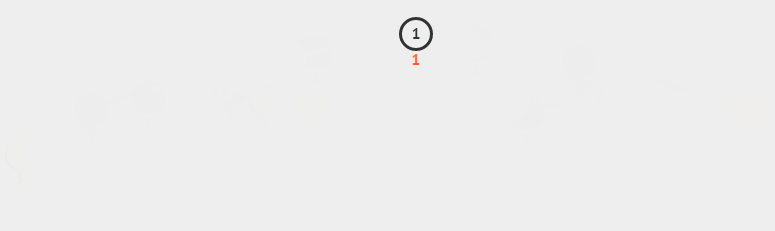

6.3 核心代码(函数)
注意!!!数组从1开始,1~n
void heapSort(int array[], int n)
{int i;for (i=n/2;i>0;i--){HeapAdjust(array,i,n);//从下向上,从右向左调整}for( i=n;i>1;i--){swap(array, 1, i);HeapAdjust(array, 1, i-1);//从上到下,从左向右调整}
}
void HeapAdjust(int array[], int s, int n )
{int i,temp;temp = array[s];for(i=2*s;i<=n;i*=2){if(i<n&&array[i]<array[i+1]){i++;}if(temp>=array[i]){break;}array[s]=array[i];s=i;}array[s]=temp;
}
void swap(int array[], int i, int j)
{int temp;temp=array[i];array[i]=array[j];array[j]=temp;
}7 希尔排序
7.1 过程
希尔排序是插入排序改良的算法,希尔排序步长从大到小调整,第一次循环后面元素逐个和前面元素按间隔步长进行比较并交换,直至步长为1,步长选择是关键。
7.2 动图

7.3 核心程序(函数)
//下面是插入排序
void InsertSort( int array[], int n)
{int i,j,temp;for( i=0;i<n;i++ ){if(array[i]<array[i-1]){temp=array[i];for( j=i-1;array[j]>temp;j--){array[j+1]=array[j];}array[j+1]=temp;}}
}
//在插入排序基础上修改得到希尔排序
void SheelSort( int array[], int n)
{int i,j,temp;int gap=n; //~~~~~~~~~~~~~~~~~~~~~do{gap=gap/3+1; //~~~~~~~~~~~~~~~~~~for( i=gap;i<n;i++ ){if(array[i]<array[i-gap]){temp=array[i];for( j=i-gap;array[j]>temp;j-=gap){array[j+gap]=array[j];}array[j+gap]=temp;}}}while(gap>1); //~~~~~~~~~~~~~~~~~~~~~~}8 桶排序(基数排序和基数排序的思想)
8.1 过程
桶排序是计数排序的变种,把计数排序中相邻的m个”小桶”放到一个”大桶”中,在分完桶后,对每个桶进行排序(一般用快排),然后合并成最后的结果。
8.2 图解
8.3 核心程序
#include <stdio.h>
int main()
{int a[11],i,j,t;for(i=0;i<=10;i++)a[i]=0; //初始化为0for(i=1;i<=5;i++) //循环读入5个数{scanf("%d",&t); //把每一个数读到变量t中a[t]++; //进行计数(核心行)}for(i=0;i<=10;i++) //依次判断a[0]~a[10]for(j=1;j<=a[i];j++) //出现了几次就打印几次printf("%d ",i);getchar();getchar(); //这里的getchar();用来暂停程序,以便查看程序输出的内容//也可以用system("pause");等来代替return 0;
}9 计数排序
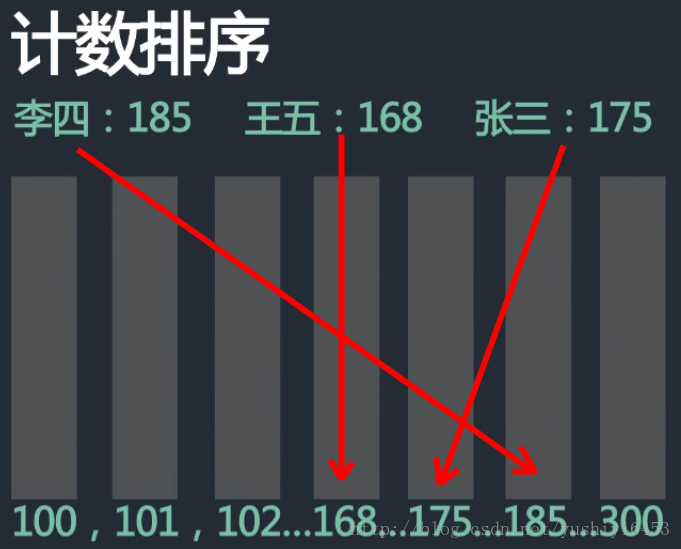
9.1 过程
算法的步骤如下:
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
9.2 图解
9.3 核心程序(函数)
程序1:
#define NUM_RANGE (100) //预定义数据范围上限,即K的值void counting_sort(int *ini_arr, int *sorted_arr, int n) //所需空间为 2*n+k
{ int *count_arr = (int *)malloc(sizeof(int) * NUM_RANGE); int i, j, k; //初始化统计数组元素为值为零 for(k=0; k<NUM_RANGE; k++){ count_arr[k] = 0; } //统计数组中,每个元素出现的次数 for(i=0; i<n; i++){ count_arr[ini_arr[i]]++; } //统计数组计数,每项存前N项和,这实质为排序过程for(k=1; k<NUM_RANGE; k++){ count_arr[k] += count_arr[k-1]; } //将计数排序结果转化为数组元素的真实排序结果for(j=n-1 ; j>=0; j--){ int elem = ini_arr[j]; //取待排序元素int index = count_arr[elem]-1; //待排序元素在有序数组中的序号sorted_arr[index] = elem; //将待排序元素存入结果数组中count_arr[elem]--; //修正排序结果,其实是针对算得元素的修正} free(count_arr);
} 程序2:C++(最大最小压缩桶数)
public static void countSort(int[] arr) {if (arr == null || arr.length < 2) {return;}int min = arr[0];int max = arr[0];for (int i = 1; i < arr.length; i++) {min = Math.min(arr[i], min);max = Math.max(arr[i], max);}int[] countArr = new int[max - min + 1];for (int i = 0; i < arr.length; i++) {countArr[arr[i] - min]++;}int index = 0;for (int i = 0; i < countArr.length; i++) {while (countArr[i]-- > 0) {arr[index++] = i + min;}
}10.1 过程
基数排序是基于数据位数的一种排序算法。
它有两种算法
①LSD–Least Significant Digit first 从低位(个位)向高位排。
②MSD– Most Significant Digit first 从高位向低位(个位)排。
时间复杂度O(N*最大位数)。
空间复杂度O(N)。
10.2 图解

对a[n]按照个位0~9进行桶排序: 
对b[n]进行累加得到c[n],用于b[n]中重复元素计数
!!!b[n]中的元素为temp中的位置!!!跳跃的用++补上: 
temp数组为排序后的数组,写回a[n]。temp为按顺序倒出桶中的数据(联合b[n],c[n],a[n]得到),重复元素按顺序输出:
10.3 核心程序
1.1 VS2010程序
#include "stdafx.h"
#include "stdio.h"
#include <stdlib.h>void BubbleSort(int array[], int n){int i,j,k,count1=0, count2=0;for(i=0; i<n-1; i++)for(j=n-1; j>i; j--){count1++;if(array[j-1]>array[j]){count2++;k=array[j-1];array[j-1]=array[j];array[j]=k;}}printf("总共的循环次序为:%d, 总共的交换次序为:%d\n\n", count1, count2);
}int main(int argc, _TCHAR* argv[])
{int as[]={0,1,2,3,4,6,8,5,9,7};BubbleSort(as, 10);for(int i=0; i<10; i++){printf("%d", as[i]);}printf("\n\n");system("pause");return 0;
}1.2 执行程序(OJ)
#include <stdio.h>void BubbleSort(int array[], int n){int i,j,k,count1=0, count2=0;for(i=0; i<n-1; i++)for(j=n-1; j>i; j--){count1++;if(array[j-1]>array[j]){count2++;k=array[j-1];array[j-1]=array[j];array[j]=k;}}printf("总共的循环次序为:%d, 总共的交换次序为:%d\n\n", count1, count2);
}int main()
{int as[]={0,1,2,3,4,6,8,5,9,7};BubbleSort(as, 10);int i=0;for(i=0; i<10; i++){printf("%d", as[i]);}return 0;
}2 关于交换的优化
不用中间变量进行交换
C语言实现数组动态输入
#include <stdio.h>
#include <assert.h> //断言头文件
#include <stdlib.h> int main(int argc, char const *argv[])
{ int size = 0; scanf("%d", &size); //首先输入数组个数assert(size > 0); //判断数组个数是否非法int *array = (int *)calloc(size, sizeof(int)); //动态分配数组if(!R1) { return; //申请空间失败 } int i = 0; for (i = 0; i < size; ++i) { scanf("%d", &array[i]); } mergeSort(array, size); printArray(array, size); free(array); return 0;
} 注:
1.colloc与malloc类似,但是主要的区别是存储在已分配的内存空间中的值默认为0,使用malloc时,已分配的内存中可以是任意的值.
2.colloc需要两个参数,第一个是需要分配内存的变量的个数,第二个是每个变量的大小.
参考博文
[1]https://blog.csdn.net/yushiyi6453
[2]https://blog.csdn.net/yushiyi6453/article/details/76407640
版权声明:本文为博主原创文章,未经博主允许不得转载。
相关文章:

32位处理器是什么意思
问题描述:朋友那个32位处理器,2的32次方算出来的单位是不是应该是4294967296位(bit)吧,怎么就成字节了呢?单位错了,那个32位是指32位地址总线,而不是32位数据。地址的数量单位是个&a…

【Codeforces】913C Party Lemonade (贪...)。
http://codeforces.com/contest/913/problem/C 这个题和以前见过的有点不一样,可以重复选择,这个有点emmm 首先将a数组优化,举个例子,如果1L20元,2L50元,那么将a[1]赋值为40,而不是50。 之后…

GDB 调试 Mysql 实战(二)GDB 调试打印
背景 在 https://mengkang.net/1328.html 实验中,我们通过optimizer_trace发现group by会使用intermediate_tmp_table,而且里面的的row_length是20,抱着"打破砂锅问到底"的求学精神,所以想通过 gdb 调试源码的方式看这个…

移动端AR的适用分析(二)
移动端AR的适用分析(二)1. 单目SLAM难点 2. 视觉SLAM难点 3. 可能的解决思路 单目slam的障碍来自于理论和实践两个方面。理论障碍可以看做是固有的,无法通过硬件选型或软件算法来解决的,例如单目初始化和尺度问题。实践问题包括计…

新的理念、 新的解决方案、 新的Azure Stack技术预览
Jeffrey Snover 我们很高兴地宣布︰ Azure Stack Technical Preview 2(TP2)已发布!我们朝着向您的数据中心提供Azure服务能力的目标又更近一步。自发布第一个技术预览版(TP1)以来,我们访问了很多用户&…

【HDU】1084 What Is Your Grade? (结构体 sort)
http://acm.hdu.edu.cn/showproblem.php?pid1084 题目的关键: 1、Note, only 1 student will get the score 95 when 3 students have solved 4 problems. If you can solve 4 problems, you can also get a high score 95 or 90 (you can get the former(前者)…

FastDFS之Linux下搭建
1.软件环境 CentOS6.5 FastDFS v5.05 libfastcommon- - master.zip(是从 FastDFS 和 FastDHT 中提取出来的公共 C 函数库) fastdfs- - nginx- - module_v1.16.tar.gz nginx- - 1.6.2.tar.gz fastdfs_client_java._v1.25.tar.gz 2.FastDFS集群规划 描述 …
Linux进程与线程的区别 详细总结(面试经验总结)
首先,简要了解一下进程和线程。对于操作系统而言,进程是核心之核心,整个现代操作系统的根本,就是以进程为单位在执行任务。系统的管理架构也是基于进程层面的。在按下电源键之后,计算机就开始了复杂的启动过程…

【HDU/POJ/ZOJ】Calling Extraterrestrial Intelligence Again (素数打表模板)
http://poj.org/problem?id1411 POJ http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode1689 ZOJ http://acm.hdu.edu.cn/showproblem.php?pid1239 HDU 都是同一个题,但是可能你在HDU上AC,在POJ和ZOJ上是TLE(所以还有待…

[AVR]使用AVR单片机驱动舵机
最近参加了三系举办的小车比赛(好像叫什么"驭远杯")。领导要求我驱动3-4个舵机。研究了几日,总算折腾出一个方案..、 1.舵机驱动的基本原理 (可以参考http://blog.sina.com.cn/s/blog_8240cbef01018hu1.html) "控制信号由接收…

高阶函数的使用
问题 字节跳动面试时问题:原函数例如fetchData是一个异步函数,尝试从服务器端获取一些信息并返回一个Promise。写一个新的函数可以自动重试一定次数,并且在使用上和原函数没有区别。 思路 这个问题其实不是很难,不过可能是太菜了紧…

内存溢出和内存泄漏的定义,产生原因以及解决方法(面试经验总结)
一、定义(概念与区别) 内存溢出 out of memory,是指程序在申请内存时,没有足够的内存空间供其使用,出现out of memory;比如申请 了一个integer,但给它存了long才能存下的数,那就是内存溢出。 …

【Codeforces】716B Complete the Word (26个字母)
http://codeforces.com/contest/716/problem/B 给你一个字符串该字符串中是否存在长度为26且这26个字母没有重复 一个满足上述条件但是部分区域是问号的话,需要用剩下的字母覆盖掉问号,其余部分的问号可以随便赋值 没有的话输出-1 暴力即可。 #incl…

MySQL ERROR 1878 解决办法
MySQL ERROR 1878报错解决办法错误重现Part1:大表修改字段mysql> ALTER TABLE erp-> ADD COLUMN eas_status tinyint(3) unsigned NOT NULL DEFAULT 0 AFTER totalprice;ERROR 1878 (HY000): Temporary file write failure.mysql> \q这里可以看到,添加字…

共享程序集和强命名程序集(3):强命名程序集的一些作用
强命名程序集能防篡改 用私钥对程序集进行签名,并将公钥和签名嵌入程序集,CLR就可以炎症程序集未被修改或破坏。程序集安装到GAC时,系统对包含清单的那个文件的内容进行哈希处理,将Hash值与PE文件中嵌入的RSA数字签名进行比较。如…
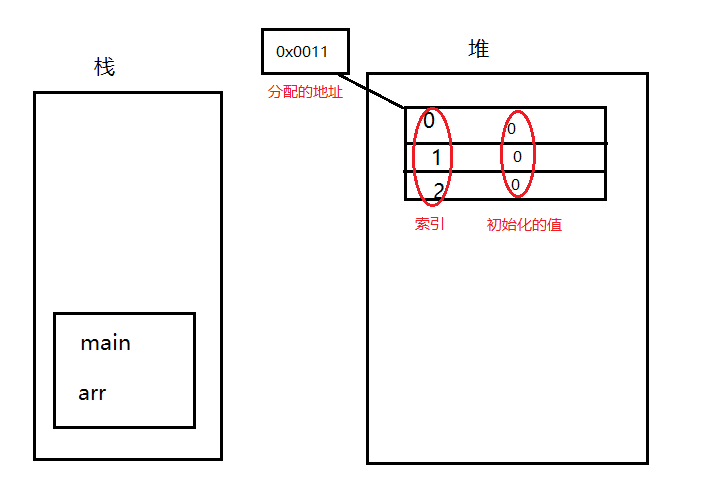
堆和栈的区别(面试经验总结)
C中,内存分为5个区:堆、栈、自由存储区、全局/静态存储区和常量存储区。 栈:是由编译器在需要时自动分配,不需要时自动清除的变量存储区。通常存放局部变量、函数参数等。 堆:是由new分配的内存块,由程序员…

百度Q3财报里的“大生意”
在今日发布的Q3财报中,百度花了不少篇幅来介绍人工智能业务的进展,作为百度的技术核心,近段时间几乎所有百度业务都在与人工智能做深入结合,这预示着移动互联网信息化技术发展已经全面开启人工智能时代,而百度势必要在…

【Codeforces/HDU】76A Plus and xor / 2095 find your present (2)(异或)。
http://codeforces.com/contest/76/problem/D A X Y B X xor Y 异或(不进位加法):两个二进制数,对应的位置上,相同为0,不同为1 性质:a^a0,a^0a,满足交换律 所以…

前端项目如何管理
前端项目如何管理 前端项目的管理分为两个维度:项目内的管理与多项目之间的管理。 1. 项目内的管理 在一个项目内,当有多个开发者一起协作开发时,或者功能越来越多、项目越来越庞大时,保证项目井然有序的进行是相当重要的。 一般会…
CMake学习(一)
什么是 CMake 你或许听过好几种 Make 工具,例如 GNU Make ,QT 的 qmake ,微软的 MS nmake,BSD Make(pmake),Makepp,等等。这些 Make 工具遵循着不同的规范和标准,所执行…

【Codeforces】1104C Grid game (变异的俄罗斯方块)
http://codeforces.com/problemset/problem/1104/C 4 X 4 的方格 放置 1*2的矩形(用1表示)和2*1的矩形(用0表示) 只要有一行或者一列都填满了,就会自动消除,就可以放心的矩形了,只要不重叠就可…

如何创建.gitignore文件,忽略git不必要提交的文件
1、在需要创建 .gitignore 文件的文件夹, 右键选择Git Bash 进入命令行,进入项目所在目录。 2、输入 touch .gitignore ,生成“.gitignore”文件。 3、在”.gitignore” 文件里输入你要忽略的文件夹及其文件就可以了。(注意格式) …

软件安全访谈:ZipSlip、NodeJS安全性和BBS攻击
正如Nodejs Security WG成员和Snyk开发者布道师Liran Tal所写的那样,自BBS早期以来,这种漏洞利用的矢量攻击已经为人所知。InfoQ采访了Tal,了解了更多有关软件安全性(尤其是Nodejs安全性)的相关信息。今年早些时候&…

客户端与服务器的数据交互
毕设需要接粗到一些关于app和前端后端的东西,学习记录一下。 首先不要管安卓端还是苹果端,现在一般都是响应式的app,放到安卓或者苹果或者pc或者平板都是没有问题的。一般采用的是http接口通讯,或者socket连接。具体你要去查资料…

【Codeforces】908B New Year and Buggy Bot(暴力+全排列)
http://codeforces.com/contest/908/problem/B 0 1 2 3 可以对应 上下左右。(具体哪个对应哪个,试过才知道) str 的 长度 为 100,0 1 2 3 的全排列一共24种,最坏的情况可以看成遍历长为2400的字符串,不会…

swoole实现数据库连接池
2019独角兽企业重金招聘Python工程师标准>>> 原生 PHP CURD 让我们来回顾一下PHP中数据库的使用 <?php # curd.php$id 1;$dbh new PDO(); $stmt $dbh->prepare(SELECT * FROM user WHERE id:id); $stmt ->bindValue(:id, $id); $user $stmt->f…

bats-Bash自动化测试工具
本文分析了bats--Bash自动化测试工具的安装、语法、常用指令及常用函数等内容。上篇文章回顾:学习RAID 01/10/10E的区别bats 是一个符合 TAP 标准 的 Bash 版测试框架,它使用了一种极为简便的方法来验证命令行程序是否正常运行。bats 要求 Bash 的最低版…
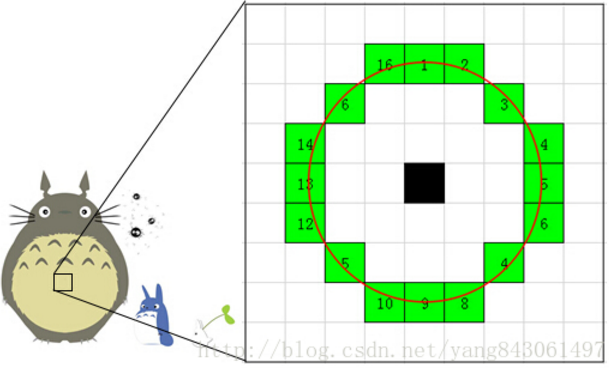
ORB + OPENCV
一、介绍 假如有两张人物图片,我们的目标是要确认这两张图片中的人物是否是同一个人。如果人来判断,这太简单了。但是让计算机来完成这个功能就困难重重。一种可行的方法是: 分别找出两张图片中的特征点描述这些特征点的属性,比较…

【Codeforces】967C Stairs and Elevators (二分)。
http://codeforces.com/contest/967/problem/C 从一个地方到另一个地方,可以选择爬楼梯或者坐电梯 ,前提是楼梯或者电梯存在。 n 楼层数 m 每一层的房间数 s 楼梯的数量 e 电梯的数量 v 电梯的速度 第2行是s个楼梯的位置 第3行是e个电梯的位置 …

webpack 最简打包结果分析
原文链接:https://ssshooter.com/2019-02... 现在的 webpack 不再是入门噩梦,过去 webpack 最让人心塞的莫过于配置文件,而 webpack4 诞生随之而来的是无配置 webpack。 使用 webpack4,至少只需要安装 webpack 和 webpack cli。所以大家完全可…