矩阵奇异值分解简介及C++/OpenCV/Eigen的三种实现
奇异值分解(singular value decomposition, SVD):将矩阵分解为奇异向量(singular vector)和奇异值(singular value)。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每个实数矩阵都有一个奇异值分解,但不一定都有特征分解。例如,非方阵的矩阵没有特征分解,这是我们只能使用奇异值分解。
将矩阵A分解成三个矩阵的乘积:A=UDVT。
假设A是一个m*n的矩阵,那么U是一个m*m的矩阵,D是一个m*n的矩阵,V是一个n*n矩阵。
这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵U和V都被定义为正交矩阵,而矩阵D被定义为对角矩阵。注意,矩阵D不一定是方阵。对角矩阵D对角线上的元素被称为矩阵A的奇异值(singular value)。矩阵U的列向量被称为左奇异向量(left singular vector),矩阵V的列向量被称为右奇异向量(right singular vector)。A的左奇异向量是AAT的特征向量。A的右奇异向量是ATA的特征向量。A的非零奇异值是ATA特征值的平方根,同时也是AAT特征值的平方根。
奇异值分解(singular value decomposition)是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。奇异值分解能够用于任意m*n矩阵,而特征分解只能适用于特定类型的方阵,故奇异值分解的适用范围更广。
以上内容摘自: 《深度学习中文版》 和 维基百科
基于雅克比(Jacobi)方法对矩阵进行奇异值分解操作步骤(参考OpenCV中实现):
(1)、对原始矩阵A(m*n)进行判断,若m<n(即行数小于列数),则交换m、n值;若m≥n,则对A进行转置变换;
(2)、初始化临时变量D、U、Vt:D为奇异值,为n行1列;U为左奇异向量,为m行m列;Vt为转置后的右奇异向量,为n行n列;并初始化D、U、Vt值均为0;
(3)、初始化临时变量A′:A′为m行m列,并将A的值赋值给A′,A′中多余元素赋初值为0;
(4)、由A′、D、Vt开始进行基于Jacobi方法的奇异值分解;
(5)、设置临时变量W,长度为n,将A′中前n行中,每行元素的平方和赋值给W;
(6)、设置Vt为单位矩阵;
(7)、循环计算旋转矩阵,并更新A′、W、Vt对应位置的值;最大循环次数为std::max(m, 30);
(8)、重置W值为A′中前n行,每行元素平方和的开方;
(9)、将W中元素按照从大到小排序,排序后的W即为D中主对角线元素值;
(10)、按照(9)中对W的排序规则对A′和Vt进行排序;
(11)、计算A′中值;
(12)、最终的A′和Vt即为所求的左、右奇异向量。
以下是分别采用C++(参考opencv sources/modules/core/src/lapack.cpp)和OpenCV实现的矩阵奇异值分解:
#include "funset.hpp"
#include <math.h>
#include <iostream>
#include <string>
#include <vector>
#include <opencv2/opencv.hpp>
#include "common.hpp"// ================================= 矩阵奇异值分解 =================================
template<typename _Tp>
static void JacobiSVD(std::vector<std::vector<_Tp>>& At,std::vector<std::vector<_Tp>>& _W, std::vector<std::vector<_Tp>>& Vt)
{double minval = FLT_MIN;_Tp eps = (_Tp)(FLT_EPSILON * 2);const int m = At[0].size();const int n = _W.size();const int n1 = m; // urowsstd::vector<double> W(n, 0.);for (int i = 0; i < n; i++) {double sd{0.};for (int k = 0; k < m; k++) {_Tp t = At[i][k];sd += (double)t*t;}W[i] = sd;for (int k = 0; k < n; k++)Vt[i][k] = 0;Vt[i][i] = 1;}int max_iter = std::max(m, 30);for (int iter = 0; iter < max_iter; iter++) {bool changed = false;_Tp c, s;for (int i = 0; i < n - 1; i++) {for (int j = i + 1; j < n; j++) {_Tp *Ai = At[i].data(), *Aj = At[j].data();double a = W[i], p = 0, b = W[j];for (int k = 0; k < m; k++)p += (double)Ai[k] * Aj[k];if (std::abs(p) <= eps * std::sqrt((double)a*b))continue;p *= 2;double beta = a - b, gamma = hypot_((double)p, beta);if (beta < 0) {double delta = (gamma - beta)*0.5;s = (_Tp)std::sqrt(delta / gamma);c = (_Tp)(p / (gamma*s * 2));} else {c = (_Tp)std::sqrt((gamma + beta) / (gamma * 2));s = (_Tp)(p / (gamma*c * 2));}a = b = 0;for (int k = 0; k < m; k++) {_Tp t0 = c*Ai[k] + s*Aj[k];_Tp t1 = -s*Ai[k] + c*Aj[k];Ai[k] = t0; Aj[k] = t1;a += (double)t0*t0; b += (double)t1*t1;}W[i] = a; W[j] = b;changed = true;_Tp *Vi = Vt[i].data(), *Vj = Vt[j].data();for (int k = 0; k < n; k++) {_Tp t0 = c*Vi[k] + s*Vj[k];_Tp t1 = -s*Vi[k] + c*Vj[k];Vi[k] = t0; Vj[k] = t1;}}}if (!changed)break;}for (int i = 0; i < n; i++) {double sd{ 0. };for (int k = 0; k < m; k++) {_Tp t = At[i][k];sd += (double)t*t;}W[i] = std::sqrt(sd);}for (int i = 0; i < n - 1; i++) {int j = i;for (int k = i + 1; k < n; k++) {if (W[j] < W[k])j = k;}if (i != j) {std::swap(W[i], W[j]);for (int k = 0; k < m; k++)std::swap(At[i][k], At[j][k]);for (int k = 0; k < n; k++)std::swap(Vt[i][k], Vt[j][k]);}}for (int i = 0; i < n; i++)_W[i][0] = (_Tp)W[i];srand(time(nullptr));for (int i = 0; i < n1; i++) {double sd = i < n ? W[i] : 0;for (int ii = 0; ii < 100 && sd <= minval; ii++) {// if we got a zero singular value, then in order to get the corresponding left singular vector// we generate a random vector, project it to the previously computed left singular vectors,// subtract the projection and normalize the difference.const _Tp val0 = (_Tp)(1. / m);for (int k = 0; k < m; k++) {unsigned int rng = rand() % 4294967295; // 2^32 - 1_Tp val = (rng & 256) != 0 ? val0 : -val0;At[i][k] = val;}for (int iter = 0; iter < 2; iter++) {for (int j = 0; j < i; j++) {sd = 0;for (int k = 0; k < m; k++)sd += At[i][k] * At[j][k];_Tp asum = 0;for (int k = 0; k < m; k++) {_Tp t = (_Tp)(At[i][k] - sd*At[j][k]);At[i][k] = t;asum += std::abs(t);}asum = asum > eps * 100 ? 1 / asum : 0;for (int k = 0; k < m; k++)At[i][k] *= asum;}}sd = 0;for (int k = 0; k < m; k++) {_Tp t = At[i][k];sd += (double)t*t;}sd = std::sqrt(sd);}_Tp s = (_Tp)(sd > minval ? 1 / sd : 0.);for (int k = 0; k < m; k++)At[i][k] *= s;}
}// matSrc为原始矩阵,支持非方阵,matD存放奇异值,matU存放左奇异向量,matVt存放转置的右奇异向量
template<typename _Tp>
int svd(const std::vector<std::vector<_Tp>>& matSrc,std::vector<std::vector<_Tp>>& matD, std::vector<std::vector<_Tp>>& matU, std::vector<std::vector<_Tp>>& matVt)
{int m = matSrc.size();int n = matSrc[0].size();for (const auto& sz : matSrc) {if (n != sz.size()) {fprintf(stderr, "matrix dimension dismatch\n");return -1;}}bool at = false;if (m < n) {std::swap(m, n);at = true;}matD.resize(n);for (int i = 0; i < n; ++i) {matD[i].resize(1, (_Tp)0);}matU.resize(m);for (int i = 0; i < m; ++i) {matU[i].resize(m, (_Tp)0);}matVt.resize(n);for (int i = 0; i < n; ++i) {matVt[i].resize(n, (_Tp)0);}std::vector<std::vector<_Tp>> tmp_u = matU, tmp_v = matVt;std::vector<std::vector<_Tp>> tmp_a, tmp_a_;if (!at)transpose(matSrc, tmp_a);elsetmp_a = matSrc;if (m == n) {tmp_a_ = tmp_a;} else {tmp_a_.resize(m);for (int i = 0; i < m; ++i) {tmp_a_[i].resize(m, (_Tp)0);}for (int i = 0; i < n; ++i) {tmp_a_[i].assign(tmp_a[i].begin(), tmp_a[i].end());}}JacobiSVD(tmp_a_, matD, tmp_v);if (!at) {transpose(tmp_a_, matU);matVt = tmp_v;} else {transpose(tmp_v, matU);matVt = tmp_a_;}return 0;
}int test_SVD()
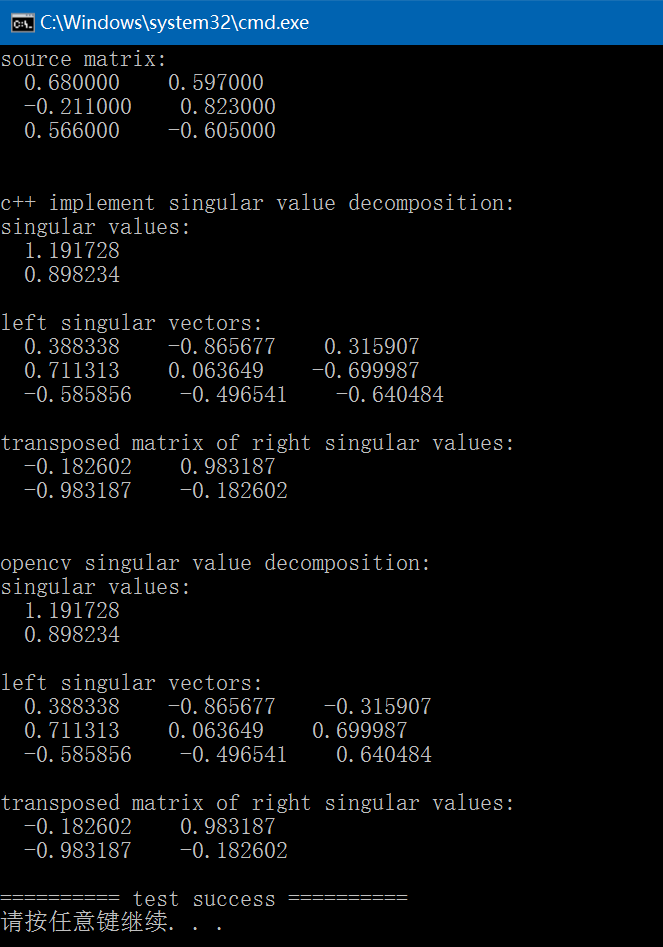
{//std::vector<std::vector<float>> vec{ { 1.2f, 2.5f, 5.6f, -2.5f },// { -3.6f, 9.2f, 0.5f, 7.2f },// { 4.3f, 1.3f, 9.4f, -3.4f },// { 6.4f, 0.1f, -3.7f, 0.9f } };//const int rows{ 4 }, cols{ 4 };//std::vector<std::vector<float>> vec{ { 1.2f, 2.5f, 5.6f, -2.5f },// { -3.6f, 9.2f, 0.5f, 7.2f },// { 4.3f, 1.3f, 9.4f, -3.4f } };//const int rows{ 3 }, cols{ 4 };std::vector<std::vector<float>> vec{ { 0.68f, 0.597f },{ -0.211f, 0.823f },{ 0.566f, -0.605f } };const int rows{ 3 }, cols{ 2 };fprintf(stderr, "source matrix:\n");print_matrix(vec);fprintf(stderr, "\nc++ implement singular value decomposition:\n");std::vector<std::vector<float>> matD, matU, matVt;if (svd(vec, matD, matU, matVt) != 0) {fprintf(stderr, "C++ implement singular value decomposition fail\n");return -1;}fprintf(stderr, "singular values:\n");print_matrix(matD);fprintf(stderr, "left singular vectors:\n");print_matrix(matU);fprintf(stderr, "transposed matrix of right singular values:\n");print_matrix(matVt);fprintf(stderr, "\nopencv singular value decomposition:\n");cv::Mat mat(rows, cols, CV_32FC1);for (int y = 0; y < rows; ++y) {for (int x = 0; x < cols; ++x) {mat.at<float>(y, x) = vec.at(y).at(x);}}/*w calculated singular valuesu calculated left singular vectorsvt transposed matrix of right singular vectors*/cv::Mat w, u, vt, v;cv::SVD::compute(mat, w, u, vt, 4);//cv::transpose(vt, v);fprintf(stderr, "singular values:\n");print_matrix(w);fprintf(stderr, "left singular vectors:\n");print_matrix(u);fprintf(stderr, "transposed matrix of right singular values:\n");print_matrix(vt);return 0;
} 以下是采用Eigen实现的矩阵奇异值分解code:
#include "funset.hpp"
#include <math.h>
#include <iostream>
#include <vector>
#include <string>
#include <opencv2/opencv.hpp>
#include <Eigen/Dense>
#include "common.hpp"int test_SVD()
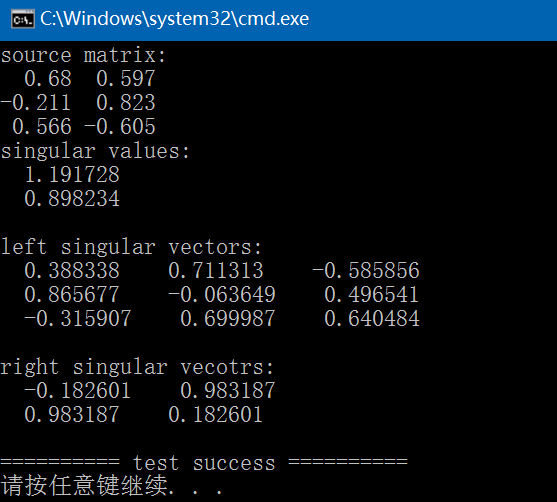
{//std::vector<std::vector<float>> vec{ { 1.2f, 2.5f, 5.6f, -2.5f },// { -3.6f, 9.2f, 0.5f, 7.2f },// { 4.3f, 1.3f, 9.4f, -3.4f },// { 6.4f, 0.1f, -3.7f, 0.9f } };//const int rows{ 4 }, cols{ 4 };//std::vector<std::vector<float>> vec{ { 1.2f, 2.5f, 5.6f, -2.5f },// { -3.6f, 9.2f, 0.5f, 7.2f },// { 4.3f, 1.3f, 9.4f, -3.4f } };//const int rows{ 3 }, cols{ 4 };std::vector<std::vector<float>> vec{ { 0.68f, 0.597f },{ -0.211f, 0.823f },{ 0.566f, -0.605f } };const int rows{ 3 }, cols{ 2 };std::vector<float> vec_;for (int i = 0; i < rows; ++i) {vec_.insert(vec_.begin() + i * cols, vec[i].begin(), vec[i].end());}Eigen::Map<Eigen::Matrix<float, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> m(vec_.data(), rows, cols);fprintf(stderr, "source matrix:\n");std::cout << m << std::endl;Eigen::JacobiSVD<Eigen::MatrixXf> svd(m, Eigen::ComputeFullV | Eigen::ComputeFullU); // ComputeThinU | ComputeThinVEigen::MatrixXf singular_values = svd.singularValues();Eigen::MatrixXf left_singular_vectors = svd.matrixU();Eigen::MatrixXf right_singular_vectors = svd.matrixV();fprintf(stderr, "singular values:\n");print_matrix(singular_values.data(), singular_values.rows(), singular_values.cols());fprintf(stderr, "left singular vectors:\n");print_matrix(left_singular_vectors.data(), left_singular_vectors.rows(), left_singular_vectors.cols());fprintf(stderr, "right singular vecotrs:\n");print_matrix(right_singular_vectors.data(), right_singular_vectors.rows(), right_singular_vectors.cols());return 0;
}由以上结果可见:C++、OpenCV、Eigen结果是相同的。
GitHub:
https://github.com/fengbingchun/NN_Test
https://github.com/fengbingchun/Eigen_Test
相关文章:

经典!工业界深度推荐系统与CTR预估必读的论文汇总
(图片付费下载自视觉中国)来源 | 深度传送门(ID: gh_5faae7b50fc5)导读:本文是“深度推荐系统”专栏的第十一篇文章,这个系列将介绍在深度学习的强力驱动下,给推荐系统工业界所带来的最前沿的变…

docker上传自己的镜像
https://blog.csdn.net/boonya/article/details/74906927 需要注意的就是命名规范 docker push 注册用户名/镜像名 tag命令修改为规范的镜像: docker tag boonya/tomcat-allow-remote boonyadocker/tomcat-allow-remote转载于:https://www.cnblogs.com/MC-Curry/p/1…

多个class相同的input标签 获取当前值!方法!
2019独角兽企业重金招聘Python工程师标准>>> var a $(this).prev( ".你的class" ).val(); 转载于:https://my.oschina.net/u/1169079/blog/210082

C++11中std::forward_list单向链表的使用
std::forward_list是在C11中引入的单向链表或叫正向列表。forward_list具有插入、删除表项速度快、消耗内存空间少的特点,但只能向前遍历。与其它序列容器(array、vector、deque)相比,forward_list在容器内任意位置的成员的插入、提取(extracting)、移动…

即学即用的30段Python实用代码
(图片付费下载自视觉中国)原标题 | 30 Helpful Python Snippets That You Can Learn in 30 Seconds or Less作 者 | Fatos Morina翻 译 | Pita & AI开发者Python是目前最流行的语言之一,它在数据科学、机器学习、web开发、脚本编写、自…
如何配置IntelliJ IDEA发布JavaEE项目?
一、以war的形式运行项目 步骤1 新建或者导入项目后,选择File菜单-》Project Structure...,如下图: 步骤2 配置项目类型,名字可以自定义: 说明:这里的Artifact如果没有配置好的话,配置Tomcat时没…

网络分布式软件bonic清除
近期,有一款网格计算软件,在很多服务器上进行了部署,利用cpu进行运算。虽然未构成安全隐患,但是比较消耗资源,影响设备正常运行。今天对设备彻底检查,发现了一个分布式计算软件boinc,他是利用网…

C++/C++11中std::list双向链表的使用
std::list是双向链表,是一个允许在序列中任何一处位置以常量耗时插入或删除元素且可以双向迭代的顺序容器。std::list中的每个元素保存了定位前一个元素及后一个元素的信息,允许在任何一处位置以常量耗时进行插入或删除操作,但不能进行直接随…

React组件设计之边界划分原则
简述 结合SOLID中的单一职责原则来进行组件的设计 Do one thing and do it well javaScript作为一个弱类型并在函数式和面对对象的领域里疯狂试探语言。SOLID原则可能与其他语言例如(java)的表现可能是不同的。不过作为软件开发领域通用的原则࿰…

阿里AI labs发布两大天猫精灵新品,将与平头哥共同定制智能语音芯片
作者 | 夕颜出品 | AI科技大本营(ID:rgznai100)2019 年,去年刮起的一阵智能音箱热浪似乎稍微冷却下来,新产品不再像雨后春笋一样层出不穷,挺过市场洗礼的产品更是凤毛麟角,这些产品的性能、技术支持和体验基…

js 中文匹配正则
为什么80%的码农都做不了架构师?>>> /^[\u4e00-\u9fa5]{2,4}$/gi.test() 匹配中文正则 转载于:https://my.oschina.net/fedde/blog/211852

Caffe中对cifar10执行train操作
参考Caffe source中examples/cifar10目录下内容。cifar10是一个用于普通物体识别的数据集,cifar10被分为10类,分别为airplane、automobile、bird、cat、deer、dog、frog、horse、ship、truck,关于cifar10的详细介绍可以参考: http://blog.csd…

解决掉这些痛点和难点,让知识图谱不再是“噱头”
(图片付费下载自视觉中国)作者| 夕颜出品| AI科技大本营(ID:rgznai100)2012 年,谷歌正式提出知识图谱的概念,当时,研究人员的主要目的是用来优化搜索引擎技术。今年初,谷歌前员工&am…

mongodb使用常用语法,持续更新
设置快捷命令D:\mongodb4.0.8\bin>mongod --config "D:\mongodb4.0.8\mongo.conf" --auth --install --serviceName "MongoDB"mongodb配置文件#数据库路径dbpathD:\mongodb4.0.8\data\db#日志输出文件路径logpathD:\mongodb4.0.8\data\log\MongoDB.log#…

Android之NDK开发的简单实例
NDK全称为Native Development Kit,是本地开发工具集。在Android开发中,有时为了能更好的重用以前的C/C的代码,需要将这些代码编译成相应的so,然后通地JNI以供上层JAVA调用。当然,也有的是为了更高的保护性和安全性。下…

阿里披露AI完整布局,飞天AI平台首次亮相
作者 | 夕颜编辑 | 唐小引出品 | AI 科技大本营(ID:rgznai100)9 月 26 日上午,在云栖大会阿里云飞天智能主论坛上,年轻的阿里巴巴副总裁、阿里云智能计算平台事业部总经理、高级研究员贾扬清与其在 Facebook 的老同事—— Faceboo…
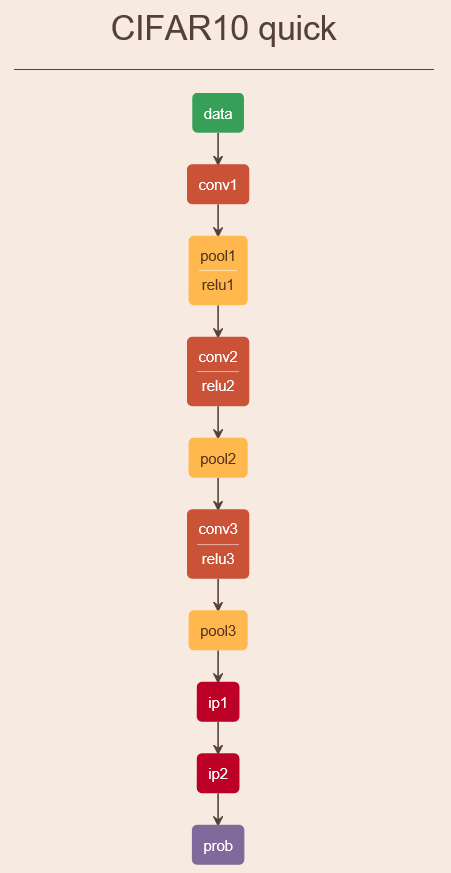
使用Caffe基于cifar10进行物体识别
在http://blog.csdn.net/fengbingchun/article/details/72953284中对cifar10进行train,这里通过train得到的model,对图像进行识别。cifar10数据集共包括10类,按照0到9的顺序依次为airplane(飞机)、automobile(轿车)、bird(鸟)、cat(猫)、deer…

SoJpt Boot 2.3-3.8 发布,Spring Boot 使用 Jfinal 特性极速开发
SoJpt Boot 2.3-3.8 发布了。SoJpt Boot 基于 JFinal 与 Spring Boot制作, 实现了 Spring Boot 与 Jfinal 的混合双打,使 Spring Boot 下的开发者能够体验 Jfinal 的极速开发特性。新版更新内容如下: SoJpt-Boot-2.3-3.8 changelog 1、加入事务注解,Tx(value"c…

PL/SQL程序设计 第七章 包的创建和应用
7.1 引言包是一组相关过程、函数、变量、常量和游标等PL/SQL程序设计元素的组合,它具有面向对象程序设计语言的特点,是对这些PL/SQL 程序设计元素的封装。包类似于C和JAVA语言中的类,其中变量相当于类中的成员变量,过程和函数相当…

C++11中头文件chrono的使用
在C11中,<chrono>是标准模板库中与时间有关的头文件。该头文件中所有函数与类模板均定义在std::chrono命名空间中。 std::chrono是在C11中引入的,是一个模板库,用来处理时间和日期的Time library。要使用chrono库,需要incl…

为什么平头哥做芯片如此迅猛?
作者 | 胡巍巍 发自杭州云栖大会责编 | 唐小引来源 | CSDN(ID:CSDNnews)2018年10月31日,阿里旗下的平头哥半导体有限公司成立。如今,平头哥成立不到一年,就已成绩斐然。2019年9月25日,阿里巴巴旗…

Vue 组件库 heyui@1.18.0 发布,新增地址选择、图片预览组件
开发四年只会写业务代码,分布式高并发都不会还做程序员? 新增 CategoryPicker 新增组件 CategoryPicker,地址级联组件的最佳方案。 <CategoryPicker :option"option" v-model"value"/> 相关文档 ImagePreview 新…

HTML5 Dashboard – 那些让你激动的 Web 技术
HTML5 Dashboard 是一个 Mozilla 推出的项目,里面展示了最前沿的 HTML5,CSS3,JavaScript 技术。每一项技术都有简洁,在线演示以及详细的文档链接。这些技术将成为未来一段时间 Web 开发的顶尖技术,如果不想落伍的话就赶…

计算机解决问题没有奇技淫巧,但动态规划还是有点套路
作者 | labuladong来源 | labuladong(ID:labuladong) 【导读】动态规划算法似乎是一种很高深莫测的算法,你会在一些面试或算法书籍的高级技巧部分看到相关内容,什么状态转移方程,重叠子问题,最优子结构等高…

idea下,Jetty采用main方法启动web项目
为什么80%的码农都做不了架构师?>>> 对于maven多模块的spring web项目,本地开发时,启动的方式一般有如下几种: 使用容器(tomcat/jetty/resin等),该方式需要ide支持,而社…
概率论中均值、方差、标准差介绍及C++/OpenCV/Eigen的三种实现
概率论是用于表示不确定性声明(statement)的数学框架。它不仅提供了量化不确定性的方法,也提供了用于导出新的不确定性声明的公理。在人工智能领域,概率论主要有两种用途。首先,概率法则告诉我们AI系统如何推理,据此我们设计一些算…

[转]CentOS 5.5下FTP安装及配置
一、FTP的安装 1、检测是否安装了FTP : [rootlocalhost ~]# rpm -q vsftpd vsftpd-2.0.5-16.el5_5.1 否则显示:[rootlocalhost ~]# package vsftpd is not installed 查看ftp运行状态 service vsftpd status 2、如果没安装FTP,运行yum install vsftpd命令进行安装 如…

C++11中头文件thread的使用
C11中加入了<thread>头文件,此头文件主要声明了std::thread线程类。C11的标准类std::thread对线程进行了封装。std::thread代表了一个线程对象。应用C11中的std::thread便于多线程程序的移值。 <thread>是C标准程序库中的一个头文件,定义了…

python3 urllib 类
urllib模块中的方法 1.urllib.urlopen(url[,data[,proxies]]) 打开一个url的方法,返回一个文件对象,然后可以进行类似文件对象的操作。本例试着打开google >>> import urllib >>> f urllib.urlopen(http://www.google.com.hk/) >&…
阿里飞天大数据飞天AI平台“双生”系统正式发布,9大全新数据产品集中亮相
作者 | 夕颜 责编 | 唐小引 出品 | AI科技大本营(ID:rgznai100) 如今,大数据和 AI 已经成为两个分不开的词汇,没有大数据,AI 就失去了根基;没有 AI,数据不会呈现爆发式的增长。如何将 AI 与大…