AI芯片初创公司单纯卖芯片还是捆绑算法的商业模式更好?...
雷锋网在《资本寒冬,这样的AI芯片公司2019年危矣》一文中已经提到,2019年的资本寒冬以及整个半导体行业的低迷,将会让那些没有技术独特性以及缺乏商业落地能力,且现金流控制不好的AI芯片公司面临巨大的挑战,甚至大概率会倒下。
因此,AI芯片在2019年落地的重要性已经毋庸置疑,那么,对于AI芯片公司,接下来关键问题就是如何在2019年实现产品的规模商用?哪种商业模式是更好的选择?

【 图片来源:alltechasia 】
芯片公司的商业模式
芯片不仅是一个技术密集、资本密集、人才密集的高门槛行业,同样也是产业链很长的行业。在这条很长的产业链里,仅芯片公司,也有着不同的盈利模式。
比如我们熟知的英特尔和AMD,用户可以直接购买其芯片,高通则为手机厂商提供芯片,英特尔、AMD和高通取得的成绩也证明了这一商业模式的成功。除了卖芯片,IP授权的模式也成就了一些芯片公司,典型的例子就是Arm,Arm靠提供芯片的知识产权发家,凭借着与英特尔的差异化竞争,Arm架构的芯片如今已经搭载在了大部分的移动智能设备中。还有如今AI芯片领域的代表英伟达,英伟达最早也出售芯片,后来慢慢转变为卖GPU卡。
到了AI时代,我们已经看到不同的AI芯片公司也在用不同的商业模式探索AI芯片的落地。AI IP公司典型的就是AI独角兽公司寒武纪,并且寒武纪IP落地已经有成功案例,其IP搭载在麒麟970和麒麟980的SoC中。
不过,在AI时代的AI芯片公司似乎更倾向于提供AI加速卡以及相关的服务。雷锋网此前报道,在华为AI芯片发布会后的采访中,华为轮值董事长徐直军多次强调,华为昇腾910和310芯片将不会对外单独销售,而是以AI加速卡、加速模块、服务器和一体机等模式对外销售。另外,比特大陆、云天励飞等拥有AI芯片的公司也都更倾向于提供模块化的方案。

【 图片来源:smart2zero 】
到底选择哪种商业模式更好?
这是否意味着一体化的方案更适合AI芯片初创公司?探境科技CEO鲁勇接受采访时表示,AI芯片相较于传统芯片的特点是多了算法,这意味着AI芯片这样软硬结合的产品,单独出售芯片可能无法工作,而AI算法也是一个稀缺资源,所以将算法和芯片捆绑作为一体化的方案也就成了许多公司的想法。
鲁勇同时指出,客户的需求多种多样,有的只需要芯片,而有的则需要同时需要芯片和算法。不同的AI芯片公司会根据自身的特点选择合适的商业模式,这不能只看表面,要看其实质。因此,到底哪种方式更适合不能一概而论,商业是多种多样的。
据了解,探境既可以单独提供芯片,也可以提供软硬一体的方案。至于是否会卖IP,鲁勇表示从Arm的经验和营收看,这并不会是探境优先选择的方式。
以算法见长,在本月初发布AI语音芯片的思必驰同样会根据市场的需求提供芯片。思必驰CTO/深聪智能CEO周伟达接受雷锋网(公众号:雷锋网)专访时表示:“如果客户希望从我们这里采购马上就能满足他们应用的方案,我们可以提供Turnkey的方案。但对于那些拥有自己开发团队,也对芯片硬件平台比较了解的团队,我们也可以只提供芯片。根据客户的需求和他们判断,思必驰以比较开放的心态根据市场的需求来提供不同的产品。”
地平线联合创始人、算法副总裁黄畅认为:“AI芯片的大规模商用需要产生围绕AI芯片的杀手级应用,我们认为新的杀手级应用可能来自智能IoT场景、智能驾驶场景。聚焦这些场景,软硬结合、深度优化、协同设计,将最大限度地提升性能、为客户创造最大的价值。同时,AI应用场景非常丰富,构建开放的平台,在AI芯片上提供丰富的软件、有力的服务,赋能客户在AI芯片上开发出来更多、更丰富的应用,则可以在更广大的长尾场景上为AI落地创造机会。”
鲲云科技创始人兼CEO牛昕宇表示:“实现AI芯片规模商用的核心点在于找到满足客户需求的差异化优势,这个对于每家公司都一样。”
至于直接提供芯片还是一体化方案更好的问题,牛昕宇认为,一体化方案是差异化竞争的一种方式,因为目标客户从方案公司变为了终端用户。一体化方案与单纯卖芯片一样,都是实现商业化的手段,提供一体化方案要考虑如何发挥自己的芯片优势、长期的竞争优势如何建立等;提供芯片要考虑如何快速落地实现规模化拓展以及如何把使用门槛降低,这是对于市场的不同切入角度,没有优劣之分。
雷锋网小结
2019年对AI芯片初创公司而言无疑是一个巨大的考验,AI芯片公司拥有技术独特性确实是其保持竞争力的重要部分,不过从目前的情况看大多数公司都在进行FMA(浮点乘法累加)和混合精度数学(整型8位和浮点16位和32位)的工作,这是更容易获得成果的方法。
因此,AI芯片落地的商业模式的选择也十分重要。需要看到,芯片公司无论是提供芯片还是一体化的方案,都要根据公司自身的特点,结合客户的需求提供更具性价比的方案,才能获得用户任认可实现芯片的更快落地。
还需看到的是,AI芯片的软硬一体化也将让硬件团队和软件团队进行跟紧密的协作,这也是AI芯片在规模落地过程中需要面对的问题。
相关文章:
芯片巨头们2019年的AI芯片之争会如何?
2018年全球最值得关注的AI芯片初创公司
资本寒冬,这样的AI芯片公司2019年危矣
相关文章:
VS2017配置OpenCV3.2+contrib3.2
VS2017配置OpenCV3.2contrib3.2前言opecv3.2opencv_contrib3.2模块都编译配置了在配置contrib之前,尝试直接配置OpeCV3.2-vc14,发现可以正常使用,也就是说官方包虽然只有vc14,但vs2017(vc15)也支持的很好。操作环境:WIN10 64bit &…
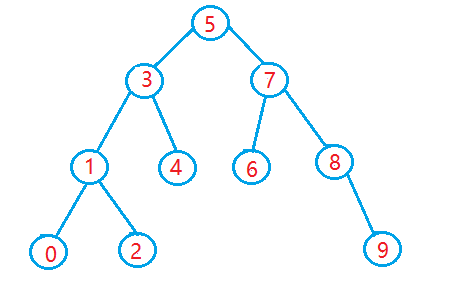
【ACM】二叉搜索树(Binary Search Tree /BS Tree) 小结
动态管理集合的数据结构——二叉搜索树 搜索树是一种可以进行插入,搜索,删除等操作的数据结构,可以用字典或者优先队列。 二叉排序树又称为二叉查找树,他或者为空树,或者是满足如下性质的二叉树。 (1&…

android安卓动态设置控件宽高
LayoutParams layoutParamsp_w_picpathView.getLayoutParams();layoutParams.width100;layoutParams.height200;p_w_picpathView.setLayoutParams(layoutParams);转载于:https://blog.51cto.com/11020803/1860242

《深入java虚拟机》读书笔记类加载
概述 类加载机制是指虚拟机将描述类的数据从Class文件中加载到内存,并进行数据验证、解析、初始化等过程,最后形成可以直接被虚拟机使用的java类型。在java语言中类的加载、链接、初始化等过程并不是在编译时期完成,而是在运行时期才进行的&a…

SLAM之特征匹配(一)————RANSAC-------OpenCV中findFundamentalMat函数使用的模型
目录 1.RANSAC原理 2. RANSAC算法步骤: 3. RANSAC源码解析 step one niters最初的值为2000,这就是初始时的RANSAC算法的循环次数,getSubset()函数是从一组对应的序列中随机的选出4组(因为要想计算出一…

I hope so 2016-Oct-10
2019独角兽企业重金招聘Python工程师标准>>> <I hope so> - A joke A: Do you think your son will forget all he learned at college? B: I hopse so. He certainly cant make a living by kissing girls! 转载于:https://my.oschina.net/u/553266/blog/75…

【Codeforces】158B-Taxi(贪心,怎么贪咧)
贪心 emmmm http://codeforces.com/contest/158/problem/B 题目大意:有四种旅客,四人一组,三人一组,两人一组,一人一组,一辆出租车最多可以坐四个人,并且一组里的人必须坐一辆车,…

90 后 CTO 创业 6 年,做了一件改变互联网的“小事”
TGO 鲲鹏会在武汉举行了一场线下分享活动 —— 冲破壁垒,打造精英的技术团队 。来自极验的 90 后 CTO 黄胜蓝分享了他的团队故事,以及在他看来一个创新团队应该具备的特征。极验 CTO \u0026 TGO 鲲鹏会会员黄胜蓝在现场进行分享 1. 创新:非典…
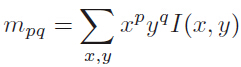
ORB特征(二)
为了满足实时性的要求,前面文章中介绍过(具体链接如下)快速提取特征点算法Fast,以及特征描述子Brief。本篇文章介绍的ORB算法结合了Fast和Brief的速度优势,并做了改进,且ORB是免费Ethan Rublee等人2011年在《ORB&#…

【POJ】2377 Bad Cowtractors(最大生成树)
简单题,模板题 求解最大生成树,提交一直WA,感觉没有什么问题啊,就是在求解最小生成树的模板基础上稍加修改即可,后来发现在输出a,b,c给map二维数组的时候还必须有判断条件,略为有点…

使用let替换var实现块级作用域的小发现
在讲述javascript没有块级作用域的时候都会提到一个非常经典的例子: var obj{name:helo,age:15 }; var arr[];for(var i0;i<5;i){arr[i]i;console.log(i);} console.log(arr); console.log(i);因为javascript没有块级作用域,所以控制台打印出来的结果…

windows系统下node、npm的安装和卸载
Greta有话说:我是在有道云笔记只弄个记录的笔记,粘贴过来之后,没有图片,我的笔记地址为: 有道云笔记,请点我 一、卸载 1、node.js、nvm、 npm (1)在cmd中输入where node找到node…
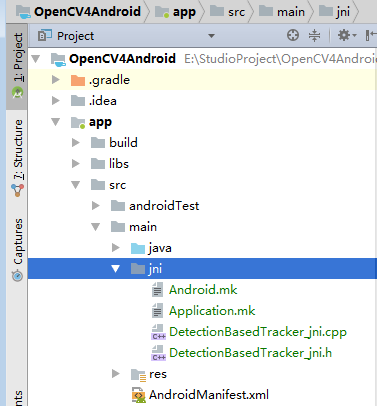
OpenCV4Android开发实录(2): 使用OpenCV3.4.1库实现人脸检测
OpenCV4Android开发实录(2): 使用OpenCV3.3.0库实现人脸检测 转载请声明出处:http://write.blog.csdn.net/postedit/78992490OpenCV4Android系列: 1. OpenCV4Android开发实录(1):移植OpenCV3.3.0库到Android Studio 2.OpenCV4Andr…

活动|跟着微软一起,拥抱开源吧!
由开源社主办的中国开源年会2016 (COSCon16 - China Open Source Conference 2016) 即将于今年10月15日-16日在北京举办。微软大咖将为您呈现区块链,容器,大数据,Xamarin等时下热点技术,参会者还可获取价值1,500 元 Azure 服务使用…

【HDU/算法】最短路问题 杭电OJ 2544 (Dijkstra,Dijkstra+priority_queue,Floyd,Bellman_ford,SPFA)
最短路径问题是图论中很重要的问题。 解决最短路径几个经典的算法 1、Dijkstra算法 单源最短路径(贪心),还有用 priority_queue 进行优化的 Dijkstra 算法。 2、bellman-ford算法 例题:【ACM】POJ 3259 Wormholes 允许负权边…

javaSE基础知识 1.5整数类型
整数的四种声明类型它们分别是,byte,short,int,long,这四种类型所占用的空间是不同的byte是占用1个字节,它的取值范围是 -128~127,short是占用2个字节,他的取值范围是-32768~32767&a…

源码分析-GLSurfaceView的内部实现
GLSurfaceView类是继承自SurfaceView的,并且实现了SurfaceHolder.Callback2接口。GLSurfaceView内部管理着一个surface,专门负责OpenGL渲染。GLSurfaceView内部通过GLThread和EGLHelper为我们完成了EGL环境渲染和渲染线程的创建及管理,使我们…

【POJ/算法】 3259 Wormholes(Bellman-Ford算法, SPFA ,FLoyd算法)
Bellman-Ford算法 Bellman-Ford算法的优点是可以发现负圈,缺点是时间复杂度比Dijkstra算法高。而SPFA算法是使用队列优化的Bellman-Ford版本,其在时间复杂度和编程难度上都比其他算法有优势。 Bellman-Ford算法流程分为三个阶段: 第一步&am…
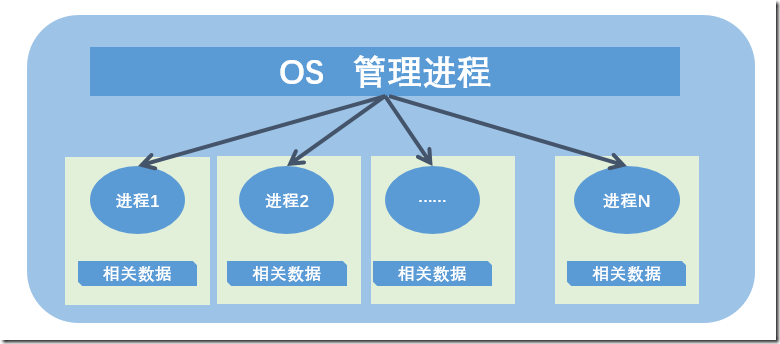
进程控制概念简介 多线程上篇(三)
进程控制 进程的基本数据信息是操作系统控制管理进程的数据集合,这些信息就是用来控制进程的,此处我们说的进程控制就是进程的管理。比如进程有状态,那么进程的创建、终止,状态的切换,这都不是进程自主进行的ÿ…

Android OpenGL使用GLSurfaceView预览视频
Android OpenGL使用GLSurfaceView预览视频第一章 相关知识介绍在介绍具体的功能之前,先对一些主要的类和方法进行一些介绍,这样可以更好的理解整个程序1.1 GLSurfaceView在谷歌的官方文档中是这样解释GLSurfaceView的:An implementation of S…

【Android 基础】Animation 动画介绍和实现
转载自:http://www.cnblogs.com/yc-755909659/p/4290114.html1.Animation 动画类型Android的animation由四种类型组成:XML中alph渐变透明度动画效果scale渐变尺寸伸缩动画效果translate画面转换位置移动动画效果rotate画面转移旋转动画效果JavaCode中Alp…

【Codeforces】1111B - Average Superhero Gang Power
http://codeforces.com/problemset/problem/1111/B n 表示要输入的数据的个数 k 最每一个数据最多可以进行多少次操作 m 一共可以进行多少次操作 一次操作:删除这个数,或者给这个数加1 如果n为1的话,那么只要找出m和k的最小值加到那个数…

刷前端面经笔记(七)
1.描述一下渐进增强和优雅降级 优雅降级(graceful degradation):一开始就构建站点的完整功能,然后针对浏览器测试和修复。渐进增强(progressive enhancement):一开始只构建站点的最少特性,然后不断针对各浏览器追加功能。 2.为什么…

AR资料与连接梳理
AR引擎相关技术 ------------------------------ ARcore:https://developers.google.cn/ar/discover/ ARkit:https://developer.apple.com/arkit/ 以上重点关注,比较新有一些新的功能大家可以自行体验。 ARToolkithttp://www.artoolkit.orght…

Queues 队列
1. Definiation What is a queue? A queue is a list. With a queue, inseration is done at one end (known as rear) whereas deletion is performed at the other end (known as front). 2. Operations 指针对列 无法自定义队长 // array queue #include<iostream> u…

【HDU】1005 Number Sequence (有点可爱)
http://acm.hdu.edu.cn/showproblem.php?pid1005 A number sequence is defined as follows: f(1) 1, f(2) 1, f(n) (A * f(n - 1) B * f(n - 2)) mod 7. Given A, B, and n, you are to calculate the value of f(n). 直接递归求解f(n)的话,会MLE 在计算…

CNCF案例研究:奇虎360
公司:奇虎360地点:中国北京行业:计算机软件 挑战 中国软件巨头奇虎360科技的搜索部门,so.com是中国第二大搜索引擎,市场份额超过35%。该公司一直在使用传统的手动操作来部署环境,随着项目数量的…

C#代码实现对Windows凭据的管理
今天有个任务,那就是使用C#代码实现对windows凭据管理的操作。例如:向windows凭据管理中添加凭据、删除凭据以及查询凭据等功能。于是乎,就开始在网上查找。经过漫长的查询路,终于在一片英文博客中找到了相关代码。经过实验&#…

Android:JNI 与 NDK到底是什么
前言 在Android开发中,使用 NDK开发的需求正逐渐增大但很多人却搞不懂 JNI 与 NDK 到底是怎么回事今天,我将先介绍JNI 与 NDK & 之间的区别,手把手进行 NDK的使用教学,希望你们会喜欢 目录 1. JNI介绍 1.1 简介 定义&…
【ACM】LightOJ - 1008 Fibsieve`s Fantabulous Birthday (找规律,找...)
https://vjudge.net/problem/LightOJ-1008 题目很好理解,第一行表示测试样例的个数,接下来输入一个大于等于1的数,按照格式输出这个数的坐标 蓝色的是 奇数的平方; 红色的是 偶数的平方; 黄色的是对角线:…
