SLAM十四讲笔记1
文章目录
- ch02 初识SLAM
- ch02-01 经典视觉SLAM框架
- ch02-02 SLAM问题的数学表述
- ch03 三维空间刚体运动
- ch03.01 旋转矩阵:点和向量,坐标系
- ch03.02 坐标系间的欧氏变换
- 01:欧式变换:
- 02:旋转矩阵RRR 的推导 :
- 03 旋转矩阵RRR 的性质
- 04 欧式变换的向量表示:
- ch03.03 变换矩阵与齐次坐标
- 01变换矩阵TTT:
- 02变换矩阵 T 的性质:
- ch03.04 齐次坐标(Homogeneous Coordinate)的优势
- 优势1:方便判断是否在直线或平面上
- 优势2:方便表示线线交点和点点共线
- 优势3:能够区分向量和点
- 优势4:能够表达无穷远点
- 优势5:能够简洁的表示变换
- ch03.05 旋转向量和欧拉角
- 01 旋转向量
- ch03.06 欧拉角
- ch03.07 四元数
- 01 四元数的定义
- 02 用单位四元数表示旋转
- ch04 李群与李代数
- ch04-01 李群与李代数基础
- 1. 群的定义
- 2. 李代数的定义
- 3. 李代数so(3)
- ch04-02 李群与李代数的转换关系:指数映射和对数映射
- 1. SO(3)和so(3)间的转换关系
- 2.SE(3)和se(3)间的转换关系
- 3. 从SE(3)到se(3)的对数映射可表示为:
- ch04-03 李代数求导: 引入李代数的一大动机就是方便求导优化
- 1. 群乘法与李代数加法的关系
- 2. *SO*(3)上的李代数求导
- 李代数求导
- 扰动模型(左乘)
- 3. *SE*(3)上的李代数求导
- ch05 相机与图像
- ch05-01 针孔相机模型
- ch05-02 畸变模型
- ch05-03 单目相机的成像过程
- ch06 非线性优化
- ch06-01 状态估计问题
- ch06-02 最小二乘
- 基于观测数据z z*z*的最小二乘
- ch06-03 非线性最小二乘
- 1. 一阶梯度法(一阶梯度又称最速下降法)和二阶梯度法(牛顿法)
- 2. 高斯牛顿法
- 3.列文伯格-马夸尔特方法
- ch07 视觉里程计01
- ch07 -01 特征点匹配
- ch07 -02 2D-2D匹配: 对极几何
- ch07 -03 3D-2D匹配: PnP(Perspective-n-Point)
- 1. 直接线性变换(DLT): 先求解相机位姿,再求解空间点位置**
- 2. P3P: 先求解空间点位置,再求解相机位姿
- 3. Bundle Adjustment: 最小化重投影误差,同时求解空间点位置和相机位姿
- 4.EPnP求解位姿
- ch07 -04 3D-3D匹配: ICP
- 1. SVD方法
- 2. 非线性优化方法
- 3. SVD方法求解
- 4. 非线性优化方法求解
ch02 初识SLAM
ch02-01 经典视觉SLAM框架
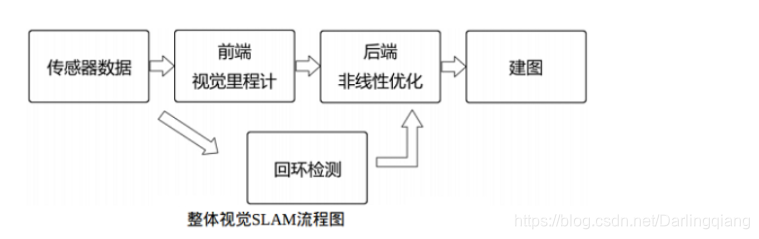
视觉SLAM流程包括以下步骤:
- 传感器信息读取: 在视觉SLAM中主要为相机图像信息的读取和预处理.如果是在机器人中,还可能有码盘、惯性传感器等信息的读取和同步.
- 视觉里程计(Visual Odometry,VO): 视觉里程计的任务是估算相邻图像间相机的运动,以及局部地图的样子.VO又称为前端(Front End).
视觉里程计不可避免地会出现累积漂移(Accumulating Drift)问题.
- 后端优化 (Optimization): 后端接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图.由于接在VO之后,又称为后端(Back End).
在视觉 SLAM中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法.
- 回环检测 (Loop Closing): 回环检测判断机器人是否到达过先前的位置.如果检测到回环,它会把信息提供给后端进行处理.
- 建图 (Mapping): 它根据估计的轨迹,建立与任务要求对应的地图.
地图的形式包括度量地图(精确表示地图物体的位置关系)与拓扑地图(更强调地图元素之间的关系)两种.
ch02-02 SLAM问题的数学表述
“小萝卜携带着传感器在环境中运动”,由如下两件事情描述:
- 1.什么是运动 ?我们要考虑从k − 1时刻到 k 时刻,小萝卜的位置 x 是如何变化的.
运动方程:
xk=f(xk−1,uk,wk)x_k = f(x_{k-1},u_k,w_k)xk=f(xk−1,uk,wk)
x_k, x_{k-1}表示小罗卜在k和k−1时刻的位置,表示小罗卜在k和 k-1 时刻的位置,表示小罗卜在k和k−1时刻的位置,u_k 表示运动传感器的读数(有时也叫输入) ,wkw_kwk 表示运动噪声
- 2.什么是观测 ?假设小萝卜在kkk时刻于 x_k处探测到了某一个路标y_j,我们要考虑这件事情是如何用数学语言来描述的.
观测方程:
zk,j=h(yj,xk,vk,j)z_{k,j} = h(y_{j},x_k,v_{k,j}) zk,j=h(yj,xk,vk,j)
zk,jz_{k,j}zk,j表示小萝卜在xkx_kxk位置上看到路标点 xkx_kxk,产生的观测数据; yjy_jyj表示第 j个路标点 ;vk,j)v_{k,j})vk,j)表示观测噪声
这两个方程描述了最基本的SLAM问题:当知道运动测量的读数u ,以及传感器的读数z 时,如何求解定位问题(估计x )和建图问题(估计 y).这时,我们就把SLAM问题建模成了一个状态估计问题:如何通过带有噪声的测量数据,估计内部的、隐藏着的状态变量?
ch03 三维空间刚体运动
ch03.01 旋转矩阵:点和向量,坐标系
01 向量a在线性空间的基[e1,e2,e3][e_1,e_2,e_3][e1,e2,e3]下的坐标为[a1,a2,a3]T[a_1,a_2,a_3]^T[a1,a2,a3]T.
a=[e1,e2,e3][a1a2a3]=a1e1+a2e2+a3e3a = [e_1,e_2,e_3] \left[ { a_1\\ a_2\\ a_3 } \right]=a_1e_1+a_2e_2+a_3e_3a=[e1,e2,e3][a1a2a3]=a1e1+a2e2+a3e3
02 向量的内积与外积
2.1 向量的内积: 描述向量间的投影关系
a⋅b=aTb=Σi−13a1bi=∣a∣∣b∣cos<a,b>a\cdot b = a^Tb= \displaystyle \Sigma^3_{i-1}a_1b_i=|a||b|cos<a,b> a⋅b=aTb=Σi−13a1bi=∣a∣∣b∣cos<a,b>
2.2 向量的外积: 描述向量的旋转
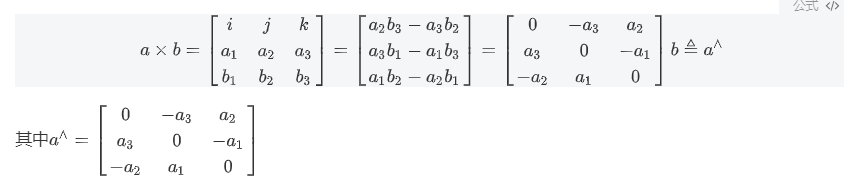
ch03.02 坐标系间的欧氏变换
01:欧式变换:
在欧式变换前后的两个坐标系下,同一个向量的模长和方向不发生改变,是为欧式变换. 一个欧式变换由一个旋转和一个平移组成.
02:旋转矩阵RRR 的推导 :
设单位正交基[e1,e2,e3][e_1,e_2,e_3][e1,e2,e3] 经过一次旋转变成了 [e1’,e2’,e3’][e^{’}_1,e^{’}_2,e^{’}_3][e1’,e2’,e3’] 对于同一个向量a,在两个坐标系下的坐标分别为[a1,a2,a3][a_1,a_2,a_3][a1,a2,a3]和 [a1,a2,a3]T[a_1,a_2,a_3]^T[a1,a2,a3]T. 根据坐标的定义:
[e1,e2,e3][a1a2a3]=[e1’,e2’,e3’][a1’a2’a3’][e_1,e_2,e_3]\left[\begin{matrix} a_1\\ a_2\\ a_3\end{matrix} \right] =[e^{’}_1,e^{’}_2,e^{’}_3]\left[\begin{matrix} a^{’}_1\\ a^{’}_2\\ a^{’}_3\end{matrix} \right ][e1,e2,e3]⎣⎡a1a2a3⎦⎤=[e1’,e2’,e3’]⎣⎡a1’a2’a3’⎦⎤
等式左右两边同时左乘[e1T,e2T,e3T][e^{T}_1,e^{T}_2,e^{T}_3][e1T,e2T,e3T], 得到
[a1a2a3]=[e1Te1’e1Te2’e1Te3’e2Te1’e2Te2’e2Te3’e3Te1’e3Te2’e3Te3’][a1’a2’a3’]≜Ra′\left[\begin{matrix} a_1\\ a_2\\ a_3\end{matrix} \right] = \left[\begin{matrix} e^{T}_1e^{’}_1 &e^{T}_1e^{’}_2 &e^{T}_1e^{’}_3 \\ e^{T}_2e^{’}_1 &e^{T}_2e^{’}_2 &e^{T}_2e^{’}_3\\ e^{T}_3e^{’}_1 &e^{T}_3e^{’}_2 &e^{T}_3e^{’}_3 \end{matrix} \right] \left[\begin{matrix} a^{’}_1\\ a^{’}_2\\ a^{’}_3 \end{matrix} \right] \triangleq Ra^{'} ⎣⎡a1a2a3⎦⎤=⎣⎡e1Te1’e2Te1’e3Te1’e1Te2’e2Te2’e3Te2’e1Te3’e2Te3’e3Te3’⎦⎤⎣⎡a1’a2’a3’⎦⎤≜Ra′
矩阵$ R$描述了旋转,称为旋转矩阵.
03 旋转矩阵RRR 的性质
旋转矩阵是**行列式为1的正交矩阵,**任何行列式为1的正交矩阵也是一个旋转矩阵.所有旋转矩阵构成特殊正交群SOSOSO:
SO(n)={R∈Rnxn∣RRT=I,det(R)=I}SO(n) = \{ R\in \mathbb{R}^{nxn}|RR^{T} = I, det(R) = I \} SO(n)={R∈Rnxn∣RRT=I,det(R)=I}
旋转矩阵是正交矩阵(其转置等于其逆),旋转矩阵的逆R−1R^{-1}R−1 (即转置RTR^{T}RT )描述了一个相反的旋转.
04 欧式变换的向量表示:
世界坐标系中的向量a,经过一次旋转(用旋转矩阵RRR描述)和一次平移(用平移向量ttt描述)后,得到了a’a^{’}a’
a’=Ra+ta^{’} = Ra+t a’=Ra+t
ch03.03 变换矩阵与齐次坐标
01变换矩阵TTT:
在三维向量的末尾添加1,构成的四维向量称为齐次坐标.将旋转和平移写入变换矩阵TTT中,得到:
[a’1]=[Rt01]≜T[a1]\left[\begin{matrix} a^{’} \\ 1\end{matrix} \right] = \left[\begin{matrix} R &t \\0 &1\end{matrix} \right] \triangleq T \left[\begin{matrix} a \\ 1\end{matrix} \right] [a’1]=[R0t1]≜T[a1]
齐次坐标的意义在于将欧式变换表示为线性关系**.
02变换矩阵 T 的性质:
变换矩阵TTT构成特殊欧式群SESESE
SE(3)={T=[Rt01]∈R4x4∣R∈SO(3),t∈R3}SE(3) =\{ T =\left[\begin{matrix} R &t \\0 &1\end{matrix} \right] \in \mathbb{R}^{4x4}|R\in \mathbb SO(3),t\in \mathbb{R}^{3}\} SE(3)={T=[R0t1]∈R4x4∣R∈SO(3),t∈R3}
变换矩阵的逆表示一个反向的欧式变换
T−1=[RT−RTt01]T^{-1} = \left[\begin{matrix} R^{T} &-R^{T}t \\0 &1\end{matrix} \right] T−1=[RT0−RTt1]
ch03.04 齐次坐标(Homogeneous Coordinate)的优势
优势1:方便判断是否在直线或平面上
若点p={x,y}p=\{ x,y\}p={x,y},在直线l=(a,b,c)l = (a,b,c)l=(a,b,c)上,则有:
ax+by+c=[a,b,c]T⋅[x,y,1]=lT⋅p’=0ax+by+c = [a,b,c]^{T}\cdot [x,y,1] = l^T \cdot p^{’} = 0 ax+by+c=[a,b,c]T⋅[x,y,1]=lT⋅p’=0
若点p={x,y,z}p=\{ x,y,z\}p={x,y,z},在平面A=(a,b,c,d)A = (a,b,c,d)A=(a,b,c,d)上,则有:
ax+by+cz+d=[a,b,c,d]T⋅[x,y,z,1]=AT⋅p’=0ax+by+cz+d = [a,b,c,d]^{T}\cdot [x,y,z,1] = A^T \cdot p^{’} = 0 ax+by+cz+d=[a,b,c,d]T⋅[x,y,z,1]=AT⋅p’=0
优势2:方便表示线线交点和点点共线
在齐次坐标下,
可以用两个点p,qp,qp,q的齐次坐标叉乘结果表示它们的共线l
可以用两条直线 l,ml,ml,m 的齐次坐标叉乘结果表示它们的交点 x
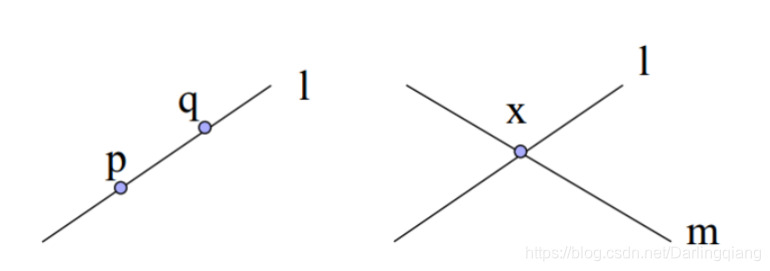
这里利用叉乘的性质: 叉乘结果与两个运算向量都垂直:
性质1的证明:
lT⋅p=(p×q)⋅p=0lT⋅q=(p×q)⋅q=0l^T \cdot p ={(p \times q) \cdot p}= 0 \\ l^T \cdot q ={(p \times q) \cdot q}= 0 lT⋅p=(p×q)⋅p=0lT⋅q=(p×q)⋅q=0
性质2的证明:
lT⋅p=lT⋅(l×m)=0mT⋅p=mT⋅(l×m)=0l^T \cdot p ={l^T \cdot(l \times m)}= 0 \\ m^T \cdot p ={m^T \cdot(l \times m)}= 0 lT⋅p=lT⋅(l×m)=0mT⋅p=mT⋅(l×m)=0
优势3:能够区分向量和点
点(x,y,z)(x,y,z)(x,y,z)的齐次坐标为(x,y,z,1)(x,y,z,1)(x,y,z,1)
向量(x,y,z)(x,y,z)(x,y,z)的齐次坐标为(x,y,z,0)(x,y,z,0)(x,y,z,0)
优势4:能够表达无穷远点
对于平行直线l=(a,b,c)l = (a,b,c)l=(a,b,c)和m=(a,b,d)m=(a,b,d)m=(a,b,d),求取其交点的齐次坐标x=l×m=(kb,−ka,0)x=l \times m =(kb,-ka,0)x=l×m=(kb,−ka,0),将其转为非齐次坐标,得到x=(kb/0,−ka/0)=(inf,−inf)x=(kb/0,-ka/0) = (inf,-inf)x=(kb/0,−ka/0)=(inf,−inf),这表示无穷远点.
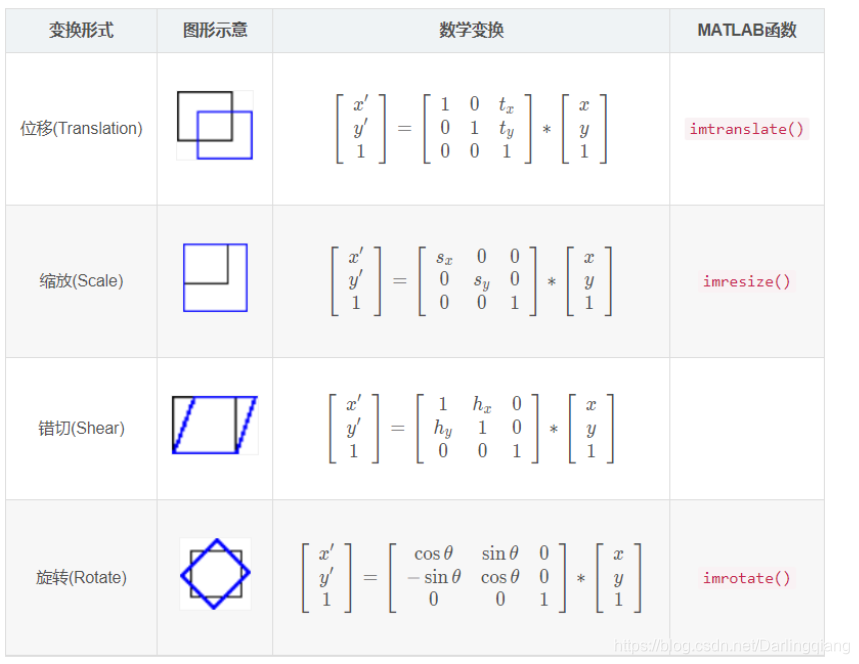
优势5:能够简洁的表示变换
使用齐次坐标,可以将加法运算转化为乘法运算.
ch03.05 旋转向量和欧拉角
01 旋转向量
旋转矩阵的缺点:
- 旋转矩阵有9个量,但一次旋转只有3个自由度,这种表达方式是冗余的.
- 旋转矩阵自带约束(必须是行列式为1的正交矩阵),这些约束会给估计和优化带来困难.
旋转向量: 任意旋转都可以用一个旋转轴和一个旋转角 来刻画.于是,我们可以使用一个向量,其方向表示旋转轴而长度表示旋转角.这种向量称为旋转向量(或轴角,Axis-Angle).
假设有一个旋转轴为$ n$,角度为 θ\thetaθ的旋转,其对应的旋转向量为 θn\theta nθn
旋转向量和旋转矩阵之间的转换:罗德里格斯公式
设旋转向量R表示一个绕单位向量n,角度为θ的旋转.
旋转向量到旋转矩阵:
R=cosθI+(1−cosθ)nnT+sinθn∧R = cos \theta I + (1-cos\theta)nn^{T} + sin\theta n^{\wedge} R=cosθI+(1−cosθ)nnT+sinθn∧
旋转矩阵到旋转向量:
旋转角 θ=arccos((tr(R)−1)/2)\theta =arccos((tr(R)- 1)/2)θ=arccos((tr(R)−1)/2)
旋转轴n是矩阵R RR特征值1对应的特征向量
ch03.06 欧拉角
欧拉角将一次旋转分解成3个分离的转角.常用的一种ZYX转角将任意旋转分解成以下3个轴上的转角:
绕物体的Z轴旋转,得到偏航角yaw
绕旋转之后的Y轴旋转,得到俯仰角pitch
绕旋转之后的X轴旋转,得到滚转角roll
- 欧拉角的一个重大缺点是万向锁问题(奇异性问题): 在俯仰角为$\pm$90° 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转).
ch03.07 四元数
为什么需要四元数: 对于三维旋转,找不到不带奇异性的三维向量描述方式.因此引入四元数.四元数是一种扩展的复数,既是紧凑的,也没有奇异性.
01 四元数的定义
1.四元数的定义
一个四元数q qq拥有一个实部和三个虚部
q=q0+q1i+q2j+q3kq = q_0 +q_1 i + q_2 j + q_3 kq=q0+q1i+q2j+q3k
其中i,j,ki,j,ki,j,k,为四元数的3个虚部,它们满足以下关系式(自己和自己的运算像复数,自己和别人的运算像叉乘):
i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j\begin{array}{rcl} i^2 =j^2 =k^2 = -1 \\ ij =k,ji=-k\\ jk=i,kj=-i \\ ki=j,ik=-j \end{array}i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j
也可以用一个标量和一个向量来表达四元数:
q=[s,v],s=q0∈R,v=[q1,q2,q3]T∈R3x3q = [s,v],s =q_0\in \mathbb{R} ,v = [q_1,q_2,q_3]^{T}\in \mathbb{R^{3x3}} q=[s,v],s=q0∈R,v=[q1,q2,q3]T∈R3x3
s为四元数的实部,v 为四元数的虚部.有实四元数和虚四元数的概念.
2.四元数与旋转角度的关系:
在二维情况下,任意一个旋转都可以用单位复数来描述,乘i ii就是绕i ii轴旋转90°.
在三维情况下,任意一个旋转都可以用单位四元数来描述,乘i ii就是绕i ii轴旋转180°.
3.单位四元数和旋转向量之间的转换:
设单位四元数q 表示一个绕单位向量$ n=[n_x,n_y,n_z]^T$,角度为 θ的旋转.
3.1 从旋转向量到单位四元数:
q=[cos(θ/2),nsin(θ/2)]T=[cos(θ2),nxsin(θ2),nysin(θ2),nzsin(θ2)]Tq =[cos(\theta/2),nsin(\theta/2)]^T = [cos(\frac{\theta}{2}),n_xsin(\frac{\theta}{2}),n_ysin(\frac{\theta}{2}),n_zsin(\frac{\theta}{2})]^T q=[cos(θ/2),nsin(θ/2)]T=[cos(2θ),nxsin(2θ),nysin(2θ),nzsin(2θ)]T
3.2 从单位四元数到旋转向量
{θ=2arccos(q0)[nx,ny,nz]=[q1,q2,q3]T/sin(θ2)\left\{ \begin{aligned} \theta & = 2arc\cos(q_0) \\ \left[n_x,n_y,n_z\right] & = [q_1,q_2,q_3]^T/sin(\frac{\theta}{2}) \\ \end{aligned} \right. ⎩⎨⎧θ[nx,ny,nz]=2arccos(q0)=[q1,q2,q3]T/sin(2θ)
02 用单位四元数表示旋转
给定一个空间三维点$p= [ x , y , z ] ∈ R3 ,p=[x,y,z ] R^3, p=[x,y,z]∈R ^3 $,以及一个由轴角n,θ指定的旋转,三维点p 经过旋转后变为p′.如何使用单位四元数q 表达旋转?
- 把三维空间点用一个虚四元数p 表示:
p=[0,x,y,z]=[0,v]p =[0,x,y,z] = [0,v] p=[0,x,y,z]=[0,v]
把旋转用单位四元数q qq表示:
q=[cos(θ2),nsin(θ2)q = [cos(\frac{\theta}{2}),nsin(\frac{\theta}{2}) q=[cos(2θ),nsin(2θ)旋转后的点 p′ 可表示为:
p’=qpq−1p^{’} = qpq^{-1} p’=qpq−1
这样得到的点p’ 仍为一个纯虚四元数,其虚部的3个分量表示旋转后3D点的坐标.
只有单位四元数才能表示旋转,因此在程序中创建四元数后,要记得调用normalize()以将其单位化
ch04 李群与李代数
ch04-01 李群与李代数基础
旋转矩阵构成特殊正交群SO(3),变换矩阵构成了特殊欧氏群 SE(3).
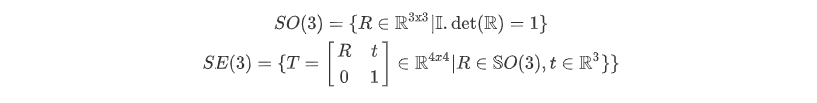
1. 群的定义
群(Group)是一种集合加上一种运算的代数结构.把集合记作A AA,运算记作⋅ \cdot⋅ ,那么群可以记作G = ( A , ⋅ ) G =(A,\cdot)G=(A,⋅).群要求这个运算满足如下条件(封结幺逆):
封闭性 $ ∀a_1,a_2∈A,a_1⋅a_2∈A. $
结合律 $ ∀ a_1,a_2,a_3∈A,(a_1⋅a_2)⋅a_3=a_1⋅(a_2⋅a_3) $
幺元 $ ∃ a_0∈A,s.t.∀ a∈A, a_0⋅a=a⋅a_0=a $
逆:$ ∀ a∈A,∃ a^{−1}∈ A ,s.t.a⋅a{−1}=a{0}$
李群是指具有连续(光滑)性质的群SO(3)和SE(3)都是李群
2. 李代数的定义
每个李群都有与之对应的李代数,李代数描述了李群的局部性质.
通用的李代数的定义如下:
李代数由一个集合V,一个数域 F 和一个二元运算[ , ] 组成.如果它们满足以下几条性质,则称(V,F,[,])(V, F, [, ])(V,F,[,])为一个李代数,记作$ g $.
封闭性: $ ∀ X,Y∈V,[X,Y]∈V. $
双线性: $ \forall X,Y,Z \in V, a,b \in F $
[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y][aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y] [aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y]自反性: $ ∀X,∈V,[X,X]=0. $
雅可比等价$ ∀ X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0 .其中的二元运算. 其中的二元运算.其中的二元运算[ , ]$ [,][,]被称为李括号.例如三维向量空间R3\mathbb{R^3}R3 上定义的叉积× \times×是一种李括号.
3. 李代数so(3)
3.1 李群SO(3)对应的李代数so(3)是定义在$ \mathbb{R^3}$ 上的向量,记作ϕ\phiϕ.
so(3)={ϕ∈R3,Φ=ϕ∧=a∧=[0−ϕ3ϕ2ϕ30−ϕ1−ϕ2ϕ10]∈R3x3}so(3)=\{ \phi \in \mathbb R^{3},\Phi=\phi^∧ = {a}^∧ =\left[\begin{matrix} &0 & -\phi_3 &\phi_2 \\ &\phi_3 &0 &-\phi_1 \\ &-\phi_2 & \phi_1 &0\end{matrix} \right] \in \mathbb R^{3x3} \}so(3)={ϕ∈R3,Φ=ϕ∧=a∧=⎣⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎤∈R3x3}
3.2 李代数so(3)的李括号为
[ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨[\phi_1,\phi_2] = (\Phi_1\Phi_2-\Phi_2\Phi_1)^∨ [ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨
其中 ∨ 是 ^ 的逆运算,表示将反对称矩阵还原为向量
3.3 so(3)和SO(3)间的映射关系为
- 李群R=exp(ϕ∧)=exp(Φ)R=exp(ϕ^∧)=exp(Φ)R=exp(ϕ∧)=exp(Φ)
- 李代数ϕ=ln(R)∨ϕ=ln(R)^∨ϕ=ln(R)∨
3.4 李代数se(3)
类似地,李群SE(3)的李代数se(3)是定义在 R6\mathbb{R^6}R6上上的向量.记作ξ\xiξ:
se(3)={ξ=[ρ,ϕ]∈R6,ρ∈R3,ξ∧=[0−ϕ3ϕ2ϕ30−ϕ1−ϕ2ϕ10]∈R4x4}se(3)=\{ \xi =\left[{\rho \\, \phi } \right] \in \mathbb R^6,\rho \in \mathbb R^3,\xi ^∧ =\left[\begin{matrix} &0 & -\phi_3 &\phi_2 \\ &\phi_3 &0 &-\phi_1 \\ &-\phi_2 & \phi_1 &0\end{matrix} \right] \in \mathbb R^{4x4} \}se(3)={ξ=[ρ,ϕ]∈R6,ρ∈R3,ξ∧=⎣⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎤∈R4x4}
se(3)中的每个元素ξ\xiξ,是一个六维向量.前三维ρ\rhoρ表示平移;后三维ϕ\phiϕ表示旋转,本质上是so(3)元素.
在这里同样使用^符号将六维向量扩展成为四维矩阵,但不再表示反对称
KaTeX parse error: Expected '}', got '&' at position 41: …atrix}{\phi^ ∧ &̲\rho \\ 0^T ,& …
李代数se(3)的李括号和so(3)类似:
[ξ1,ξ2]=(ξ1∧ξ2∧−ξ2∧ξ1∧)∨[\xi_1,\xi_2] = (\xi_1^{∧}\xi_2^{∧}-\xi_2^{∧}\xi_1^{∧})^∨ [ξ1,ξ2]=(ξ1∧ξ2∧−ξ2∧ξ1∧)∨
se(3)和SE(3)间映射关系为
李群 $ T=exp(ξ∧) $
李代数 $\xi = ln(T) ^{∨} $
ch04-02 李群与李代数的转换关系:指数映射和对数映射
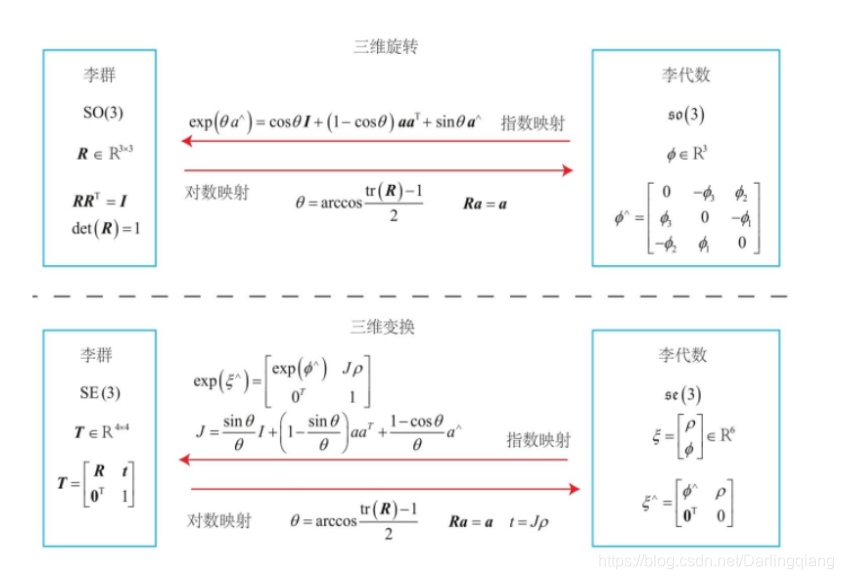
1. SO(3)和so(3)间的转换关系
将三维向量ϕ 分解为其模长θ和方向向量$ \alpha$,即ϕ = θ α .则从so(3)到SO(3)的指数映射可表示为:
R=exp(ϕ)=exp(θα∧)=cosθI+(1−cosθ)ααT+sinθα∧R=exp(ϕ)=exp(θα ∧ )=cosθI+(1−cosθ)αα T +sinθα ∧ R=exp(ϕ)=exp(θα∧)=cosθI+(1−cosθ)ααT+sinθα∧
上式即为旋转向量到旋转矩阵的罗德里格斯公式,可见so(3)本质上是旋转向量组成的空间.
从SO(3)到so(3)的对数映射可表示为:
ϕ=ln(R)V\phi = ln(R)^{V} ϕ=ln(R)V
实际计算时可以通过迹的性质分别求出转角θ和转轴α
θ=arccostr(R)−12,Rα=αθ=arccos \frac{tr(R)−1}{2},Rα=α θ=arccos2tr(R)−1,Rα=α
2.SE(3)和se(3)间的转换关系
从se(3)到SE(3)的指数映射可表示为:
T=exp(ξ∧)=[RJρ0T,1]T =exp(\xi ^{∧}) =\left[ \begin{matrix} R&J\rho \\ 0^T ,& 1 \end{matrix} \right]T=exp(ξ∧)=[R0T,Jρ1]
J=sinθthetaI+(1−sinθθααT)+(1−cosθθα∧)J =\frac{sin\theta}{theta}I + (1 - \frac{sin\theta}{\theta}\alpha\alpha^{T}) + (1 - \frac{cos\theta}{\theta}\alpha^{∧}) J=thetasinθI+(1−θsinθααT)+(1−θcosθα∧)
可以看到,平移部分经过指数映射之后,发生了一次以J 为系数矩阵的线性变换.
3. 从SE(3)到se(3)的对数映射可表示为:
ξ=ln(T)∨\xi =ln(T)^{∨} ξ=ln(T)∨
实际计算时ϕ 可以由SO(3)到so(3)的映射得到,ρ 可以由t = J ρ计算得到.
ch04-03 李代数求导: 引入李代数的一大动机就是方便求导优化
1. 群乘法与李代数加法的关系
BCH公式及其近似形式
很遗憾地,李群乘积和李代数加法并不等价,即:
R1R2=exp(ϕ1∧)exp(ϕ2∧)≠exp((ϕ1+ϕ2)∧)R_1R_2 =exp(\phi_1^{∧})exp(\phi_2^{∧})\neq exp((ϕ 1 +ϕ 2 ) ∧ ) R1R2=exp(ϕ1∧)exp(ϕ2∧)=exp((ϕ1+ϕ2)∧)
李群乘积与李代数运算的对应关系由BCH公式给出:
ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+...ln(exp(A)exp(B))=A+B+ 2 1 [A,B]+ 12 1 [A,[A,B]]− 12 1 [B,[A,B]]+... ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+...
上式中[ , ] [,][,]表示李括号运算.当ϕ1\phi_1ϕ1 或ϕ 2 为小量时,可以对BCH公式进行线性近似,得到李群乘积对应的李代数的表达式:
R1⋅R2对应的李代数
=ln(exp(ϕ1∧)exp(ϕ1∧))∨≈Jl(ϕ2)−1ϕ1+ϕ2(ifϕ1−>min)≈Jl(ϕ1)−1ϕ2+ϕ1(ifϕ2−>min)=ln(exp(ϕ_1^{∧})exp(ϕ_1^{∧}))^{∨} \\\approx {J_l(\phi_2)^{−1}\phi_1+ϕ_2}( if \phi_1->min) \\\approx {J_l(\phi_1)^{−1}\phi_2+ϕ_1}( if \phi_2->min) =ln(exp(ϕ1∧)exp(ϕ1∧))∨≈Jl(ϕ2)−1ϕ1+ϕ2(ifϕ1−>min)≈Jl(ϕ1)−1ϕ2+ϕ1(ifϕ2−>min)
$$
其中左乘雅可比矩阵JlJ_lJl,即为从SE(3)到se(3)对数映射中的雅可比矩阵
Jl=sinθθI+(1−sinθθααT+1−cosθθα∧)J_l = \frac{sin\theta}{\theta}I + (1- \frac{sin\theta}{\theta} \alpha \alpha^{T} +\frac{1-cos\theta}{\theta}\alpha^{∧}) Jl=θsinθI+(1−θsinθααT+θ1−cosθα∧)
其逆为
Jl−1=θ2cotθ2I+(I−θ2cotθ2)ααT+θ2α∧J_l^{-1} = \frac{\theta}{2}cot\frac{\theta}{2}I+(I-\frac{\theta}{2}cot\frac{\theta}{2})\alpha \alpha^{T} + \frac{\theta}{2}\alpha^{∧} Jl−1=2θcot2θI+(I−2θcot2θ)ααT+2θα∧
右乘雅可比矩阵只需对自变量取负号即可
Jr(ϕ)=Jr(−ϕ)J_r(\phi) = J_r(-\phi) Jr(ϕ)=Jr(−ϕ)
3. 李群SO(3)乘法与李代数so(3)加法的关系:
对旋转R (李代数为ϕ)左乘一个微小旋转ΔR(李代数为Δϕ),得到的旋转李群ΔR⋅R对应的李代数为:
=ln(exp(Δϕ∧)exp(Δϕ∧))=ϕ+Jl−1(ϕ)Δϕ=ln(exp(\Delta\phi^{∧})exp(\Delta\phi^{∧})) = \phi+J_l^{-1}(\phi)\Delta \phi =ln(exp(Δϕ∧)exp(Δϕ∧))=ϕ+Jl−1(ϕ)Δϕ
反之,李代数加法(ϕ+Δϕ)对应的李群元素可表示为:
exp((ϕ+Δϕ)∧))=exp((JlΔϕ)∧)exp(ϕ)∧))=exp(ϕ)∧exp((JrΔϕ)∧)exp((\phi+\Delta\phi)^{∧})) =exp(( J_l\Delta \phi)^{∧})exp( \phi)^{∧})) = exp(\ \phi)^{∧}exp((J_r\Delta\phi)^{∧}) exp((ϕ+Δϕ)∧))=exp((JlΔϕ)∧)exp(ϕ)∧))=exp( ϕ)∧exp((JrΔϕ)∧)
4. 同理,李群SE(3)乘法与李代数se(3)加法的关系:
5.
exp(Δξ∧)exp(ξ∧)≈exp((Jl−1Δξ+ξ)∧)exp(ξ∧)exp(Δξ∧)≈exp((Jr−1Δξ+ξ)∧)exp(\Delta \xi^{∧})exp( \xi^{∧}) \approx exp((J_l^{-1}\Delta \xi+\xi)^{∧}) \\ exp( \xi^{∧}) exp(\Delta \xi^{∧})\approx exp((J_r^{-1}\Delta \xi+\xi)^{∧}) exp(Δξ∧)exp(ξ∧)≈exp((Jl−1Δξ+ξ)∧)exp(ξ∧)exp(Δξ∧)≈exp((Jr−1Δξ+ξ)∧)
2. SO(3)上的李代数求导
对空间点p进行旋转,得到Rp,旋转之后点的坐标对旋转的导数可表示为:
φ(Rp)φ(R)\frac{\varphi(Rp)}{\varphi(R)} φ(R)φ(Rp)
对于上式的求导,有两种方式:
1.用李代数ϕ表示姿态R,然后根据李代数加法对ϕ 求导.
2.用李代数φ 表示微小扰动∂ R ,然后根据李群左乘对φ 求导.
其中扰动模型表达式简单,更为实用.
李代数求导
用李代数ϕ 表示姿态R,求导得到
φ(Rp)φ(R)=φ(exp(ϕ)∧pφ(ϕ)\frac{\varphi(Rp)}{\varphi(R)} =\frac{\varphi(exp(\phi)^{∧ }p}{\varphi(\phi)} φ(R)φ(Rp)=φ(ϕ)φ(exp(ϕ)∧p
扰动模型(左乘)
另一种求导方式是对R进行一次左乘扰动∂R,设左乘扰动∂R对应的李代数为φ,对φ求导,得到
φ(Rp)φ(R)=exp((ϕ+φ)∧)p−exp(ϕ∧)pφ=−(Rp)∧\frac{\varphi(Rp)}{\varphi(R)} =\frac{exp((\phi+\varphi)^{∧})p-exp(\phi^{∧})p}{\varphi} = -(Rp)^{∧} φ(R)φ(Rp)=φexp((ϕ+φ)∧)p−exp(ϕ∧)p=−(Rp)∧
3. SE(3)上的李代数求导
类似地,空间点p经过变换T得到Tp,给T左乘一个扰动ΔT=exp(δξ∧)\Delta T =exp(\delta \xi^{ ∧ })ΔT=exp(δξ∧),则有
KaTeX parse error: Undefined control sequence: \matrix at position 43: …(\xi)} =\left[ \̲m̲a̲t̲r̲i̲x̲{I&-(Rp+t)^{∧} …
ch05 相机与图像
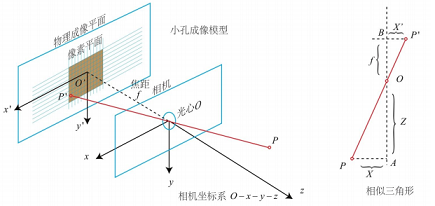
ch05-01 针孔相机模型
O−x−y−z为相机坐标系,现实空间点 P 的相机坐标为$[X,Y,Z]^T ,投影到O′−x′−y′平面上的点P′,坐标为,投影到O ′ − x ′ − y ′ 平面上的点P' ,坐标为,投影到O′−x′−y′平面上的点P′,坐标为[X’,Y’,Z’]^T$.
将成像平面对称到相机前方,根据几何相似关系Zf=XX′=YY′\frac{Z}{f}=\frac{X}{X^{'}}=\frac{Y}{Y^{'}}fZ=X′X=Y′Y ,整理得到投影点P ′ 在投影平面上的坐标P′=[X′,Y′]P'=[X',Y']P′=[X′,Y′]
{X′=fXZY′=fYZ\left\{ \begin{aligned} X^{'}=f \frac{X}{Z} \\ Y^{'}=f \frac{Y}{Z} \\ \end{aligned} \right. ⎩⎪⎪⎨⎪⎪⎧X′=fZXY′=fZY
转换得到投影点P ′ 在像素平面上的像素坐标Pu,v=[u,v]TP_{u,v} = [u, v]^TPu,v=[u,v]T
{u=αX′+cx=fxXZ+cxv=βY′+cy=fyYZ+cy\left\{ \begin{aligned} u=\alpha X^{'}+c_{x}=f_x \frac{X}{Z}+c_{x} \\ v=\beta Y^{'}+c_{y}=f_y \frac{Y}{Z} +c_{y}\\ \end{aligned} \right. ⎩⎪⎪⎨⎪⎪⎧u=αX′+cx=fxZX+cxv=βY′+cy=fyZY+cy
其中,u,v,cx,cy,fx,fyu,v,c_x,c_y,f_x,f_yu,v,cx,cy,fx,fy的单位为像素,α,β\alpha, \betaα,β的单位为像素/米.
将上式写成矩阵形式,得到**现实空间点相机坐标P和投影点像素坐标Puv∗∗P_{uv}**Puv∗∗之间的关系:
ZPuv=[uv1][x0cx0fycy001]≜KPZP_{uv} = \left[ \begin{matrix} u\\ v \\1 \end{matrix} \right] \left[ \begin{matrix} _x & 0 &c_x\\0& f_y &c_y \\0 &0 &1 \end{matrix} \right]\triangleq KPZPuv=⎣⎡uv1⎦⎤⎣⎡x000fy0cxcy1⎦⎤≜KP
其中矩阵K称为相机的内参数矩阵.
上式中的P 为现实空间点在相机坐标系下的相机坐标,将其转为世界坐标pwp_wpw,有
ZPuv=K(RPw+t)=KTPwZP_{uv}=K(RP_{w}+t) =KTP_{w} ZPuv=K(RPw+t)=KTPw
因此R ,t (或T )又称为相机的外参数.
将最后一维进行归一化处理,得到点P PP在归一化平面的归一化坐标 $P c = [ X / Z , Y / Z , 1 ] ^T $
Pc=PZ=K−1PuvP_c =\frac{P}{Z}=K^{-1}P_{uv} Pc=ZP=K−1Puv
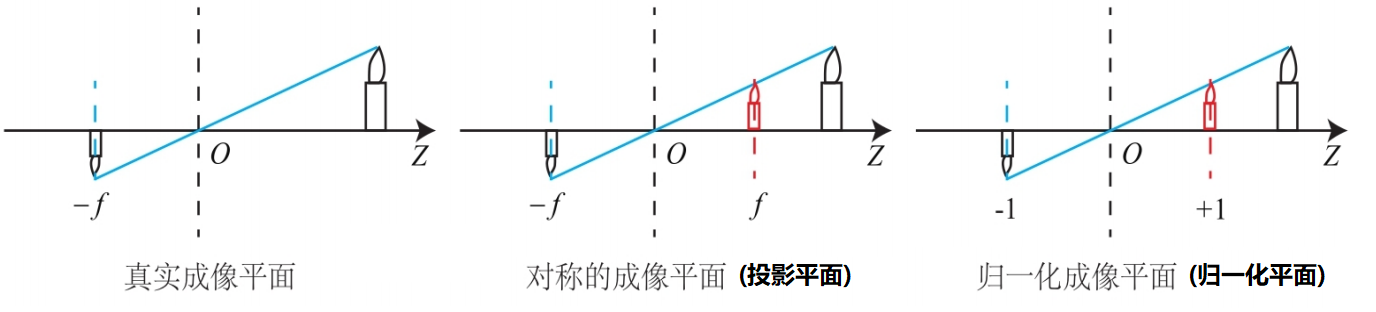
参数矩阵有内参数K和外参数R,t,其中:
内参数矩阵K体现了归一化相机坐标到像素坐标的变换.
之所以是归一化坐标,这体现了投影性质:在某一条直线上的空间点,最终会投影到同一像素点上.
外参数矩阵R ,t (或T)体现了世界坐标到相机坐标的变换.
ch05-02 畸变模型
畸变包含两种: 径向畸变和切向畸变.
径向畸变: 由透镜形状引起,主要包括桶形畸变和枕形畸变.
可以看成坐标点沿着长度方向发生了变化,也就是其距离原点的长度发生了变化.
xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)x_{distorted} =x(1+k_1 r^2 +k_2 r^ 4 + k_3 r^6)\\ y_{distorted} =y(1+k_1 r^2 +k_2 r^ 4 + k_3 r^6) xdistorted=x(1+k1r2+k2r4+k3r6)ydistorted=y(1+k1r2+k2r4+k3r6)
切向畸变: 由透镜和成像平面不严格平行引起.可以看成坐标点沿着切线方向发生了变化,也就是水平夹角发生了变化.
xdistorted=x+2p1xy+p2(r2+2x2)ydistorted=y+p1(r2+2y2)+2p2xyx_{distorted} =x + 2p_1 xy+p_2(r^2 +2x^2)\\ y_{distorted} =y + p_1(r^2 +2y^2) +2p_2 xy xdistorted=x+2p1xy+p2(r2+2x2)ydistorted=y+p1(r2+2y2)+2p2xy
ch05-03 单目相机的成像过程
单目相机的成像过程:
- 世界坐标系下有一个固定的原点P,其世界坐标PwP_wPw
- 由于相机在运动,它的运动由R ,t 或变换矩阵T∈SE(3)T\in SE(3)T∈SE(3)描述.原点P的相机坐标Pc′=RPw+tP_c^{'}=RP_w +tPc′=RPw+t
- 这时Pc′P_c^{'}Pc′的分量为X,Y ,Z ,把它们投影到归一化平面Z =1上,得到P 的归一化相机坐标Pc′Z=[XZ,YZ,1]\frac{P_c^{'}}{Z}=[\frac{X}{Z} ,\frac{Y}{Z},1]ZPc′=[ZX,ZY,1]
- 有畸变时,根据畸变参数计算PcP_cPc发生畸变后的归一化相机坐标
- P的归一化相机坐标经过内参K后,对应到它的像素坐标Puv=KPcP_{u v }= K P_cPuv=KPc
在讨论相机成像模型时,我们一共谈到了四种坐标: 世界坐标、相机坐标、归一化相机坐标和像素坐标.请读者厘清它们的关系,它反映了整个成像的过程.
ch06 非线性优化
ch06-01 状态估计问题
最大后验与最大似然
SLAM模型由状态方程和运动方程构成:
{xk=f(xk−1,uk,wk)zk,j=h(yj,xk,vk,j)\left\{ \begin{aligned} x_{k} =f(x_{k-1},u_k,w_k) \\ z_{k,j} =h(y_j,x_k,v_{k,j})\\ \end{aligned} \right. {xk=f(xk−1,uk,wk)zk,j=h(yj,xk,vk,j)
通常假设两个噪声项wk,vk,jw_k , v_{k,j}wk,vk,j满足零均值的高斯分布:
wk∼N(0,Rk),vk,j∼N(0,Qk,j)w_k \sim N(0,R_k),v_{k,j}\sim N(0,Q_{k,j}) wk∼N(0,Rk),vk,j∼N(0,Qk,j)
对机器人的估计,本质上就是已知输入数据u 和观测数据z 的条件下,求机器人位姿x 和路标点y 的条件概率分布:
P(x,y∣z,u)P(x,y|z,u) P(x,y∣z,u)
利用贝叶斯法则,有:
P(x,y∣z,u)=P(z,u∣x,y)P(z,u)∝P(z,u∣x,y)P(x,y)P(x,y|z,u) = \frac{P(z,u|x,y)}{P(z,u)} \propto {P(z,u|x,y)}{P(x,y)} P(x,y∣z,u)=P(z,u)P(z,u∣x,y)∝P(z,u∣x,y)P(x,y)
其中,$P(x,y|z,u) $ 为后验概率 P(z,u∣x,y){P(z,u|x,y)}P(z,u∣x,y)为似然P(x,y)P(x,y)P(x,y)为先验,上式可表述为后验概 率 ∝ 似 然 ⋅ 先 验 后 直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下后验概率最大化则是可行的:
(x,y)MLE∗=argmaxP(x,y∣z,u)(x,y) ^∗_{MLE}=argmaxP(x,y∣z,u) (x,y)MLE∗=argmaxP(x,y∣z,u)
最大似然估计的直观意义为:在什么样的状态下,最可能产生现在观测到的数据.
ch06-02 最小二乘
基于观测数据z zz的最小二乘
对于某一次观测
zk,j=h(yj,xk)+vk,jz_{k,j}=h(y_j,x_k)+v_{k,j} zk,j=h(yj,xk)+vk,j
由于假设噪声$v k , j ∼ N ( 0 , Q k , j ) 则观测数据则观测数据则观测数据z_{j,k}$的似然为
P(zj,k∣xk,yJ)=N(h(yj,xk),Qk,j)P(z_{j,k}|x_k,y_J) =N(h(y_j,x_k),Q_{k,j}) P(zj,k∣xk,yJ)=N(h(yj,xk),Qk,j)
将上式代入高斯分布表达式中,并取负对数,得到
(xk,yj)∗=argmaxN(h(yj,xk),Qk,j)=argmin(zk,j−h(xk,yj))TQk,j−1(zk,j−h(xk,yj))(x_k,y_j) ^∗=argmaxN(h(y_j,x_k),Q_{k,j})\\ =arg min(z_{k,j}-h(x_k,y_j))^{T}Q^{-1}_{k,j}(z_{k,j}-h(x_k,y_j)) (xk,yj)∗=argmaxN(h(yj,xk),Qk,j)=argmin(zk,j−h(xk,yj))TQk,j−1(zk,j−h(xk,yj))
上式等价于最小化噪声项(即误差)的一个二次型,其中Qk,j−1Q^{-1}_{k,j}Qk,j−1称为信息矩阵,即高斯分布协方差矩阵的逆.
基于观测数据z 和输入数据u 的最小二乘
因为观测z 和输入u 是独立的,因此可对z 和u 的联合似然进行因式分解:
P(x,y∣z,u)=∏kP(uk∣xk−1,xk)∏P(zj,k∣xk,yj)P(x,y|z,u) =\prod_{k}P(u_k|x_{k-1},x_k) \prod P(z_{j,k}|x_k,y_j) P(x,y∣z,u)=k∏P(uk∣xk−1,xk)∏P(zj,k∣xk,yj)
定义输入和观测数据与模型之间的误差:
eu,k=xk−f(xk−1,uk)ez,j,k=zk,j−h(xk,yj)e_{u,k} =x_k -f(x_{k-1},u_k)\\ e_{z,j,k}=z_{k,j} -h(x_k,y_j) eu,k=xk−f(xk−1,uk)ez,j,k=zk,j−h(xk,yj)
定义
J(x,y)=∑keu,kTRk−1eu,k+∑k∑jek,jTQk,j−1ez,k,jJ(x,y)=\sum_k e^{T}_{u,k}R^{-1}_{k}e_{u,k}+\sum_{k}\sum_{j}e^{T}_{k,j}Q^{-1}_{k,j}e_{z,k,j} J(x,y)=k∑eu,kTRk−1eu,k+k∑j∑ek,jTQk,j−1ez,k,j
则有
(xk,yj)∗=argminJ(x,y)(x_k,y_j) ^∗=argmin J(x,y) (xk,yj)∗=argminJ(x,y)
ch06-03 非线性最小二乘
对于非线性最小二乘问题:
minxF(x)=12∣∣f(x)∣∣22min_xF(x) =\frac{1}{2}||f(x)||_2^{2} minxF(x)=21∣∣f(x)∣∣22
求解该问题的具体步骤如下:
- 给定某个初始值x0x_0x0
- 对于第k次迭代,寻找一个增量Δxk\Delta x_kΔxk,使得F(xk+Δxk)F(x_k +\Delta x_k)F(xk+Δxk)达到极小值
- 若Δxk\Delta x_kΔxk足够小,则停止
- 否则 ,令xk+1=xk+Δxkx_{k +1} =x_k +\Delta x_kxk+1=xk+Δxk,返回第2步xk+1=xk+Δxkx_{k+1}=x_k+Δx_kxk+1=xk+Δxk,返回第2步
这样,最小二乘问题被转化为一个不断寻找下降增量Δxk\Delta x_kΔxk的问题.,具体有以下方法
常见方法有 最速下降法,牛顿法,高斯牛顿法,LM法
1. 一阶梯度法(一阶梯度又称最速下降法)和二阶梯度法(牛顿法)
目标函数F(x)F(x)F(x)在xkx_kxk附近的Tayor展开
F(x+Δxk)≈F(xk)+J(xk)TΔxk+12ΔxkTH(xk)xkF(x+\Delta x_k) \thickapprox F(x_k)+J(x_k)^{T}\Delta x_k +\frac{1}{2} \Delta x_k^{T}H(x_k)x_k F(x+Δxk)≈F(xk)+J(xk)TΔxk+21ΔxkTH(xk)xk
其中J(x)J(x)J(x)是F(x)关于x的一阶导数矩阵,H(x)是F(x)关于x 的二阶导数矩阵.
其中若Δxk\Delta x_kΔxk 取一阶导数,则
Δxk∗=−J(xk)\Delta x_k ^{*} =-J(x_k) Δxk∗=−J(xk)
其中若Δxk\Delta x_kΔxk 取2阶导数,则
Δxk∗=argmin(F(xk)+J(xk)TΔxk+12ΔxkTH(xk)xk)\Delta x_k ^{*} =arg min(F(x_k)+J(x_k)^{T}\Delta x_k +\frac{1}{2} \Delta x_k^{T}H(x_k)x_k) Δxk∗=argmin(F(xk)+J(xk)TΔxk+21ΔxkTH(xk)xk)
令上市对Δxk\Delta x_kΔxk 导数为0,则求得
HΔxk=−JH \Delta x_k =-J HΔxk=−J
2. 高斯牛顿法
将f(x)f(x)f(x)在XkX_kXk附近进行泰勒展开 得
f(xk+Δxk)≈f(xk)+J(xk)Δxkf(x_k +\Delta x_k)\thickapprox f(x_k) + J(x_k)\Delta x_k f(xk+Δxk)≈f(xk)+J(xk)Δxk
则
Δxk∗=argminΔxk12∣∣f(xk)+J(xk)TΔxk∣∣2\Delta x_k ^{*} =arg min_\Delta x_k\frac{1}{2}||f(x_k) + J(x_k)^{T}\Delta x_k||^{2} Δxk∗=argminΔxk21∣∣f(xk)+J(xk)TΔxk∣∣2
令上式对Δx\Delta xΔx的导数为0,得到高斯牛顿方程
J(xk)f(xk)+J(xk)J(xk)TΔxk=0J(x_k)f(x_k) +J(x_k)J(x_k)^{T}\Delta x_k=0 J(xk)f(xk)+J(xk)J(xk)TΔxk=0
令 H(x)=J(xk)J(xk)T,g(x)=−J(x)f(x)H(x)=J(x_k)J(x_k)^{T},g(x)=-J(x)f(x)H(x)=J(xk)J(xk)T,g(x)=−J(x)f(x),则Δxk∗\Delta x_k ^{*}Δxk∗ 可以取 HΔxk=gH \Delta x_k =gHΔxk=g 的解 .
3.列文伯格-马夸尔特方法
泰勒展开只能在展开点附近才有较好的近似效果,因此应给Δx\Delta xΔx添加一个范围,称为信赖区域.
定义一个指标ρ\rhoρ刻画这个近似的好坏程度,其分子为实际函数下降的值,分母是近似模型下降的值:
ρ=f(x+Δx)−f(x)J(x)TΔx\rho =\frac{f(x+\Delta x)-f(x)}{J(x)^{T} \Delta x} ρ=J(x)TΔxf(x+Δx)−f(x)
通过调整ρ\rhoρ来确定信赖区域:
若ρ\rhoρ接近1,则近似是最好的.
若ρ\rhoρ太小,说明实际下降的值远小于近似下降的值,则认为近似比较差,需要缩小近似范围.
若ρ\rhoρ太大,说明实际下降的比预计的更大,我们可以放大近似范围.
列文伯格-马夸尔特方法算法步骤如下:
step 1:给定初始值x0x_0x0 ,以及初始优化半径μ\muμ
step 2:对于第k 次迭代,求解:
minΔxk12∣∣f(xk)+J(xk)TΔxk∣∣2s.t.∣∣DΔxk∣∣2≤μmin_{Δx_k} \frac{1}{2}||f(x_k) + J(x_k)^{T}\Delta x_k||^{2} \\ \quad \text{s.t.} ||D\Delta x_k||^2 \leq \mu minΔxk21∣∣f(xk)+J(xk)TΔxk∣∣2s.t.∣∣DΔxk∣∣2≤μ
其中,μ\muμ是信赖区域的半径,D 为系数矩阵step 3: 计算ρ
step 4: ρ>34\rho > \frac{3}{4}ρ>43 ,则μ=2μ\mu =2\muμ=2μ
step 5:ρ<14\rho < \frac{1}{4}ρ<41 ,则μ=0.5μ\mu =0.5\muμ=0.5μ
step 6: 若ρ大于某阈值,则认为近似可行.令 xk+1=xk+Δxkx_{k+1}=x_k +\Delta x_kxk+1=xk+Δxk
step 7:判断算法是否收敛.如不收敛则返回第2步,否则结束.
在step 2步中Δxk\Delta x_kΔxk的求解要使用拉格朗日乘数法:
L(Δxk,λ)=12∣∣f(xk)+J(xk)TΔxk∣∣2+λ2(∣∣DΔxk∣∣2−μ)L(\Delta x_k,\lambda) = \frac{1}{2}||f(x_k) + J(x_k)^{T}\Delta x_k||^{2}+\frac{\lambda}{2}(||D \Delta x_k||^2 -\mu) L(Δxk,λ)=21∣∣f(xk)+J(xk)TΔxk∣∣2+2λ(∣∣DΔxk∣∣2−μ)
令上式对Δxk\Delta x_kΔxk导数为0,得到
(H+λDTD)Δxk=g(H+\lambda D^TD )\Delta x_k =g (H+λDTD)Δxk=g
考虑简化形式,即D=I,则相当于求解
(H+λI)Δxk=g(H+\lambda I )\Delta x_k =g (H+λI)Δxk=g
当λ较小时,H占主要地位,这说明二次近似模型在该范围内是比较好的,列文伯格-马夸尔特方法更接近于高斯牛顿法.
当λ 比较大时,λI\lambda IλI占据主要地位,这说明二次近似模型在该范围内不够好,列文伯格-马夸尔特方法更接近于一阶梯度下降法.
ch07 视觉里程计01
ch07 -01 特征点匹配
特征点:根据特征点匹配计算相机运动
根据特征点匹配计算相机运动.根据相机的成像原理不同,分为以下3种情况:
- 当相机为单目时,我们只知道匹配点的像素坐标,是为2D-2D匹配,使用对极几何求解.以及弹幕初始化的过程。
- 当相机为双目或RGB-D时,我们就知道匹配点的像素坐标和深度坐标,是为3D-3D匹配,使用ICP求解.
- 如果有3D点及其在相机的投影位置,也能估计相机的运动,是为3D-2D匹配,使用PnP求解.
ch07 -02 2D-2D匹配: 对极几何
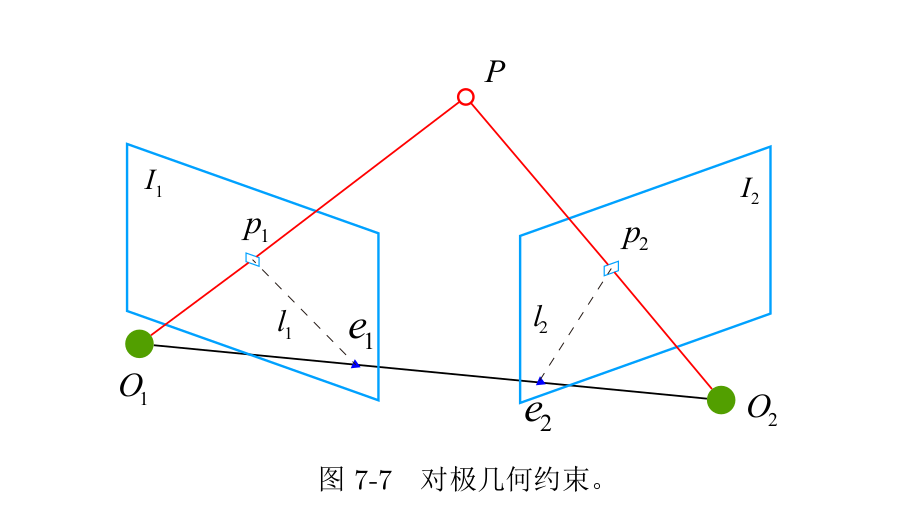
考虑从两张图像上观测到了同一个3D点,如图所示**。**我们希望可以求解相机两个时刻的运动R,tR,tR,t。
假设我们要求取两帧图像I1,I2I_1,I_2I1,I2之间的运动,设第一帧到第二帧的运动为R ,t,两个相机中心分别为O1,O2O_1,O_2O1,O2.考虑I1I_1I1中有一个特征点p1p_1p1,它在I2I_2I2中对应着特征点p2p_2p2.连线$\overrightarrow{O_1 p_1} 和和和\overrightarrow{O_2 p_2}$ 在三维空间中交于点P,这时点O1,O2,PO_1 ,O_2,PO1,O2,P三个点可以确定一个平面,为极平面.O1,O2O_1,O_2O1,O2连线与像平面I1,I2I_1,I_2I1,I2的交点分别为e1,e2e_1,e_2e1,e2,e1,e2e_1,e_2e1,e2称为极点,O1O2O_1O_2O1O2称为基线,极平面与两个像平面I1,I2I_1,I_2I1,I2之间的相交线l1,l2l_1,l_2l1,l2称为极线.
PPP在I1I_1I1下的线号机坐标为P=[X,Y,Z]TP=[X,Y,Z]^{T}P=[X,Y,Z]T,两个投影像素点p1,p2p_1,p_2p1,p2 的像素位置满足如下公式:
{s1p1=KPs2p2=K(RP+t)\left\{ \begin{aligned}s_1p_1 =KP\\ s_2p_2=K(RP+t)\\ \end{aligned} \right. \\\\ {s1p1=KPs2p2=K(RP+t)
取 p1,p2p_1,p_2p1,p2 的归一化坐标{x1=K−1p1x2=K−1p2\left\{\begin{aligned} x_{1} =K^{-1}p_1\\ x_{2} =K^{-1}p_2\\ \end{aligned}\right.{x1=K−1p1x2=K−1p2
x1,x2x_1,x_2x1,x2是两个像素归一化平面上的坐标。代入上式,得到x2=Rx1+tx_2=Rx_1 +tx2=Rx1+t
同时左乘 t∧t^{ ∧ }t∧可得:
t∧x2=t∧Rx1t^{ ∧ }x_2=t^{ ∧ }Rx_1 t∧x2=t∧Rx1
同时左乘 x2Tx^{T}_2x2T,可得
x2Tt∧x2=x2Tt∧Rx1x^{T}_2t^{ ∧ }x_2=x^{T}_2t^{ ∧ }Rx_1 x2Tt∧x2=x2Tt∧Rx1
可得
x2Tt∧Rx1=0x^{T}_2t^{ ∧ }Rx_1=0 x2Tt∧Rx1=0
重新带入p1,p2p_1,p_2p1,p2,可得:
p2TK−Tt∧RK−1p1=0p_2^{T}K^{-T}t^{ ∧ }RK^{-1}p_1=0 p2TK−Tt∧RK−1p1=0
以上俩个式子称为对极约束,定义基础矩阵F和本质矩阵E,可以进一步简化对极约束:
E=t∧RF=K−TEK−1x2TEx1=p2TFp1=0E=t^{ ∧ }R \quad \quad \quad F=K^{-T}EK^{-1}\quad \quad \quad x^{T}_2Ex_1=p_2^{T}Fp_1=0 E=t∧RF=K−TEK−1x2TEx1=p2TFp1=0
本质矩阵E 的求解
考虑到E 的尺度等价性,可以用8对点来估计E,是为八点法.
对于一对匹配点,其归一化坐标x1=[u1,v1,1],x2=[u2,v2,1]x_1=[u_1,v_1,1],x_2=[u_2,v_2,1]x1=[u1,v1,1],x2=[u2,v2,1]根据对极约束,有
(u1,v1,1)[e1e2e3e4e5e6e7e8e9][u2v21]=0(u_1,v_1,1)\left[ \begin{matrix} e_1 &e_2 &e_3\\e_4 &e_5 &e_6 \\e_7 &e_8 &e_9 \end{matrix} \right]\left[ \begin{matrix} u_2\\v_2\\1\end{matrix} \right]=0(u1,v1,1)⎣⎡e1e4e7e2e5e8e3e6e9⎦⎤⎣⎡u2v21⎦⎤=0
把矩阵E展开为向量[e1e2e3e4e5e6e7e8e9]T\left[ \begin{matrix} e_1 &e_2 &e_3 &e_4 &e_5 &e_6 &e_7 &e_8 &e_9 \end{matrix} \right]^{T}[e1e2e3e4e5e6e7e8e9]T ,对极约束可以写成与e ee有关的线性形式:
[u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]T.e=0[u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]^{T}.e=0 [u1u2,u1v2,u1,v1u2,v1v2,v1,u2,v2,1]T.e=0
把八对点对应的x1,x2x_1,x_2x1,x2分别代入方程中,得到线性方程组:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-K9n4lOEh-1629730544222)(../AppData/Roaming/Typora/typora-user-images/1629650165462.png)]](https://img-blog.csdnimg.cn/f19e881aa226443cabb74e9d48548d2a.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0RhcmxpbmdxaWFuZw==,size_16,color_FFFFFF,t_70)
求得E后,对E进行SVD分解以求取R,t :设E的SVD分解为E=U∑VTE=U \sum V^TE=U∑VT则对应的R ,t 分别为:
t∧=URZ(π2)∑UTR=URZT(π2)∑VTt^{∧} =U R_Z(\frac{\pi}{2})\sum U^T \quad \quad R=U R^{T}_Z(\frac{\pi}{2})\sum V^T t∧=URZ(2π)∑UTR=URZT(2π)∑VT
其中RZ(π2)R_Z(\frac{\pi}{2})RZ(2π)表示沿Z轴旋转90°得到的旋转矩阵.
对极几何的讨论:
尺度不确定性: 2D图像不具有深度信息,这导致了单目视觉的尺度不确定性. 实践中设t 为单位1,计算相机运动和和特征点的3D位置,这被称为单目SLAM的初始化.
退化问题:当特征的共面或者相机发生纯旋转时,基础矩阵的自由度下降,就出现所谓的退化。实际中数据总是包含一些噪声,这时候继续使用八点法求解基础矩阵,基础矩阵多余出来的自由度将会主要由噪声决定。
为了可以避免退化现象造成的影响,通常在估计基础矩阵F的同时会求解单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵。
初始化的纯旋转问题: 若相机发生纯旋转,导致t 为零,得到的E也将为零,会导致我们无从求解R.因此单目初始化不能只有纯旋转,必须要有一定程度的平移.
多于8对点的情况:
对于八点法,有Ae=0Ae=0Ae=0,其中A为一个8×9的矩阵.
若匹配点的个数多于8个,A的尺寸变化,上述方程不成立.因此转而求取最小化二次型
mine∣∣Ae∣∣22=mineeTATAemin_e||Ae||^2_2=min_e e^TA^TAe mine∣∣Ae∣∣22=mineeTATAe
是为最小二乘意义下的E EE矩阵.
ch07 -03 3D-2D匹配: PnP(Perspective-n-Point)
2D-2D的对极几何方法需要8个或8个以上的点对(以八点法为例),且存在着初始化、纯旋转和尺度的问题。然而,如果两张图像中其中一张特征点的3D位置已知,那么最少只需3个点对(需要至少一个额外点验证结果)就可以估计相机运动。
在双目或RGB-D的视觉里程计中,我们可以直接使用PnP估计相机运动。而在单目视觉里程计中,必须先进行初始化,然后才能使用PnP。
PnP问题有多种解决方法:
- 直接线性表变换(DLT): 先求解相机位姿,再求解空间点位置
- P3P: 先求解空间点位置,再求解相机位姿
- Bundle Adjustment: 最小化重投影误差,同时求解空间点位置和相机位姿
1. 直接线性变换(DLT): 先求解相机位姿,再求解空间点位置**
考虑某个空间点P的齐次世界坐标为P=(X,Y,Z,1)P = ( X , Y , Z , 1 )P=(X,Y,Z,1) .在图像I1I_1I1中投影到特征点的归一化像素坐标x1=(u1,v1,1)x_1=(u_1,v_1,1)x1=(u1,v1,1).此时相机的位姿R ,t 是未知的,定义增广矩阵[R∣t][R|t][R∣t](不同于变换矩阵T TT)为一个3×4的矩阵,包含了旋转与平移信息,展开形式如下:
s(u1v11)=(t1t2t3t4t5t6t7t8t9t10t11t12)(XYZ1)s\left( \begin{matrix} u_1\\v_1\\1\end{matrix} \right)=\left( \begin{matrix}t_1 &t_2 &t_3 &t_4\\t_5 &t_6 &t_7 &t_8\\t_9 &t_10 &t_11&t_12 \end{matrix} \right)\left(\begin{matrix} X\\Y\\Z\\1\end{matrix} \right)s⎝⎛u1v11⎠⎞=⎝⎛t1t5t9t2t6t10t3t7t11t4t8t12⎠⎞⎝⎜⎜⎛XYZ1⎠⎟⎟⎞
用最后一行把s消去,得到两个约束:
{t1TP−t3TPu1=0t2TP−t3TPv1=0\left\{ \begin{aligned} t^{T}_1P - t^{T}_3Pu_1=0 \\ t^{T}_2P - t^{T}_3Pv_1=0 \end{aligned} \right. \\\\ {t1TP−t3TPu1=0t2TP−t3TPv1=0
其中t1=(t1,t2,t3,t4)t_1=(t_1 ,t_2 ,t_3 ,t_4)t1=(t1,t2,t3,t4),t2=(t5,t6,t7,t8)t_2=(t_5 ,t_6 ,t_7 ,t_8)t2=(t5,t6,t7,t8),t3=(t9,t10,t11,t12)t_3=(t_9 ,t_10 ,t_11 ,t_12)t3=(t9,t10,t11,t12).t1,t2,t3t_1,t_2,t_3t1,t2,t3为待求量.
将N对匹配的特征点代入方程中,得到线性方程组:
(P1T0−U1P1T0P1T−U1P1TPNT0−UNPNT0PNT−UNPNT)\left( \begin{matrix} P^{T}_1 &0 & -U_1P^{T}_1\\ 0 & P^{T}_1 & -U_1P^{T}_1 \\ P^{T}_N &0 & -U_NP^{T}_N\\ 0 & P^{T}_N &-U_NP^{T}_N\end{matrix} \right)⎝⎜⎜⎛P1T0PNT00P1T0PNT−U1P1T−U1P1T−UNPNT−UNPNT⎠⎟⎟⎞
只需6对匹配点即可求解增广矩阵[ R ∣ t ] ,若匹配点数多于6对时,可以求最小二乘解.对于求解出的旋转矩阵R,可以通过QR分解等手段将其投影到S E ( 3 ) 上.
2. P3P: 先求解空间点位置,再求解相机位姿
这里要说明的是在场景1中,我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点,因此求得的是相机(相机坐标系)相对于真实物体(世界坐标系)的位姿,如图所示:
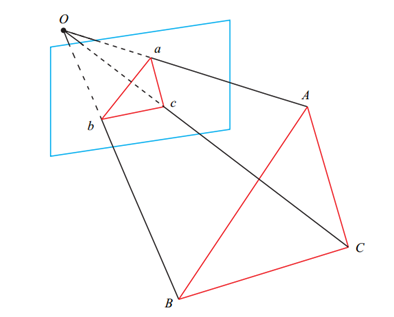
而在场景2中,通常输入的是上一帧中的3D点(在上一帧的相机坐标系下表示的点)和这些3D点在当前帧中的投影得到的2D点,所以它求得的是当前帧相对于上一帧的位姿变换,如图所示:
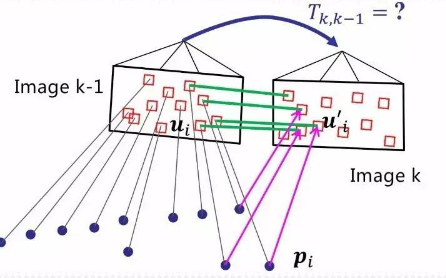
两种情况本质上是相同的,都是基于已知3D点和对应的图像2D点求解相机运动的过程。下面详细探讨P3P的求解过程。
已知3对匹配点的世界坐标A ,B ,C 和投影坐标a ,b ,c ,根据三角形的余弦定理,有
{OA2+OB2−2OA⋅OB⋅cos<a,b>=AB2OB2+OC2−2OB⋅OC⋅cos<b,c>=BC2OA2+OC2−2OA⋅OC⋅cos<a,c>=AC2\left\{ \begin{aligned} OA^2+OB^2-2OA \cdot OB\cdot cos<a,b>=AB^2 \\ OB^2+OC^2-2OB \cdot OC\cdot cos<b,c>=BC^2 \\ OA^2+OC^2-2OA \cdot OC\cdot cos<a,c>=AC^2 \\ \end{aligned} \right. \\\\ ⎩⎪⎨⎪⎧OA2+OB2−2OA⋅OB⋅cos<a,b>=AB2OB2+OC2−2OB⋅OC⋅cos<b,c>=BC2OA2+OC2−2OA⋅OC⋅cos<a,c>=AC2
记x=OA/OC,y=OB/OC,u=BC2/AB2,v=AC2/AB2x=OA/OC,y = OB / OC ,u = BC^2 / AB^2 ,v=AC^2/AB^2x=OA/OC,y=OB/OC,u=BC2/AB2,v=AC2/AB2
{(1−u)y2−ux2−cos<b,c>y+2uxycos<a,b>+1=0(1−w)x2−wy2−cos<a,c>y+2wxycos<a,b>+1=0\left\{ \begin{aligned} (1-u)y^2-ux^2-cos<b,c>y+2uxycos<a,b> + 1=0\\ (1-w)x^2-wy^2-cos<a,c>y+2wxycos<a,b> + 1=0\\ \end{aligned} \right. {(1−u)y2−ux2−cos<b,c>y+2uxycos<a,b>+1=0(1−w)x2−wy2−cos<a,c>y+2wxycos<a,b>+1=0
上式中,三个余弦角cos⟨a,b⟩,cos⟨b,c⟩,cos⟨a,c⟩\cos \langle a,b \rangle ,\cos \langle b,c \rangle,\cos \langle a,c \ranglecos⟨a,b⟩,cos⟨b,c⟩,cos⟨a,c⟩以及u uu,v vv是已知的,可以求解出x ,y 进而求解出A ,B ,C 三点的相机坐标.然后根据3D-3D的点对,计算相机的运动R ,t .
3. Bundle Adjustment: 最小化重投影误差,同时求解空间点位置和相机位姿
设相机位姿变换矩阵T ,某空间点的世界坐标 Pi=[X,Y,Z]TP_i=[X,Y,Z]^TPi=[X,Y,Z]T, 其投影的像素坐标为 ui=[ui,vi]Tu_i=[u_i,v_i]^Tui=[ui,vi]T ,像素位置与空间点位置的关系如下:
siui=KTPis_iu_i=KTP_i siui=KTPi
由于相机位姿未知及观测点的噪声,上式存在一个误差,称为重投影误差$ \displaystyle e=u_i-\frac{1}{s_i}KTP_i$因此我们对重投影误差求和,寻找最好的相机位姿和特征点的空间位置,最小化重投影误差:
T∗=argminT12∑i=1n∣∣ui−1siKTPi∣∣2Pi∗=argminPi12∑i=1n∣∣ui−1siKTPi∣∣2T^*=\quad argmin_T \frac{1}{2}\sum^n_{i=1}||u_i-\frac{1}{s_i}KTP_i||^2\\ P_i^*=\quad argmin_{P_i} \frac{1}{2}\sum^n_{i=1}||u_i-\frac{1}{s_i}KTP_i||^2 T∗=argminT21i=1∑n∣∣ui−si1KTPi∣∣2Pi∗=argminPi21i=1∑n∣∣ui−si1KTPi∣∣2
使用最小二乘优化,要分别求e对T和P的导数:
e(x+Δx)≈e(x)+JΔxe(x + \Delta x) \approx e(x)+J\Delta x e(x+Δx)≈e(x)+JΔx
求e 对T 的导数:当e为像素坐标误差(2维),x为相机位姿(6维)时,J将是一个2×6的矩阵.我们来推导J的形式:
取中间变量P′=(TP)1:3=[X′,Y′,Z′]TP' = (TP)_{1:3}=[X',Y',Z']^TP′=(TP)1:3=[X′,Y′,Z′]T使用李代数求导的扰动模型,对T左乘微小扰动δξ\delta \xiδξ,求导得到:
∂e∂δξ=limδξ=0e(δξ⊕ξ)−e(ξ)δξ=∂e∂P‘∂P‘∂δξ\displaystyle\frac{\partial e}{\partial \delta \xi} =lim_{\delta \xi=0} \frac{e(\delta \xi\oplus \xi)-e( \xi)}{\delta \xi} = \frac{\partial e}{\partial {P^{‘}}}\frac{\partial {P^{‘}}}{\partial \delta \xi} ∂δξ∂e=limδξ=0δξe(δξ⊕ξ)−e(ξ)=∂P‘∂e∂δξ∂P‘
其中,$\oplus $ 表示李代数的左乘扰动 ,其中 第一项 $ \displaystyle \frac{\partial e}{\partial P^{‘}}$:该误差表示误差关于投影点的导数:
∂e∂P‘=−(∂u∂X‘∂u∂Y‘∂u∂Z‘∂v∂X‘∂v∂Y‘∂v∂Z‘)=−(fxZ‘0−fxX‘Z‘20fyZ‘−fxY‘Z‘2)\frac{\partial e}{\partial P^{‘}}=-\left( \begin{matrix} \frac{\partial u}{\partial X^{‘}} & \frac{\partial u}{\partial Y^{‘} } &\frac{\partial u}{\partial Z^{‘}}\\ \frac{\partial v}{\partial X^{‘}} & \frac{\partial v}{\partial Y^{‘} } &\frac{\partial v}{\partial Z^{‘}} \end{matrix} \right)=-\left( \begin{matrix} \frac{f_x}{ Z^{‘}} & 0 &-\frac{f_xX^{‘}}{ Z^{‘2}} \\ 0 & \frac{f_y}{ Z^{‘}} &-\frac{f_xY^{‘}}{ Z^{‘2}} \end{matrix} \right)∂P‘∂e=−(∂X‘∂u∂X‘∂v∂Y‘∂u∂Y‘∂v∂Z‘∂u∂Z‘∂v)=−(Z‘fx00Z‘fy−Z‘2fxX‘−Z‘2fxY‘)
第二项∂P‘∂δξ\displaystyle \frac{\partial {P^{‘}}}{\partial \delta \xi}∂δξ∂P‘ 为变换后的点关于李代数的导数:
∂P‘∂δξ=TP∂δξ=(TP)⨀=∂e∂P‘=−(I−P0T0T)\displaystyle \frac{\partial {P^{‘}}}{\partial \delta \xi}=\frac{TP}{\partial \delta \xi} =(TP)^{\bigodot} = \frac{\partial e}{\partial P^{‘}}=-\left( \begin{matrix} I &-P \\ 0^T &0^T \end{matrix} \right)∂δξ∂P‘=∂δξTP=(TP)⨀=∂P‘∂e=−(I0T−P0T)
而在P′P^{'}P′的定义中,取出前3维,于是得到:∂P‘∂δξ=TP∂δξ=(TP)⨀=[I,−P]\displaystyle \frac{\partial {P^{‘}}}{\partial \delta \xi}=\frac{TP}{\partial \delta \xi} =(TP)^{\bigodot} =[I,-P]∂δξ∂P‘=∂δξTP=(TP)⨀=[I,−P]而
()\left( \begin{matrix} \end{matrix} \right)()
P′∧=(0Z′−Y′−Z′0X′Y′−X′0)P^{'\wedge}= \left( \begin{matrix} 0 &Z^{'} &-Y^{'}\\ -Z^{'} &0 &X^{'}\\ Y^{'} &-X^{'} &0 \end{matrix} \right)P′∧=⎝⎛0−Z′Y′Z′0−X′−Y′X′0⎠⎞将两项相乘,得到了2×6的雅可比矩阵JT\displaystyle J^TJT,求e 对P的导数可得结果如下:
JT=∂e∂δξ=(fxZ‘0−fxX‘Z‘2−fxX‘Y‘Z‘2fx+fxX‘2Z‘2−fxY‘Z‘0fYZ‘−fyY‘Z‘2−fy−fyYX‘2Z‘2fyY‘X‘Z‘2fyX‘Z‘)J^T=\frac{\partial e}{\partial \delta \xi} =\displaystyle \left( \begin{matrix} \frac{f_x}{ Z^{‘}} & 0 &-\frac{f_xX^{‘}}{ Z^{‘2}} &-\frac{f_xX^{‘}Y^{‘}}{ Z^{‘2}} & f_x+\frac{f_xX^{‘2}}{ Z^{‘2}} &-\frac{f_xY^{‘}}{ Z^{‘}} \\ 0 &\frac{f_Y}{ Z^{‘}} &-\frac{f_yY^{‘}}{ Z^{‘2}} &-f_y-\frac{f_yYX^{‘2}}{ Z^{‘2}} &\frac{f_yY^{‘}X^{‘}}{ Z^{‘2}} &\frac{f_yX^{‘}}{ Z^{‘}} \end{matrix} \right)JT=∂δξ∂e=(Z‘fx00Z‘fY−Z‘2fxX‘−Z‘2fyY‘−Z‘2fxX‘Y‘−fy−Z‘2fyYX‘2fx+Z‘2fxX‘2Z‘2fyY‘X‘−Z‘fxY‘Z‘fyX‘)**该Jocabi矩阵描述了,重投影误差关于相机位姿李代数的一阶变化关系。**前面有负号的原因是 该误差由观测值减预测值得到。
特征点位置的优化,需要求解e对空间点P的导数,由链式法则可得:
∂e∂P=∂e∂P‘∂P‘∂P\frac{\partial e}{\partial P}=\frac{\partial e}{\partial P^{‘}} \frac{\partial P^{‘}}{\partial P} ∂P∂e=∂P‘∂e∂P∂P‘
第一项误差关于投影点的导数已经得到,关于第二项∂P‘∂P\displaystyle\frac{\partial P^{‘}}{\partial P}∂P∂P‘,按照定义
P‘=exp(ξ∧)P=RP+tP^{‘} =exp(\xi^{\wedge})P=RP+t P‘=exp(ξ∧)P=RP+t
求导后为可得:
P‘=RP^{‘} =R P‘=R
所所以∂e∂P\displaystyle \frac{\partial e}{\partial P}∂P∂e为:
∂e∂P=−(fxZ‘0−fxX‘Z‘20fyZ‘−fxY‘Z‘2)\displaystyle \frac{\partial e}{\partial P} = -\left( \begin{matrix} \frac{f_x}{ Z^{‘}} & 0 &-\frac{f_xX^{‘}}{ Z^{‘2}} \\ 0 & \frac{f_y}{ Z^{‘}} &-\frac{f_xY^{‘}}{ Z^{‘2}} \end{matrix} \right)∂P∂e=−(Z‘fx00Z‘fy−Z‘2fxX‘−Z‘2fxY‘)
小姐:
由以上两个大的步骤我们推导得到 观测相机方程关于相机位姿与特征点的两个导数矩阵。
4.EPnP求解位姿
详细见OPenCV提供的EPnP求PnP问题,然后通过G2O优化求解,见十四讲P165.
ch07 -04 3D-3D匹配: ICP
对于一组已配对好的3D点:
P=p1,⋯,pn,P′=p1′,⋯,pn′P={p_1,⋯,p_n},P′={p_1′,⋯,p_n′} P=p1,⋯,pn,P′=p1′,⋯,pn′
现在,想要找一个欧氏变换R ,t ,使得:
∀i,pi=Rpi′+t∀ i,p_i=Rp_i′+t ∀i,pi=Rpi′+t
ICP问题的求解包含两种方式:
- 利用线性代数的求解(主要是SVD)
- 利用非线性优化方式的求解(类似于Bundle Adjustment)
1. SVD方法
定义第 i对点的误差项为ei=pi−(Rpi′+t)e_i = p_i - (R p'_i + t)ei=pi−(Rpi′+t),定义两组点的质心p=1n∑i=1n(pi),p′=1n∑i=1n(pi′)p = \frac{1}{n} \sum_{i=1}^n (p_i),p' = \frac{1}{n} \sum_{i=1}^n (p'_i)p=n1∑i=1n(pi),p′=n1∑i=1n(pi′)
构建最小二乘问题,求取最合适的 R, t.
minR,tJ=12∣∣(pi−((Rpi′+t)))∣∣22=12∣∣(pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2min_{R,t}J=\frac{1}{2}||(p_i-((R p'_i + t)))||_2^2\\ = \frac{1}{2}||(p_i-p-R (p'_i - p')||^2+||p-Rp'-t||^2 minR,tJ=21∣∣(pi−((Rpi′+t)))∣∣22=21∣∣(pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2
左边只和旋转矩阵R相关,而右边既有 R也有t,但只和质心相关.因此令左边取最小值解出R,代入到右边令式子等于0求出t.
定义去质心坐标qi=pi−p,qi′=pi′−p′q i = p i − p , \quad \quad q'_i=p'_i-p'qi=pi−p,qi′=pi′−p′ 则优化目标可写成:
R∗=minR∑i=1n∣∣(pi−p−R(pi′−p′)∣∣2=minR∑i=1n−qiTRqi′=−tr(R∑i=1nqi′qiT)R^* =min_R \sum ^n_{i=1}||(p_i-p-R (p'_i - p')||^2 \\ =min_R \sum ^n_{i=1}-q_i^TRq_i' \\ =-tr(R \sum ^n_{i=1}q_i'q_i^T) R∗=minRi=1∑n∣∣(pi−p−R(pi′−p′)∣∣2=minRi=1∑n−qiTRqi′=−tr(Ri=1∑nqi′qiT)
省略数学证明,定义矩阵:
W=∑i=1nqiqi′TW =\sum ^n_{i=1}q_iq_i^{'T} W=i=1∑nqiqi′T
对矩阵W WW进行SVD分解得到:
W=UΣVTW=UΣVT W=UΣVT
可求解
R=UVTR=UV^T R=UVT
2. 非线性优化方法
使用李代数表达表达位姿,目标函数可以写成
minξ=12∑i−1n∣∣(pi−exp(ξ∧)p′)∣∣22min_\xi =\frac{1}{2}\sum^n_{i-1} ||(p_i-exp(\xi^{\wedge})p')||^2_2 minξ=21i−1∑n∣∣(pi−exp(ξ∧)p′)∣∣22
误差项关于位姿的导数可以用李代数求导的扰动模型,计算导数得到:
∂P∂δξ=−(exp(ξ∧)pi′)⨀\displaystyle \frac{\partial {P^{}}}{\partial \delta \xi} =-(exp(\xi^{\wedge})p'_i)^{\bigodot}∂δξ∂P=−(exp(ξ∧)pi′)⨀
对于一组已配对好的3D点:
P=p1,⋯,pn,P′=p1′,⋯,pn′P={p_1,⋯,p_n},P′={p_1′,⋯,p_n′} P=p1,⋯,pn,P′=p1′,⋯,pn′
现在,想要找一个欧氏变换R ,t ,使得:
∀i,pi=Rpi′+t∀ i,p_i=Rp_i′+t ∀i,pi=Rpi′+t
ICP问题的求解包含两种方式:
- 利用线性代数的求解(主要是SVD)
- 利用非线性优化方式的求解(类似于Bundle Adjustment)
3. SVD方法求解
定义第 i对点的误差项为ei=pi−(Rpi′+t)e_i = p_i - (R p'_i + t)ei=pi−(Rpi′+t),定义两组点的质心p=1n∑i=1n(pi),p′=1n∑i=1n(pi′)p = \frac{1}{n} \sum_{i=1}^n (p_i),p' = \frac{1}{n} \sum_{i=1}^n (p'_i)p=n1∑i=1n(pi),p′=n1∑i=1n(pi′)
构建最小二乘问题,求取最合适的 R, t.
minR,tJ=12∣∣(pi−((Rpi′+t)))∣∣22=12∣∣(pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2min_{R,t}J=\frac{1}{2}||(p_i-((R p'_i + t)))||_2^2\\ = \frac{1}{2}||(p_i-p-R (p'_i - p')||^2+||p-Rp'-t||^2 minR,tJ=21∣∣(pi−((Rpi′+t)))∣∣22=21∣∣(pi−p−R(pi′−p′)∣∣2+∣∣p−Rp′−t∣∣2
左边只和旋转矩阵R相关,而右边既有 R也有t,但只和质心相关.因此令左边取最小值解出R,代入到右边令式子等于0求出t.
定义去质心坐标qi=pi−p,qi′=pi′−p′q i = p i − p , \quad \quad q'_i=p'_i-p'qi=pi−p,qi′=pi′−p′ 则优化目标可写成:
R∗=minR∑i=1n∣∣(pi−p−R(pi′−p′)∣∣2=minR∑i=1n−qiTRqi′=−tr(R∑i=1nqi′qiT)R^* =min_R \sum ^n_{i=1}||(p_i-p-R (p'_i - p')||^2 \\ =min_R \sum ^n_{i=1}-q_i^TRq_i' \\ =-tr(R \sum ^n_{i=1}q_i'q_i^T) R∗=minRi=1∑n∣∣(pi−p−R(pi′−p′)∣∣2=minRi=1∑n−qiTRqi′=−tr(Ri=1∑nqi′qiT)
省略数学证明,定义矩阵:
W=∑i=1nqiqi′TW =\sum ^n_{i=1}q_iq_i^{'T} W=i=1∑nqiqi′T
对矩阵W WW进行SVD分解得到:
W=UΣVTW=UΣVT W=UΣVT
可求解
R=UVTR=UV^T R=UVT
4. 非线性优化方法求解
使用李代数表达表达位姿,目标函数可以写成
minξ=12∑i−1n∣∣(pi−exp(ξ∧)p′)∣∣22min_\xi =\frac{1}{2}\sum^n_{i-1} ||(p_i-exp(\xi^{\wedge})p')||^2_2 minξ=21i−1∑n∣∣(pi−exp(ξ∧)p′)∣∣22
误差项关于位姿的导数可以用李代数求导的扰动模型,计算导数得到:
∂P∂δξ=−(exp(ξ∧)pi′)⨀\displaystyle \frac{\partial {P^{}}}{\partial \delta \xi} =-(exp(\xi^{\wedge})p'_i)^{\bigodot}∂δξ∂P=−(exp(ξ∧)pi′)⨀
可以直接使用最小二乘优化方法求解位姿.
相关文章:
12、OpenCV实现图像的空间滤波——图像平滑
1、空间滤波基础概念 1、空间滤波基础 空间滤波一词中滤波取自数字信号处理,指接受或拒绝一定的频率成分,但是空间滤波学习内容实际上和通过傅里叶变换实现的频域的滤波是等效的,故而也称为滤波。空间滤波主要直接基于领域(空间域…

计算 LBP 特征
#include <opencv2/opencv.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/features2d/features2d.hpp> #include <opencv2/features2d/features2d.hpp> // 计算原始LBP特征 cv::Mat OLBP(cv::Mat& srcImage) {const int nRows …

三维重建【四】-------------------结构光 三维重建----论文调研
1. 动态目标实时三维重建-结构光方案 动态目标 三维重建 Stripe boundary codes for real-time structured-light range scanning of moving objects 我们提出了一种新的实时结构光扫描方法。在分析现有结构光技术的基本假设之后,我们基于编码投影条纹之间的边界&…

APP开发定制
app是什么意思? APP,application的简称,是智能手机的第三方应用程序,常见的有微信、手机qq、今日头条、手机支付宝、腾讯视频、微店等,随着智能手机和ipad等移动终端设备的普及,人们逐渐习惯了使用APP客户端上网的方式…

Haar 特征提取
double HaarExtract(double const ** image ,int type_, cv::Rect roi) {double value;double wh1, wh2;double bk1, bk2;int x roi.x;int y roi.y;int width roi.width;int height roi.height;switch (type_){// Haar水平边缘case 0: // HaarHEdgewh1 calcIntegral(image…

awk的基本⽤法
awk的基本⽤法 awk是报告⽣成器,格式化⽂本输出,有多种版本。centos中的是gawk即GNU awk版本。 awk⼯作原理:第⼀步:执⾏BEGIN{action;...}语句块中的语句。第⼆步:从⽂件或标准输⼊(stdin)读取…
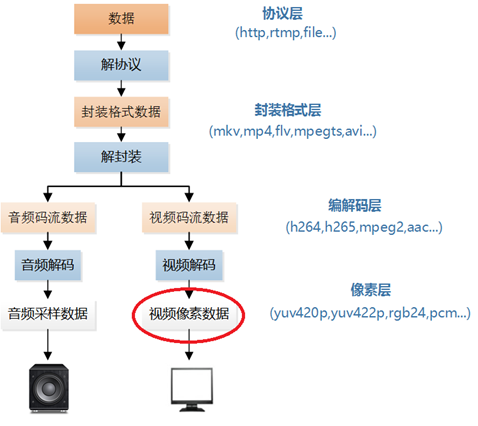
视音频数据处理入门:RGB、YUV像素数据处理【转】
转自:http://blog.csdn.net/leixiaohua1020/article/details/50534150 视音频数据处理入门系列文章: 视音频数据处理入门:RGB、YUV像素数据处理 视音频数据处理入门:PCM音频采样数据处理 视音频数据处理入门:H.264视频…
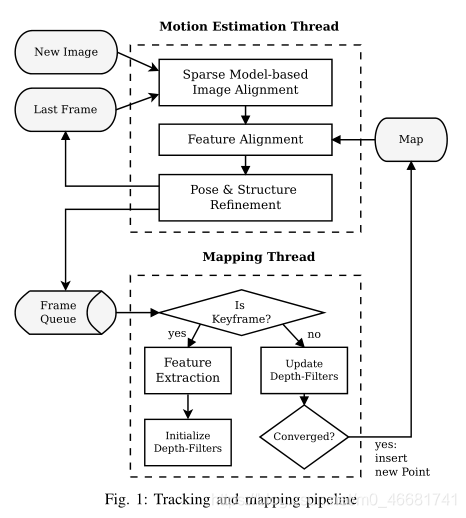
SVO(SVO: fast semi-direct monocular visual odometry)
SVO(SVO: fast semi-direct monocular visual odometry)翻译 文章目录SVO(SVO: fast semi-direct monocular visual odometry)翻译1、介绍2、系统概述3、符号4、运动估计4.1、 基于稀疏模型的图像对齐4.2、 通过特征对齐松弛4.3、…

MSER 候选车牌区域检测
#include "opencv2/highgui/highgui.hpp" #include "opencv2/features2d/features2d.hpp" #include "opencv2/imgproc/imgproc.hpp" #include <iostream> // Mser车牌目标检测 std::vector<cv::Rect> mserGetPlate(cv::Mat srcImage…

从HelloWorld看Knative Serving代码实现
为什么80%的码农都做不了架构师?>>> 摘要: Knative Serving以Kubernetes和Istio为基础,支持无服务器应用程序和函数的部署并提供服务。我们从部署一个HelloWorld示例入手来分析Knative Serving的代码细节。 概念先知 官方给出的这…
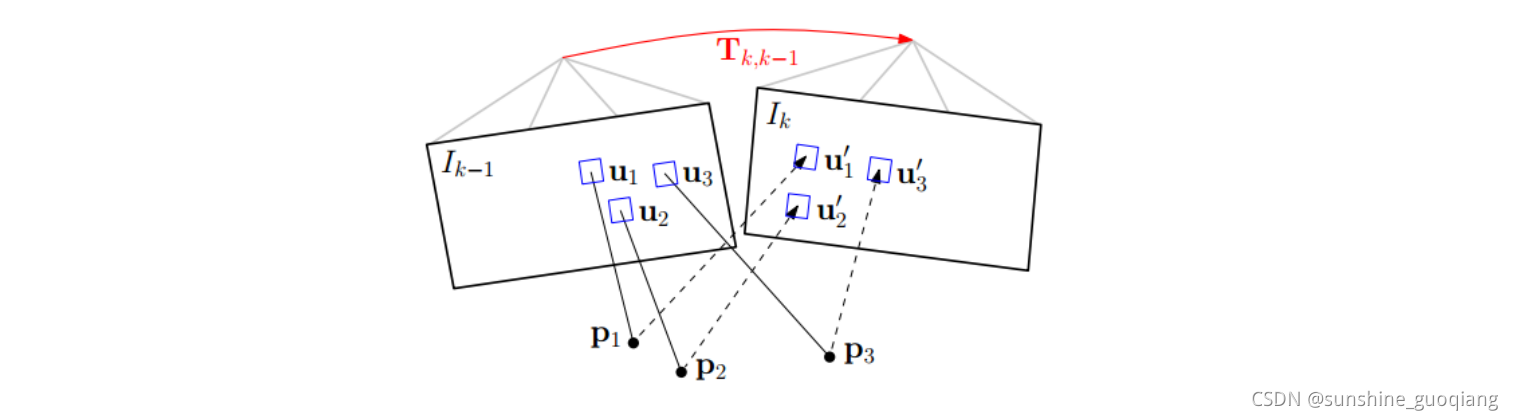
svo_note
SVO论文笔记1.frame overviews2. Motion Estimate Thread2.1 Sparse Model-based Image Alignment 基于稀疏点亮度的位姿预估2.2 Relaxation Through Feature Alignment 基于图块的特征点匹配2.3 Pose and Structure Refinement3 Mapping Thread3.1 depth-filter3.2 初始化参考…

Druid 配置 wallfilter
这个文档提供基于Spring的各种配置方式 使用缺省配置的WallFilter <bean id"dataSource" class"com.alibaba.druid.pool.DruidDataSource" init-method"init" destroy-method"close">...<property name"filters" v…
vue下的bootstrap table + jquery treegrid, treegrid无法渲染的问题
在mian.js导入的包如下:该bootstrap-table-treegrid.js需要去下载,在复制到jquery-treegrid/js/ 1 import $ from jquery 2 import bootstrap/dist/css/bootstrap.min.css 3 import bootstrap/dist/js/bootstrap.min 4 import bootstrap-table/dist/boot…

内存和缓存的区别
今天看书的时候又看到了内存和缓存,之所以说又,是因为之前遇到过查过资料,但是现在又忘了(图侵删)。 所以又复习一遍,记录一下,有所纰漏的地方,欢迎指正。 同志们,上图并不是内存和缓存中的任何…

【Boost】noncopyable:不可拷贝
【CSDN】:boost::noncopyable解析 【Effective C】:条款06_若不想使用编译器自动生成地函数,就该明确拒绝 1.example boost::noncopyable 为什么要boost::noncopyable 在c中定义一个类的时候,如果不明确定义拷贝构造函数和拷贝赋…

BigData NoSQL —— ApsaraDB HBase数据存储与分析平台概览
一、引言时间到了2019年,数据库也发展到了一个新的拐点,有三个明显的趋势: 越来越多的数据库会做云原生(CloudNative),会不断利用新的硬件及云本身的优势打造CloudNative数据库,国内以阿里云的Cloud HBase、POLARDB为代…

ubuntu clion 创建桌面快捷方式
ubuntu clion 创建桌面快捷方式 首先在终端下输入 cd /usr/share/applications/进入applications目录下,建立一个clion.desktop文件 sudo touch clion.desktop然后在vim命令下编辑该文件 sudo vim clion.desktop进入vim后,按i插入开始编辑该文件&…

Flex 布局:语法篇
2019独角兽企业重金招聘Python工程师标准>>> 布局的传统解决方案,基于盒状模型,依赖 display 属性 position 属性 float 属性。它对于那些特殊布局非常不方便,比如,垂直居中就不容易实现。 2009年,W3C 提…

特征运动点估计
cv::Mat getRansacMat(const std::vector<cv::DMatch>& matches, const std::vector<cv::KeyPoint>& keypoints1, const std::vector<cv::KeyPoint>& keypoints2, std::vector<cv::DMatch>& outMatches) {// 转换特征点格式std::vecto…

Vue+Element-ui+二级联动封装组件
通过父子组件传值 父组件: 1 <template>2 <linkage :citysList"citysList" :holder"holder" saveId"saveId"></linkage>3 </template>4 <script>5 import linkage from ./common/linkage6 export de…

MOG2 成员函数参数设定
pMOG2->setDetectShadows(true); // 背景模型影响帧数 默认为500 pMOG2->setHistory(1000); // 模型匹配阈值 pMOG2->setVarThreshold(50); // 阴影阈值 pMOG2->setShadowThreshold(0.7);前景中模型参数,设置为0表示背景,255为前景ÿ…

webpack 大法好 ---- 基础概念与配置(1)
再一次见面! Light 还是太太太懒了,距离上一篇没啥营养的文章已经过去好多天。今天为大家介绍介绍 webpack 最基本的概念,以及简单的配置,让你能快速得搭建一个可用的 webpack 开发环境。 webpack的安装 webpack 运行于 node 环境…

Zookeeper迁移(扩容/缩容)
zookeeper选举原理在迁移前有必要了解zookeeper的选举原理,以便更科学的迁移。快速选举FastLeaderElectionzookeeper默认使用快速选举,在此重点了解快速选举:向集群中的其他zookeeper建立连接,并且只有myid比对方大的连接才会被接…

SVO Without ROS环境搭建
Installation: Plain CMake (No ROS) 首先,建立工作目录:workspace,然后把下面的需要的都在该目录下进行. mkdir workspace cd workspace Boost - c Librairies (thread and system are needed) sudo apt-get install libboost-all-dev Eige…

BackgroundSubtractorGMG 背景建模
#include <opencv2/bgsegm.hpp> #include <opencv2/video.hpp> #include <opencv2/opencv.hpp> #include <iostream> #include <sstream> using namespace cv; using namespace std; using namespace bgsegm; // GMG目标建模检测 void detectBac…

启动webpack-dev-server只能本机访问的解决办法
修改package.json的dev启动设置,增加--host 0.0.0.0启动后localhost更换为本机IP即可访问

TCP/IP:IP选项处理
引言 IP输入函数要对IP 进行选项处理,。RFC791和1122规定了IP选项和处理规则。一个IP首部可以跟40个字节的选项。 选项格式 选项的格式,分为两种类型,单字节和多字节。 ip_dooptions函数 这个函数用于判断分组转发。用常量位移访问IP选项字段…

【SVO2.0 安装编译】Ubuntu 20.04 + Noetic
ways one 链接: https://pan.baidu.com/s/1ZAkeD64wjFsDHfpCm1CB1w 提取码: kxx2 (downloads and use idirectly) ways two: [SVO2-OPEN: https://github.com/uzh-rpg/rpg_svo_pro_open](https://github.com/DEARsunshine/rpg_svo_pro_open)git挂梯子 如果各位终端无法挂梯…

人眼目标检测初始化
// 初始化摄像头读取视频流cv::VideoCapture cap(0);// 宽高设置为320*256cap.set(CV_CAP_PROP_FRAME_WIDTH, 320);cap.set(CV_CAP_PROP_FRAME_HEIGHT, 256);// 读取级联分类器// 文件存放在opencv\sources\data\haarcascades bool flagGlasses false;if(flagGlasses){face_ca…
Qt之界面换肤
简述 常用的软件基本都有换肤功能,例如:QQ、360、迅雷等。换肤其实很简单,并没有想象中那么难,利用前面分享过的QSS系列文章,沃我们完全可以实现各种样式的定制! 简述实现原理效果新建QSS文件编写QSS代码加…
