当前位置：首页 > 编程日记 > 正文

Leetcode算法系列| 11. 盛最多水的容器

编程日记 2024-01-05 10:51:13

1.题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

示例1:

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：
- n == height.length
- 2 <= n <= 10^5
- <= height[i] <= 10^4

2.题解

C# 解法一：暴力

这题让我们求两个柱线间能存放的最大空间是多少，第一种解法当然就是暴力啦！我们遍历这个height数组，对每一个位置对我们计算从当前位置到后面的每个柱子间所能存水的数量，如果找出每个位置的最大值，如果比当前的最大值大，则更新，否则不更新。

public class Solution {
    public int MaxArea(int[] height)
   {
       int res = 0;
       for (int i = 0; i < height.Length; i++)
       {
           for (int j = i + 1; j < height.Length; j++)
           {
               int thisArea = (j - i) * Math.Min(height[i], height[j]);
               res = Math.Max(res, thisArea);
           }
       }
       return res;
   }
}

时间复杂度：O(n^2)
- 有一个双层循环，外层循环从0到height.Length-1，内层循环从i+1到height.Length-1。对于每一个i，内层循环会执行height.Length - i - 1次。因此，总的时间复杂度是这两层循环的乘积。
空间复杂度：O(1)
- 只使用了几个整数变量来存储中间结果和最终结果，因此，它的空间复杂度是常数级别的，即：
  (O(1))

C# 解法二：双指针（左指针大于右指针，left++）

本题是一道经典的面试题，最优的做法是使用「双指针」。如果第一次看到这题，不一定能想出双指针的做法。
双指针代表的是可以作为容器边界的所有位置的范围。在一开始，双指针指向数组的左右边界，表示数组中所有的位置都可以作为容器的边界，因为我们还没有进行过任何尝试。在这之后，我们每次将对应的数字较小的那个指针往另一个指针的方向移动一个位置，就表示我们认为这个指针不可能再作为容器的边界了。
我们每次以双指针为左右边界（也就是「数组」的左右边界）计算出的容量中的最大值。
定义两个指针，一个指向数组的开头，一个指向数组的结尾。然后计算两个指针所指向的元素所构成的容器的面积，并记录下最大的面积。然后根据两个指针所指向的元素的大小，移动指针，直到两个指针相遇。

public class Solution {
     public int MaxArea(int[] height)
   {
       int res = 0;
       int left = 0; int right = height.Length - 1;
       while (left < right)
       {
           int thisArea = (right - left) * Math.Min(height[left], height[right]);
           res = Math.Max(res, thisArea);
           if (height[left] > height[right]) right--;
           else left++;
       }
       return res;
    }
}

时间复杂度：O(n)
- 双指针总计最多遍历整个数组一次。
空间复杂度：O(1)
- 只需要额外的常数级别的空间。

C# 解法三：双指针优化（左指针小于等于最小高度，left++）

public class Solution {
     public int MaxArea(int[] height)
    {
        int res = 0;
        int left = 0; int right = height.Length - 1;
        while (left < right)
        {
            int minHeight = Math.Min(height[left], height[right]);
            int thisArea = (right - left) * minHeight;
            res = Math.Max(res, thisArea);
            if (left < right && height[left] <= minHeight) left++;
            if (left < right && height[right] <= minHeight) right--;
        }
        return res;
    }
}

时间复杂度：O(n)
- 双指针总计最多遍历整个数组一次。
空间复杂度：O(1)
- 只需要额外的常数级别的空间。

Java 解法一：双指针

public class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int ans = 0;
        while (l < r) {
            int area = Math.min(height[l], height[r]) * (r - l);
            ans = Math.max(ans, area);
            if (height[l] <= height[r]) {
                ++l;
            }
            else {
                --r;
            }
        }
        return ans;
    }
}

时间复杂度：O(n)
- 双指针总计最多遍历整个数组一次。
空间复杂度：O(1)
- 只需要额外的常数级别的空间。

Python3 解法一：双指针

class Solution:
    def maxArea(self, height: List[int]) -> int:
        l, r = 0, len(height) - 1
        ans = 0
        while l < r:
            area = min(height[l], height[r]) * (r - l)
            ans = max(ans, area)
            if height[l] <= height[r]:
                l += 1
            else:
                r -= 1
        return ans

时间复杂度：O(n)
- 双指针总计最多遍历整个数组一次。
空间复杂度：O(1)
- 只需要额外的常数级别的空间。

Leetcode算法系列算法leetcodec#unity数据结构

https://www.dkcj.cn/info/598.html

Math: Math.atan() 与 Math.atan2() 计算两点间连线的夹角

Math.atan2()函数返回点(x,y)和原点(0,0)之间直线的倾斜角.那么如何计算任意两点间直线的倾斜角呢?只需要将两点x,y坐标分别相减得到一个新的点(x2-x1,y2-y1).然后利用他求出角度就可以了.使用下面的一个转换可以实现计算出两点间连线的夹角.然而,Math.atan()只能返回一个角度值,因此确定他的角度非常的复杂,而且,90度和270度的正切是无穷大,因为除数为零,我们也是比较难以处理的~!angel为一个角度的弧度值,slope为直线的斜率,是一个数字,这个数字可以是负的。

编程日记2024/02/24 00:00:05

Integer.toHexString(b & 0xff)理解以及& 0xff什么意思

首先toHexString传的参数应该是int类型32位，此处传的是byte类型8位，所以前面需要补24个0。然后& 0xff 就是把前面24个0去掉只要后8位。toHexString(b & 0xff)相当于做了一次位的与运算，将前24位字符省略，将后8位保留。是两个十六进制的数,每个f用二进制表示是1111,所以占四位（bit）,两个f（）占八位（bit），八位（bit）也就是一个字节（byte）.这个方法是把字节（转换成了int）以16进制的方式显示。我的理解是这样，如有不对欢迎指正！

编程日记2024/02/14 01:00:01

CSS局限属性contain：优化渲染性能的利器

在网页开发中，优化渲染性能是一个重要的目标。CSS局限属性contain是一个强大的工具，可以帮助我们提高网页的渲染性能。本文将介绍contain属性的基本概念、用法和优势，以及如何使用它来优化网页的渲染过程。

编程日记2024/02/02 15:11:24

【OpenCV】在Linux上使用OpenCvSharp

OpenCvSharp是一个OpenCV的 .Net wrapper，应用最新的OpenCV库开发，使用习惯比EmguCV更接近原始的OpenCV，该库采用LGPL发行，对商业应用友好。

精选2024/01/31 20:42:49

在C#中调用C++函数并返回const char*类型的值

在C#中，使用DllImport特性将C++函数声明为外部函数。在Main方法中，调用generateProjectCode函数并将返回的指针转换为const char*类型的字符串。在C#中调用C++函数并返回const char*类型的值，可以使用Interop服务来实现。C++代码需要编译为动态链接库（DLL）。

编程日记2024/01/22 15:18:55

C#winform上位机开发学习笔记3-串口助手的信息保存功能添加

上位机开发的系列学习笔记，避免遗忘多记录多补充多优化

编程日记2024/01/20 22:24:35

Java数据结构与算法：排序算法之插入排序

插入排序是一种基础的比较排序算法，其核心思想是将待排序的序列分为两部分，一部分是已排序的，另一部分是未排序的。在未排序部分选择一个元素，插入到已排序部分的适当位置，以此类推，直到所有元素都被排序完毕。插入排序的实现简单直观，是初学者入门排序算法的绝佳选择。

编程日记2024/01/20 09:06:39

Java数据结构与算法：排序算法之归并排序

归并排序是一种基于分治思想的排序算法，它将待排序的序列划分成若干个子序列，分别进行排序，最后再合并成一个有序的序列。这一过程通过递归实现，直到每个子序列中只有一个元素，即可认为其已经有序。随后，通过两两合并有序序列，最终完成整个序列的排序。

编程日记2024/01/20 09:05:58

Java数据结构与算法：排序算法之选择排序

选择排序是一种基础的比较排序算法，其核心思想是通过多次遍历待排序的元素，每次找到最小（或最大）的元素，放到已排序的序列的末尾（或开头）。尽管选择排序不如一些高级排序算法在性能上优越，但它的思想清晰、实现简单，是学习排序算法的重要一步。

编程日记2024/01/20 09:05:41

Java数据结构与算法：排序算法之冒泡排序

冒泡排序是一种基础的比较排序算法，其核心思想是多次遍历待排序的元素，通过不断交换相邻的元素，使得最大（或最小）的元素逐步移动到正确的位置。虽然它在效率上不如一些高级排序算法，但其实现简单，是学习排序算法的绝佳入门。

编程日记2024/01/20 09:05:16

Java数据结构与算法：排序算法之快速排序

快速排序是一种基于分治思想的排序算法，通过选取一个基准元素，将序列分成两个子序列，分别对左右两个子序列进行排序，从而达到整个序列有序的目的。快速排序的关键在于分区（Partition），即将序列分成两部分，使得左边的元素都小于基准元素，右边的元素都大于基准元素。

编程日记2024/01/20 09:04:38

C# 实现单线程异步互斥锁

C#对异步的支持越来越成熟，async、await简化了代码也提高了可读性，但由于在一段上下文中有了异步操作，意味着这段操作可能会被同时重复调用，如果本身没有被设计可以重复调用的情况下，就很可能会出问题。以上就是今天要讲的内容，本文简单的实现了单线程的异步互斥锁，实现起来相对简单，但作用还是比较大的。虽然说有些情况的异步是可以在前期设计上避免同时调用，比如登录按钮点击后出现蒙板不允许再次点击，但是对于已存在的代码出现了同时调用问题，此时有互斥锁则可以避免大范围改动代码，有效解决问题。_c#实现线程都要经过一个阻塞的方法,线程之间互不干涉

编程日记2024/01/19 21:12:09

【小白专用】C# 连接 MySQL 数据库

C# 连接 MySQL 数据库

编程日记2024/01/17 01:32:11

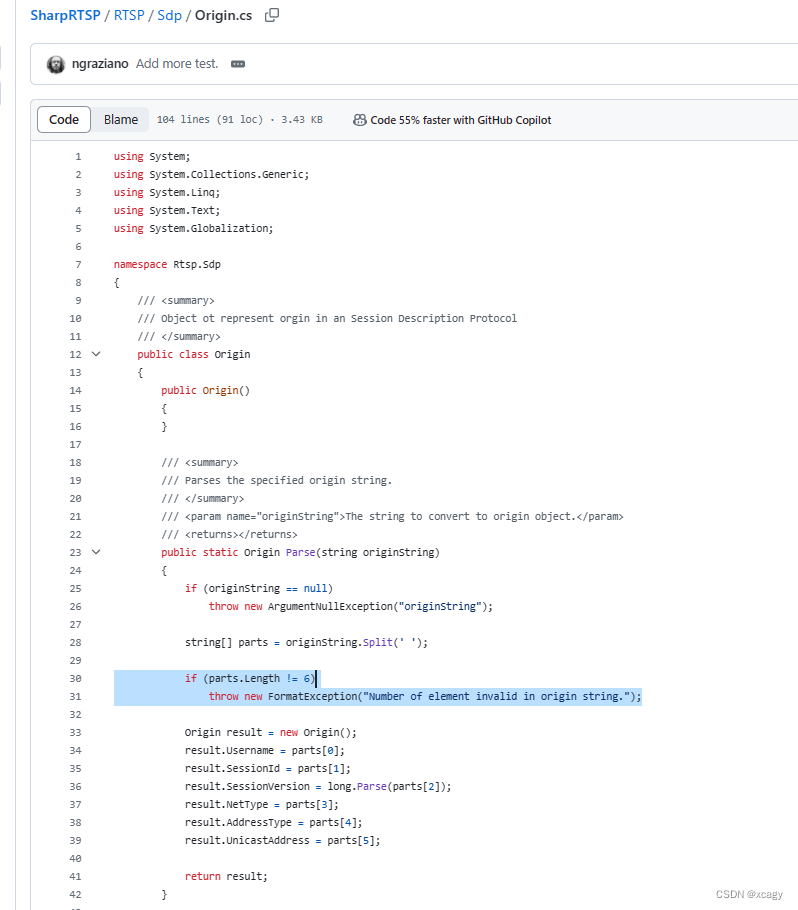
RTSP协议播放不兼容TPLINK摄像头的处理办法

报错的内容是Number of element invalid in origin string.两个数字中间多了一个空格，导致判断数据不等于6。所以数据输入的时候把中间的空格去掉一个即可。

编程日记2024/01/16 16:31:06

Java中 && 和|| 在同一个 if 里面使用会出现啥问题&Java中运算符“|”和“||”以及“&”和“&&”区别

如果在同一个 if 语句中同时使用 && 和 || 运算符，可能会导致逻辑错误。这样就会导致逻辑错误，当 a 为 false，b 为 true 时，输出结果会是 “Goodbye”，而不是我们期望的 “Hello World”。假设有两个布尔类型的变量 a 和 b，我们要判断当 a 为 true 或者 b 为 true 时输出 “Hello World”，否则输出 “Goodbye”。：不论运算符左侧为true还是false，右侧语句都会进行判断，下面代码。

编程日记2024/01/15 22:00:03

【MATLAB】 SSA奇异谱分析信号分解算法

SSA奇异谱分析（Singular Spectrum Analysis）是一种处理非线性时间序列数据的方法，可以对时间序列进行分析和预测。它基于构造在时间序列上的特定矩阵的奇异值分解（SVD），可以从一个时间序列中分解出趋势、振荡分量和噪声。具体流程如下：根据原始时间序列构建轨迹矩阵X XX。对矩阵X进行奇异值分解：X = ∑ i = 1 r σ i U i V i T X=\sum_{i=1}^{r} \sigma_i U_i V_{i}^TX=∑i=1rσiUiViT。

编程日记2024/01/14 21:25:30

ArrayList底层的实现原理

ArrayList底层的实现原理 ArrayList底层是用动态数组实现的 ArrayList初始化容量为0，当第一次添加数据的时候才会初始化为10。 ArrayList在进行扩容的时候是原来容量的1.5倍，每次扩容都需要拷贝数组。 ArrayList在添加数据的时候确保数组已使用长度size+1之后足够存下下一个数据计算数组的容量，如果当前数组已使用长度+1后的大于当前的数组长度，则调用grow方法扩容（原来的1.5倍）确保新增的数据有地方存储之后，则将新

编程日记2024/01/13 10:22:13

C#实现Excel合并单元格数据导入数据集

编程日记2024/01/12 17:30:23

即将消失的五种编程语言？

学习路径困难必然导致非常有限的活跃用户，而 Haskell 的上一个最新的稳定版本是在 2010 年发布，这对于促进它本身的发展无济于事。Perl 于 1987 年开始流行时，它被誉为是适合任何一个人的编程语言，曾经有一段时间，每个人都用Perl编程，但是后来发生了一些事情，开发者开始在不知道原因的情况下添加越来越大的功能，也许这增加了了问题的复杂性。甚至它的作者似乎已经含蓄地解释了Perl的一些问题，并选择停止从2000年开始的Perl 6开发，关键是，似乎现在也没人想要在用Perl。

编程日记2024/01/11 22:56:50

c#调试程序一次启动两个工程（多个工程）

可以在解决方案中设置多个启动项目(右键单击解决方案，转到设置启动项目，选择多个启动项目)，并为包含在解决方案(无开始不调试就开始如果您将多个项目设置为开始，则调试器将在启动时附加到每个项目。

编程日记2024/01/07 13:05:56

C#使用 OpenHardwareMonitor获取CPU或显卡温度、使用率、时钟频率相关方式

代码的功能可以将主板的名称显示出来，还有将第一个CPU的情况显示，可以根据实际情况进行修改。C# 去获取电脑相关的基础信息，还是需要借助外部的库，我这边尝试了自己去实现它。OpenHardwareMonitor获取CPU的温度和频率需要管理员权限。网上有一些信息，但不太完整，都比较零碎，这边尽量将代码完整的去展示出来。引用–>添加引用—>浏览（选择文件）–>确定。代码中注释掉的部分是循环显示的一个循环逻辑。在没有开权限的时候就是无法使用。

编程日记2024/01/03 13:34:35

基于huffman编解码的图像压缩算法matlab仿真

Huffman编码是一种用于无损数据压缩的熵编码算法。由David A. Huffman在1952年提出。该算法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码。

编程日记2023/12/30 16:55:06

python爬虫之selenium模拟浏览器

之前在异步加载（AJAX）网页爬虫的时候提到过，爬取这种ajax技术的网页有两种办法：一种就是通过浏览器审查元素找到包含所需信息网页的真实地址，另一种就是通过selenium模拟浏览器的方法[1]。当时爬的是豆瓣，比较容易分析出所需信息的真实地址，不过一般大点的网站像淘宝这种是不好分析的，所以利用selenium模拟浏览器的行为来爬取数据是一个比较可行的办法。

编程日记2023/12/27 10:10:04

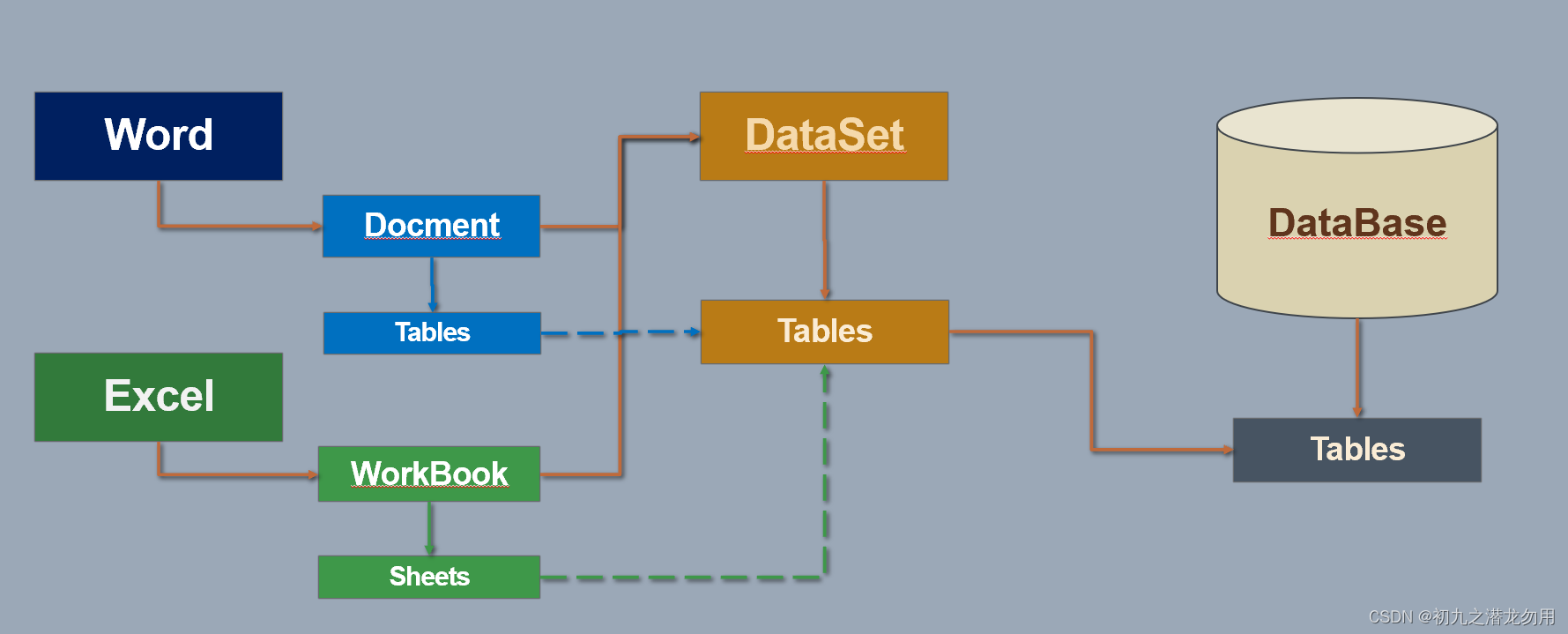
C# 读取Word表格到DataSet

在应用项目里，多数情况下我们会遇到导入 Excel 文件数据到数据库的功能需求，但某些情况下，也存在使用 Word 进行表格数据编辑的情况。Word 和 Excel 其实各有特点，但用户的习惯不同，即使同一数据源，可能提供的数据源文件类型也不同，这其中也包括导入Word内容的功能，比如表格数据导出到DataSet数据集。

编程日记2023/12/25 21:49:20

程序，进程，线程，超线程之间的联系和区别

当我们谈到计算机程序的执行时，经常会涉及到“程序”，“进程”，“线程”和“超线程”这些概念。通过理解这些概念及其之间的联系和区别，可以帮助我们更好地理解计算机程序的执行方式和并发处理机制。来源：6547网 http://www.6547.cn/blog/442。

编程日记2023/12/25 15:39:32

讲解mtrand.RandomState.randint low ＞= high

第一个例子生成了一个介于 0 和 10 之间（不包括 10）的随机整数，而第二个示例生成了一个形状为 (3, 2) 的二维数组，其中的元素是介于 1 和 100 之间（不包括 100）的随机整数。这样，我们就可以在实际的密码重置场景中使用 generate_reset_code() 函数来生成一个随机验证码，并将其发送给用户进行密码重置操作。这段代码的预期目标是生成一个范围为 [low, high) 的随机整数，即在 5 到 3 之间（不包括 3）生成一个整数。的问题，并生成所需范围内的随机整数。

编程日记2023/12/23 20:30:10