【码书】一本经典且内容全面算法书籍,学算法必备

之前推荐了好几本算法书,有《啊哈!算法》,有《算法图解》,有《漫画算法》,也有《我的第一本算法书》,很多粉丝不乐意了,觉得我推荐了这么多算法书籍,竟然没有经典算法书籍《算法导论》,好吧,怪我太年轻,不懂事~请原谅我!

点击封面或者识别下方二维码查看详情

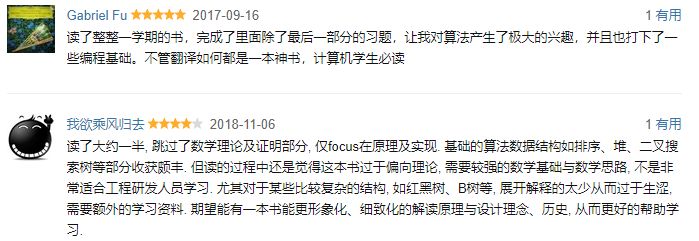
于是我问出版社要来《算法导论》的书摘看看,然后又去网上查了很多的资料,真的没想到《算法导论》这本书的评价那么好,而且书籍里涉及的内容非常的全面,在豆瓣上达到了9.3的高分。

不仅分数高。大家对算法导论的评价也是很高
接下来我们来看一下《算法导论》的书摘
假设计算机是无限快的并且计算机存储器是免费的,你还有什么理由来研究算法吗?即使只是因为你还想证明你的解法会终止并以正确的答案终止,那么回答也是肯定的。
如果计算机无限快,那么用于求解某个问题的任何正确的方法都行。也许你希望你的实现在好的软件工程实践的范围内(例如,你的实现应该具有良好的设计与文档),但是你最常使用的是最容易实现的方法。
当然,计算机也许是快的,但它们不是无限快。存储器也许是廉价的,但不是免费的。所以计算时间是一种有限资源,存储器中的空间也一样。你应该明智地使用这些资源,在时间或空间方面有效的算法将帮助你这样使用资源。
效率
为求解相同问题而设计的不同算法在效率方面常常具有显著的差别。这些差别可能比由于硬件和软件造成的差别要重要得多。
作为一个例子,本书第2章将介绍两个用于排序的算法。第一个称为插入排序,为了排序n个项,该算法所花时间大致等于c1n2,其中c1是一个不依赖于n的常数。也就是说,该算法所花时间大致与n2成正比。第二个称为归并排序,为了排序n个项,该算法所花时间大致等于c2nlgn,其中lgn代表log2n且c2是另一个不依赖于n的常数。与归并排序相比,插入排序通常具有一个较小的常数因子,所以c1<c2。我们将看到就运行时间来说,常数因子可能远没有对输入规模n的依赖性重要。把插入排序的运行时间写成c1n·n并把归并排序的运行时间写成c2n·lgn。这时就运行时间来说,插入排序有一个因子n的地方归并排序有一个因子lgn,后者要小得多。(例如,当n=1000时,lgn大致为10,当n等于100万时,lgn大致仅为20。)虽然对于小的输入规模,插入排序通常比归并排序要快,但是一旦输入规模n变得足够大,归并排序lgn对n的优点将足以补偿常数因子的差别。不管c1比c2小多少,总会存在一个交叉点,超出这个点,归并排序更快。
作为一个具体的例子,我们让运行插入排序的一台较快的计算机(计算机A)与运行归并排序的一台较慢的计算机(计算机B)竞争。每台计算机必须排序一个具有1000万个数的数组。(虽然1000万个数似乎很多,但是,如果这些数是8字节的整数,那么输入将占用大致80MB,即使一台便宜的便携式计算机的存储器也能多次装入这么多数。)假设计算机A每秒执行百亿条指令(快于写本书时的任何单台串行计算机),而计算机B每秒仅执行1000万条指令,结果计算机A就纯计算能力来说比计算机B快1000倍。为使差别更具戏剧性,假设世上最巧妙的程序员为计算机A用机器语言编码插入排序,并且为了排序n个数,结果代码需要2n2条指令。进一步假设仅由一位水平一般的程序员使用某种带有一个低效编译器的高级语言来实现归并排序,结果代码需要50nlgn条指令。为了排序1000万个数,计算机A需要
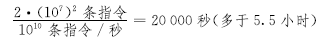
而计算机B需要
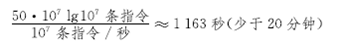
通过使用一个运行时间增长较慢的算法,即使采用一个较差的编译器,计算机B比计算机A还快17倍!当我们排序1亿个数时,归并排序的优势甚至更明显:这时插入排序需要23天多,而归并排序不超过4小时。一般来说,随着问题规模的增大,归并排序的相对优势也会增大。
算法与其他技术
上面的例子表明我们应该像计算机硬件一样把算法看成是一种技术。整个系统的性能不但依赖于选择快速的硬件而且还依赖于选择有效的算法。正如其他计算机技术正在快速推进一样,算法也在快速发展。
你也许想知道相对其他先进的计算机技术(如以下列出的),算法对于当代计算机是否真的那么重要:
先进的计算机体系结构与制造技术
易于使用、直观的图形用户界面(GUI)
面向对象的系统
集成的万维网技术
有线与无线网络的快速组网
回答是肯定的。虽然某些应用在应用层不明确需要算法内容(如某些简单的基于万维网的应用),但是许多应用确实需要算法内容。例如,考虑一种基于万维网的服务,它确定如何从一个位置旅行到另一个位置。其实现依赖于快速的硬件、一个图形用户界面、广域网,还可能依赖于面向对象技术。然而,对某些操作,如寻找路线(可能使用最短路径算法)、描绘地图、插入地址,它还是需要算法。
而且,即使是那些在应用层不需要算法内容的应用也高度依赖于算法。该应用依赖于快速的硬件吗?硬件设计用到算法。该应用依赖于图形用户界面吗?任何图形用户界面的设计都依赖于算法。该应用依赖于网络吗?网络中的路由高度依赖于算法。该应用采用一种不同于机器代码的语言来书写吗?那么它被某个编译器、解释器或汇编器处理过,所有这些都广泛地使用算法。算法是当代计算机中使用的大多数技术的核心。
进一步,随着计算机能力的不断增强,我们使用计算机来求解比以前更大的问题。正如我们在上面对插入排序与归并排序的比较中所看到的,正是在较大问题规模时,算法之间效率的差别才变得特别显著。
是否具有算法知识与技术的坚实基础是区分真正熟练的程序员与初学者的一个特征。使用现代计算技术,如果你对算法懂得不多,你也可以完成一些任务,但是,如果有一个好的算法背景,那么你可以做的事情就多得多。
以上就是《算法导论》的部分书摘啦

如此好的一本算法书籍
原件128元
现在8折优惠哦
购买前还可领券
领券+折扣双重优惠
识别下方二维码领券

然后识别下方二维码或者点击阅读原文购买


作为码书商店的运营人员,诚邀你们进入我们的“CSDN码书福利群”,群里会不定时的给大家赠书书籍、优惠券等,有书籍推荐或者物流方面信息也可群里咨询~目前群已满100人,需要加群的请扫下方二维码添加微信,拉你入群哦~对此次活动不了解的也可咨询~


相关文章:

Ubuntu16.04.1 安装Nginx
Nginx ("engine x") 是一个高性能的 HTTP 和 反向代理 服务器,也是一个 IMAP/POP3/SMTP 代理服务器。 Nginx 是由 Igor Sysoev 为俄罗斯访问量第二的 Rambler.ru 站点开发的,第一个公开版本0.1.0发布于2004年10月4日。其将源代码以类BSD许可证…

linux下jboss的安装配置
闲来无事突然间想到和tomcat相同的java容器jboss,就想测试一下jboss和tomcat性能的差异之处。但是之前只安装过tomcat,想来跟tomcat安装方式应该是相同的都需要jdk的支持。查找资料后进行了安装。一下是我安装jboss的一些步骤:Linux版本&…
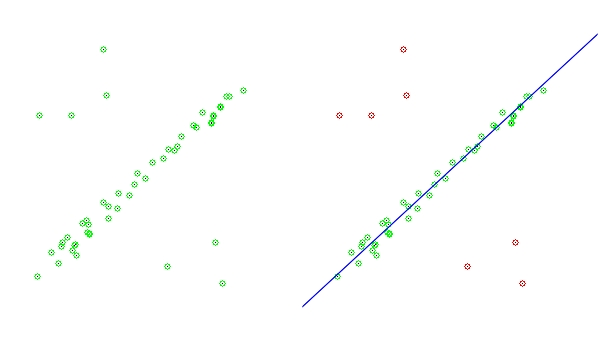
RANSAC鲁棒参数估计
转自:http://blog.csdn.net/zhanglei8893/archive/2010/01/23/5249470.aspx RANSAC 是"RANdom SAmple Consensus"的缩写。该算法是用于从一组观测数据中估计数学模型参数的迭代方法,由Fischler and Bolles在1981 提出,它是一种非确…

AlphaGo之父DeepMind再出神作,PrediNet原理详解
作者 | beyondma转载自CSDN博客近期,DeepMind发表论文,称受Marta Garnelo和 Murray Shanahan的论文“Reconciling deep learning with symbolic artificial intelligence: representing objects and relations”启发,他们提出了一种新的架构…

php中file_get_contents如何读取大容量文件
php中file_get_contents如何读取大容量文件 一、总结 一句话总结:使用file_get_contents()进行分段读取,file_get_contents()函数可以分段读取 1、读取大文件是,file_get_contents()函数为什么会发生错误? 发生内存溢出而打开错误…

Vmware虚拟机的复制后无法使用的问题和解决
为什么80%的码农都做不了架构师?>>> 我在自己的机器上用Vmware安装的Ubuntu 12.04系统,并在里面部署了Openstack的开发环境,部署的过程有些复杂,不希望再次重复这个过程,于是就复制整个的虚拟机文件到其他…

Facebook频谱图模型生成比尔·盖茨声音,性能完胜WaveNet、MAESTRO
作者 | James Vincent 等编译 | 夕颜、Monanfei出品 | AI科技大本营(ID:rgznai100)计算机生成语音领域,正在酝酿着和一场革命。Facebook 工程师们设计创建的机器学习模型 MelNet 就是一个启示。下面这段听起来怪异的话像极了比尔盖茨是吧&…

数据表设计的原则
如何设计数据表: 三个范式 ER图

图像配准----Harris算子
Harris算子是C.Harris和M.J.Stephens在1988年提出的一种特征点提取算子。它用一阶偏导来描述亮度变化,这种算子受信号处理中自相关函数的启发,给出与自相关函数相联系的矩阵M。M矩阵的特征值是自相关函数的一阶曲率,如果两个曲率值都高&#…

关于ORA-01950: no privileges on tablespace 的解决
前天晚上,本想在家里搭一个公司项目的开发环境,以便在工作忙的时候做点“家庭作业”。下班之前,通过PLSQL Developer导数据库时,不知道什么原因,以.dmp格式导出时总不成功,于是选择以.sql格式导出ÿ…

继往开来!目标检测二十年技术综述
作者 | 周强来源 | 我爱计算机视觉(id:aicvml)计算机视觉中的目标检测,因其在真实世界的大量应用需求,比如自动驾驶、视频监控、机器人视觉等,而被研究学者广泛关注。几天前,arXiv新出一篇目标检…

python+selenium百度贴吧自动签到
#-*- coding:utf-8 -*- from selenium import webdriver import time import os import random from selenium.webdriver.common.action_chains import ActionChainsbrowser webdriver.Chrome()# 最大等待加载完的时间 max_loading 600 # 延时随机n秒执行 wait_time random.…

图像配准----NCC
在用Harris算子对图像进行角点提取后,两幅图像得到的角点个数不一定相等,这时就要先对它们进行处理,得出一一对应的角点对。 归一化互相关(Normalized Cross Correlation method, NCC)匹配算法是一种经典的统计匹配算法,通过计算模…

Ext Scheduler Web资源甘特图控件
原文来自 http://www.fanganwang.com/Product-detail-item-1430.html欢迎转载。 关键字: 资源甘特图又叫负荷图,其纵轴不再列出活动,而是列出整个部门或特定的资源。 Ext Scheduler资源甘特图是基于Extjs核心库的开发的,基于WEB浏…

50行代码教AI实现动作平衡 | 附完整代码
作者 | Mike Shi译者 | linstancy责编 | Jane出品 | AI科技大本营(id:rgznai100)【导读】本文将为大家展示如何通过 Numpy 库和 50行 Python 代码,使用标准的 OpenAI Gym平台创建智能体 (agent),就教会机器处理推车杆问…

图像配准----双向匹配
由Harris提取出的两幅图像的角点个数或对应关系并不是一一对应的。为了后续的配准,需要先对提取出的角点进行初始匹配,双向匹配方法是比较简单的一种方法,它实现容易。 设参考图像特征点集为X {x1, x2, …,xp}, p > 3;待配准图…
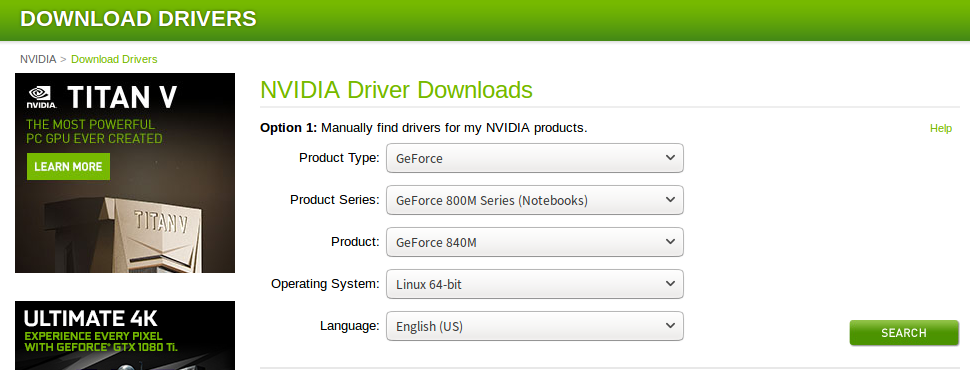
[专业亲测]Ubuntu16.04安装Nvidia显卡驱动(cuda)--解决你的所有困惑【转】
本文转载自: 因为要做毕设需要安装caffe2,配置cuda8.0,但是安装nvidia驱动真的是把我难倒了,看了很多篇博文都没有效果,现在我自己重新总结了下几种 安装方法(亲测有效),希望能帮到大…

IE下javascript的console方法
IE下javascript的console方法 FireFox 和 Chrome 下调试JS都有console,IE6下没有。特用此办法来兼容IE6. <br /><pre lang‘‘html‘‘> <!doctype html> <html> <head> <meta charset‘‘utf-8‘‘/> </head> <body&…

图像配准----RANSAC
对角点进行初始匹配后,所选定的角点并不能保证全部是正确的点,也可能有误点,因此,还需要进一步对所选定的角点进行精确匹配。 RANSAC(RANdom Sample And Consensus)方法是由Fischler和Bolles提出的一种鲁棒性的参数估计方法。它的…

教你用OpenCV实现机器学习最简单的k-NN算法
前言:OpenCV 的构建是为了提供计算机视觉的通用基础接口,现在已经成为经典和最优秀的计算机视觉和机器学习的综合算法工具集。作为一个开源项目,研究者、商业用户和政府部门都可以轻松利用和修改现成的代码。k-NN算法可以认为是最简单的机器学…

div 相同属性提取
把样式名或id写在一起,用逗号隔开 <!DOCTYPE html><html lang"en"><head> <meta charset"UTF-8"> <title>信息详情</title> <style type"text/css"> #box-1, #box-2, #box…
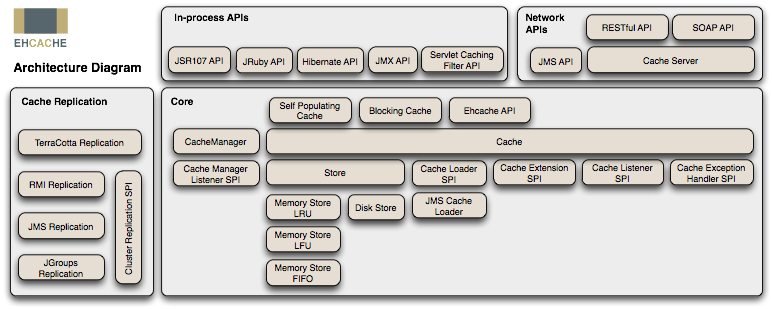
ehcache 简介
hCache 是一个纯Java的进程内缓存框架,具有快速、精干等特点,是Hibernate中默认的CacheProvider。 下图是 Ehcache 在应用程序中的位置: ehcache部署起来很简单,主要分两步: 1.首先要给他写个核心配置XML文件 <ehca…
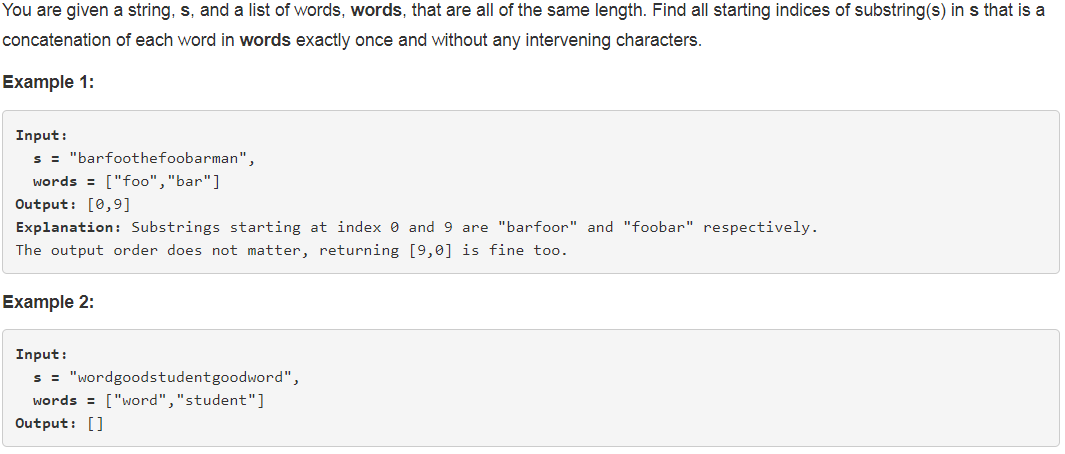
【leetcode】30. Substring with Concatenation of All Words
题目如下: 解题思路:本题题干中有一个非常关键的前提,就是words中的所有word的长度一样,并且都要被使用到。所以,我们可以把输入的s按word的长度进行等分,以s "barfoothefoobarman",words [&qu…

图像配准----SIFT
SIFT算子(Scale Invariant Feature Transform)是David Lowe提出的一种基于尺度空间的、对图像缩放、旋转甚至仿射变换保持不变性的图像局部特征描述算子。SIFT特征提取的是极其细微、大量的特征点,即时少数物体、物体的一小部分也可以产生大量特征向量。 SIFT算法如…

终于把微软BING搜索-SPTAG算法的原理搞清了
作者 | beyondma转载自 CSDN 博客近日,微软在GitHub上开源了其BING的搜索算法SPTAG,github地址:https://github.com/microsoft/SPTAG。这个算法笔者简单看了一下,的确是很有价值可以看大家介绍下,这种称为SPTAG &#…

把握每天的第一个钟头
当我十七岁的时候,我读到一段话,它是这么说的:“如果你把每天都当做最后一天来活着,那么有一天你将会是对的。”这句话让我留下了深刻的印象,从那时候开始,过去的 33 年来,我每天早上都对着镜子…

向量叉积计算法
如果向量A为{a, b, c},向量B为{m, n, p},如何计算向量A与向量B的叉积呢? 用行列式: |i j k| |a b c| |m n p| (bp-cn)i (mc-pa)j (an-bm)k 例如用matlab实现两个向量的叉积: a [1 2 3]; …

你是个成熟的C位检测器了,应该可以自动找C位了
作者 | 李翔转载自视说AI(ID:techtalkai)写在前面C位是近年网络上一个比较热门的词,最早来源于DOTA等游戏领域,是核心位置(Carry位)的简称,代表的是能够在游戏前中期打钱发育并在游戏后期带领队…
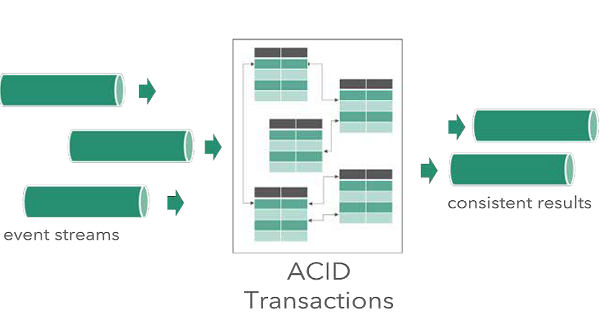
Data Artisans发布支持ACID事务的流式处理框架Streaming Ledger
data Artisans宣布推出Streaming Ledger,它扩展了Apache Flink,提供了跨表、键和事件流执行可序列化ACID事务的功能。这项正在申请专利的技术是Flink的专有附加技术,超越了当前一次只能在一个键上实现一致性的标准。\\在发布Streaming Ledger…

The Life Cycle of a Servlet
为什么80%的码农都做不了架构师?>>> Servlet的生命周期由Servlet容器管理,包含如下几个步骤: 1. 装载Servlet类; 2. 创建Servlet的实例; 3. 调用Servlet的init()方法; 4. 调用Servlet的service()方法; 5. 调用Servlet的destroy()…
