一文读懂线性回归、岭回归和Lasso回归

(图片由AI科技大本营付费下载自视觉中国)
作者 | 文杰
编辑 | yuquanle
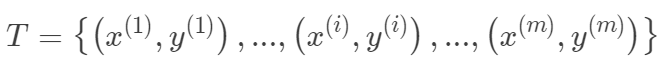
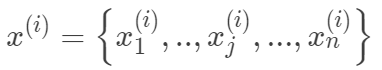 ,
,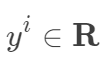 。其中m为训练集样本数,n为样本维度,y是样本的真实值。线性回归采用一个高维的线性函数来尽可能的拟合所有的数据点,最简单的想法就是最小化函数值与真实值误差的平方(概率解释-高斯分布加最大似然估计)。即有如下目标函数:
。其中m为训练集样本数,n为样本维度,y是样本的真实值。线性回归采用一个高维的线性函数来尽可能的拟合所有的数据点,最简单的想法就是最小化函数值与真实值误差的平方(概率解释-高斯分布加最大似然估计)。即有如下目标函数: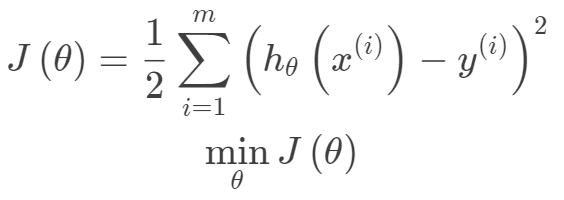
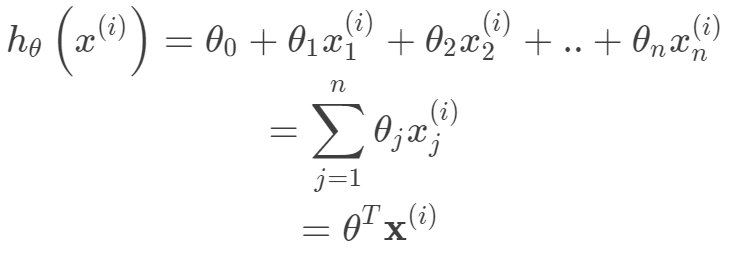
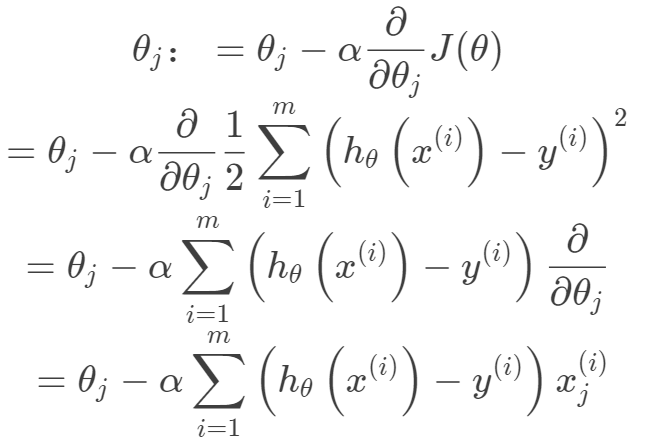
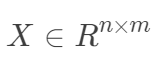 ,
,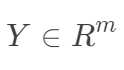 ,构成如下数据矩阵。
,构成如下数据矩阵。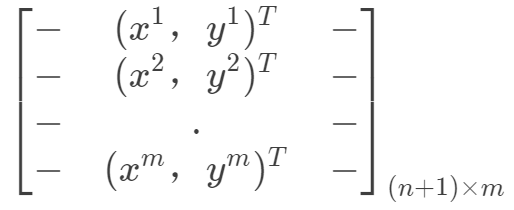
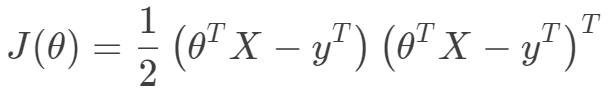
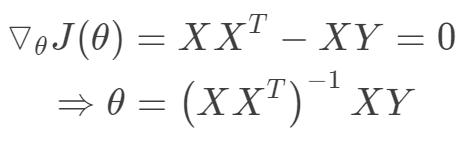
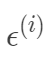 ,那么预测值
,那么预测值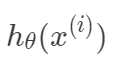 与真实值
与真实值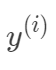 之间有如下关系:
之间有如下关系: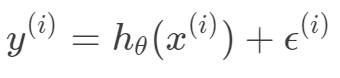
根据中心极限定理,当一个事件与很多独立随机变量有关,该事件服从正态分布 。一般来说,连续值我们都倾向于假设服从正态分布。假设每个样本的误差
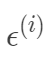 独立同分布均值为0,方差为σ的高斯分布
独立同分布均值为0,方差为σ的高斯分布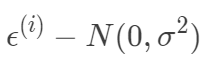 ,所以有:
,所以有: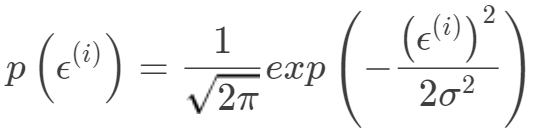
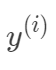 满足以均值为
满足以均值为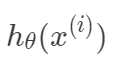 ,方差为
,方差为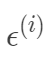 的高斯分布。
的高斯分布。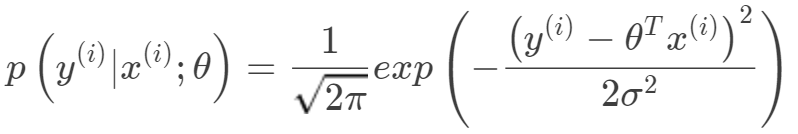
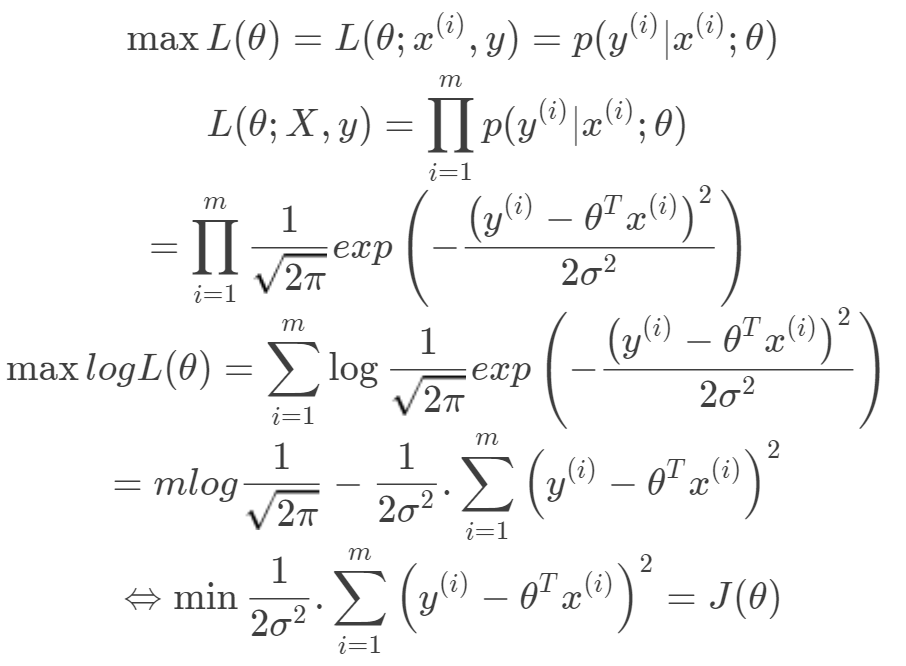
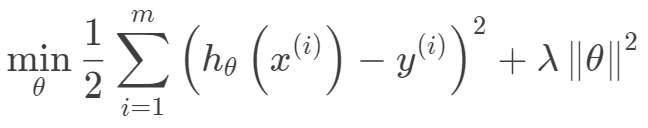
其迭代优化函数如下:
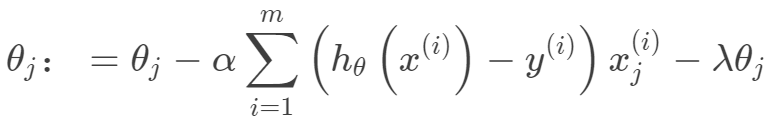
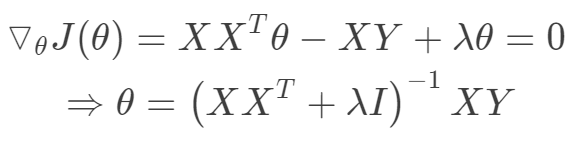
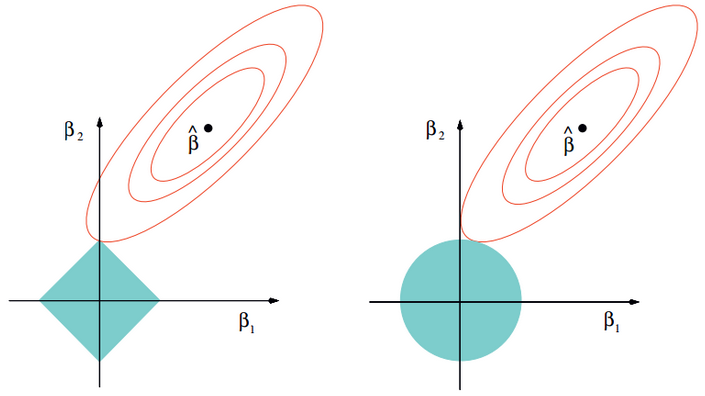
Lasso回归采用一范数来约束,使参数非零个数最少。而Lasso和岭回归的区别很好理解,在优化过程中,最优解为函数等值线与约束空间的交集,正则项可以看作是约束空间。可以看出二范的约束空间是一个球形,而一范的约束空间是一个方形,这也就是二范会得到很多参数接近0的值,而一范则尽可能非零参数最少。
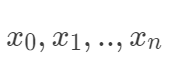 的坐标上是线性的,但是并不表示线性的模型就一定只能用于线性分布问题上。假如我们只有一个特征
的坐标上是线性的,但是并不表示线性的模型就一定只能用于线性分布问题上。假如我们只有一个特征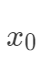 ,而实际上回归值是
,而实际上回归值是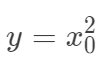 等,我们同样可以采用线性模型,因为我们完全可以把输入空间映射到高维空间
等,我们同样可以采用线性模型,因为我们完全可以把输入空间映射到高维空间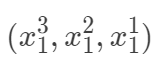 ,其实这也是核方法以及PCA空间变换的一种思想,凡是对输入空间进行线性,非线性的变换,都是把输入空间映射到特征空间的思想,所以只需要把非线性问题转化为线性问题即可。另外一种是局部线性思想,即对每一个样本构建一个加权的线性模型。
,其实这也是核方法以及PCA空间变换的一种思想,凡是对输入空间进行线性,非线性的变换,都是把输入空间映射到特征空间的思想,所以只需要把非线性问题转化为线性问题即可。另外一种是局部线性思想,即对每一个样本构建一个加权的线性模型。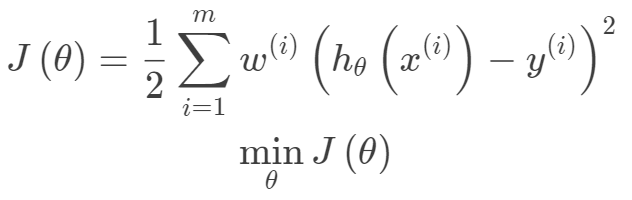
一般选择下面的权重函数,权重函数选择并非因为其类似于高斯函数,而是根据数据分布的特性,但权重函数的选取并不一定依赖于数据特性。
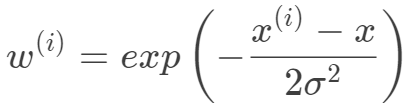
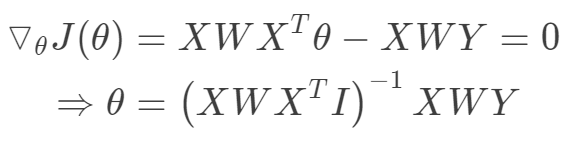
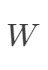 是对角矩阵,
是对角矩阵, 。
。/**
线性回归函数的实现,考虑一般的线性回归,最小平方和作为损失函数,则目标函数是一个无约束的凸二次规划问题,
由凸二次规划问题的极小值在导数为0处取到,且极小值为全局最小值,且有闭式解。根据数学表达式实现矩阵之间的运算求得参数w。
**/
int regression(Matrix x,Matrix y)
{
Matrix xT=x.transposeMatrix();
Matrix xTx=xTx.multsMatrix(xT,x);
Matrix xTx_1=xTx.niMatrix();
Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT);
Matrix ws;
ws=ws.multsMatrix(xTx_1xT,y);
cout<<"ws"<<endl;
ws.print();
return 0;
}
/**
下面的岭回归函数只是在一般的线性回归函数的基础上在对角线上引入了岭的概念,不仅有解决矩阵不可逆的线性,同样也有正则项的目的,
采用常用的二范数就得到了直接引入lam的形式。
**/
int ridgeRegres(Matrix x,Matrix y,double lam)
{
Matrix xT=x.transposeMatrix();
Matrix xTx=xTx.multsMatrix(xT,x);
Matrix denom(xTx.row,xTx.col,lam,"diag");
xTx=xTx.addMatrix(xTx,denom);
Matrix xTx_1=xTx.niMatrix();
Matrix xTx_1xT=xTx_1xT.multsMatrix(xTx_1,xT);
Matrix ws=ws.multsMatrix(xTx_1xT,y);
cout<<"ws"<<endl;
ws.print();
return 0;
}
/**
局部加权线性回归是在线性回归的基础上对每一个测试样本(训练的时候就是每一个训练样本)在其已有的样本进行一个加权拟合,
权重的确定可以通过一个核来计算,常用的有高斯核(离测试样本越近,权重越大,反之越小),这样对每一个测试样本就得到了不一样的
权重向量,所以最后得出的拟合曲线不再是线性的了,这样就增加的模型的复杂度来更好的拟合非线性数据。
**/
//需要注意的是局部加权线性回归是对每一个样本进行权重计算,所以对于每一个样本都有一个权重w,所以下面的函数只是局部线性回归的一个主要辅助函数
Matrix locWeightLineReg(Matrix test,Matrix x,Matrix y,const double &k)
{
Matrix w(x.row,x.row,0,"T");
double temp=0;
int i,j;
/**
根据测试样本点与整个样本的距离已经选择的核确定局部加权矩阵,采用对角线上为局部加权值
**/
for(i=0;i<x.row;i++)
{
temp=0;
for(j=0;j<x.col;j++)
{
temp+=(test.data[0][j]-x.data[i][j])*(test.data[0][j]-x.data[i][j]);
}
w.data[i][i]=exp(temp/-2.0*k*k);
}
Matrix xT=x.transposeMatrix();
Matrix wx=wx.multsMatrix(w,x);
Matrix xTwx;
xTwx=xTwx.multsMatrix(xT,wx);
Matrix xTwx_1;
xTwx_1=xTwx.niMatrix();
Matrix xTwx_1xT;
xTwx_1xT=xTwx_1xT.multsMatrix(xTwx_1,xT);
Matrix xTwx_1xTw;
xTwx_1xTw=xTwx_1xTw.multsMatrix(xTwx_1xT,w);
Matrix ws = xTwx_1xTw * y;
return ws;
}
◆
精彩推荐
◆

推荐阅读
100多次竞赛后,他研发了一个几乎可以解决所有机器学习问题的框架
王霸之路:从0.1到2.0,一文看尽TensorFlow“奋斗史”
伯克利人工智能研究院开源深度学习数据压缩方法Bit-Swap,性能创新高
NLP被英语统治?打破成见,英语不应是「自然语言」同义词
TensorFlow2.0正式版发布,极简安装TF2.0(CPU&GPU)教程
肖仰华:知识图谱构建的三要素、三原则和九大策略 | AI ProCon 2019
AI落地遭“卡脖子”困境:为什么说联邦学习是解决良方?
10分钟搭建你的第一个图像识别模型 | 附完整代码
限时早鸟票 | 2019 中国大数据技术大会(BDTC)超豪华盛宴抢先看!

你点的每个“在看”,我都认真当成了喜欢
相关文章:

tf.matmul / tf.multiply
import tensorflow as tfimport numpy as np 1.tf.placeholder placeholder()函数是在神经网络构建graph的时候在模型中的占位,此时并没有把要输入的数据传入模型,它只会分配必要的内存。 等建立session,在会话中,运行模型的时候通…

Java 匿名类也能使用构造函数
为什么80%的码农都做不了架构师?>>> 匿名类虽然没有名字,但可以有一个初始化块来充当构造函数。 public enum Ops {ADD, SUB} public class Calculator { private int i, j, result; public Calculator() {} public Calculator(int _i, …

CUDA Samples: matrix multiplication(C = A * B)
以下CUDA sample是分别用C和CUDA实现的两矩阵相乘运算code即C A*B,CUDA中包含了两种核函数的实现方法,第一种方法来自于CUDA Samples\v8.0\0_Simple\matrixMul,第二种采用普通的方法实现,第一种方法较快,但有些复杂&am…

业界首个实时多目标跟踪系统开源
(图片由AI科技大本营付费下载自视觉中国)作者 | CV君来源 | 我爱计算机视觉(ID:aicvml)相对业界研究比较多的单目标跟踪,多目标跟踪(Multi-Object Tracking,MOT)系统在实…

python基础 练习题
【练习题1】实现一个整数加法计算器如 content input(">>> ") # 59 , 64 count0 while 1:contentinput(>>>)s1 content.split()print(s1)count 0for i in s1:count int(i)print(count) 【练习题2】请编写1 - 100 所有数的和 sum0 for i in r…

[再寄小读者之数学篇](2014-04-18 from 352558840@qq.com [南开大学 2014 年高等代数考研试题]二次型的零点)...
(2014-04-18 from 352558840qq.com [南开大学 2014 年高等代数考研试题]) 设 ${\bf A}$ 为实对称矩阵, 存在线性无关的向量 ${\bf x}_1,{\bf x}_2$, 使得 ${\bf x}_1^T{\bf A}{\bf x}_1>0$, ${\bf x}_2^T{\bf A}{\bf x}_2<0$. 证明: 存在线性无关的向量 ${\bf x}_3,{\bf …

从0到1详解推荐系统中的嵌入方法,原理、算法到应用都讲明白了
(图片由AI科技大本营付费下载自视觉中国)作者丨gongyouliu编辑丨lily来源 | 大数据与人工智能(ID:)前言作者曾在这篇文章中提到,矩阵分解算法是一类嵌入方法,通过将用户行为矩阵分解为用户特征矩…

iOS-Swift中的递增(++)和递减(--)被取消的原因-官方答复
众所周知,在很多编程语言中,对一个变量递增1用,递减1用--,在Swift3之前也是可以这么用的,但之后被取消了。 所以在目前Swift5的版本中,只能用1和-1来进行递增和递减了 如果坚持用或--将会提示以下错误&…
CUDA Samples: 获取设备属性信息
通过调用CUDA的cudaGetDeviceProperties函数可以获得指定设备的相关信息,此函数会根据GPU显卡和CUDA版本的不同得到的结果也有所差异,下面code列出了经常用到的设备信息:#include "funset.hpp" #include <iostream> #include…

apache代理模块proxy使用
1、安装proxy模块[rootlocalhost modules]# cd /usr/local/src/httpd-2.2.16 [rootlocalhost httpd-2.2.16]# cd modules [rootlocalhost modules]# ls aaa config5.m4 debug filters ldap Makefile.in NWGNUmakefile ssl arch database echo …

CUDA Samples: image normalize(mean/standard deviation)
以下CUDA sample是分别用C和CUDA实现的通过均值和标准差对图像进行类似归一化的操作,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:关于均值和标准差的计算公式可参考: http://blog.csdn.net/fengbingchun/article/detai…

中文预训练ALBERT模型来了:小模型登顶GLUE,Base版模型小10倍、速度快1倍
(图片由AI科技大本营付费下载自视觉中国)作者 | 徐亮(实在智能算法专家) 来源 | AINLP(ID:nlpjob)谷歌ALBERT论文刚刚出炉一周,中文预训练ALBERT模型来了,感兴趣的同学可以直接尝鲜试…

树莓派安装go
简介 大学的时候在使用openfalcon的时候讲过这个东西,但是那时候是介绍open-falcon的,所以感觉不是很具体,所以今天在安装frp的时候也碰到了这个问题,我就具体的说下 安装go1.4 编译最新版本的go的时候一定要先编译安装go1.4&…

设计模式中的原则
设计模式(详情click)这个术语是由Erich Gamma等人在1990年代从建筑设计领域引入到计算机科学的。它是对软件设计中普遍存在(反复出现)的各种问题,所提出的解决方案。 设计模式并不直接用来完成代码的编写,而是描述在各种不同情况下…

CUDA Samples: approximate image reverse
以下CUDA sample是分别用C和CUDA实现的对图像进行某种类似reverse的操作,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:common.hpp:#ifndef FBC_CUDA_TEST_COMMON_HPP_ #define FBC_CUDA_TEST_COMMON_HPP_#include<random> #i…

超详细支持向量机知识点,面试官会问的都在这里了
(图片付费下载自视觉中国)作者 | 韦伟来源 | 知乎导语:持续准备面试中,准备的过程中,慢慢发现,如果死记硬背的话很难,可当推导一遍并且细细研究里面的缘由的话,面试起来应该什么都不…

vue-router点击切换路由报错
报错: 报错原因: 设置mode:history解决方法: 将router的mode设置为‘hash就不报错了 原因下次再分析?

gvim配置相关
用 vundle 来管理 vim 插件(包含配置文件vimrc和gvimrc) gvim插件管理神器:vundle的安装与使用 Vim插件管理Vundle Linux 下VIM的配置 Vim配置系列(一) ---- 插件管理 Vim配置系列(二) —- 好看的statusline vim优秀插件整理 一些有用的 VIM …

深度学习有哪些接地气又好玩的应用?
过去几年中,深度学习中的很多技术如计算机视觉、自然语言处理等被应用在很多实际问题中,而且相关成果也表明深度学习能让人们的工作效果比以前更好。我们收集了一些深度学习方面的创意应用,虽然没有对每项应用进行详尽描述,但是希…

Ubuntu下通过CMake文件编译CUDA+OpenCV代码操作步骤
在 CUDA_Test 工程中,CUDA测试代码之前仅支持在Windows10 VS2013编译,今天在Ubuntu 14.04下写了一个CMakeLists.txt文件,支持在Linux下也可以通过CMake编译CUDA_Test工程,CMakeLists.txt文件内容如下:# CMake file f…

JAVA 多用户商城系统b2b2c-Spring Cloud常见问题与总结(一)
在使用Spring Cloud的过程中,难免会遇到一些问题。所以对Spring Cloud的常用问题做一些总结。需要JAVA Spring Cloud大型企业分布式微服务云构建的B2B2C电子商务平台源码 一零三八七七四六二六 一、Eureka常见问题 1.1 Eureka 注册服务慢 默认情况下,服务…
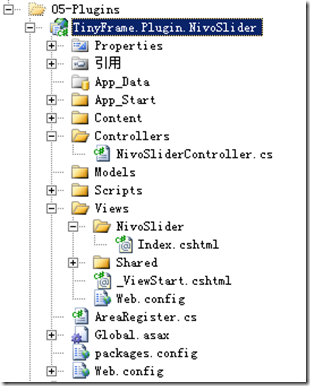
TinyFrame升级之八:实现简易插件化开发
本章主要讲解如何为框架新增插件化开发功能。 在.net 4.0中,我们可以在Application开始之前,通过PreApplicationStartMethod方法加载所需要的任何东西。那么今天我们主要做的工作就集中在这个时间段: 1.将插件DLL及文件拷贝入主网站目录并编译…
快手王华彦:端上视觉技术的极致效率及其短视频应用实践 | AI ProCon 2019
演讲嘉宾 | 王华彦(快手硅谷Y-tech实验室负责人) 编辑 | Just 出品 | AI科技大本营(ID:rgznai100) 快手用户日均上传1500万个视频,要把这些作品准确的分发给超2亿活跃用户,如果没有强大的AI技术系统去理解…
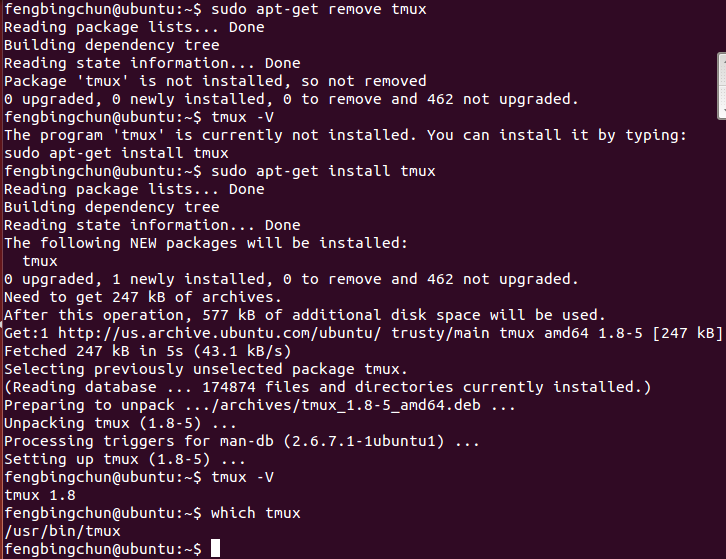
tmux简介及安装
tmux是一个开源工具,用于在一个终端窗口中运行多个终端会话。它可以减少过多的打开终端控制台。tmux的源码在 https://github.com/tmux/tmux ,它的License是BSD。tmux可以直接通过sudo apt-get install tmux命令安装(通过sudo apt-get remove tmux移除)…

Swift中依赖注入的解耦策略
原文地址:Dependency Injection Strategies in Swift 简书地址:Swift中依赖注入的解耦策略 今天我们将深入研究Swift中的依赖注入,这是软件开发中最重要的技术之一,也是许多编程语言中使用频繁的概念。 具体来说,我们将…

Eclipse mac 下的快捷键
2019独角兽企业重金招聘Python工程师标准>>> Eclipse,MyEclipse 的preference 在“windows”下边,mac下在左上角苹果图标边上 win下我们都习惯了ctrl c,在Mac 下使用标准键盘变成了win键c 系统的偏好设定 -> 键盘 -> 修饰…
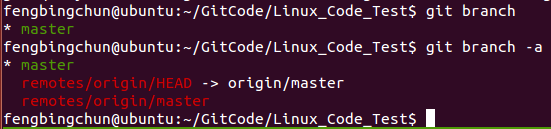
Ubuntu上使终端显示Git分支(oh-my-zsh)
oh-my-zsh是基于Zsh(Zsh是一个Linux用户很少使用的power-shell,这是由于大多数Linux产品安装,以及默认使用bash shell)的功能作了一个扩展,方便插件管理、主体自定义等。oh-my-zsh源码在 https://github.com/robbyrussell/oh-my-zsh &#x…

天哪!我的十一假期被AI操控了
(图片付费下载自视觉中国)导语:这个假期,除了脑海一直在唱歌,庆祝祖国成立的 70 周年,当然也闲不住,要乘机出去浪一浪。目前小长假进度条已经进行到 71.4% 了,有没有发现这个假期与以…
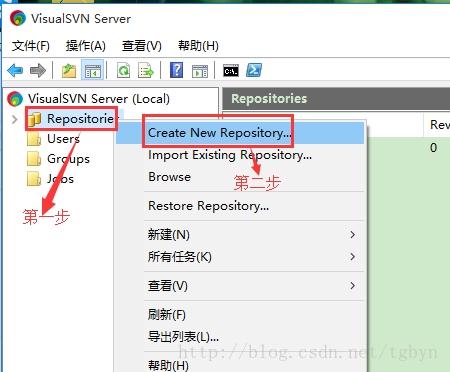
使用SVN+Axure RP 8.0创建团队项目
一、使用到的工具:VisualSVN Server --SVN服务器:https://www.visualsvn.com/server/ Axure RP 8.0 :http://www.downcc.com/soft/103078.html 二、VisualSVN Server 安装以及操作1、安装 : 默认安装即可 2、操作: &a…

no no no.不要使用kill -9.
2019独角兽企业重金招聘Python工程师标准>>> no no no.不要使用kill -9. 它没有给进程留下善后的机会: 1) 关闭socket链接 2) 清理临时文件 3) 将自己将要被销毁的消息通知给子进程 4) 重置自己的终止状态 等等。 通常,应该发送15,…
