超详细支持向量机知识点,面试官会问的都在这里了

(图片付费下载自视觉中国)
作者 | 韦伟
来源 | 知乎
- 当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机;
- 当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;
- 当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。

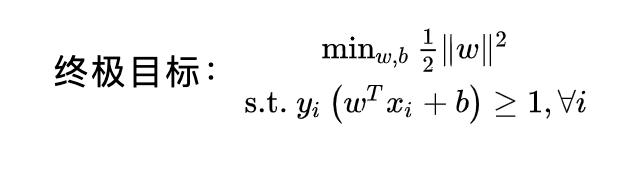
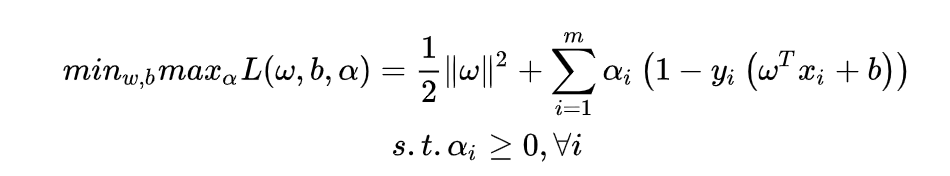
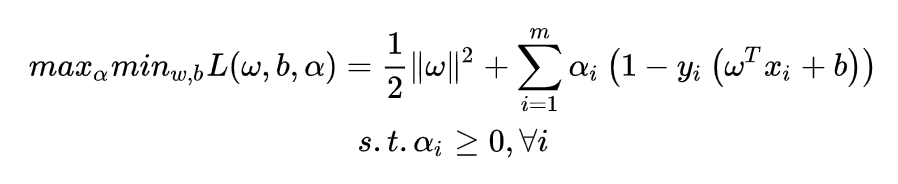
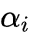 和
和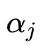 ,选取的两个变量所对应的样本之间间隔要尽可能大,因为这样更新会带给目标函数值更大的变化。SMO算法之所以高效,是因为仅优化两个参数的过程实际上仅有一个约束条件,其中一个可由另一个表示,这样的二次规划问题具有闭式解。
,选取的两个变量所对应的样本之间间隔要尽可能大,因为这样更新会带给目标函数值更大的变化。SMO算法之所以高效,是因为仅优化两个参数的过程实际上仅有一个约束条件,其中一个可由另一个表示,这样的二次规划问题具有闭式解。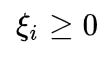 ,公式变为:
,公式变为: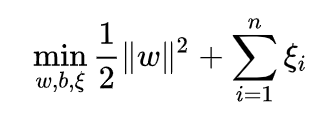
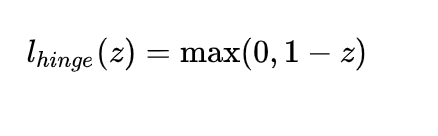
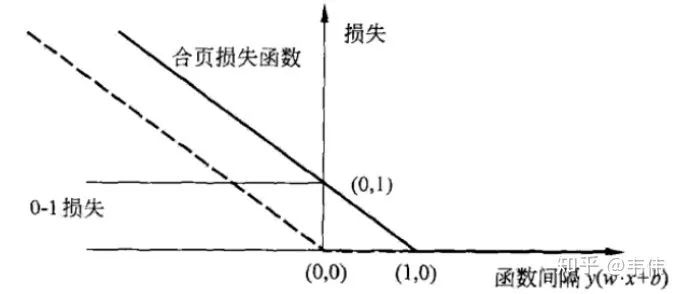
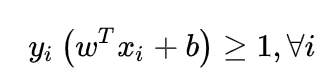 ,现在出现错误的时候,一定是这个式子不被满足了,即
,现在出现错误的时候,一定是这个式子不被满足了,即 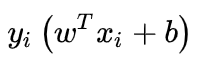 来衡量错误了多少,所以目标变为(正确分类的话损失为0,错误的话付出代价):
来衡量错误了多少,所以目标变为(正确分类的话损失为0,错误的话付出代价):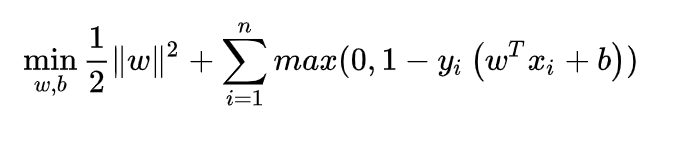
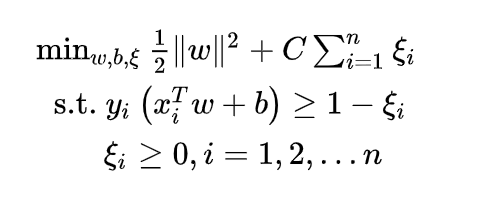
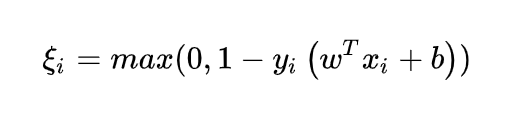
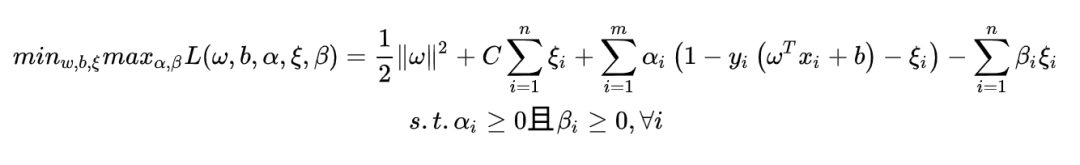
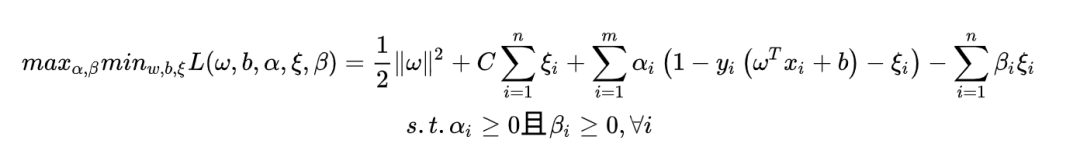
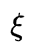 求偏导并令其等于0可得:
求偏导并令其等于0可得: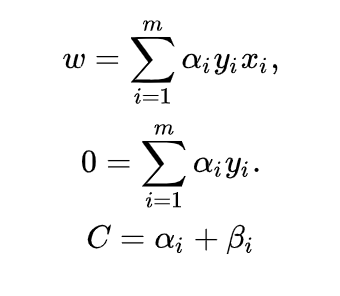
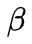 被消掉了:
被消掉了: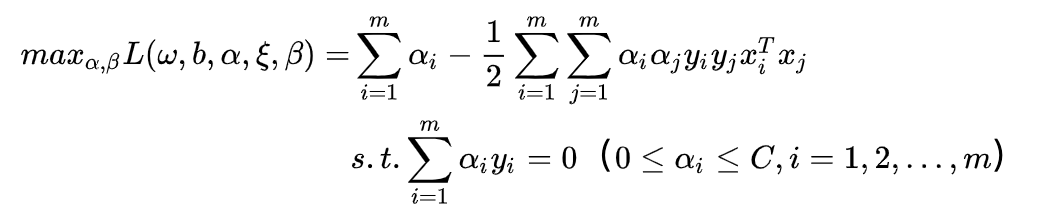
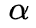 ,同样利用SMO(序列最小优化)算法。
,同样利用SMO(序列最小优化)算法。


- 当特征维数 d 超过样本数 m 时 (文本分类问题通常是这种情况), 使用线性核;
- 当特征维数 d 比较小. 样本数 m 中等时, 使用RBF核;
- 当特征维数 d 比较小. 样本数 m 特别大时, 支持向量机性能通常不如深度神经网络。

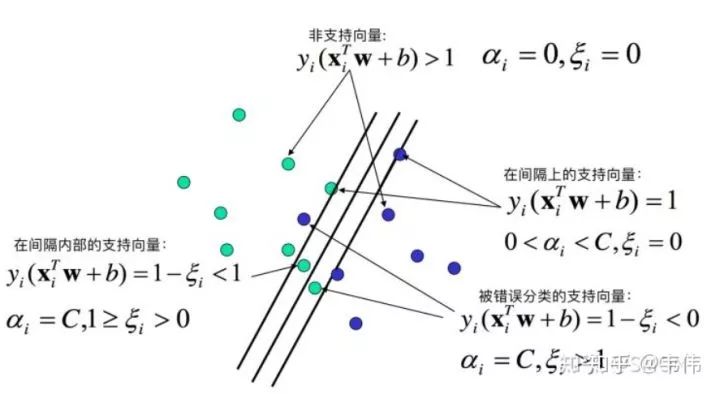
- 线性支持向量机中, 支持向量是距离划分超平面最近的样本, 落在最大间隔边界上。

- 支持向量机的参数 (w; b) 仅由支持向量决定, 与其他样本无关。


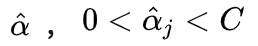 。
。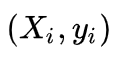 ,
,

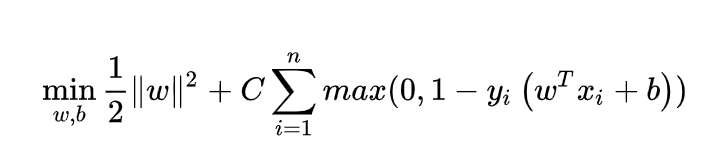
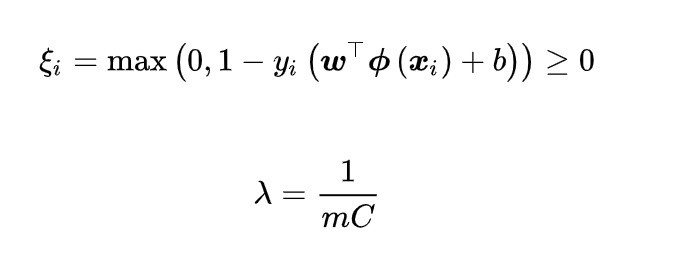
- 由于SVM是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优。
- 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
- 拥有高维样本空间的数据也能用SVM,这是因为数据集的复杂度只取决于支持向量而不是数据集的维度,这在某种意义上避免了“维数灾难”。
- 理论基础比较完善(例如神经网络就更像一个黑盒子)。
- 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)
- 只适用于二分类问题。(SVM的推广SVR也适用于回归问题;可以通过多个SVM的组合来解决多分类问题)
◆
精彩推荐
◆

推荐阅读
中文预训练ALBERT模型来了:小模型登顶GLUE,Base版模型小10倍、速度快1倍
100多次竞赛后,他研发了一个几乎可以解决所有机器学习问题的框架
王霸之路:从0.1到2.0,一文看尽TensorFlow“奋斗史”
伯克利人工智能研究院开源深度学习数据压缩方法Bit-Swap,性能创新高
NLP被英语统治?打破成见,英语不应是「自然语言」同义词
TensorFlow2.0正式版发布,极简安装TF2.0(CPU&GPU)教程
肖仰华:知识图谱构建的三要素、三原则和九大策略 | AI ProCon 2019
AI落地遭“卡脖子”困境:为什么说联邦学习是解决良方?
限时早鸟票 | 2019 中国大数据技术大会(BDTC)超豪华盛宴抢先看!

你点的每个“在看”,我都认真当成了喜欢
相关文章:

vue-router点击切换路由报错
报错: 报错原因: 设置mode:history解决方法: 将router的mode设置为‘hash就不报错了 原因下次再分析?

gvim配置相关
用 vundle 来管理 vim 插件(包含配置文件vimrc和gvimrc) gvim插件管理神器:vundle的安装与使用 Vim插件管理Vundle Linux 下VIM的配置 Vim配置系列(一) ---- 插件管理 Vim配置系列(二) —- 好看的statusline vim优秀插件整理 一些有用的 VIM …

深度学习有哪些接地气又好玩的应用?
过去几年中,深度学习中的很多技术如计算机视觉、自然语言处理等被应用在很多实际问题中,而且相关成果也表明深度学习能让人们的工作效果比以前更好。我们收集了一些深度学习方面的创意应用,虽然没有对每项应用进行详尽描述,但是希…

Ubuntu下通过CMake文件编译CUDA+OpenCV代码操作步骤
在 CUDA_Test 工程中,CUDA测试代码之前仅支持在Windows10 VS2013编译,今天在Ubuntu 14.04下写了一个CMakeLists.txt文件,支持在Linux下也可以通过CMake编译CUDA_Test工程,CMakeLists.txt文件内容如下:# CMake file f…

JAVA 多用户商城系统b2b2c-Spring Cloud常见问题与总结(一)
在使用Spring Cloud的过程中,难免会遇到一些问题。所以对Spring Cloud的常用问题做一些总结。需要JAVA Spring Cloud大型企业分布式微服务云构建的B2B2C电子商务平台源码 一零三八七七四六二六 一、Eureka常见问题 1.1 Eureka 注册服务慢 默认情况下,服务…
TinyFrame升级之八:实现简易插件化开发
本章主要讲解如何为框架新增插件化开发功能。 在.net 4.0中,我们可以在Application开始之前,通过PreApplicationStartMethod方法加载所需要的任何东西。那么今天我们主要做的工作就集中在这个时间段: 1.将插件DLL及文件拷贝入主网站目录并编译…
快手王华彦:端上视觉技术的极致效率及其短视频应用实践 | AI ProCon 2019
演讲嘉宾 | 王华彦(快手硅谷Y-tech实验室负责人) 编辑 | Just 出品 | AI科技大本营(ID:rgznai100) 快手用户日均上传1500万个视频,要把这些作品准确的分发给超2亿活跃用户,如果没有强大的AI技术系统去理解…
tmux简介及安装
tmux是一个开源工具,用于在一个终端窗口中运行多个终端会话。它可以减少过多的打开终端控制台。tmux的源码在 https://github.com/tmux/tmux ,它的License是BSD。tmux可以直接通过sudo apt-get install tmux命令安装(通过sudo apt-get remove tmux移除)…

Swift中依赖注入的解耦策略
原文地址:Dependency Injection Strategies in Swift 简书地址:Swift中依赖注入的解耦策略 今天我们将深入研究Swift中的依赖注入,这是软件开发中最重要的技术之一,也是许多编程语言中使用频繁的概念。 具体来说,我们将…

Eclipse mac 下的快捷键
2019独角兽企业重金招聘Python工程师标准>>> Eclipse,MyEclipse 的preference 在“windows”下边,mac下在左上角苹果图标边上 win下我们都习惯了ctrl c,在Mac 下使用标准键盘变成了win键c 系统的偏好设定 -> 键盘 -> 修饰…
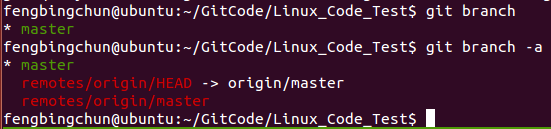
Ubuntu上使终端显示Git分支(oh-my-zsh)
oh-my-zsh是基于Zsh(Zsh是一个Linux用户很少使用的power-shell,这是由于大多数Linux产品安装,以及默认使用bash shell)的功能作了一个扩展,方便插件管理、主体自定义等。oh-my-zsh源码在 https://github.com/robbyrussell/oh-my-zsh &#x…

天哪!我的十一假期被AI操控了
(图片付费下载自视觉中国)导语:这个假期,除了脑海一直在唱歌,庆祝祖国成立的 70 周年,当然也闲不住,要乘机出去浪一浪。目前小长假进度条已经进行到 71.4% 了,有没有发现这个假期与以…
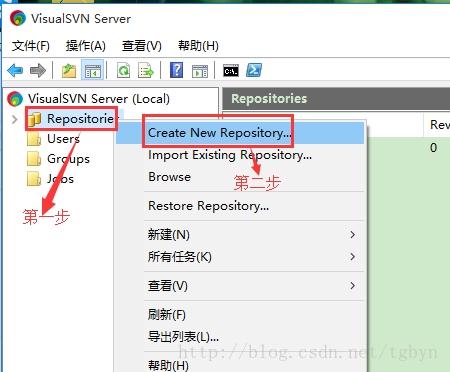
使用SVN+Axure RP 8.0创建团队项目
一、使用到的工具:VisualSVN Server --SVN服务器:https://www.visualsvn.com/server/ Axure RP 8.0 :http://www.downcc.com/soft/103078.html 二、VisualSVN Server 安装以及操作1、安装 : 默认安装即可 2、操作: &a…

no no no.不要使用kill -9.
2019独角兽企业重金招聘Python工程师标准>>> no no no.不要使用kill -9. 它没有给进程留下善后的机会: 1) 关闭socket链接 2) 清理临时文件 3) 将自己将要被销毁的消息通知给子进程 4) 重置自己的终止状态 等等。 通常,应该发送15,…

人工智能的“天罗地网”
(图片付费下载自视觉中国)整理 | 弯月编辑 | 郭芮来源 | CSDN(ID:CSDNnews)人工智能(AI)技术正在全球迅速崛起。不断涌现的最新发展令世人瞩目,从以假乱真的深度伪造视频,…
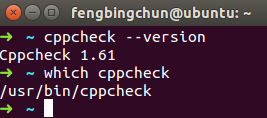
Ubuntu下安装Cppcheck源码操作步骤
Cppcheck是用在C、C中对code进行静态检查的工具。它的源码在 https://github.com/danmar/cppcheck 。它的License是GPL-3.0。Cppcheck可以检查不通过编译的文件,执行的检查包括:(1)、自动变量检查;(2)、数组的边界检查;(3)、clas…

用“脸”打卡,抬头就能签到!
科技正在飞速改变我们的生活,以前我们上班的时候,脖子上总会挂一个IC卡用来验证身份和签到打卡,后来指纹识别出现了,我们又逐渐习惯了指纹打卡,到如今,随着人脸识别技术的出现,我们开始用“脸”…

OC基础第四讲--字符串、数组、字典、集合的常用方法
OC基础第四讲--字符串、数组、字典、集合的常用方法 字符串、数组、字典、集合有可变和不可变之分。以字符串为例,不可变字符串本身值不能改变,必须要用相应类型来接收返回值;而可变字符串调用相应地方法后,本身会改变;…

分类、检测、分割任务均有SOTA表现,ACNet有多强?
(图片付费下载自视觉中国)作者 | 路一直都在来源 | 知乎专栏Abstract本文提出了一种新的自适应连接神经网络(ACNet),从两个方面对传统的卷积神经网络(CNNs)进行了改进。首先,ACNet通过自适应地确定特征节点之间的连接状态…

CUDA Samples: approximate prior vbox layer
以下CUDA sample是分别用C和CUDA实现的类似prior vbox layer的操作,并对其中使用到的CUDA函数进行了解说,各个文件内容如下:common.hpp:#ifndef FBC_CUDA_TEST_COMMON_HPP_ #define FBC_CUDA_TEST_COMMON_HPP_#include <typeinfo> #inc…

如何成为一名成功的 iOS 程序员?
前言: 编程是一个仅靠兴趣仍不足以抵达成功彼岸的领域。你必须充满激情,并且持之以恒地不断汲取更多有关编程的知识。只是对编程感兴趣还不足以功成名就——众所周知,我们工作起来像疯子。 编程是一个没有极限的职业,所以要成为一…

C#之委托与事件
委托与事件废话一堆:网上关于委托、事件的文章有很多,一千个哈姆雷特就有一千个莎士比亚,以下内容均是本人个人见解。1. 委托1.1 委托的使用这一小章来学习一下怎么简单的使用委托,了解一些基本的知识。这里先看一下其他所要用到的…

24式加速你的Python
作者 | 梁云1991来源 Python与算法之美一、分析代码运行时间第1式,测算代码运行时间平凡方法快捷方法(jupyter环境)第2式,测算代码多次运行平均时间平凡方法快捷方法(jupyter环境)第3式,按调用函…
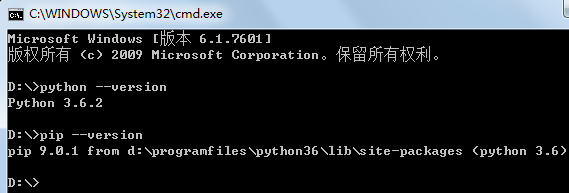
pip、NumPy、Matplotlib在Windows上的安装过程
Windows上Python 3.6.2 64位的安装步骤:1. 从 https://www.python.org/downloads/windows/ 下载Windows x86-64 executable installer(即python-3.6.2-amd64.exe);2. 直接以管理员身份运行安装,勾选添加到环境变量、pip等即可。可以同时在Wi…

分享:个人是怎么学习新知识的
为什么80%的码农都做不了架构师?>>> 挺多童鞋问我是怎么学习新知识的,干脆写篇文章总结一下,希望对大家有所帮助。对照书、技术博客、极客时间等学习的方式我就不说了。 一、早期 在15年及更早,由于知识储备少&#x…

easyui的datagrid
datagrid数据的绑定方式: 1)data 后跟数据行的json串 2)url 后跟{"total":,"rows":,"foot":},其中total代码返回总行数,rows为数据行json串 .NET MVC,controll控制类方法中获取datagrid…
线性回归介绍及分别使用最小二乘法和梯度下降法对线性回归C++实现
回归:在这类任务中,计算机程序需要对给定输入预测数值。为了解决这个任务,学习算法需要输出函数f:Rn→R。除了返回结果的形式不一样外,这类问题和分类问题是很像的。这类任务的一个示例是预测投保人的索赔金额(用于设置保险费)&am…
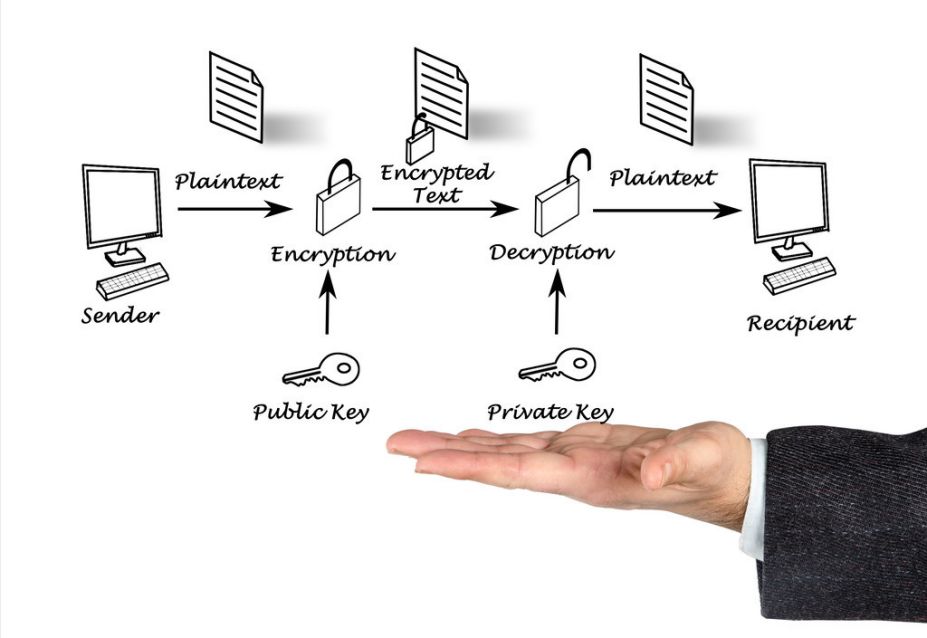
4种最常问的编码算法面试问题,你会吗?
导语:面试是测查和评价人员能力素质的一种考试活动。最常问的编码算法面试问题你知道多少呢?作者 | Rahul Sabnis译者 | 苏本如,编辑 | 刘静来源 | CSDN(ID:CSDNnews)在许多采访中,我经常被要求…

[小梅的体验课堂]Microsoft edge canary mac版本体验
简介 华硕微软越来越没有自己的JC了,不经在windows里面加了wsl而且还废弃了自己的老edge浏览器,重新基于chromium内核开发了新的edge浏览器了,不管怎么说mac上又多了一款新的浏览器,对于一个爱好新鲜的我来说那就简单安装体验下 下…

SQL Server用户自定义函数
用户自定义函数不能用于执行一系列改变数据库状态的操作,但它可以像系统 函数一样在查询或存储过程等的程序段中使用,也可以像存储过程一样通过EXECUTE 命令来执行。在 SQL Server 中根据函数返回值形式的不同将用户自 定义函数分为三种类型:…
