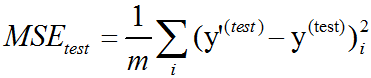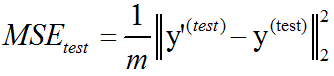线性回归介绍及分别使用最小二乘法和梯度下降法对线性回归C++实现

回归：在这类任务中，计算机程序需要对给定输入预测数值。为了解决这个任务，学习算法需要输出函数f:Rⁿ→R。除了返回结果的形式不一样外，这类问题和分类问题是很像的。这类任务的一个示例是预测投保人的索赔金额(用于设置保险费)，或者预测证券未来的价格。这类预测也用在算法交易中。

线性回归解决回归问题。换言之，我们的目标是建立一个系统，将向量x∈Rⁿ作为输入，预测标量y∈R作为输出。线性回归的输出是其输入的线性函数。另y’表示模型预测y应该取的值。我们定义输出为：y’=w^Tx, 其中w∈Rⁿ的参数(parameter)向量。

参数是控制系统行为的值。在这种情况下，w_i是系数，会和特征x_i相乘之后全部相加起来。我们可以将w看作是一组决定每个特征如何影响预测的权重(weight)。如果特征x_i对应的权重w_i是正的，那么特征的值增加，我们的预测值y’也会增加。如果特征x_i对应的权重w_i是负的，那么特征的值减少，我们的预测值y’也会减少。如果特征权重的大小很大，那么它对预测有很大的影响；如果特征权重的大小是零，那么它对预测没有影响。

因此，我们可以定义任务T：通过输出y’=w^Tx从x预测y。接下来我们需要定义性能度量P。

假设我们有m个输入样本组成的设计矩阵，我们不用它来训练模型，而是评估模型性能如何。我们也有每个样本对应的正确值y组成的回归目标向量。因为这个数据集只是用来评估性能，我们称之为测试集(test set)。我们将输入的设计矩阵记作X^(test)，回归目标向量记作y^(test)。

度量模型性能的一种方法是计算模型在测试集上的均方误差(mean squared error)。如果y’^(test)表示模型在测试集上的预测值，那么均方误差表示为：

直观上，当y’^(test)=y^(test)时，我们会发现误差降为0。我们也可以看到：

所以当预测值和目标值之间的欧几里得距离增加时，误差也会增加。

为了构建一个机器学习算法，我们需要设计一个算法，通过观察训练集(X^(train),y^(train))获得经验，减少MSE_test以改进权重w。一种直观方式是最小化训练集上的均方误差，即MSE_train。

最小化MSE_train，我们可以简单地求解其导数为0的情况：▽_wMSE_train=0

＝＞ w=(X^(train)TX^(train))^-1X^(train)Ty^(train)

上式给出解的系统方程被称为正规方程(normal equation)。计算上式构成了一个简单的机器学习算法。

线性回归(linear regression)通常用来指稍微复杂一些，附加额外参数(截距项b)的模型。在这个模型中，y’=w^Tx+b。因此从参数到预测的映射仍是一个线性函数，而从特征到预测的映射是一个仿射函数。如此扩展到仿射函数意味着模型预测的曲线仍然看起来像是一条直线，只是这条直线没必要经过原点。除了通过添加偏置参数b，我们还可以使用仅含权重的模型，但是x需要增加一项永远为1的元素。对应于额外1的权重起到了偏置参数的作用。

截距项b通常被称为仿射变换的偏置(bias)参数。这个术语的命名源自该变换的输出在没有任何输入时会偏移b。

在统计学中，线性回归(linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量的情况叫多元回归。

在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。

线性回归是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合，而且产生的估计的统计特性也更容易确定。

线性回归有很多实际用途。分为以下两大类：

(1)、如果目标是预测或者映射，线性回归可以用来对观测数据集和X的值拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的X值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。

(2)、给定一个变量y和一些变量X1,...,Xp，这些变量有可能与y相关，线性回归分析可以用来量化y与Xj之间相关性的强度，评估出与y不相关的Xj，并识别出哪些Xj的子集包含了关于y的冗余信息。

线性回归模型经常用最小二乘逼近来拟合，但也可用别的方法来拟合。最小二乘逼近也可以用来拟合那些非线性的模型。因此，尽管”最小二乘法”和”线性模型”是紧密相连的，但他们是不能划等号的。

理论模型：给一个随机样本(Y_i,X_i1,…,X_ip)，i=1,…,n，一个线性回归模型假设回归子Y_i和回归量X_i1,…,X_ip之间的关系是除了X的影响以外，还有其它的变数存在。我们加入一个误差项ε_i(也是一个随机变量)来捕获除了X_i1,…,X_ip之外任何对Yi的影响。所以一个多变量回归模型表示为以下的形式：

Y_i=β₀+β₁X_i1+β₂X_i2+…+β_pX_ip+ε_i,i=1,…,n.

其它的模型可能被认定成非线性模型。一个线性回归模型不需要是自变量的线性函数。线性在这里表示Y_i的条件均值在参数β里是线性的。例如：模型Y_i=β₁X_i+β₂X_i²+ε_i在β₁和β₂里是线性的，但在X_i²里是非线性的，它是X_i的非线性函数。

数据和估计：区分随机变量和这些变量的观测值是很重要的。通常来说，观测值或数据包括了n个值(y_i,x_i1,…,x_ip)，i=1,…,n. 我们有p+1个参数β₀,…, β_p需要决定，为了估计这些参数，使用矩阵标记：Y=Xβ+ε.其中Y是一个包括了观测值Y₁,…,Y_n的列向量，ε包括了未观测的随机成分ε₁,…, ε_n以及回归量的观测值矩阵X。X通常包括一个常数项。如果X列之间存在线性相关，那么参数向量β就不能以最小二乘法估计除非β被限制，比如要求它的一些元素之和为0。

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

以上内容主要摘自： 《深度学习中文版》 和  维基百科

以下是参考网上一些code分别通过最小二乘法和梯度下降法实现的线性回归C++测试代码：

linear_regression.hpp:

#ifndef NN_LINEAR_REGRESSION_HPP_
#define NN_LINEAR_REGRESSION_HPP_#include <memory>
#include <string>
#include <ostream>namespace ANN {typedef enum {LEAST_SQUARES = 0,GRADIENT_DESCENT
} regression_method;template<typename T>
class LinearRegression {template<typename U>friend std::ostream& operator << (std::ostream& out, const LinearRegression<U>& lr);public:LinearRegression() = default;void set_regression_method(regression_method method);int init(const T* x, const T* y, int length);int train(const std::string& model, T learning_rate = 0, int iterations = 0);int load_model(const std::string& model) const;T predict(T x) const; // y = wx+bprivate:int gradient_descent();int least_squares();int store_model() const;regression_method method;std::unique_ptr<T[]> x, y;std::string model = "";int iterations = 1000;int length = 0;T learning_rate = 0.001f;T weight = 0;T bias = 0;
};} // namespace ANN#endif // NN_LINEAR_REGRESSION_HPP_

linear_regression.cpp:

#include "linear_regression.hpp"
#include <fstream>
#include <random>
#include <algorithm>
#include <numeric>namespace ANN {template<typename T>
void LinearRegression<T>::set_regression_method(regression_method method)
{this->method = method;
}template<typename T>
int LinearRegression<T>::init(const T* x, const T* y, int length)
{if (length < 3) {fprintf(stderr, "number of points must be greater than 2: %d\n", length);return -1;}this->x.reset(new T[length]);this->y.reset(new T[length]);for (int i = 0; i < length; ++i) {this->x[i] = x[i];this->y[i] = y[i];}this->length = length;return 0;
}template<typename T>
int LinearRegression<T>::train(const std::string& model, T learning_rate, int iterations)
{this->learning_rate = learning_rate;this->iterations = iterations;this->model = model;if (this->method == LEAST_SQUARES) {least_squares();} else if (this->method == GRADIENT_DESCENT) {gradient_descent();} else {fprintf(stderr, "invalid linear regression method\n");return -1;}return store_model();
}template<typename T>
int LinearRegression<T>::store_model() const
{std::ofstream file;file.open(model.c_str(), std::ios::binary);if (!file.is_open()) {fprintf(stderr, "open file fail: %s\n", model.c_str());return -1;}int m = method;file.write((char*)&m, sizeof(m));file.write((char*)&weight, sizeof(weight));file.write((char*)&bias, sizeof(bias));file.close();return 0;
}template<typename T>
int LinearRegression<T>::load_model(const std::string& model) const
{std::ifstream file;file.open(model.c_str(), std::ios::binary);if (!file.is_open()) {fprintf(stderr, "open file fail: %s\n", model.c_str());return -1;}int m{ -1 };file.read((char*)&m, sizeof(m)* 1);file.read((char*)&weight, sizeof(weight)* 1);file.read((char*)&bias, sizeof(bias)* 1);file.close();return 0;
}template<typename T>
T LinearRegression<T>::predict(T x) const
{return weight * x + bias;
}template<typename T>
int LinearRegression<T>::gradient_descent()
{std::random_device rd; std::mt19937 generator(rd());std::uniform_real_distribution<T> distribution(0, 0.5);weight = distribution(generator);;bias = distribution(generator);;int count{ 0 };std::unique_ptr<T[]> error(new T[length]), error_x(new T[length]);for (int i = 0; i < iterations; ++i) {for (int j = 0; j < length; ++j) {error[j] = weight * x[j] + bias - y[j];error_x[j] = error[j] * x[j];}T error_ = std::accumulate(error.get(), error.get() + length, (T)0) / length;T error_x_ = std::accumulate(error_x.get(), error_x.get() + length, (T)0) / length;// error = p(i) - y(i)// bias(i+1) = bias(i) - learning_rate*errorbias = bias - learning_rate * error_;// weight(i+1) = weight(i) - learning_rate*error*xweight = weight - learning_rate * error_x_;++count;if (count % 100 == 0)fprintf(stdout, "iteration %d\n", count);}return 0;
}template<typename T>
int LinearRegression<T>::least_squares()
{T sum_x{ 0 }, sum_y{ 0 }, sum_x_squared{ 0 }, sum_xy{ 0 };for (int i = 0; i < length; ++i) {sum_x += x[i];sum_y += y[i];sum_x_squared += x[i] * x[i];sum_xy += x[i] * y[i];}if (fabs(length * sum_x_squared - sum_x * sum_x) > DBL_EPSILON) {weight = (length * sum_xy - sum_y * sum_x) / (length * sum_x_squared - sum_x * sum_x); // slopebias = (sum_x_squared * sum_y - sum_x * sum_xy) / (length * sum_x_squared - sum_x * sum_x); // intercept} else {weight = 0;bias = 0;}return 0;
}template<typename T>
std::ostream& operator << (std::ostream& out, const LinearRegression<T>& lr)
{out << "result: y = " << lr.weight << "x + " << lr.bias;return out;
}template std::ostream& operator << (std::ostream& out, const LinearRegression<float>& lr);
template std::ostream& operator << (std::ostream& out, const LinearRegression<double>& lr);
template class LinearRegression<float>;
template class LinearRegression<double>;} // namespace ANN

funset.cpp:

#include "funset.hpp"
#include <iostream>
#include "perceptron.hpp"
#include "BP.hpp""
#include "CNN.hpp"
#include "linear_regression.hpp"
#include "common.hpp"
#include <opencv2/opencv.hpp>int test_linear_regression_train()
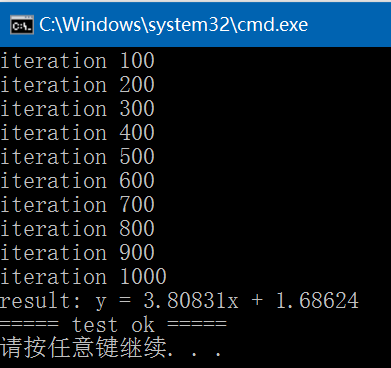
{std::vector<float> x{6.2f, 9.5f, 10.5f, 7.7f, 8.6f, 6.9f, 7.3f, 2.2f, 5.7f, 2.f,2.5f, 4.f, 5.4f, 2.2f, 7.2f, 12.2f, 5.6f, 9.f, 3.6f, 5.f,11.3f, 3.4f, 11.9f, 10.5f, 10.7f, 10.8f, 4.8f};std::vector<float> y{ 29.f, 44.f, 36.f, 37.f, 53.f, 18.f, 31.f, 14.f, 11.f, 11.f,22.f, 16.f, 27.f, 9.f, 29.f, 46.f, 23.f, 39.f, 15.f, 32.f,34.f, 17.f, 46.f, 42.f, 43.f, 34.f, 19.f };CHECK(x.size() == y.size());ANN::LinearRegression<float> lr;lr.set_regression_method(ANN::GRADIENT_DESCENT);lr.init(x.data(), y.data(), x.size());float learning_rate{ 0.001f };int iterations{ 1000 };std::string model{ "E:/GitCode/NN_Test/data/linear_regression.model" };int ret = lr.train(model, learning_rate, iterations);if (ret != 0) {fprintf(stderr, "train fail\n");return -1;}std::cout << lr << std::endl; // y = wx + breturn 0;
}
int test_linear_regression_predict()
{ANN::LinearRegression<float> lr;std::string model{ "E:/GitCode/NN_Test/data/linear_regression.model" };int ret = lr.load_model(model);if (ret != 0) {fprintf(stderr, "load model fail: %s\n", model.c_str());return -1;}float x = 13.8f;float result = lr.predict(x);fprintf(stdout, "input value: %f, result value: %f\n", x, result);return 0;
}

以下是调用梯度下降法得到的train结果：

以下是predict的结果：

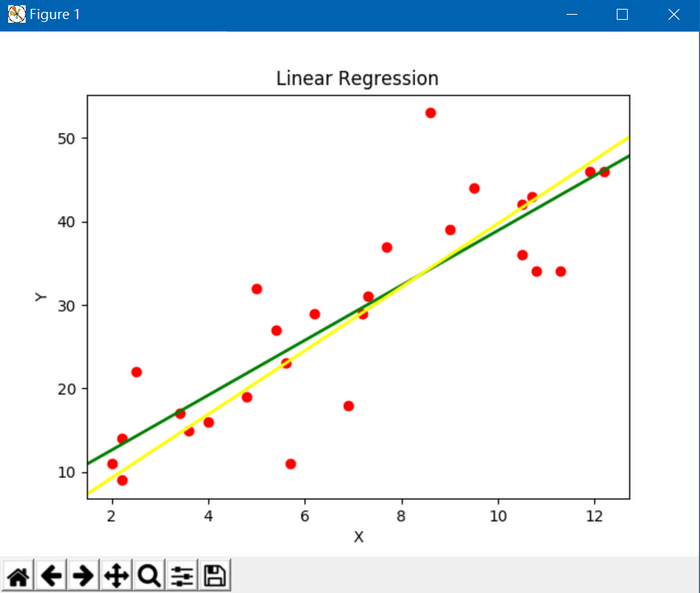
以下是通过Python实现的画曲线图：黄线是梯度下降法的结果，绿线是最小二乘法的结果

Python代码如下：

import numpy as np  
import matplotlib.pyplot as plt
from matplotlib.lines import Line2Dx = [6.2, 9.5, 10.5, 7.7, 8.6, 6.9, 7.3, 2.2, 5.7, 2.,2.5, 4., 5.4, 2.2, 7.2, 12.2, 5.6, 9., 3.6, 5.,11.3, 3.4, 11.9, 10.5, 10.7, 10.8, 4.8]
y = [29., 44., 36., 37., 53., 18., 31., 14., 11., 11.,22., 16., 27., 9., 29., 46., 23., 39., 15., 32.,34., 17., 46., 42., 43., 34., 19.]fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('Linear Regression')
plt.xlabel('X')
plt.ylabel('Y')
ax.scatter(x,y,c = 'r',marker = 'o')line1 = [(0.0, 6.0506), (40, 137.5202)] # least squares
line2 = [(0, 1.68624), (40, 154.01864)] # gradient descent(line1_xs, line1_ys) = zip(*line1)
(line2_xs, line2_ys) = zip(*line2)ax.add_line(Line2D(line1_xs, line1_ys, linewidth=2, color='green')) # least squares
ax.add_line(Line2D(line2_xs, line2_ys, linewidth=2, color='yellow')) # gradient descentplt.show()

GitHub： https://github.com/fengbingchun/NN_Test