一站式解决:隐马尔可夫模型(HMM)全过程推导及实现

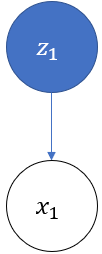
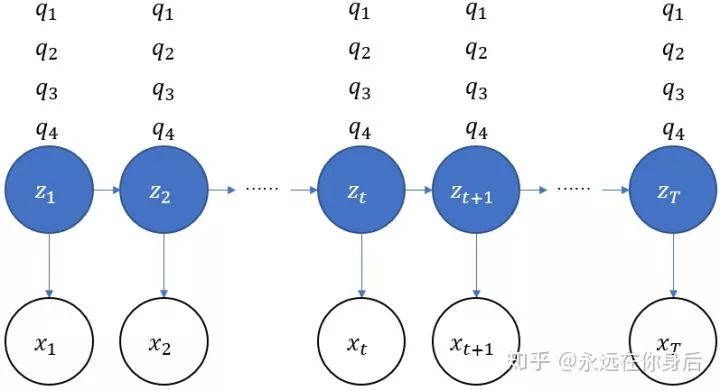
【导读】隐马尔可夫模型(Hidden Markov Model,HMM)是关于时许的概率模型,是一个生成模型,描述由一个隐藏的马尔科夫链随机生成不可观测的状态序列,每个状态生成一个观测,而由此产生一个观测序列。
定义抄完了,下面我们从一个简单的生成过程入手,顺便引出HMM的参数。
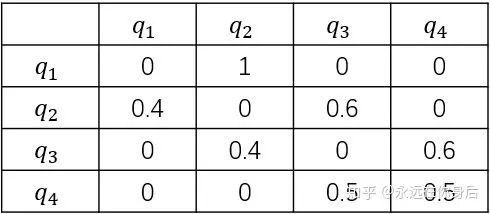
假设有4个盒子,每个盒子里面有不同数量的红、白两种颜色的球,具体如下表:
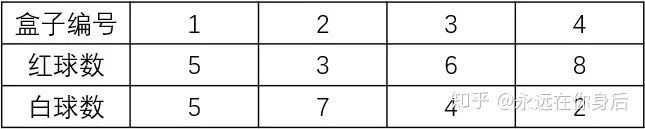
本栗子引用自《统计学习方法》
现在从这些盒子中抽取若干( )个球,每次抽取后记录颜色,再放回原盒子,采样的规则如下:
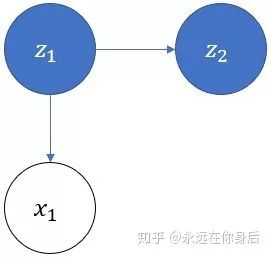
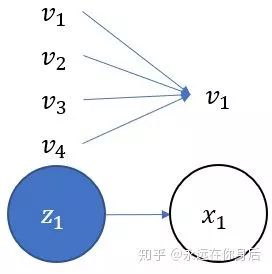
开始时,按照一个初始概率分布随机选择第一个盒子,这里将第一个盒子用 表示:

将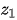 的值用变量
的值用变量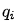 表示。因为有4个盒子可共选择,所以
表示。因为有4个盒子可共选择,所以 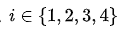 。然后随机从该盒子中抽取一个球,使用
。然后随机从该盒子中抽取一个球,使用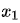 表示:
表示:
将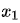 的值用变量
的值用变量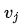 表示。因为只有两种球可供选择,所以
表示。因为只有两种球可供选择,所以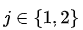 。一共有4个箱子,2种球,结合前面的箱子的详细数据,可以得到从每一个箱子取到各种颜色球的可能性,用一个表格表示:
。一共有4个箱子,2种球,结合前面的箱子的详细数据,可以得到从每一个箱子取到各种颜色球的可能性,用一个表格表示:
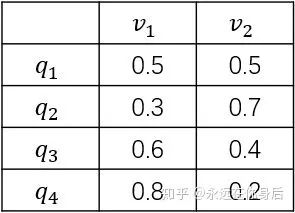
进一步,可以用一个矩阵(称为观测概率矩阵,也有资料叫做发射矩阵)来表示该表
其中 表示在当前时刻给定 的条件下,给定
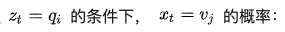
表示当前的时刻,例如现在是第1时刻;然后是前面标注的初始概率分布,这个概率分布可以用一个向量(称作初始状态概率向量)来表示:
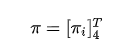
其中的
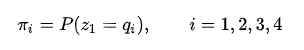
例如该分布是均匀分布的话,对应的向量就是
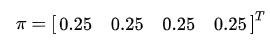
记录抽取的球的颜色后将其放回,然后在按照如下规则选择下一个盒子(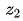 ):
):
- 如果当前是盒子1,则选择盒子2
- 如果当前是盒子2或3,则分布以概率0.4和0.6选择前一个或后一个盒子
- 如果当前是盒子4,则各以0.5的概率停留在盒子4或者选择盒子3
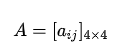

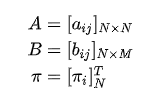
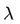 表示所有的参数。下面,根据这个栗子,写一个数据生成代码
表示所有的参数。下面,根据这个栗子,写一个数据生成代码import numpy as np class HMM(object): def __init__(self, N, M, pi=None, A=None, B=None): self.N = N self.M = M self.pi = pi self.A = A self.B = B def get_data_with_distribute(self, dist): # 根据给定的概率分布随机返回数据(索引) r = np.random.rand() for i, p in enumerate(dist): if r < p: return i r -= p def generate(self, T: int): ''' 根据给定的参数生成观测序列 T: 指定要生成数据的数量 ''' z = self.get_data_with_distribute(self.pi) # 根据初始概率分布生成第一个状态 x = self.get_data_with_distribute(self.B[z]) # 生成第一个观测数据 result = [x] for _ in range(T-1): # 依次生成余下的状态和观测数据 z = self.get_data_with_distribute(self.A[z]) x = self.get_data_with_distribute(self.B[z]) result.append(x) return result if __name__ == "__main__": pi = np.array([.25, .25, .25, .25]) A = np.array([ [0, 1, 0, 0], [.4, 0, .6, 0], [0, .4, 0, .6], [0, 0, .5, .5]]) B = np.array([ [.5, .5], [.3, .7], [.6, .4], [.8, .2]]) hmm = HMM(4, 2, pi, A, B) print(hmm.generate(10)) # 生成10个数据 # 生成结果如下
[0, 0, 1, 1, 1, 1, 0, 1, 0, 0] # 0代表红球,1代表白球
- 齐次马尔可夫假设:即任意时刻的状态只依赖于前一时刻的状态,与其他时刻的状态无关(当然,初始时刻的状态由参数π决定):
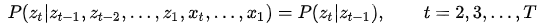
- 观测独立假设:即任意时刻的观测只依赖于该时刻的状态,与其他无关:概率计算算法
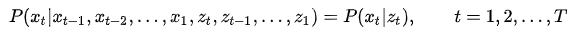
概率计算算法
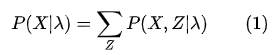
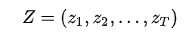
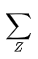 展开得到:
展开得到: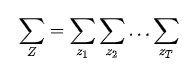
即使不考虑内部的计算,这起码也是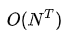 阶的计算量,所以需要更有效的算法,下面介绍两种:前向算法和后向算法。
阶的计算量,所以需要更有效的算法,下面介绍两种:前向算法和后向算法。
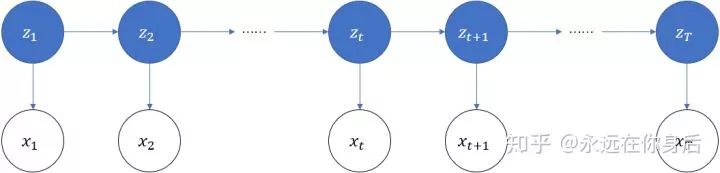
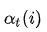 ,它t时刻的状态以及1,2,...t时刻的观测在给定参数下的联合概率:
,它t时刻的状态以及1,2,...t时刻的观测在给定参数下的联合概率: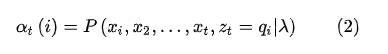
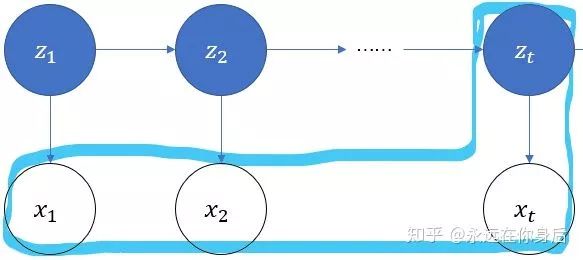
也就是下图中标记的那一部分
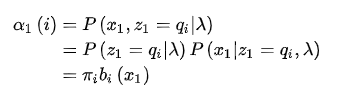
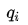 生成给定观测数据的概率,例如设t时刻观测数据
生成给定观测数据的概率,例如设t时刻观测数据 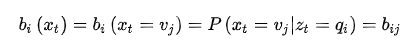
接着,根据(2)式,还可以得到:
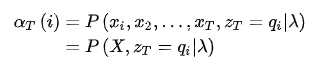
由此公式,遍历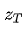 的取值求和,可以得到
的取值求和,可以得到 的边际概率
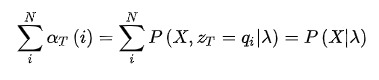

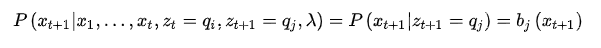
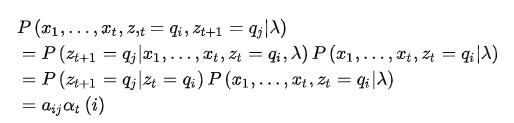
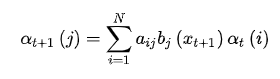
class HMM(object): def evaluate(self, X): ''' 根据给定的参数计算条件概率 X: 观测数据 ''' alpha = self.pi * self.B[:,X[0]] for x in X[1:]: # alpha_next = np.empty(self.N) # for j in range(self.N): # alpha_next[j] = np.sum(self.A[:,j] * alpha * self.B[j,x]) # alpha = alpha_next alpha = np.sum(self.A * alpha.reshape(-1,1) * self.B[:,x].reshape(1,-1), axis=0) return alpha.sum() print(hmm.evaluate([0,0,1,1,0])) # 0.026862016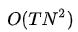 ,比之前至少
,比之前至少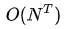 的起步价已经好太多了.
的起步价已经好太多了.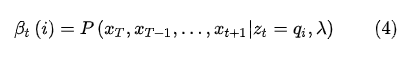

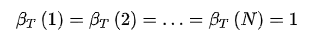
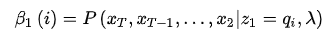

 的定义。实际上,对于任意时刻t,存在以下等式
的定义。实际上,对于任意时刻t,存在以下等式
 。而红色部分,根据假设2,
。而红色部分,根据假设2, 都是无关(即互相独立),可以省去,所以这部分最终变为:
都是无关(即互相独立),可以省去,所以这部分最终变为: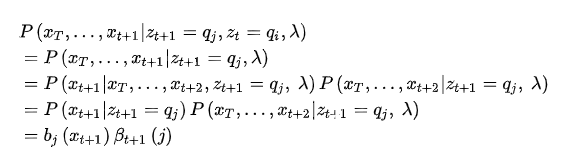

def evaluate_backward(self, X): beta = np.ones(self.N) for x in X[:0:-1]: beta_next = np.empty(self.N) for i in range(self.N): beta_next[i] = np.sum(self.A[i,:] * self.B[:,x] * beta) beta = beta_next return np.sum(beta * self.pi * self.B[:,X[0]])学习算法

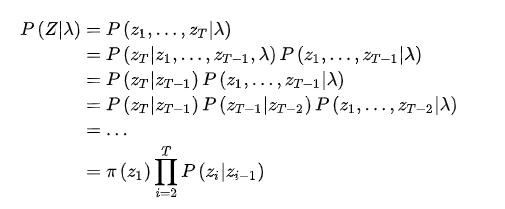

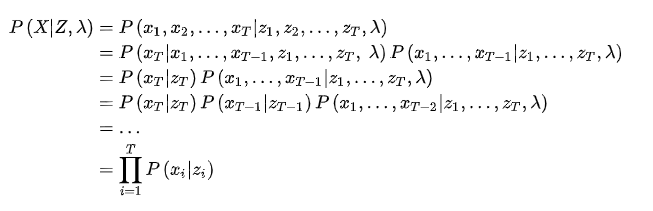
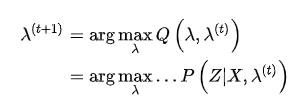

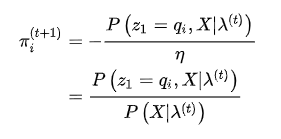
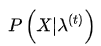 就是当前参数下观测数据的概率,就是第一个问题所求解的。另外,利用第一个问题中定义的前向概率和后向概率,有:
就是当前参数下观测数据的概率,就是第一个问题所求解的。另外,利用第一个问题中定义的前向概率和后向概率,有: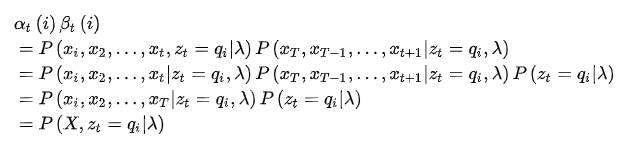
最终得到:
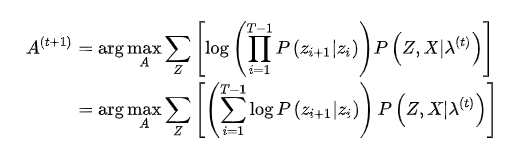
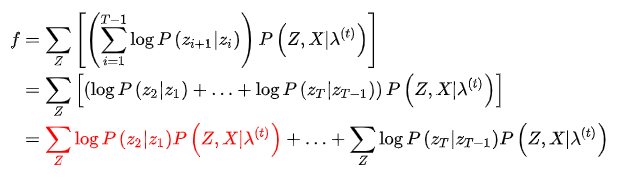
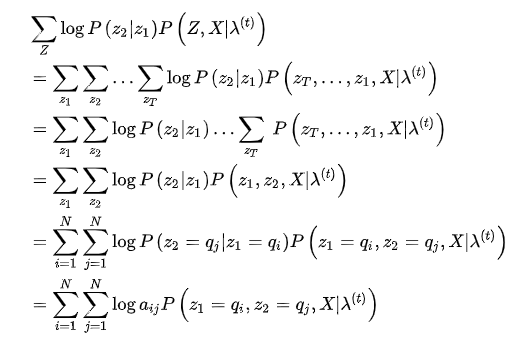
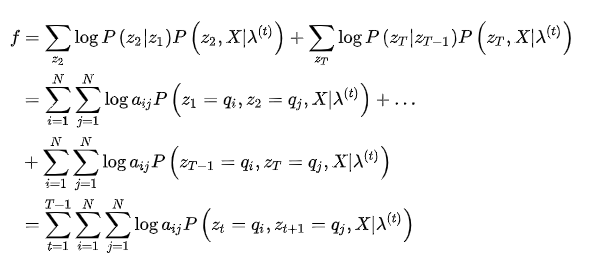

同样,使用拉格朗日乘数法,构造目标函数
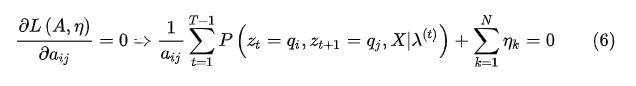
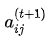
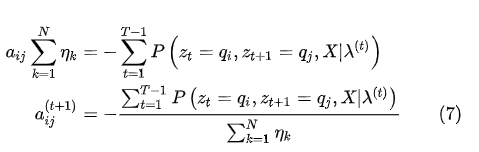
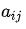 的约束,代入(6)式,得到:
的约束,代入(6)式,得到: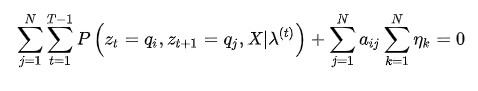
然后化简:
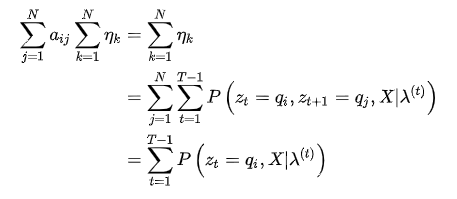
代入(7)式,得到
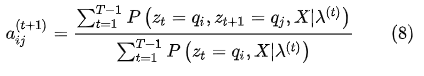
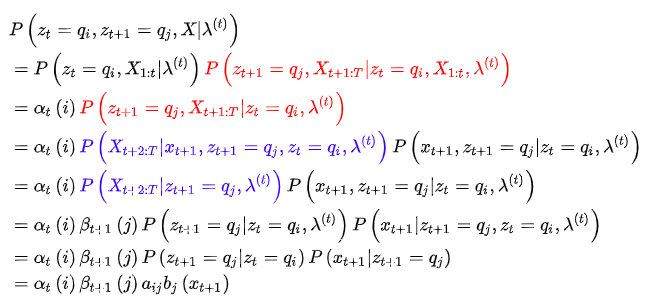
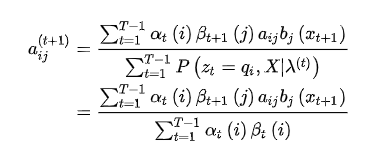

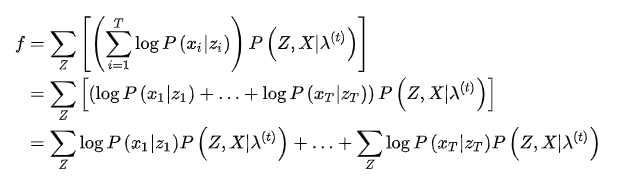
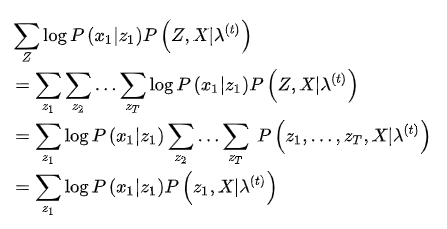
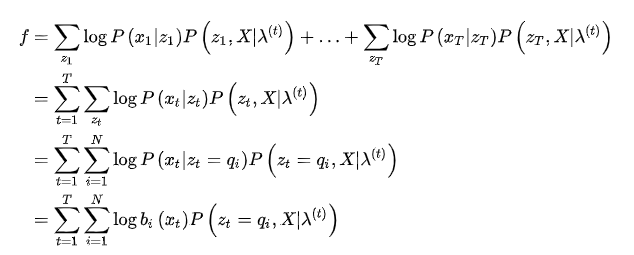

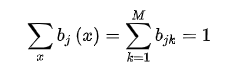
M是矩阵B的列数,前面已经定义过的,构造拉格朗日函数:
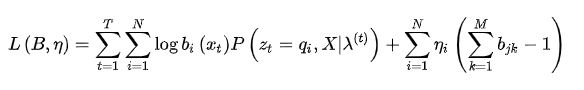
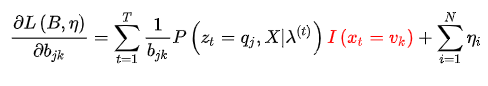

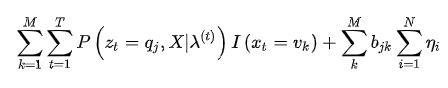

class HMM(object): def fit(self, X): ''' 根据给定观测序列反推参数 ''' # 初始化参数 pi, A, B self.pi = np.random.sample(self.N) self.A = np.ones((self.N,self.N)) / self.N self.B = np.ones((self.N,self.M)) / self.M self.pi = self.pi / self.pi.sum() T = len(X) for _ in range(50): # 按公式计算下一时刻的参数 alpha, beta = self.get_something(X) gamma = alpha * beta for i in range(self.N): for j in range(self.N): self.A[i,j] = np.sum(alpha[:-1,i]*beta[1:,j]*self.A[i,j]*self.B[j,X[1:]]) / gamma[:-1,i].sum() for j in range(self.N): for k in range(self.M): self.B[j,k] = np.sum(gamma[:,j]*(X == k)) / gamma[:,j].sum() self.pi = gamma[0] / gamma[-1].sum() def get_something(self, X): ''' 根据给定数据与参数,计算所有时刻的前向概率和后向概率 ''' T = len(X) alpha = np.zeros((T,self.N)) alpha[0,:] = self.pi * self.B[:,X[0]] for i in range(T-1): x = X[i+1] alpha[i+1,:] = np.sum(self.A * alpha[i].reshape(-1,1) * self.B[:,x].reshape(1,-1), axis=0) beta = np.ones((T,self.N)) for j in range(T-1,0,-1): for i in range(self.N): beta[j-1,i] = np.sum(self.A[i,:] * self.B[:,X[j]] * beta[j]) return alpha, beta if __name__ == "__main__": import matplotlib.pyplot as plt def triangle_data(T): # 生成三角波形状的序列 data = [] for x in range(T): x = x % 6 data.append(x if x <= 3 else 6-x) return data data = np.array(triangle_data(30)) hmm = HMM(10, 4) hmm.fit(data) # 先根据给定数据反推参数 gen_obs = hmm.generate(30) # 再根据学习的参数生成数据 x = np.arange(30) plt.scatter(x, gen_obs, marker='*', color='r') plt.plot(x, data, color='g') plt.show()预测算法



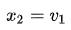 ,末端的计算自然还是一样
,末端的计算自然还是一样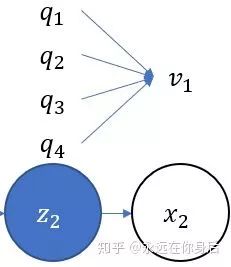
 如何计算最大概率
如何计算最大概率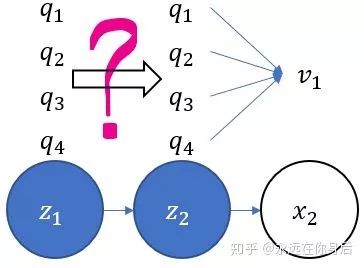

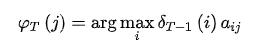
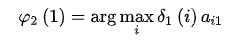

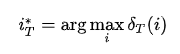

class HMM(object): def decode(self, X): T = len(X) x = X[0] delta = self.pi * self.B[:,x] varphi = np.zeros((T, self.N), dtype=int) path = [0] * T for i in range(1, T): delta = delta.reshape(-1,1) # 转成一列方便广播 tmp = delta * self.A varphi[i,:] = np.argmax(tmp, axis=0) delta = np.max(tmp, axis=0) * self.B[:,X[i]] path[-1] = np.argmax(delta) # 回溯最优路径 for i in range(T-1,0,-1): path[i-1] = varphi[i,path[i]] return path◆
精彩推荐
◆

推荐阅读
确认!语音识别大牛Daniel Povey将入职小米,曾遭霍普金斯大学解雇,怒拒Facebook
大规模1.4亿中文知识图谱数据,我把它开源了
自动驾驶关键环节:行人的行为意图建模和预测(上)
不足 20 行 Python 代码,高效实现 k-means 均值聚类算法
巨头垂涎却不能染指,loT 数据库风口已至
【建议收藏】数据中心服务器基础知识大全
从4个维度深度剖析闪电网络现状,在CKB上实现闪电网络的理由 | 博文精选
身边程序员同事竟说自己敲代码速度快!Ctrl+C、Ctrl+V ?
100 美元一行代码,开源软件到底咋赚钱?

你点的每个“在看”,我都认真当成了AI
相关文章:

CUDA Samples: Image Process: BGR to BGR565
图像像素格式BGR565是每一个像素占2个字节,其中Blue占5位,Green占6位,Red占5位。在OpenCV中,BGR到BGR565的每一个像素的计算公式是:unsigned short dst (unsigned short)((B >> 3) | ((G & ~3) << 3)…

NoSQL数据库探讨 - 为什么要用非关系数据库?
源地址:http://robbin.javaeye.com/blog/524977 随着互联网web2.0网站的兴起,非关系型的数据库现在成了一个极其热门的新领域,非关系数据库产品的发展非常迅速。而传统的关系数据库在应付web2.0网站,特别是超大规模和高并发的SNS类…

手机内存RAM、ROM简介
手机内存包含两个:一个是运行内存(RAM),一个是机身内存(ROM)。两者的功能有所不同,运行内存是对手机操作系统和其它程序运行过程中,产生的临时数据进行存储的媒介。如果手机运行的程序比较多,占用运行内存空间较大&…

一个月入门Python爬虫,轻松爬取大规模数据
如果你仔细观察,就不难发现,懂爬虫、学习爬虫的人越来越多,一方面,互联网可以获取的数据越来越多,另一方面,像 Python这样一个月入门Python爬虫,轻松爬的编程语言提供越来越多的优秀工具&#x…

软件包管理 之 软件在线升级更新yum 图形工具介绍
作者:北南南北来自:LinuxSir.Org提要:yum 是Fedora/Redhat 软件包管理工具,包括文本命令行模式和图形模式;图形模式的yum也是基于文本模式的;目前yum图形前端程序主要有 yumex和kyum ; 正文一、…

[PHPUnit]自动生成PHPUnit测试骨架脚本-提供您的开发效率【2015升级版】
2019独角兽企业重金招聘Python工程师标准>>> 场景 在编写PHPUnit单元测试代码时,其实很多都是对各个类的各个外部调用的函数进行测试验证,检测代码覆盖率,验证预期效果。为避免增加开发量,可以使用PHPUnit提供的phpuni…

ORL Faces Database介绍
ORL人脸数据集共包含40个不同人的400张图像,是在1992年4月至1994年4月期间由英国剑桥的Olivetti研究实验室创建。此数据集下包含40个目录,每个目录下有10张图像,每个目录表示一个不同的人。所有的图像是以PGM格式存储,灰度图&…

张俊林:BERT和Transformer到底学到了什么 | AI ProCon 2019
演讲嘉宾 | 张俊林(新浪微博机器学习团队AI Lab负责人)编辑 | Jane出品 | AI科技大本营(ID:rgznai100)【导读】BERT提出的这一年,也是NLP领域迅速发展的一年。学界不断提出新的预训练模型,刷新各…
Eclipse创建web工程时,报错Dynamic Web Module 3.0 requires Java 1.6 or newer.
报错: 解决方案: 1.打开eclipse工具栏window->preferences 2.打开java->compiler 3.选择compiler compliance level在1.6以上版本(此处选择1.8) 4.点击apply and close保存修改,即可 转载于:https://www.cnblogs…

Maven学习总结(八)——使用Maven构建多模块项目
2019独角兽企业重金招聘Python工程师标准>>> Maven学习总结(八)——使用Maven构建多模块项目 在平时的Javaweb项目开发中为了便于后期的维护,我们一般会进行分层开发,最常见的就是分为domain(域模型层)、dao࿰…

哈工大、清华、CSDN、嵌入式视觉联盟合办的 AIoT 盛会,你怎么舍得错过?!
2019 嵌入式智能国际大会即将来袭!随着物联网和人工智能技术的飞速发展与相互渗透,万物智联的新赛道已经开始显现。据中商产业研究院《2016—2021年中国物联网产业市场研究报告》显示,预计到2020年,中国物联网的整体规模将达2.2万…

OpenCV3.3中主成分分析(Principal Components Analysis, PCA)接口简介及使用
OpenCV3.3中给出了主成分分析(Principal Components Analysis, PCA)的实现,即cv::PCA类,类的声明在include/opencv2/core.hpp文件中,实现在modules/core/src/pca.cpp文件中,其中:(1)、cv::PCA::PCA:构造函数࿱…

Spring MVC配置
为什么80%的码农都做不了架构师?>>> 一、传统方式配置Spring MVC (1)导入jar包 需要导入如下的jar包 junit-3.8.1.jar spring-core-3.0.5.RELEASE.jar commons-logging-1.1.1.jar spring-context-3.0.5.REL…
主成分分析(PCA)Python代码实现
主成分分析(Principal Components Analysis, PCA)简介可以参考: http://blog.csdn.net/fengbingchun/article/details/78977202 这里是参照 http://sebastianraschka.com/Articles/2014_pca_step_by_step.html 文章中的code整理的Python代码,实现过程为…

AI发展这一年:不断衍生的技术丑闻与抵制声潮
作者 | AI Now学院译者 | Raku编辑 | Jane出品 | AI科技大本营(ID: rgznai100)【导读】10月2日,纽约大学AI Now学院在纽约大学斯克博剧院(Skirball Theatre)组织召开了第四届年度AI Now研讨会。研讨会邀请了业内组织者…

Distributed Configuration Management Platform(分布式配置管理平台)
2019独角兽企业重金招聘Python工程师标准>>> 专注于各种 分布式系统配置管理 的通用组件/通用平台, 提供统一的配置管理服务。 主要目标: 部署极其简单:同一个上线包,无须改动配置,即可在 多个环境中(RD/QA/PRODUCTION…

如何利用zendstudio新建 或导入php项目
为什么80%的码农都做不了架构师?>>> 一、利用ZendStudio创建 PHP Project 1. 打开ZendStudio, 选择:File à New à PHP Project, 如下图所示: 于是弹出如下界面: 在”Project name”后输入工程名(比如我这里…

一文读懂GoogLeNet神经网络 | CSDN博文精选
作者 | .NY&XX来源 | CSDN博客本文介绍的是著名的网络结构GoogLeNet,目的是试图领会其中结构设计思想。GoogLeNet特点优化网络质量的生物学原理GoogLeNet网络结构的动机GoogLeNet架构细节Inception模块和普通卷积结构的差异辅助分类器GoogLeNet网络架构GoogLeNe…

C++中的函数签名
C中的函数签名(function signature):包含了一个函数的信息,包括函数名、参数类型、参数个数、顺序以及它所在的类和命名空间。普通函数签名并不包含函数返回值部分,如果两个函数仅仅只有函数返回值不同,那么系统是无法区分这两个函…

MyEclipse断点调试
2019独角兽企业重金招聘Python工程师标准>>> 1、在编辑的程序的左边,你会看到一条浅浅的灰色编带,在这里设置断点。 2、设置断点的方法有很多 方法:1)、双击 ; 2)、右键,选择“Toggl…

C primer plus 练习题 第三章
5. 1 #include <stdio.h>2 3 int main()4 {5 float you_sec;6 printf("请输入你的年龄:");7 scanf("%f", &you_sec);8 printf("年龄合计:%e 秒!\n", you_sec * 3.156e7);9 getchar(); 10 return 0; 11 }

Echache整合Spring缓存实例讲解
2019独角兽企业重金招聘Python工程师标准>>> 摘要:本文主要介绍了EhCache,并通过整合Spring给出了一个使用实例。 一、EhCache 介绍 EhCache 是一个纯Java的进程内缓存框架,具有快速、精干等特点,是Hibernate中默认的C…
灰度图像直方图均衡化公式及实现
图像的直方图:直方图是图像中像素强度分布的图形表达方式。它统计了每一个强度值所具有的像素个数。直方图均衡化:是通过拉伸像素强度分布范围来增强图像对比度的一种方法。是图像处理领域中利用图像直方图对对比度进行调整的方法。均衡化指的是把一个分…
超越最新无监督域自适应方法,研究人员提轻量CNN新架构OSNet
作者 | Kaiyang Zhou, Xiatian Zhu, Yongxin Yang, Andrea Cavallaro, and Tao Xiang 译者 | TroyChang 编辑 | Jane 出品 | AI科技大本营(ID:rgznai100) CNN新架构OSNet 【导读】今天推荐论文《Learning Generalisable Omni-Scale Repre…

在一台机器上搭建多个redis实例
2019独角兽企业重金招聘Python工程师标准>>> 默认Redis程序安装在/usr/local/redis目录下; 配置文件:/usr/local/redis/redis.conf,该配置文件中配置的端口为默认端口:6379; Redis的启动命令路径࿱…

使用kaptcha生成验证码
2019独角兽企业重金招聘Python工程师标准>>> kaptcha是一个简单好用的验证码生成工具,通过配置,可以自己定义验证码大小、颜色、显示的字符等等。下面就来讲一下如何使用kaptcha生成验证码以及在服务器端取出验证码进行校验。 一、搭建测试环…

主成分分析(PCA) C++ 实现
主成分分析(Principal Components Analysis, PCA)简介可以参考: http://blog.csdn.net/fengbingchun/article/details/78977202以下是PCA的C实现,参考OpenCV 3.3中的cv::PCA类。使用ORL Faces Database作为测试图像。关于ORL Faces Database的介绍可以参…

为何Google、微软、华为将亿级源代码放一个仓库?从全球最大代码管理库说起...
作者 | 夕颜编辑 | Just出品 | AI 科技大本营(ID:rgznai100)【导读】2017 年,在当时微软的一篇官方博客中,时任微软云开发服务副总裁的 Brian Harry 表示微软内部代码开始向 Git 迁移,宣布推出针对大规模 repo 的“Git…

jquery mobie导致超链接不可用
在a标签中添加rel"external"即可转载于:https://blog.51cto.com/here2142/1435434

编译器GCC与Clang的异同
GCC:GNU(Gnus Not Unix)编译器套装(GNU Compiler Collection,GCC),指一套编程语言编译器,以GPL及LGPL许可证所发行的自由软件,也是GNU项目的关键部分,也是GNU工具链的主要组成部分之一。GCC(特别是其中的C语…
