从AdventureWorks学习数据库建模——保留历史数据
在业务需求中,经常需要我们在系统中能够记录历史信息,能够查看到历史变动情况,这时我们可以通过增加开始结束时间字段来记录数据的历史版本。对数据的历史记录主要分为:关系、属性历史,实体历史和变更历史。
关系、属性历史记录
所谓关系历史记录就是指两个实体之间的关系存在历史版本。比如部门表和员工表,对于某一个时刻来说,一个部门有多个员工,一个员工只属于一个部门,所以是个一对多的关系。而我们希望把这个关系记录下历史变动,那么就会形成多对多关系。多对多关系就形成中间表,然后我们在中间表上加入“开始时间”字段和“结束时间”字段即可记录这个关系的历史。
对某个实体的属性记录历史记录会形成一对多的关系表,比如产品价格属性,我们希望把所有历史定价都记录下来,那么就会形成产品和价格一对多的关系。
在AdventureWorks数据库中,我们可以看到大量的这种记录关系历史的设计。比如:
员工、部门、轮班的历史记录:
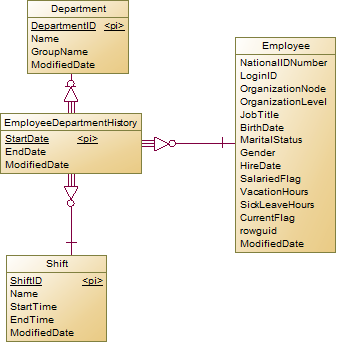
这就是前面提到的一对多关系因为记录历史变为多对多关系的例子。
产品对成本和售价的历史记录:
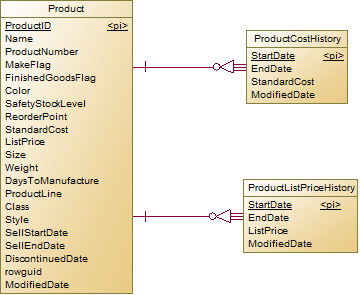
这就是典型的属性历史记录,对于产品的众多属性,我们之关系成本和售价这两个属性的历史,所有可以建立一对多关系的价格历史表。
销售和区域以及销售配额的历史记录:
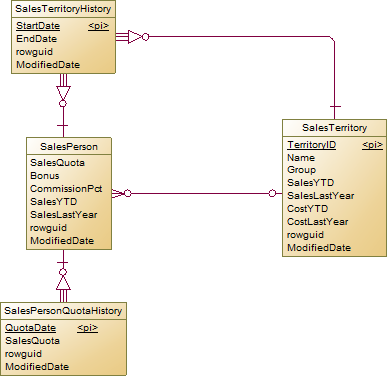
区域和销售本来也是普通的一对多关系,一个销售属于某个片区,一个区域对应多个销售。现在由于历史记录,所以形成多对多的关系表SalesTerritoryHistory。而对于销售配额,因为是记录到季度的,一季度只有一个销售配额,所以不需要开始时间和结束时间,只需要一个季度第一天即可(结束时间是可以根据这个季度的第一天而计算出来的,所以不需要再存储)。
区域与销售人员的关系在增加了中间表形成多对多后,仍然保留了原来的一对多关系,从数据上来看不是这样的,因为两个表的数据是不一致的,所以我推断这是另外一个一对多关系,而不是原来的区域和销售的分配对应关系表。
小结:
当需要对关系或属性记录历史时,会把关系提升一个复杂度,也就是说原来是一对一的,现在会变成一对多,原来是一对多的,现在会变成多对多。在历史记录表中增加“开始时间”和“结束时间”两个字段来表示该行数据的时间有效性。AdventureWorks数据库中使用了NULL值设为“结束时间”来表明这条数据是当前有效的,但是笔者并不推荐这么做,最好是把两个字段都设置为NOT NULL,在比较时可以得到统一的查询语句:
另外SalesTerritoryHistory这个表只记录“开始时间”而不记录“结束时间”这也是一个不好的设计,虽然结束时间是可以计算出来的,但是每次查询的时候还需要去计算结束时间,真不是一个好方法。最好是把两个字段都保留,用户只需要输入开始时间,由前端程序去初始化结束时间,然后一并保存。
实体历史记录
主实体历史记录
实体的历史记录是指对一个实体数据的任何更改,都把整条数据都产生一条新记录,而不是只针对某个属性或者关系。对实体进行历史记录,我们也可以采用添加开始时间结束时间的方式,但是更多的时候我们对整个实体记录历史并不是为了随时查询历史上某个时间点这个实体的值,而是为了记录一个“版本Version”信息,方便在审计某个实体的变更时对比。如果我们是出于审计的需要而记录的历史版本,那么这些历史数据平时是不会参与到业务查询中的,所以并不需要记录开始时间,结束时间,取而代之的,我们可以增加“版本”字段,当然还有审计用到的“最后更新时间”和“最后更新人”,
这样就实体的变化情况,如果我们仅仅是增加Version字段,在查询当前版本时会很麻烦,因为我们必须拿到最高的那个版本号,然后才能把这个最新版本的记录作为当前记录,为了优化这个性能问题,我们一般还需要再添加布尔型的“是否当前版本IsCurrent”字段来标识当前版本。增加了这个字段后,那么在更改实体数据时就会更麻烦一些。首先需要将老数据版本号获得,+1生成新的版本号,然后将老数据的“是否当前版本”字段置为0,更新老数据的“最后更新时间”和“最后更新人”,然后插入新版本号的数据,而且新版本是当前版本。我在AdventureWorks数据库中并没有看到关于实体的历史记录的设计,不过我们可以看SharePoint的数据库设计,就是采用我这里提到的版本设计的方法。有兴趣的可以查看一下SharePoint的ContentDB的AllUserData表,tp_Version就是记录版本的,tp_IsCurrent和tp_IsCurrentVersion就是标记当前版本的。
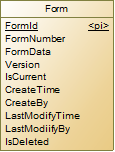
附属实体的历史记录
在进行实体历史记录时,还面临的一个问题是,附属的子实体是否也需要一并进行历史记录。比如我们要对采购订单这么一个实体进行历史记录,每次对采购订单的修改都会生成一个新版本的采购订单。如果一个采购订单下面有100条采购明细,那么我们在编辑了采购订单主表后,创建了新版本的采购主表数据,是否对这100条明细也创建对应的新版本数据呢?如果创建,那么采购明细表的数据量就会飞涨,而且实际上我们这里并没有编辑这100条明细,新版本的明细数据是一模一样的,如果不创建,那么怎么保持这种外键约束呢?毕竟明细表上面的外键对应的可是老版本的采购订单的ID啊!
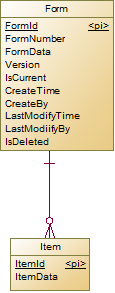
其实两种方案都可以,第一种方案开发简单,如果明细并不是那么多,或者本身单据的数据量并不大,那么重复一点明细表并不会带来太大的影响。第二种方案开发会很复杂,需要新老数据逐条对比,找到差异,如果主表有更改,那么为主表创建新版本,如果100条明细中有2条更改,那么就为这2条创建新版本。
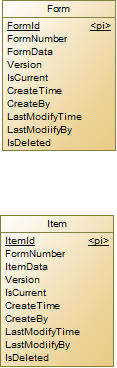
下面详细说一下采用第二种的解决方案的模型设计。首先,我们需要断开主表和附属表的外键,将Form和Item作为两个独立的实体,各自添加“版本”,“是否当前版本”等属性。为Form添加业务主键“FormNumber”,用于唯一标识一个表单(由于版本记录的原因,所以FormNumber不是Form的主键),然后在Item表中添加“FormNumber”,用于标识这些Item是属于哪个表单。
from Form
where IsCurrent=1 and IsDeleted=0 and FormNumber=@formNumber;
select *
from Item
where IsCurrent=1 and IsDeleted=0 and FormNumber=@formNumber;
变更历史记录
无论前面讲到的对关系,属性还是整个实体的历史记录,都会在业务表中形成新的数据,数据的增加一方面会导致查询的效率变低,另一方面也使得每次查询时都需要带上额外的查询条件,非常不方便。于是我们想到了另一种保存历史记录的方式,那就是我们像记录日志一样,把变更了的部分记录到日志表中。
记录变更日志的好处是不影响现有数据库模型的设计,也就是说所有实体和关系都不需要改,我们只需要增加一个变更日志表即可。但是变更日志一般是前端程序通过对比前后记录,找到变更的属性,然后写入的,并不是数据库做的事。坏处也显而易见,那就是还原历史数据不方便,不能像前面的模型那样可以快速的查询数据的历史状态。
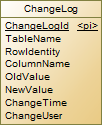
所以变更日志表这种处理方式只用于审计的需求,而不能用于业务上要对历史数据的查询需求。在AdventureWorks数据库中有一个TransactionHistory表,用于记录各个订单事务的,虽然不是记录订单变更的,但是也有和变更历史记录类似的结构。
历史数据查询优化
前面提到由于保留历史数据的原因,所以会将数据库中对应表的数据量增加很多倍,数据量的增加必然导致查询变慢,所以我们在记录历史数据后很有必要对表进行查询优化。优化可以采用以下解决方案:
归档表
如果我们的历史数据在平时的业务中并不需要,只有在特殊场景才会用到历史数据表,那么我们可以将历史数据表建立一模一样结构的归档表,然后定时将业务系统中的历史数据转移到归档表中。当然,前端软件系统也要做对应的修改,对于老的历史数据需要查询归档表,而新的数据是查询当前表。在AdventureWorks只对TransactionHistory就建立了对应的归档表。

分区
建立分区比归档表的好处是在物理上,老数据和新数据可以存储在不同的地方,新老数据可以各自建立各自的索引树,而在逻辑上对程序来说仍然是访问一个表,前端程序不需要做什么修改。比如对于开始结束日期的历史数据记录方式,我们可以把结束日期为9999-12-31的数据(当前有效数据)分到一个区,剩下的分到另一个区。对于版本记录的方式,我们可以将“是当前版本”分到一个区,把其他的数据分到另一个区。
分区后在更新数据时会导致老数据的区块转移,因为老数据本来是在Current区块的,现在由于更改了实体,老数据需要转移到Old区块,然后将新数据插入到Current区块,除了分区的移动还有对应的索引的变动,所以更新数据时会相对慢一些。
索引
如果对于Oracle数据库,那么我们可以对IsCurrentVersion字段建立位图索引,如果是SQL Server这种不支持位图索引的数据库,那么我们也可以在建立B树索引时把IsCurrentVersion放在第一列,因为这个列是必然放入过滤条件的。
相关文章:

因特网的域名服务器系统的好处,dns域名服务器的作用是什么
大家好,我是智能客服时间君,上述问题将由我为大家进行解答。dns是域名系统 (Domain Name System) 的缩写,该系统用于命名组织到域层次结构中的计算机和网络服务。DNS 命名用于Internet等TCP/IP网络中,通过用户友好的名称查找计算机…

Openssl私建CA
构建私有CA: 在确定配置为CA的服务上生成一个自签证书,并为CA提供所需要的目录及文件即可;步骤: (1) 生成私钥;[rootcentos7 ~]# (umask 077; openssl genrsa -out /etc/pki/CA/private/cakey.pem 4096)Generating RSA priva…

不同版本浏览器前端标准兼容性对照表以及CORS解决跨域和CSRF安全问题解决方案
CORS也已经成为主流的跨域解决方案,不过CORF也会引发CSRF,本文先分享第三方的一个前端工具箱全面展示那些浏览器版本支持CORS,由于各家浏览器厂商因为各自原因在不同的版本里支持的标准不同,这个工具小而美,可以清晰的…

arm服务器获取文件路径中文,ssh 访问远程服务器文件路径
ssh 访问远程服务器文件路径 内容精选换一换在IntelliJ上选择“项目”,找到“.idea”文件夹,单击右键选择“新建>文件”, 输入文件名“settings.json”生成settings.json文件。如图1所示。复制以下代码至新创建的settings.json文件中&…

[Win7]如何还原[.bat]文件关联
2019独角兽企业重金招聘Python工程师标准>>> 此文已迁移到微信公众号:灰灰的Rom笔记,公众号ID:SXF-Rom。 灰灰的Rom笔记 转载于:https://my.oschina.net/shawnxia/blog/672371

Android Monkey使用
Monkey 是什么? Android SDK自带的压力测试工具,也是一个命令行工具。它向系统发送伪随机的用户事件流(如按键输入,触摸屏输入,手势输入等),实现对正在开发的应用程序进行压力测试。 ࿰…

Flink在美团的应用与实践听课笔记
本文系《Flink在美团的应用与实践》的听课笔记 原始视频视频资源已经在优酷公开:2018.8.11 Flink China Meetup北京站-Flink在美团的应用与实践 作者:刘迪珊美团 1.现状和背景 实时平台架构 最底层是数据缓存层,可以看到美团测的所有日志类…

[LeetCode]题解(python):150-Evaluate Reverse Polish Notation
题目来源: https://leetcode.com/problems/evaluate-reverse-polish-notation/ 题意分析: 给定一个数组,用这个数组来表示加减乘除,例如 ["2", "1", "", "3", "*"] -> ((2 …

微软苹果服务器宕机,苹果服务器宕机,iPhone用户别做这两项操作,微软特斯拉也中招...
原标题:苹果服务器宕机,iPhone用户别做这两项操作,微软特斯拉也中招虽然苹果一直都以安全来标榜自己,而事实上也确实如此。IOS封闭的环境,相对与安卓这个开放的环境确实要更加安全一些。苹果可以很好的抵御外来的风险&…
索尼发布无人机相机专利,支持眼部对焦
无人机将采用可折叠式设计,无需使用手机就能操控。 目前消费级无人机的行业霸主自然是大疆无疑,前段时间推出的Mavic 2再次让我们领略了大疆无人机的实力。不过近日,索尼在日本公布了其首个无人机相机专利技术,似乎在向大疆发起挑…
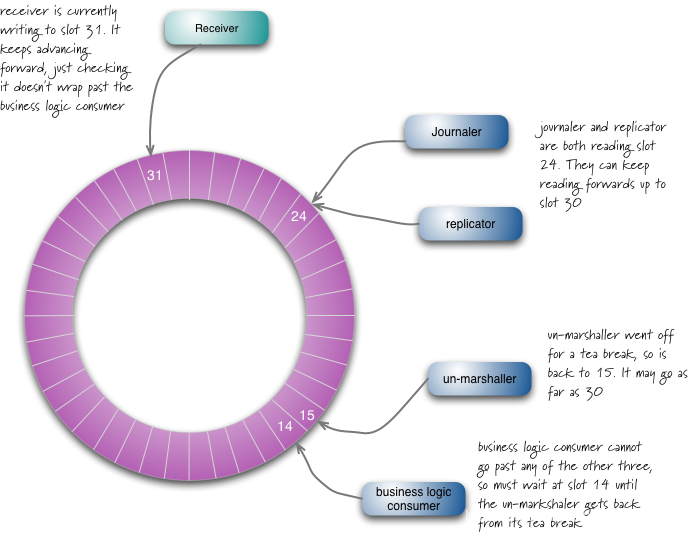
你需要知道的高性能并发框架Disruptor原理
Disruptor的小史 现在要是不知道Disruptor真的已经很outer了,Disruptor是英国外汇交易公司LMAX开发的一款开源的高性能队列,LMAX Disruptor是一个高性能的线程间消息传递库,它源于LMAX对并发性,性能和非阻塞算法的研究࿰…

c++11 多线程 1c++ concurrency in action
一、并行、多线程 1、计算机中的并行有两种方式:任务切换、利用多处理器多核。 纯粹的任务切换: 纯粹的多处理器多核: 任务切换与多处理器多核结合: 实际应用中是“任务切换与多处理器多核结合”方式,首先现在硬件偏移…

芯片刀片服务器,使用“刀片服务器”其实不难
刀片服务器已经轰轰烈烈地吵了将近两年的时间,市场上的刀片服务器产品也越来越多,所使用的芯片种类也逐渐发展为intel、amd、power等几种,支持的平台也包括了unix和ia架构。2005年底,hp还推出了基于安腾2平台的bl60p产品ÿ…

Prometheus 对比 Zabbix
公司要上监控,Prometheus 是最热门的监控解决方案,作为喜新厌旧的程序员,我当然是选择跟风了,但上级更倾向于 Zabbix,那没办法,只能好好对比一番,给出几个靠谱的理由了。 但稍稍深入一点&#x…

好理解的Java内存虚假共享(False Sharing)性能损耗以及解决方案
虚假共享(False Sharing)也有人翻译为伪共享 参考 https://en.wikipedia.org/wiki/False_sharing 在计算机科学中,虚假共享是一种性能降低的使用模式,它可能出现在具有由高速缓存机制管理的最小资源块大小的分布式一致高速缓存的系统中。当系统参与者将…

delphi xe 文件服务器,DelphiXE7中创建WebService(服务端+客户端)
相关资料:http://www.2ccc.com/news/Html/?1507.htmlhttp://www.dfwlt.com/forum.php?modviewthread&tid922DelphiXE7新建WebService具体操作:1.打开“DelphiXE7”->“File”->“New”->“Other”2.“New Items”->“Delph…

Android app 别用中文名
/************************************************************************** Android app 别用中文名* 说明:* 本来想分析一下这份源代码,结果发现因为项目名中有中文不能自动生成R* 文件,于是不想分析了。** …
一线互联网常见的14个Java面试题,你颤抖了吗程序员
跳槽不算频繁,但参加过不少面试(电话面试、face to face面试),面过大/小公司、互联网/传统软件公司,面糊过(眼高手低,缺乏实战经验,挂掉),也面过人࿰…

复化梯形公式,Newton-Cotes公式,变量代换后的复化梯形公式,Gauss-Legendre公式,Gauss-Jacobi公式插值积分的精确度比较
1.问题 分别计算积分 Ic∫01cosxxdx1.809048475800...I_c\int_0^1\frac{\cos{x}}{\sqrt{x}}dx1.809048475800... Ic∫01xcosxdx1.809048475800... Is∫01sinxxdx0.620536603446I_s\int_0^1\frac{\sin{x}}{\sqrt{x}}dx0.620536603446 Is∫01xsinxdx0.62053…

Elasticsearch 知识点目录
2019独角兽企业重金招聘Python工程师标准>>> 经过一段时间的编写,完成了第一个版本的Elasticsearch书籍的编写,目录结构如下: 1 Elasticsearch入门 7 1.1 Elasticsearch是什么 7 1.1.1 Elasticsearch是什么 7 1.1.2 Elasticsearch…

不要千言万语,一组漫画让你秒懂最终一致性
直接上图 如果你以前看过最终一致性的定义那么你一定会为这幅精彩漫画拍手叫好。 你要是不知道什么是最终一致性你可以看看下面的权威定义,当然了网上关于什么是最终一致性的帖子铺天盖地,也许你已经很明白了,即使这样你是不是依然为此图欢呼…

Feign实现服务调用
上一篇博客我们使用ribbonrestTemplate实现负载均衡调用服务,接下来我们使用feign实现服务的调用,首先feign和ribbon的区别是什么呢? ribbon根据特定算法,从服务列表中选取一个要访问的服务; RoundRobinRule:轮询RandomRule:随机Availability…

度量,跟踪和日志记录
今天,我有幸参加了2017年的分布式追踪峰会,其中有很多来自AWS / X-Ray,OpenZipkin,OpenTracing,Instana,Datadog,Librato等公司的人员,我很遗憾我忘记了这一点。有一次讨论转向了项目…

python 第六章 函数 pta(1)
1.Multiple-Choice 1.print(type(lambda:3))的输出结果是____。 A.<class ‘function’> B.<class ‘int’> C.<class ‘NoneType’> D.<class ‘float’> 答案:A 2.在Python中,对于函数定义代码的理解,正确的理解…
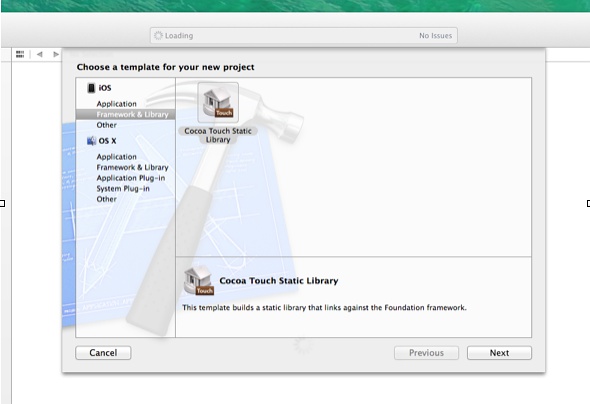
生成.a文件步骤
1.新建一个Project 选择 iOS->Framework & Library ->Cocoa Touch Static Library点击Next-> 输入Product Name 2.删除自动生成的文件 替换成我们需要的文件 如:原本自定生成的文件为继承自NSObject的,而你需要的为继承自UIView的ÿ…
机器学习之优雅落地线性回归法
在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析维基百科。简单线性回归当只有一个自变量的时候,成为简单线性回归。简单线性回归模型的思…
SpringBoot整合Grpc实现跨语言RPC通讯
什么是gRPC gRPC是谷歌开源的基于go语言的一个现代的开源高性能RPC框架,可以在任何环境中运行。它可以有效地连接数据中心内和跨数据中心的服务,并提供可插拔的支持,以实现负载平衡,跟踪,健康检查和身份验证。它还适用…

python 第六章 函数
1.函数的定义 def 名称(形参): 函数体 2.函数的调用 名称(实参) 单独文件:模块 调用方式——模块.名称 3.函数的参数类型 1.位置参数: def add(a,b):add(2,3) #顺序,个数,数据类型都要相同!!…
C++简单使用Jsoncpp来读取写入json文件
一、源码编译 C操作json字符串最好的库应该就是jsoncpp了,开源并且跨平台。它可以从这里下载。 下载后将其解压到任意目录,它默认提供VS2003和VS2010的工程文件,使用VS2010可以直接打开makefiles\msvc2010目录下的sln文件。 工程文件提供Json…

BZOJ 3420: Poi2013 Triumphal arch
二分答案 第二个人不会走回头路 那么F[i]表示在i的子树内(不包括i)所需要的额外步数 F[1]0表示mid可行 k可能为0 #include<cstdio> #include<algorithm> using namespace std; int cnt,n,mid,F[300005],last[300005]; struct node{int to,next; }e[600005]; void a…
