机器学习之优雅落地线性回归法
在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析维基百科。
简单线性回归
当只有一个自变量的时候,成为简单线性回归。
简单线性回归模型的思路
为了得到一个简单线性回归模型,假设存在以房屋面积为特征,以价格为样本输出,包含四个样本的样本集,如图:
寻找一条直线,最大程度上拟合样本特征与样本输出之间的关系。
假设最佳拟合的直线方程为:,则对于样本特征
的每一个取值
的预测值为:
。而我们希望的就是真值
和预测值
之间的差距尽量小。
可以用 表示两者之间的差距,对于所有的样本,使用求和公式求和处理:
∑ i =1 m | y ( i) −y ^ ( i) |
但是这个公式有一个问题,不容易求导,为了解决这个问题,可先对 进行平方,如此最后的公式就变成了:
∑ i =1 m (y ( i) −y ^ ( i) ) 2
最后,替换掉 ,即为:
∑ i =1 m (y ( i) −a x ( i) −b ) 2
因此,找到的一个简单线性回归模型就是找到合适的 a 和 b,使得该函数的值尽可能的小,该函数也称为损失函数(loss function)。
最小二乘法
找到合适的 a 和 b,使得 的值尽可能的小,这样的方法称为最小二乘法。
如何求 a 和 b 呢?令该函数为 ,分别使对 a 和 b 求导的结果为0。
对 b 求导:,得:
b =y ¯ ¯ ¯ −a x ¯ ¯ ¯
对 a 求导:,得:
a =∑ m i =1 (x ( i) −x ¯ ¯ ¯ )(y ( i) −y ¯ ¯ ¯ ) ∑ m i =1 (x ( i) −x ¯ ¯ ¯ ) 2
注:这里略去了公式的推导过程。还有很多内容因为篇幅有限不详细写了,如果想全面了解的可以点击这个链接跳转到我已经录制好的视频
简单线性回归的实现
有了数学的帮助,实现简单线性回归就比较方便了。
首先声明一个样本集:
import numpy as npx = np.array([1., 2., 3., 4., 5.]) y = np.array([1., 3., 2., 3., 5.])
公式中用到了 x 和 y 的均值:
x_mean = np.mean(x) y_mean = np.mean(y)
求 a 和 b 的值有两种方法。第一种是使用 for 循环:
# 分子 num = 0.0# 分母 d = 0.0for x_i, y_i in zip(x, y):num += (x_i - x_mean) * (y_i - y_mean)d += (x_i - x_mean) ** 2a = num / d b = y_mean - a * x_mean
第二种是使用矩阵乘:
num = (x - x_mean).dot(y - y_mean) d = (x - x_mean).dot(x - x_mean)a = num / d b = y_mean - a * x_mean
注:使用矩阵乘效率更高。
求出了 a 和 b,简单线性模型就有了:。对当前示例作图表示:
衡量线性回归法的指标
误差
一个训练后的模型通常都会使用测试数据集测试该模型的准确性。对于简单线性归回模型当然可以使用 来衡量,但是它的取值和测试样本个数 m 存在联系,改进方法很简单,只需除以 m 即可,即均方误差(Mean Squared Error):
M SE : 1 m ∑ i =1 m (y ( i) t est −y ^ ( i) t est ) 2
np.sum((y_predict - y_true) ** 2) / len(y_true)
值得一提的是 MSE 的量纲是样本单位的平方,有时在某些情况下这种平方并不是很好,为了消除量纲的不同,会对 MSE 进行开方操作,就得到了均方根误差(Root Mean Squared Error):
R MS E: 1 m ∑ i =1 m (y ( i) t est −y ^ _t est ( i) ) 2 − −− −− −− −− −− −− −− −− −− √ =M SE t es t − −− −− −− √
import mathmath.sqrt(np.sum((y_predict - y_true) ** 2) / len(y_true))
还有一种衡量方法是平均绝对误差(Mean Absolute Error),对测试数据集中预测值与真值的差的绝对值取和,再取一个平均值:
M AE : 1 m ∑ i =1 m | y ( i) t es t −y ^ ( i) t es t |
np.sum(np.absolute(y_predict - y_true)) / len(y_true)
注:Scikit Learn 的 metrics 模块中的 mean_squared_error() 方法表示 MSE,mean_absolute_error() 方法表示 MAE,没有表示 RMSE 的方法。
R Squared
更近一步,MSE、RMSE 和 MAE 的局限性在于对模型的衡量只能做到数值越小表示模型越好,而通常对模型的衡量使用1表示最好,0表示最差,因此引入了新的指标:R Squared,计算公式为:
R 2 =1 −S S r es i d u al S S t ot a l
,表示使用模型产生的错误;
,表示使用
预测产生的错误。
更深入的讲,对于每一个预测样本的 x 的预测值都为样本的均值 ,这样的模型称为基准模型;当我们的模型等于基准模型时,
的值为0,当我们的模型不犯任何错误时
得到最大值1。
还可以进行转换,转换结果为:
R 2 =1 −M SE ( y ^ ,y ) V ary
实现也很简单:
1 - np.sum((y_predict - y_true) ** 2) / len(y_true) / np.var(y_true)
注:Scikit Learn 的 metrics 模块中的 r2_score() 方法表示 R Squared。
多元线性回归
多元线性回归模型的思路
当有不只一个自变量时,即为多元线性回归,如图:
对于有 n 个自变量来说,我们想获得的线性模型为:
y =θ 0 +θ 1 x 1 +θ 2 x 2 +.. .+θ n x n
根据简单线性回归的思路,我们的目标即为:
找到 ,
,
,...,
,使得
尽可能的小,其中
。
:训练数据中第 i 个样本的预测值;
:训练数据中第 i 个样本的第 j 个自变量。
如果用矩阵表示即为:
y ^ ( i) =X ( i) ⋅θ
其中:;
。
更进一步,将 也使用矩阵表示,即为:
y ^ =X b ⋅θ
其中:,
因此,我们目标就成了:使 尽可能小。而对于这个公式的解,称为多元线性回归的正规方程解(Nomal Equation):
还有很多内容因为篇幅有限不详细写了,如果想全面了解的可以点击这个链接跳转到我已经录制好的视频
θ =(X T b Xb ) − 1 (X T b y )
实现多元线性回归
将多元线性回归实现在 LinearRegression 类中,且使用 Scikit Learn 的风格。
_init_() 方法首先初始化线性回归模型,_theta 表示 ,
interception_ 表示截距,chef_ 表示回归模型中自变量的系数:
class LinearRegression:def __init__(self):self.coef_ = Noneself.interceiption_ = Noneself._theta = None
fit_normal() 方法根据训练数据集训练模型,X_b 表示添加了 的样本特征数据,并且使用多元线性回归的正规方程解求出
:
def fit_normal(self, X_train, y_train):X_b = np.hstack([np.ones((len(X_train), 1)), X_train])self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)self.interception_ = self._theta[0]self.coef_ = self._theta[1:]return self
predict() 方法为预测方法,同样使用了矩阵乘:
def predict(self, X_predict):X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])return X_b.dot(self._theta)
score() 根据给定的测试数据集使用 R Squared 指标计算模型的准确度:
def score(self, X_test, y_test):y_predict = self.predict(X_test)return r2_score(y_test, y_predict)
Scikit Learn 中的线性回归实现放在 linear_model 模块中,使用方法如下:
from sklearn.linear_model import LinearRegression
线性回归的特点
线性回归算法是典型的参数学习的算法,只能解决回归问题,其对数据具有强解释性。
缺点是多元线性回归的正规方程解 的时间复杂度高,为
,可优化为
。
转载于:https://blog.51cto.com/14014179/2313081
相关文章:
SpringBoot整合Grpc实现跨语言RPC通讯
什么是gRPC gRPC是谷歌开源的基于go语言的一个现代的开源高性能RPC框架,可以在任何环境中运行。它可以有效地连接数据中心内和跨数据中心的服务,并提供可插拔的支持,以实现负载平衡,跟踪,健康检查和身份验证。它还适用…

python 第六章 函数
1.函数的定义 def 名称(形参): 函数体 2.函数的调用 名称(实参) 单独文件:模块 调用方式——模块.名称 3.函数的参数类型 1.位置参数: def add(a,b):add(2,3) #顺序,个数,数据类型都要相同!!…
C++简单使用Jsoncpp来读取写入json文件
一、源码编译 C操作json字符串最好的库应该就是jsoncpp了,开源并且跨平台。它可以从这里下载。 下载后将其解压到任意目录,它默认提供VS2003和VS2010的工程文件,使用VS2010可以直接打开makefiles\msvc2010目录下的sln文件。 工程文件提供Json…

BZOJ 3420: Poi2013 Triumphal arch
二分答案 第二个人不会走回头路 那么F[i]表示在i的子树内(不包括i)所需要的额外步数 F[1]0表示mid可行 k可能为0 #include<cstdio> #include<algorithm> using namespace std; int cnt,n,mid,F[300005],last[300005]; struct node{int to,next; }e[600005]; void a…
Java泛型使用需要小心
这是源自实际开发的一个坑,只是被我简化了。 Set<Integer> gs null;Set gss new HashSet();gs gss;gss.add("19");System.out.println(gs);for (int i : gs) {if (i19) {System.out.println("1");}} 代码经过一些转换你如果不注意以…

证明实对称正定矩阵A的Gauss-Seidel法必定收敛(完整过程)
Solution: \quad将nnn阶实对称矩阵AAA设为D−L−LTD-L-L^TD−L−LT,其中DDD是AAA的所有主对角元素构成对角矩阵,−L-L−L是AAA的所有主对角线以下的元素构成的严格下三角矩阵。 \quad此时Gauss−SeidelGauss-SeidelGauss−Seidel法的迭代矩阵为(D−L)−1LT(…

5月中旬的一些总结
考完英语口语了,最大的帮助就是找到了练习的方法和思路。 周三晚上有谷歌的全球IO大会。 ******** 写吴斌老师的课程作业,这才发现winedt过期了。用了rept之后本来是解决问题了,可是一联网就又不行了。总要关上再打开。用防火墙阻断却找不到选…

项目总结10:通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题...
通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题 关键字 springboot热部署 ClassCastException异常 反射 redis 前言 最近项目出现一个很有意思的问题,用户信息(token)储存在redis中;在获取token,反序列…

Rouche Theorem(Stein复分析)
Rouche Theorem: \quadIffandgareholomorphicfunctionsinaregionΩcontainingacircleCanditsinterior,and∣f(z)∣≥∣g(z)∣forz∈C,fandfghavethesamenumbersofzerosinsidethecircleC.If\quad f\quad and\quad g\quad are\quad holomorphic\quad functions\quad i…

Java线上程序频繁JVM FGC问题排障与启示
线上Java程序的JVM频繁FGC,现象如图所示: 一直持续FGC 5次左右,每次耗时1秒多不等。 FGC的原因实际上是内存不够用,但是运维反映堆内存是2G,从运维提供的参数看也是。 内存实际上一直只用到1G以内。 这时候可以自己写…

python常用数据结构的常用操作
作为基础练习吧。列表LIST,元组TUPLE,集合SET,字符串STRING等等,显示,增删,合并。。。 #List shoplist [apple,mango,carrot,banana] print I have ,len(shoplist), items to purchase. print These items are: for …

h5 和native 交互那些事儿
前端菜菜一枚,写下关于h5 和native 交互那些事情。偏前端,各种理论知识,不在赘述。之前有各位大牛已经写过。我只写代码,有问题,下面留言/* 关于h5 和native 之间的交互 JSBridge 解决问题,偏向前端* 使用U…

手把手教你写电商爬虫-第二课 实战尚妆网分页商品采集爬虫
系列教程 手把手教你写电商爬虫-第一课 找个软柿子捏捏 如果没有看过第一课的朋友,请先移步第一课,第一课讲了一些基础性的东西,通过软柿子"切糕王子"这个电商网站好好的练了一次手,相信大家都应该对写爬虫的流程有了一…

Python程序设计 第六章 函数(续
复习 1. 10进制 ⇒\Rightarrow⇒ 2进制 除2取余,从低位到高位存储到字符串中,从高位到低位def d2b(n):if n>1:d2b(n//2)print(n%2,end)d2b(4)出口: 条件,值确定 (一)return (二)函数体执行结…

K8S的横向自动扩容的功能Horizontal Pod Autoscaling
K8S 作为一个集群式的管理软件,自动化、智能化是免不了的功能。Google 在 K8S v1.1 版本中就加入了这个 Pod 横向自动扩容的功能(Horizontal Pod Autoscaling,简称 HPA)。 HPA 与之前的 Deployment、Service 一样,也属…
第八周例行报告
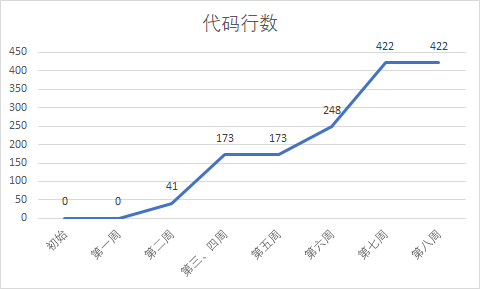
此作业要求参见:https://edu.cnblogs.com/campus/nenu/2018fall/homework/2326 1、本周PSP 类型 任务 开始时间 结束时间 中断时间 Delta时间 会议 事后诸葛亮会议 11.3 14:12 11.3 15:08 0min 56min 博客 编写博客《事后诸葛…

HTTP头部信息解释分析(详细整理)
这篇文章为大家介绍了HTTP头部信息,中英文对比分析,还是比较全面的,若大家在使用过程中遇到不了解的,可以适当参考下 HTTP 头部解释 1. Accept:告诉WEB服务器自己接受什么介质类型,*/* 表示任何类型&#…

深圳杯---深圳市生活垃圾处理社会总成本分析
2017年3月18日,国务院向全国发布了《生活垃圾分类制度实施方案》,这标志着中国垃圾分类制度建设开始了一个全新阶段,垃圾分类已成为推进社会经济绿色发展、提升城市管理和服务水平、优化人居环境的重要举措。为了保证这一目标能够顺利实现&am…
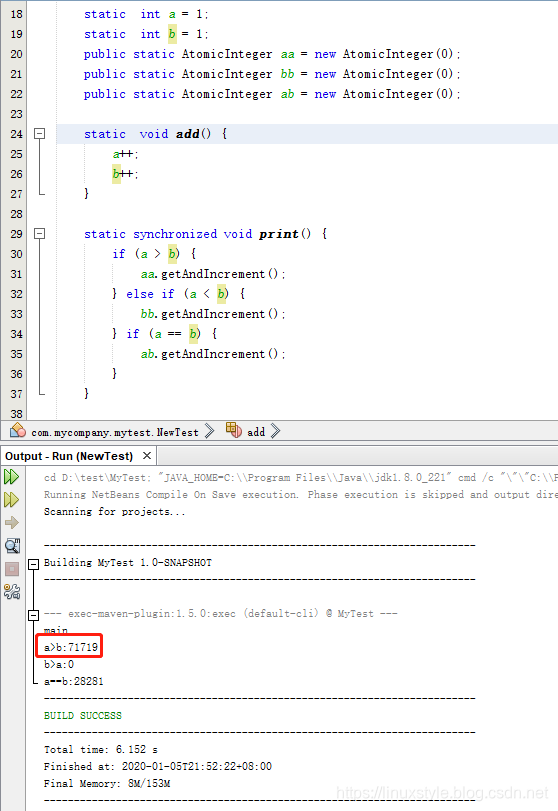
你真的掌握了并发编程volatile synchronized么?
先看代码: import java.util.concurrent.atomic.AtomicInteger;/**** author xialuomantian*/ public class NewTest {static volatile int a 1;static volatile int b 1;//static int a 1;//static int b 1;public static AtomicInteger aa new AtomicInteg…

SQLSERVER存储过程基本语法使用
一、定义变量 --简单赋值 declare a int set a5 print a --使用select语句赋值 declare user1 nvarchar(50) select user1张三 print user1 declare user2 nvarchar(50) select user2 Name from ST_User where ID1 print user2 --使用update语句赋值 declare user3 nv…

线上java JVM问题排查
作者:霞落满天 第一部分 是我以前公司的一则正式案例: 第二部分 是我另一个博客上写的主要是最近发现大家问的比较多就写了此文 第一部分 线上真实故障案例 下面是一个老系统,代码写的有点问题导致出现这样一个JVM占比过高的问题ÿ…

走向云时代的大型机
大型机,又称大型主机,英文名mainframe,是指使用专用的处理器指令集、操作系统和应用软件的有机整体。大型机最早诞生于上个世纪六十年代,经过四十多年的不断发展,其在可靠性、安全性、可用性和灵活性方面首屈一指。近年…

区分 欧几里得距离 曼哈坦距离 明考斯基距离
欧几里德距离(Euclidean Distance),欧氏距离。一种通常采用的表示相似度的距离定义,是表示在m维空间中两个点之间的真实距离。 对于n维空间中的两个点之间的欧几里得距离d(i,j)表示为: d(i,j) (|xi1-xj1|2|xi2-xj2|2……|xip-xjp|2)1/2 当n2…

传统行业转型微服务的挖坑与填坑
原文:传统行业转型微服务的挖坑与填坑一、微服务落地是一个复杂问题,牵扯到IT架构,应用架构,组织架构多个方面 在多家传统行业的企业走访和落地了微服务之后,发现落地微服务是一个非常复杂的问题,甚至都不完全是技术问…

Windows下安装Mongodb SpringBoot集成MongoDB和Redis多数据源
全文内容: Mongodb安装 说明:Mongodb和redis是开发中常用的中间件,Redis的安装使用比较简单就不写了,只说本地也就是Windows安装Mongodb。 SpringBoot集成MongoDB和Redis 文中还有一个彩蛋Hutool 1.下载最新稳定版 https://w…

使用CSDN-markdown编辑器
欢迎使用Markdown编辑器写博客 本Markdown编辑器使用StackEdit修改而来,用它写博客,将会带来全新的体验哦: Markdown和扩展Markdown简洁的语法代码块高亮图片链接和图片上传LaTex数学公式UML序列图和流程图离线写博客导入导出Markdown文件丰…

HTTP缓存相关头
本文说的是HTTP中控制客户端缓存的头有哪些。网上这方面的文章很多了,这里就说下个人的理解。 在请求一个静态文件的时候(图片,css,js)等,这些文件的特点是文件不经常变化,将这些不经常变化的文…

Thrift RPC 系列教程(4)——源码目录结构组织
Thrift 代码就是编程代码。是代码,就应该有良好的工程组织,并且,单独git仓库、版本管理,都是必不可少的。 前面我们简单总结了一些 Thrift 的一些基础知识点,但无非是一些细节层面的东西,所谓『细枝末节』也…

Spring Bean四种注入方式(Springboot环境)
阅读此文建议参考本人写的Spring常用注解:https://blog.csdn.net/21aspnet/article/details/104042826 给容器中注册组件的四种方法: 1.ComponentScan包扫描组件标注注解Component(ControllerServiceRepository) 使用场景:自己写的代码&…

chrome dev debug network 的timeline说明
在使用chrome的时候F12的开发者工具中有个network,其中对每个请求有个timeline的说明,当鼠标放上去会有下面的显示: 这里面的几个指标在说明在chrome使用文档有说明: 下面我用人类的语言理解下: Proxy 与代理服务器的连…
