证明实对称正定矩阵A的Gauss-Seidel法必定收敛(完整过程)
Solution:
\quad将nnn阶实对称矩阵AAA设为D−L−LTD-L-L^TD−L−LT,其中DDD是AAA的所有主对角元素构成对角矩阵,−L-L−L是AAA的所有主对角线以下的元素构成的严格下三角矩阵。
\quad此时Gauss−SeidelGauss-SeidelGauss−Seidel法的迭代矩阵为(D−L)−1LT(D-L)^{-1}L^T(D−L)−1LT,设其特征值为λ\lambdaλ,则有(D−L)−1LTx=λx(D-L)^{-1}L^Tx=\lambda x(D−L)−1LTx=λx,即LTx=λ(D−L)xL^Tx=\lambda (D-L)xLTx=λ(D−L)x,两边同乘xTx^TxT,有xTLTx=λxT(D−L)xx^TL^Tx=\lambda x^T(D-L)xxTLTx=λxT(D−L)x,设xTLTx=p−qix^TL^Tx=p-qixTLTx=p−qi,两边取转置有xLxT=p+qixLx^T=p+qixLxT=p+qi。
\quad于是xTAx=xT(D−L−LT)x=xTDx−xT(L+LT)x=xTDx−2px^TAx=x^T(D-L-L^T)x=x^TDx-x^T(L+L^T)x=x^TDx-2pxTAx=xT(D−L−LT)x=xTDx−xT(L+LT)x=xTDx−2p。
\quadAAA的特征值λ=xTLTxxT(D−L)x=p−qixTDx−xTLx=p−qixTDx−p−qi\lambda=\frac{x^TL^Tx}{x^T(D-L)x}=\frac{p-qi}{x^TDx-x^TLx}=\frac{p-qi}{x^TDx-p-qi}λ=xT(D−L)xxTLTx=xTDx−xTLxp−qi=xTDx−p−qip−qi,由于DDD是正定矩阵,所以有∣λ∣2=λ⋅λˉ=p2+q2(xTDx−p)2+q2|\lambda|^2=\lambda\cdot\bar{\lambda}=\frac{p^2+q^2}{(x^TDx-p)^2+q^2}∣λ∣2=λ⋅λˉ=(xTDx−p)2+q2p2+q2。
\quad又因为AAA是正定矩阵,所以xTAx=xTDx−2p>0x^TAx=x^TDx-2p\gt0xTAx=xTDx−2p>0,即xTDx−p>px^TDx-p\gt pxTDx−p>p。
\quad所以∣λ∣2=p2+q2(xTDx−p)2+q2<p2+q2p2+q2=1|\lambda|^2=\frac{p^2+q^2}{(x^TDx-p)^2+q^2}\lt\frac{p^2+q^2}{p^2+q^2}=1∣λ∣2=(xTDx−p)2+q2p2+q2<p2+q2p2+q2=1,λ<1\lambda<1λ<1。
\quad谱半径ρ=max1≤i≤nλ<1\rho=max_{1\le i\le n}{\lambda}\lt1ρ=max1≤i≤nλ<1,Gauss−SeidelGauss-SeidelGauss−Seidel法收敛。
相关文章:

5月中旬的一些总结
考完英语口语了,最大的帮助就是找到了练习的方法和思路。 周三晚上有谷歌的全球IO大会。 ******** 写吴斌老师的课程作业,这才发现winedt过期了。用了rept之后本来是解决问题了,可是一联网就又不行了。总要关上再打开。用防火墙阻断却找不到选…

项目总结10:通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题...
通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题 关键字 springboot热部署 ClassCastException异常 反射 redis 前言 最近项目出现一个很有意思的问题,用户信息(token)储存在redis中;在获取token,反序列…

Rouche Theorem(Stein复分析)
Rouche Theorem: \quadIffandgareholomorphicfunctionsinaregionΩcontainingacircleCanditsinterior,and∣f(z)∣≥∣g(z)∣forz∈C,fandfghavethesamenumbersofzerosinsidethecircleC.If\quad f\quad and\quad g\quad are\quad holomorphic\quad functions\quad i…

Java线上程序频繁JVM FGC问题排障与启示
线上Java程序的JVM频繁FGC,现象如图所示: 一直持续FGC 5次左右,每次耗时1秒多不等。 FGC的原因实际上是内存不够用,但是运维反映堆内存是2G,从运维提供的参数看也是。 内存实际上一直只用到1G以内。 这时候可以自己写…

python常用数据结构的常用操作
作为基础练习吧。列表LIST,元组TUPLE,集合SET,字符串STRING等等,显示,增删,合并。。。 #List shoplist [apple,mango,carrot,banana] print I have ,len(shoplist), items to purchase. print These items are: for …

h5 和native 交互那些事儿
前端菜菜一枚,写下关于h5 和native 交互那些事情。偏前端,各种理论知识,不在赘述。之前有各位大牛已经写过。我只写代码,有问题,下面留言/* 关于h5 和native 之间的交互 JSBridge 解决问题,偏向前端* 使用U…

手把手教你写电商爬虫-第二课 实战尚妆网分页商品采集爬虫
系列教程 手把手教你写电商爬虫-第一课 找个软柿子捏捏 如果没有看过第一课的朋友,请先移步第一课,第一课讲了一些基础性的东西,通过软柿子"切糕王子"这个电商网站好好的练了一次手,相信大家都应该对写爬虫的流程有了一…

Python程序设计 第六章 函数(续
复习 1. 10进制 ⇒\Rightarrow⇒ 2进制 除2取余,从低位到高位存储到字符串中,从高位到低位def d2b(n):if n>1:d2b(n//2)print(n%2,end)d2b(4)出口: 条件,值确定 (一)return (二)函数体执行结…

K8S的横向自动扩容的功能Horizontal Pod Autoscaling
K8S 作为一个集群式的管理软件,自动化、智能化是免不了的功能。Google 在 K8S v1.1 版本中就加入了这个 Pod 横向自动扩容的功能(Horizontal Pod Autoscaling,简称 HPA)。 HPA 与之前的 Deployment、Service 一样,也属…
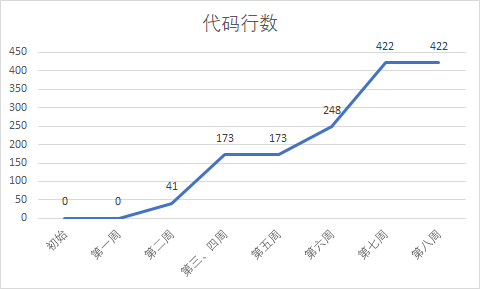
第八周例行报告
此作业要求参见:https://edu.cnblogs.com/campus/nenu/2018fall/homework/2326 1、本周PSP 类型 任务 开始时间 结束时间 中断时间 Delta时间 会议 事后诸葛亮会议 11.3 14:12 11.3 15:08 0min 56min 博客 编写博客《事后诸葛…

HTTP头部信息解释分析(详细整理)
这篇文章为大家介绍了HTTP头部信息,中英文对比分析,还是比较全面的,若大家在使用过程中遇到不了解的,可以适当参考下 HTTP 头部解释 1. Accept:告诉WEB服务器自己接受什么介质类型,*/* 表示任何类型&#…

深圳杯---深圳市生活垃圾处理社会总成本分析
2017年3月18日,国务院向全国发布了《生活垃圾分类制度实施方案》,这标志着中国垃圾分类制度建设开始了一个全新阶段,垃圾分类已成为推进社会经济绿色发展、提升城市管理和服务水平、优化人居环境的重要举措。为了保证这一目标能够顺利实现&am…
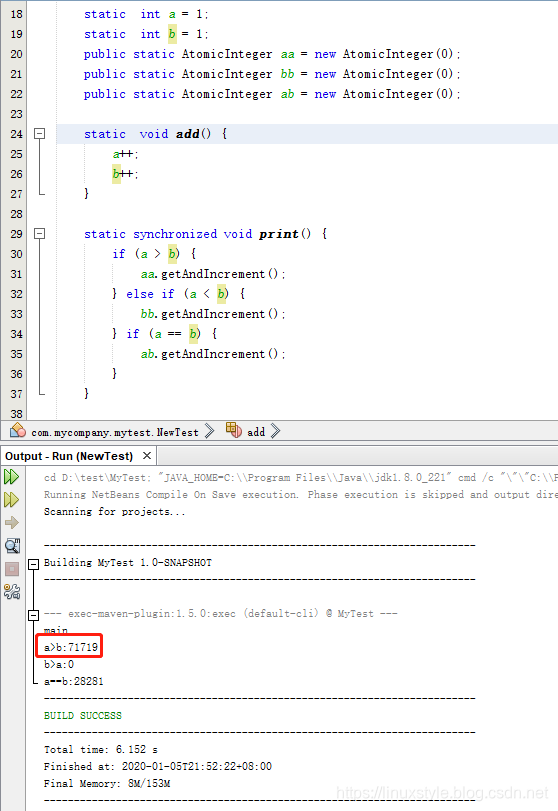
你真的掌握了并发编程volatile synchronized么?
先看代码: import java.util.concurrent.atomic.AtomicInteger;/**** author xialuomantian*/ public class NewTest {static volatile int a 1;static volatile int b 1;//static int a 1;//static int b 1;public static AtomicInteger aa new AtomicInteg…

SQLSERVER存储过程基本语法使用
一、定义变量 --简单赋值 declare a int set a5 print a --使用select语句赋值 declare user1 nvarchar(50) select user1张三 print user1 declare user2 nvarchar(50) select user2 Name from ST_User where ID1 print user2 --使用update语句赋值 declare user3 nv…

线上java JVM问题排查
作者:霞落满天 第一部分 是我以前公司的一则正式案例: 第二部分 是我另一个博客上写的主要是最近发现大家问的比较多就写了此文 第一部分 线上真实故障案例 下面是一个老系统,代码写的有点问题导致出现这样一个JVM占比过高的问题ÿ…

走向云时代的大型机
大型机,又称大型主机,英文名mainframe,是指使用专用的处理器指令集、操作系统和应用软件的有机整体。大型机最早诞生于上个世纪六十年代,经过四十多年的不断发展,其在可靠性、安全性、可用性和灵活性方面首屈一指。近年…

区分 欧几里得距离 曼哈坦距离 明考斯基距离
欧几里德距离(Euclidean Distance),欧氏距离。一种通常采用的表示相似度的距离定义,是表示在m维空间中两个点之间的真实距离。 对于n维空间中的两个点之间的欧几里得距离d(i,j)表示为: d(i,j) (|xi1-xj1|2|xi2-xj2|2……|xip-xjp|2)1/2 当n2…

传统行业转型微服务的挖坑与填坑
原文:传统行业转型微服务的挖坑与填坑一、微服务落地是一个复杂问题,牵扯到IT架构,应用架构,组织架构多个方面 在多家传统行业的企业走访和落地了微服务之后,发现落地微服务是一个非常复杂的问题,甚至都不完全是技术问…

Windows下安装Mongodb SpringBoot集成MongoDB和Redis多数据源
全文内容: Mongodb安装 说明:Mongodb和redis是开发中常用的中间件,Redis的安装使用比较简单就不写了,只说本地也就是Windows安装Mongodb。 SpringBoot集成MongoDB和Redis 文中还有一个彩蛋Hutool 1.下载最新稳定版 https://w…

使用CSDN-markdown编辑器
欢迎使用Markdown编辑器写博客 本Markdown编辑器使用StackEdit修改而来,用它写博客,将会带来全新的体验哦: Markdown和扩展Markdown简洁的语法代码块高亮图片链接和图片上传LaTex数学公式UML序列图和流程图离线写博客导入导出Markdown文件丰…

HTTP缓存相关头
本文说的是HTTP中控制客户端缓存的头有哪些。网上这方面的文章很多了,这里就说下个人的理解。 在请求一个静态文件的时候(图片,css,js)等,这些文件的特点是文件不经常变化,将这些不经常变化的文…

Thrift RPC 系列教程(4)——源码目录结构组织
Thrift 代码就是编程代码。是代码,就应该有良好的工程组织,并且,单独git仓库、版本管理,都是必不可少的。 前面我们简单总结了一些 Thrift 的一些基础知识点,但无非是一些细节层面的东西,所谓『细枝末节』也…

Spring Bean四种注入方式(Springboot环境)
阅读此文建议参考本人写的Spring常用注解:https://blog.csdn.net/21aspnet/article/details/104042826 给容器中注册组件的四种方法: 1.ComponentScan包扫描组件标注注解Component(ControllerServiceRepository) 使用场景:自己写的代码&…

chrome dev debug network 的timeline说明
在使用chrome的时候F12的开发者工具中有个network,其中对每个请求有个timeline的说明,当鼠标放上去会有下面的显示: 这里面的几个指标在说明在chrome使用文档有说明: 下面我用人类的语言理解下: Proxy 与代理服务器的连…

【MATLAB】函数句柄
在MATLAB平台中,对函数的调用方法分为直接调用法和间接调用法。 1、直接调用函数,被调用的函数通常称为子函数。一个文件中只能有一个主函数。 2、函数句柄——提供一种间接调用函数的方法。创建函数句柄需要用到操作符。 创建函数句柄的一般句法格式…
为什么企业选择年底裁员?如何选择一个正确的公司!
为什么很多企业选择年底裁员?首先分析一下裁员的原因:1、你能力不行,在公司吃闲饭2、减少公司成本3、公司换血,需要新的人才注入普通情况下,这些因素裁员很正常,只能怪自己不争气,成为末尾被淘汰…

springboot集成logback日志 通用logback.xml模板详解
先看Spring Boot中依赖的logback,log4j,slf4j相关Jar包 1.最简单的默认打印控制台日志 import org.slf4j.Logger; import org.slf4j.LoggerFactory; import org.springframework.beans.factory.annotation.Autowired; import org.springframework.web.bind.annotation.Reques…

【MATLAB】单元数组类型
1、概述 单元(Cell)数组是一种无所不包的广义数组。 组成单元数组的每个元素成为一个单元。 每一个单元可以包括任意数组,如数值数组,字符串数组,结构体数组或另外一个单元数组。 单元数组用花括号来创建“{ }”。…

UNITY3D拓展编辑器 - 目录
前文:最近在自学UNITY3D拓展器,对以上功能点做一些认知范围内的总结.目录:1. 属性编辑器http://weizeteng.blog.51cto.com/5604545/17744312. 工具编辑器3. 场景编辑器转载于:https://blog.51cto.com/weizeteng/1774390

程序员的你还沉浸在大公司就是螺丝钉?小公司锻炼人?错了!看完即懂
刚毕业那会经历过很多所谓创业公司,和很多朋友经历过画大饼,洗脑以及公司上市原始股这样的承诺。当你正在趟过这些谎言你就会发现,在这个世界上能信这些鬼话的也只有涉世未深的毕业生了。小公司里真的就是十几二十几个精英带你一路向前&#…
