Prometheus 对比 Zabbix

公司要上监控,Prometheus 是最热门的监控解决方案,作为喜新厌旧的程序员,我当然是选择跟风了,但上级更倾向于 Zabbix,那没办法,只能好好对比一番,给出几个靠谱的理由了。
但稍稍深入一点,我就体会到,我之前其实并没有真的理解口口相传的 Prometheus 的优点,这次对比虽然是始于无奈,但还是蛮有意义的,正好总结一下自己粗浅的体会。
1. 对比
先对两者的各自特点进行一下对比:
| Zabbix | Prometheus |
|---|---|
| 后端用 C 开发,界面用 PHP 开发,定制化难度很高。 | 后端用 golang 开发,前端是 Grafana,JSON 编辑即可解决。定制化难度较低。 |
| 集群规模上限为 10000 个节点。 | 支持更大的集群规模,速度也更快。 |
| 更适合监控物理机环境。 | 更适合云环境的监控,对 OpenStack,Kubernetes 有更好的集成。 |
| 监控数据存储在关系型数据库内,如 MySQL,很难从现有数据中扩展维度。 | 监控数据存储在基于时间序列的数据库内,便于对已有数据进行新的聚合。 |
| 安装简单,zabbix-server 一个软件包中包括了所有的服务端功能。 | 安装相对复杂,监控、告警和界面都分属于不同的组件。 |
| 图形化界面比较成熟,界面上基本上能完成全部的配置操作。 | 界面相对较弱,很多配置需要修改配置文件。 |
| 发展时间更长,对于很多监控场景,都有现成的解决方案。 | 2015 年后开始快速发展,但发展时间较短,成熟度不及 Zabbix。 |
2. 解析
更进一步的分析两者的主要差异:
2.1 图形化还是配置文件
Zabbix 的图形化配置毫无疑问是完爆 Prometheus 的,但这真的是个优势吗?
细想起来还真未必。图形化确实省去了手动改配置文件和命令行的繁琐,但这种努力毫无疑问是已经做出了需要人工介入的假设。但 Prometheus 是为云原生环境而生的,这种情况下,环境是动态变化的,服务器会随时增减,人工介入不太现实,那么图形化在这种情况下意义就不大了,毕竟要做自动化,那就不必要过图形界面这一道了。这么看来 Prometheus 在图形化方面的简约也是有意的取舍。
2.2 时序数据库还是关系型数据
近几年兴起的监控系统大部分都选择了将数据存储在时序型数据库中,Prometheus 用的就是自研的 TSDB,Zabbix 则用的是 MySQL 或 PostgreSQL。对于时序型数据库我了解不多,粗浅的来看,Prometheus 的时序型数据库在高并发的情况下,读写性能是远高过传统的关系型数据库的,另外还提供了很多内置的基于时间的处理函数,简化数据聚合的难度。也许这不能简单的理解为两种数据库的特性造成的结果,但至少说明,对专门监控场景进行存储优化,是十分必要的。
2.3 服务发现
大家都知道 Prometheus 在收集数据时,采用的 Pull 模型(服务端主动去客户端拉取数据),而以 Zabbix 为代表的传统监控采用的 Push 模型(客户端发送数据给服务端)。Pull 模型在云原生环境中有比较大的优势,原因是分布式系统中,一定是有中心节点知道整个集群信息的,那么通过中心节点就可以完成所有要监控节点的服务发现,去拉取数据就好了;Push 模型倒是省去了服务发现的步骤,但每个被监控的服务都需要内置客户端,还需要配置监控服务端的信息,这加大了部署的难度,Push 模型在 OpenStack 和 Kubernetes 等环境中用的不多。
2.4 开发语言
Golang 和 C 语言的开发对比,这就不用多解释了,不是一个时代的语言,Golang 占绝对优势。PHP 写界面倒是很常规的选择,但无奈 Grafana 写界面都不用编程语言,JSON 和 YAML 就可以搞定。所以真的要做定制开发,Prometheus 的难度要小很多。
3. 总结
Zabbix 的成熟度更高,上手更快,但更好的集成导致灵活性较差,问题更大是,监控数据的复杂度增加后,Zabbix 做进一步定制难度很高,即使做好了定制,也没法利用之前收集到的数据了(关系型数据库造成的问题)。
Prometheus 基本上是正相反,上手难度大一些,但由于定制灵活度高,数据也有更多的聚合可能,起步后的使用难度远小于 Zabbix。
比较一番下来,我的建议是,如果是刚刚要上监控系统的话,不用犹豫了,Prometheus 准没错。
但如果已经对传统监控系统有技术积累的话,还是要谨慎考虑:如果监控的是物理机,用 Zabbix 没毛病,或者是环境变动不会很频繁的情况下,Zabbix 也会比 Prometheus 好使;但如果是云环境的话,除非是 Zabbix 玩的非常溜,可以做各种定制,那还是 Prometheus 吧,毕竟人家就是干这个的。
4. 参考文档
- What's the difference between Prometheus and Zabbix?
- Prometheus vs Zabbix
- Zabbix vs Prometheus
- What's the difference between Prometheus and Zabbix?
相关文章:

好理解的Java内存虚假共享(False Sharing)性能损耗以及解决方案
虚假共享(False Sharing)也有人翻译为伪共享 参考 https://en.wikipedia.org/wiki/False_sharing 在计算机科学中,虚假共享是一种性能降低的使用模式,它可能出现在具有由高速缓存机制管理的最小资源块大小的分布式一致高速缓存的系统中。当系统参与者将…

delphi xe 文件服务器,DelphiXE7中创建WebService(服务端+客户端)
相关资料:http://www.2ccc.com/news/Html/?1507.htmlhttp://www.dfwlt.com/forum.php?modviewthread&tid922DelphiXE7新建WebService具体操作:1.打开“DelphiXE7”->“File”->“New”->“Other”2.“New Items”->“Delph…

Android app 别用中文名
/************************************************************************** Android app 别用中文名* 说明:* 本来想分析一下这份源代码,结果发现因为项目名中有中文不能自动生成R* 文件,于是不想分析了。** …
一线互联网常见的14个Java面试题,你颤抖了吗程序员
跳槽不算频繁,但参加过不少面试(电话面试、face to face面试),面过大/小公司、互联网/传统软件公司,面糊过(眼高手低,缺乏实战经验,挂掉),也面过人࿰…

复化梯形公式,Newton-Cotes公式,变量代换后的复化梯形公式,Gauss-Legendre公式,Gauss-Jacobi公式插值积分的精确度比较
1.问题 分别计算积分 Ic∫01cosxxdx1.809048475800...I_c\int_0^1\frac{\cos{x}}{\sqrt{x}}dx1.809048475800... Ic∫01xcosxdx1.809048475800... Is∫01sinxxdx0.620536603446I_s\int_0^1\frac{\sin{x}}{\sqrt{x}}dx0.620536603446 Is∫01xsinxdx0.62053…

Elasticsearch 知识点目录
2019独角兽企业重金招聘Python工程师标准>>> 经过一段时间的编写,完成了第一个版本的Elasticsearch书籍的编写,目录结构如下: 1 Elasticsearch入门 7 1.1 Elasticsearch是什么 7 1.1.1 Elasticsearch是什么 7 1.1.2 Elasticsearch…

不要千言万语,一组漫画让你秒懂最终一致性
直接上图 如果你以前看过最终一致性的定义那么你一定会为这幅精彩漫画拍手叫好。 你要是不知道什么是最终一致性你可以看看下面的权威定义,当然了网上关于什么是最终一致性的帖子铺天盖地,也许你已经很明白了,即使这样你是不是依然为此图欢呼…

Feign实现服务调用
上一篇博客我们使用ribbonrestTemplate实现负载均衡调用服务,接下来我们使用feign实现服务的调用,首先feign和ribbon的区别是什么呢? ribbon根据特定算法,从服务列表中选取一个要访问的服务; RoundRobinRule:轮询RandomRule:随机Availability…

度量,跟踪和日志记录
今天,我有幸参加了2017年的分布式追踪峰会,其中有很多来自AWS / X-Ray,OpenZipkin,OpenTracing,Instana,Datadog,Librato等公司的人员,我很遗憾我忘记了这一点。有一次讨论转向了项目…

python 第六章 函数 pta(1)
1.Multiple-Choice 1.print(type(lambda:3))的输出结果是____。 A.<class ‘function’> B.<class ‘int’> C.<class ‘NoneType’> D.<class ‘float’> 答案:A 2.在Python中,对于函数定义代码的理解,正确的理解…
生成.a文件步骤
1.新建一个Project 选择 iOS->Framework & Library ->Cocoa Touch Static Library点击Next-> 输入Product Name 2.删除自动生成的文件 替换成我们需要的文件 如:原本自定生成的文件为继承自NSObject的,而你需要的为继承自UIView的ÿ…
机器学习之优雅落地线性回归法
在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析维基百科。简单线性回归当只有一个自变量的时候,成为简单线性回归。简单线性回归模型的思…
SpringBoot整合Grpc实现跨语言RPC通讯
什么是gRPC gRPC是谷歌开源的基于go语言的一个现代的开源高性能RPC框架,可以在任何环境中运行。它可以有效地连接数据中心内和跨数据中心的服务,并提供可插拔的支持,以实现负载平衡,跟踪,健康检查和身份验证。它还适用…

python 第六章 函数
1.函数的定义 def 名称(形参): 函数体 2.函数的调用 名称(实参) 单独文件:模块 调用方式——模块.名称 3.函数的参数类型 1.位置参数: def add(a,b):add(2,3) #顺序,个数,数据类型都要相同!!…
C++简单使用Jsoncpp来读取写入json文件
一、源码编译 C操作json字符串最好的库应该就是jsoncpp了,开源并且跨平台。它可以从这里下载。 下载后将其解压到任意目录,它默认提供VS2003和VS2010的工程文件,使用VS2010可以直接打开makefiles\msvc2010目录下的sln文件。 工程文件提供Json…

BZOJ 3420: Poi2013 Triumphal arch
二分答案 第二个人不会走回头路 那么F[i]表示在i的子树内(不包括i)所需要的额外步数 F[1]0表示mid可行 k可能为0 #include<cstdio> #include<algorithm> using namespace std; int cnt,n,mid,F[300005],last[300005]; struct node{int to,next; }e[600005]; void a…
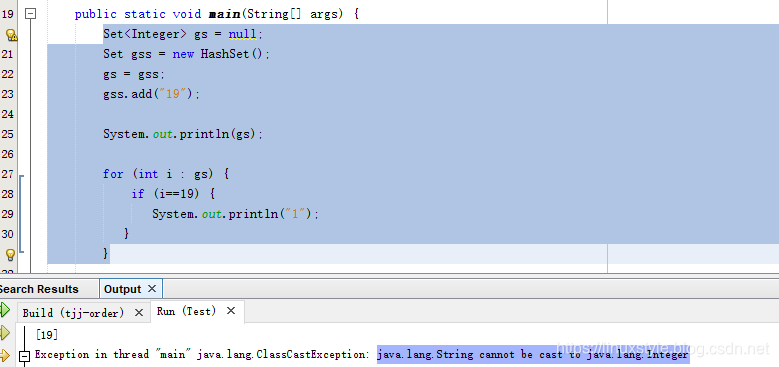
Java泛型使用需要小心
这是源自实际开发的一个坑,只是被我简化了。 Set<Integer> gs null;Set gss new HashSet();gs gss;gss.add("19");System.out.println(gs);for (int i : gs) {if (i19) {System.out.println("1");}} 代码经过一些转换你如果不注意以…

证明实对称正定矩阵A的Gauss-Seidel法必定收敛(完整过程)
Solution: \quad将nnn阶实对称矩阵AAA设为D−L−LTD-L-L^TD−L−LT,其中DDD是AAA的所有主对角元素构成对角矩阵,−L-L−L是AAA的所有主对角线以下的元素构成的严格下三角矩阵。 \quad此时Gauss−SeidelGauss-SeidelGauss−Seidel法的迭代矩阵为(D−L)−1LT(…

5月中旬的一些总结
考完英语口语了,最大的帮助就是找到了练习的方法和思路。 周三晚上有谷歌的全球IO大会。 ******** 写吴斌老师的课程作业,这才发现winedt过期了。用了rept之后本来是解决问题了,可是一联网就又不行了。总要关上再打开。用防火墙阻断却找不到选…

项目总结10:通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题...
通过反射解决springboot环境下从redis取缓存进行转换时出现ClassCastException异常问题 关键字 springboot热部署 ClassCastException异常 反射 redis 前言 最近项目出现一个很有意思的问题,用户信息(token)储存在redis中;在获取token,反序列…

Rouche Theorem(Stein复分析)
Rouche Theorem: \quadIffandgareholomorphicfunctionsinaregionΩcontainingacircleCanditsinterior,and∣f(z)∣≥∣g(z)∣forz∈C,fandfghavethesamenumbersofzerosinsidethecircleC.If\quad f\quad and\quad g\quad are\quad holomorphic\quad functions\quad i…

Java线上程序频繁JVM FGC问题排障与启示
线上Java程序的JVM频繁FGC,现象如图所示: 一直持续FGC 5次左右,每次耗时1秒多不等。 FGC的原因实际上是内存不够用,但是运维反映堆内存是2G,从运维提供的参数看也是。 内存实际上一直只用到1G以内。 这时候可以自己写…

python常用数据结构的常用操作
作为基础练习吧。列表LIST,元组TUPLE,集合SET,字符串STRING等等,显示,增删,合并。。。 #List shoplist [apple,mango,carrot,banana] print I have ,len(shoplist), items to purchase. print These items are: for …

h5 和native 交互那些事儿
前端菜菜一枚,写下关于h5 和native 交互那些事情。偏前端,各种理论知识,不在赘述。之前有各位大牛已经写过。我只写代码,有问题,下面留言/* 关于h5 和native 之间的交互 JSBridge 解决问题,偏向前端* 使用U…

手把手教你写电商爬虫-第二课 实战尚妆网分页商品采集爬虫
系列教程 手把手教你写电商爬虫-第一课 找个软柿子捏捏 如果没有看过第一课的朋友,请先移步第一课,第一课讲了一些基础性的东西,通过软柿子"切糕王子"这个电商网站好好的练了一次手,相信大家都应该对写爬虫的流程有了一…

Python程序设计 第六章 函数(续
复习 1. 10进制 ⇒\Rightarrow⇒ 2进制 除2取余,从低位到高位存储到字符串中,从高位到低位def d2b(n):if n>1:d2b(n//2)print(n%2,end)d2b(4)出口: 条件,值确定 (一)return (二)函数体执行结…

K8S的横向自动扩容的功能Horizontal Pod Autoscaling
K8S 作为一个集群式的管理软件,自动化、智能化是免不了的功能。Google 在 K8S v1.1 版本中就加入了这个 Pod 横向自动扩容的功能(Horizontal Pod Autoscaling,简称 HPA)。 HPA 与之前的 Deployment、Service 一样,也属…
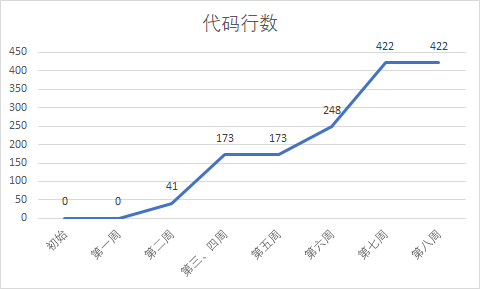
第八周例行报告
此作业要求参见:https://edu.cnblogs.com/campus/nenu/2018fall/homework/2326 1、本周PSP 类型 任务 开始时间 结束时间 中断时间 Delta时间 会议 事后诸葛亮会议 11.3 14:12 11.3 15:08 0min 56min 博客 编写博客《事后诸葛…

HTTP头部信息解释分析(详细整理)
这篇文章为大家介绍了HTTP头部信息,中英文对比分析,还是比较全面的,若大家在使用过程中遇到不了解的,可以适当参考下 HTTP 头部解释 1. Accept:告诉WEB服务器自己接受什么介质类型,*/* 表示任何类型&#…

深圳杯---深圳市生活垃圾处理社会总成本分析
2017年3月18日,国务院向全国发布了《生活垃圾分类制度实施方案》,这标志着中国垃圾分类制度建设开始了一个全新阶段,垃圾分类已成为推进社会经济绿色发展、提升城市管理和服务水平、优化人居环境的重要举措。为了保证这一目标能够顺利实现&am…
