【MATLAB】稀疏矩阵(含有大量0元素的矩阵)
1、稀疏矩阵的储存方式
对于稀疏矩阵,MATLAB仅储存矩阵所有非零元素的值及其位置(行号和列号)。
2、稀疏矩阵的生成
1)利用sparse函数从满矩阵转换得到稀疏矩阵
| 函数名称 | 表示意义 |
| sparse(A) | 由非零元素和下标建立稀疏矩阵A。如果A已是一个稀疏矩阵,则返回A本身。 |
| sparse(u,v,a) | 生成大小为max(u) x max(v)的稀疏矩阵。其中u和v是整数向量,a是实数或者复数向量 |
| sparse(u,v,a,m,n) | 生成m x n 的一个稀疏矩阵,(ui,vi)对应值ai,向量u,v和a的长度必须一样 |
| spconvert(D) | 生成一个稀疏矩阵D。D共有三列,第一列为行下表,第二列为列下表,第三列为元素值 |
| full(S) | 将稀疏矩阵S转换为满矩阵 |
>> clear all
>> x=[1 2 3]x =1 2 3>> y=[4 5 6]y =4 5 6>> sparse(x,y,7)ans =(1,4) 7(2,5) 7(3,6) 7>> S=sparse([1,2,3,4,5],[2,1,4,6,2],[10,3,-2,-5,1],10,12)S =(2,1) 3(1,2) 10(5,2) 1(3,4) -2(4,6) -5>> A=full(S)A =0 10 0 0 0 0 0 0 0 0 0 03 0 0 0 0 0 0 0 0 0 0 00 0 0 -2 0 0 0 0 0 0 0 00 0 0 0 0 -5 0 0 0 0 0 00 1 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0nnz(S):查看非零元素的个数
nonzeros(S):非零元素的值
nzmax(S):获取储存非零元素的空间长度
spy(S):对稀疏矩阵的非零元素进行图形化显示
2)利用一些特定函数创建包括单位稀疏矩阵在内的特殊稀疏矩阵
| 函数 | d调用格式 | m描述 |
| speye | S=speye(m,n) | 创建单位稀疏矩阵 |
| spones | S=spones(X) | 创建非零元素为1的稀疏矩阵 |
| sprand | S=sprand(X) | 创建非零元素为均匀分布的随机数稀疏矩阵 |
| sprandn | S=sprandn(X) | 创建非零元素为高斯分布的随机数的稀疏矩阵 |
| sprandsym | S=sprandsym(X) | 创建非零元素为高斯分布的随机数的对称稀疏矩阵 |
| spdiags | S=spdiags(X) | 创建对角稀疏矩阵 |
| spalloc | spalloc(X) | 为稀疏矩阵分配空间 |
>> A=speye(5)A =(1,1) 1(2,2) 1(3,3) 1(4,4) 1(5,5) 1>> B=speye(5,6)B =(1,1) 1(2,2) 1(3,3) 1(4,4) 1(5,5) 1>> a=full(A)a =1 0 0 0 00 1 0 0 00 0 1 0 00 0 0 1 00 0 0 0 1>> b=full(B)b =1 0 0 0 0 00 1 0 0 0 00 0 1 0 0 00 0 0 1 0 00 0 0 0 1 0>> C=spones(a)C =(1,1) 1(2,2) 1(3,3) 1(4,4) 1(5,5) 1
3、稀疏矩阵的运算
满矩阵的四则运算对稀疏矩阵同样有效
对单个稀疏矩阵的输入,大部分函数输出的结果都是稀疏矩阵
对多个矩阵的输入,如果至少有一个矩阵式满矩阵,那么,大部分结果输出的是满矩阵
对矩阵的加减乘除运算,只要有一个是满矩阵,输出结果是满矩阵
稀疏矩阵的数乘是稀疏矩阵
稀疏矩阵的幂是稀疏矩阵
| c创建非零元素为高斯分布的随机数的稀疏矩阵 |
相关文章:

httpTomcat
Tomcat是web应用服务器的一种 转载于:https://juejin.im/post/5beaf7e451882517165d91d1

memcached(二)事件模型源码分析
在memcachedd中,作者为了专注于缓存的设计,使用了libevent来开发事件模型。memcachedd的时间模型同nginx的类似,拥有一个主进行(master)以及多个工作者线程(woker)。 流程图 在memcached中&…

【MATLAB】MATLAB的控制流
1、if-else-end if expressioncommands1 elseif expression2commands2 ... else commandsn end 2、switch-case switch valuecase1 test1%如果value等于test1,执行command1,并结束此结构command1case2 test2command2...case3 testkcommandk otherw…

Linux查看本机端口
查看指定的端口 # lsof -i:port 查看所有端口 # netstat -aptn 安装telnet #yum install -y telnet.x86_64 #telnet ip 端口

Node.js安装
通过nvm安装 下载nvm并执行wget -qO- https://raw.github.com/creationix/nvm/v0.33.11/install.sh | sh将命令输出到终端命令中~/.bashrcexport NVM_DIR"$HOME/.nvm"更新文件source .bashrc通过nvm安装node.jsnvm install 10.13安装的版本是10.13的版本 通过命令查看…

mongodb常用语句以及SpringBoot中使用mongodb
普通查询 某个字段匹配数组内的元素数量的,假如region只有一个元素的 db.getCollection(map).find({region:{$size:1}}) 假如region只有0个元素的 db.getCollection(map).find({region:{$size:0}}) db.getCollection(map).find({region:{$size:1}}).count() db.get…

2002高教社杯---A车灯线光源的优化设计
A题 车灯线光源的优化设计 安装在汽车头部的车灯的形状为一旋转抛物面,车灯的对称轴水平地指向正前方, 其开口半径36毫米,深度21.6毫米。经过车灯的焦点,在与对称轴相垂直的水平方向,对称地放置一定长度的均匀分布的线光源。要求…

从Date类型转为中文字符串
//主方法public static String DateToCh(Date date) {Calendar cal Calendar.getInstance();cal.setTime(date);int year cal.get(Calendar.YEAR);int month cal.get(Calendar.MONTH) 1;int day cal.get(Calendar.DAY_OF_MONTH);return getYear(year) getTenString(month…

第十四课 如何在DAPP应用实现自带钱包转账功能?
1,为什么DAPP生态需要自带钱包功能? 区块链是一个伟大的发明,它改变了生产关系。很多生态,有了区块链技术,可以由全公司员工的"全员合伙人"变成了全平台的”全体合伙人”了,是真正的共享经济模式…

为什么jdk源码推荐ThreadLocal使用static
ThreadLocal是线程私有变量,本身是解决多线程环境线程安全,可以说单线程实际上没必要使用。 既然多线程环境本身不使用static,那么又怎么会线程不安全。所以这个问题本身并不是问题,只是有人没有理解ThreadLocal的真正使用场景&a…

C与C++之间相互调用
1、导出C函数以用于C或C的项目 如果使用C语言编写的DLL,希望从中导出函数给C或C的模块访问,则应使用 __cplusplus 预处理器宏确定正在编译的语言。如果是从C语言模块使用,则用C链接声明这些函数。如果使用此技术并为DLL提供头文件,…
【MATLAB】三维图形的绘制mesh
步骤如下: (1)确定自变量x和y的取值范围和取值间隔 x x1 :dx :x2 , y y1 : dy : y2 (2)构成xoy平面上的自变量采样“格点”矩阵 ①利用格点矩阵的原理生成矩阵。 xx1:dx:x2; yy1:dy:y2; Xones(size(y))*x; Yy*o…

ORA-01919: role 'PLUSTRACE' does not exist
环境:Oracle 10g,11g.现象:在一次迁移测试中,发现有这样的角色赋权会报错不存在: SYSorcl> grant PLUSTRACE to jingyu; grant PLUSTRACE to jingyu* ERROR at line 1: ORA-01919: role PLUSTRACE does not exist 查询发现这个…

Java反射以及应用
需求:需要通过反射动态获取类的字段类型,然后做特殊处理 Java反射getDeclaredField和getField的区别 getDeclaredFiled 只能获取类本身的属性成员(包括私有、共有、保护) getField 仅能获取类(及其父类可以自己测试) public属性…

【MATLAB】雅可比矩阵jacobi matrix
参考页面: https://baike.baidu.com/item/%E9%9B%85%E5%8F%AF%E6%AF%94%E7%9F%A9%E9%98%B5/10753754?fraladdin#1 在向量微积分中,雅可比矩阵是一阶偏导数以一定方式排列成的矩阵,其行列式称为雅可比行列式。 由球坐标系到直角坐标系的转…

Laravel:使用Migrations
1、首先利用artisan创建一个可迁移的数据表模板,该命令运行后会在database/migrations目录下生成一个文件 php artisan make:migration create_fees_count_table --createfees_count 2、生成的文件包含up和down两个方法,其中up中是包含了添加表ÿ…

基于libevent和unix domain socket的本地server
https://www.pacificsimplicity.ca/blog/libevent-echo-server-tutorial 根据这一篇写一个最简单的demo。然后开始写client。 client调优 client最初的代码如下: 1 #include <sys/socket.h>2 #include <sys/un.h>3 #include <stdio.h>4 #include …
软件体系架构模式之一什么是软件架构模式
什么是软件架构模式 计划启动未开发的软件项目?然后选择正确的架构模式将对项目的结果起关键作用。选择市场上最流行或最新的技术并不总是意味着会带来最好的结果。但是,选择最合适的解决方案将为行之有效的问题和反复出现的问题提供可靠的解决方案。 …

HP 服务器 iLO 远程控制软件 介绍
iLO了解:iLO 是一组芯片,内部是vxworks的嵌入操作系统,在服务器的背后有一个标准RJ45口对外连接生产用交换机或者带外管理的交换机。iLO 全名是 Integrated Lights-out,它是惠普某些型号的服务器上集成的远程管理端口,它能够允许用…

【MATLAB】数据分析之数据插值
插值:求过已知有限个数据点的近似函数。 区别于拟合: 拟合:已知有限个数据点求近似函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最小。 基本常用的插值方法:拉格朗日多项式插值&…

迈斯!啊呸~数学
1.数论 快速幂 int po(int x,int y) {int ans1;while(y){if(y%21)ans1ll*ans*x%p;x1ll*x*x%p;y/2;}return ans; } 乘法逆元(保证模域p与求逆元的数互质) po(a,p-2);//a为需要求逆元的数 扩展欧几里得(exgcd) #include<cstdio&g…
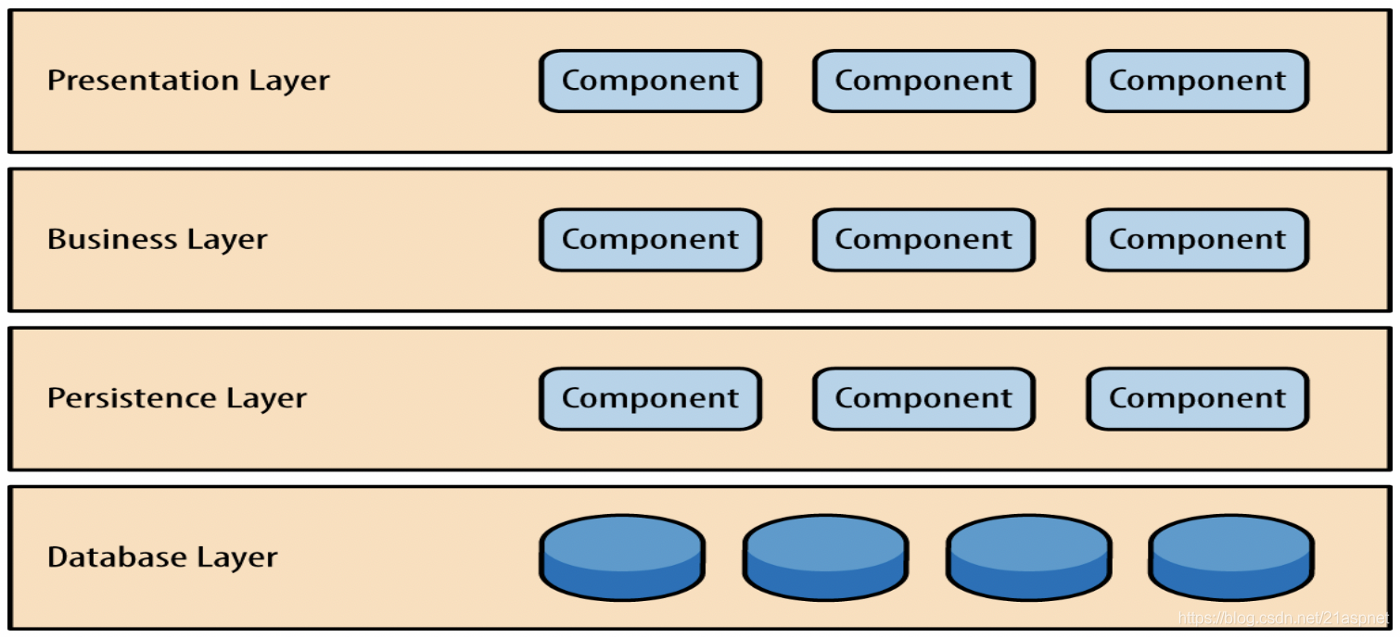
软件体系架构模式之二分层体系结构
分层体系结构模式是n层模式,其中组件被组织在水平层中。这是设计大多数软件的传统方法,并且具有独立性。这意味着所有组件都是互连的,但彼此之间不依赖。 图1:分层架构 在此体系结构中有四层,其中每一层在模块和其中的…

linux下mysql的root密码忘记解决方法
1.首先确认服务器出于安全的状态,最安全的状态是到服务器的Console上面操作,并且拔掉网线,或者可以使用--skip-networking限制只能从本地连接2.修改MySQL的登录设置: # vim /etc/my.cnf在[mysqld]的段中加上…

【Python】turtle库的小应用
心血来潮,哈哈哈,画的不好,请多见谅 大家如果想要尝试turtle库,可以借鉴: https://www.cnblogs.com/nowgood/p/turtle.html 导入库,我的pycharm里可以直接使用,哈哈哈,不行就pip…

[转]MySQL修改时区的方法小结
本文转自:https://www.cnblogs.com/mracale/p/6064447.html 这篇文章主要介绍了MySQL修改时区的方法,总结分析了三种常见的MySQL时区修改技巧,包括命令行模式、配置文件方式及代码方式,需要的朋友可以参考下 方法一:通过mysql命令行模式下动态修改 1.1 查…

swift轮播图代码
import UIKit private let CycleCellID "CycleCellID" class BannerCycleView: UIView { var layout : UICollectionViewFlowLayout! var collectionView :UICollectionView! var pageContol : UIPageControl? var cycleTimer : Timer? let timeInterval : TimeI…
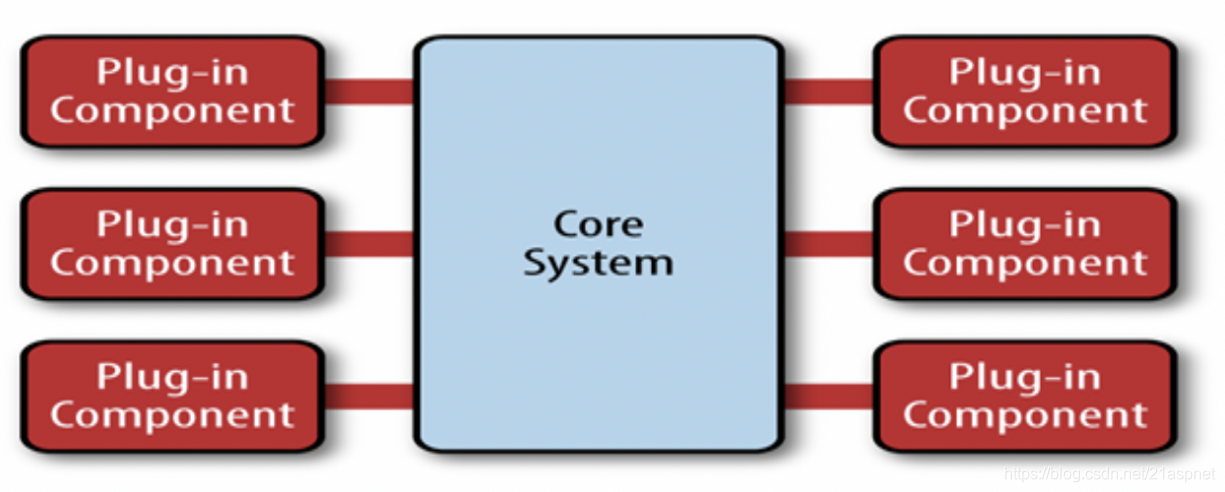
软件体系架构模式之三微内核体系架构
当您的软件系统或产品包含许多与外部实体的集成点时,微内核体系结构模式将非常有用。最重要的是,您将无法准确判断出将来将哪些实体集成到您的系统中。可以将微内核架构模式识别为基于插件的模式。。也称为插件架构模式,它由两个主要组件组成…

【MATLAB】交互式绘图(ginput,gtext,zoom)
1、ginput指令: [x,y]ginput(n) %(其功能是用鼠标从二维图形中获取n个点的数据坐标) x-8*pi:pi/100:8*pi; y1sin(x); y24*sin(x/4); plot(x,y1,r-,x,y2,k-); legend(sin(x),4sin(x/4)); grid on; [x,y]ginput(8); %在下方命令窗…

【斗医】【18】Web应用开发20天
原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 、作者信息和本声明。否则将追究法律责任。http://qingkechina.blog.51cto.com/5552198/1544928 本文通过获取首页内容来讲解Web页面拖拽获取当前页数据,功能类似在google查看图…

数据库和缓存一致性的问题
经常看到有人问怎么解决数据库和缓存一致性的问题,这个问题我觉得是不要去解决。 如果你不信你先看我列的几种情况 假设 数据库一开始和缓存都是1元。 用户更新数据库的同时双写缓存。 1.双写不删 写库充值10元>>>返回成功 ----- 时间间隔 <<<…
