软件体系架构模式之三微内核体系架构
当您的软件系统或产品包含许多与外部实体的集成点时,微内核体系结构模式将非常有用。最重要的是,您将无法准确判断出将来将哪些实体集成到您的系统中。可以将微内核架构模式识别为基于插件的模式。。也称为插件架构模式,它由两个主要组件组成,即核心系统和插件组件。
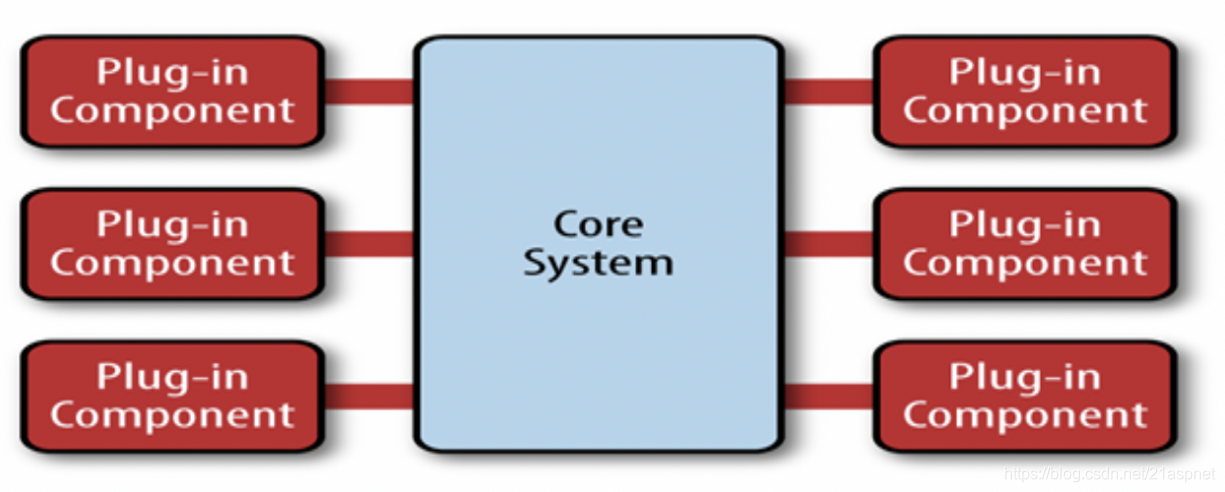
微内核架构模式的两个主要组成部分
核心系统包含运行系统所需的最少功能。在其他体系结构模式中,如果我们替换,添加或更改系统中的规则,则整个系统都会受到影响。在微内核架构中,不会发生这种情况,因为我们将规则划分为插件组件。插件模块包括其他功能,并且相互隔离且彼此独立。
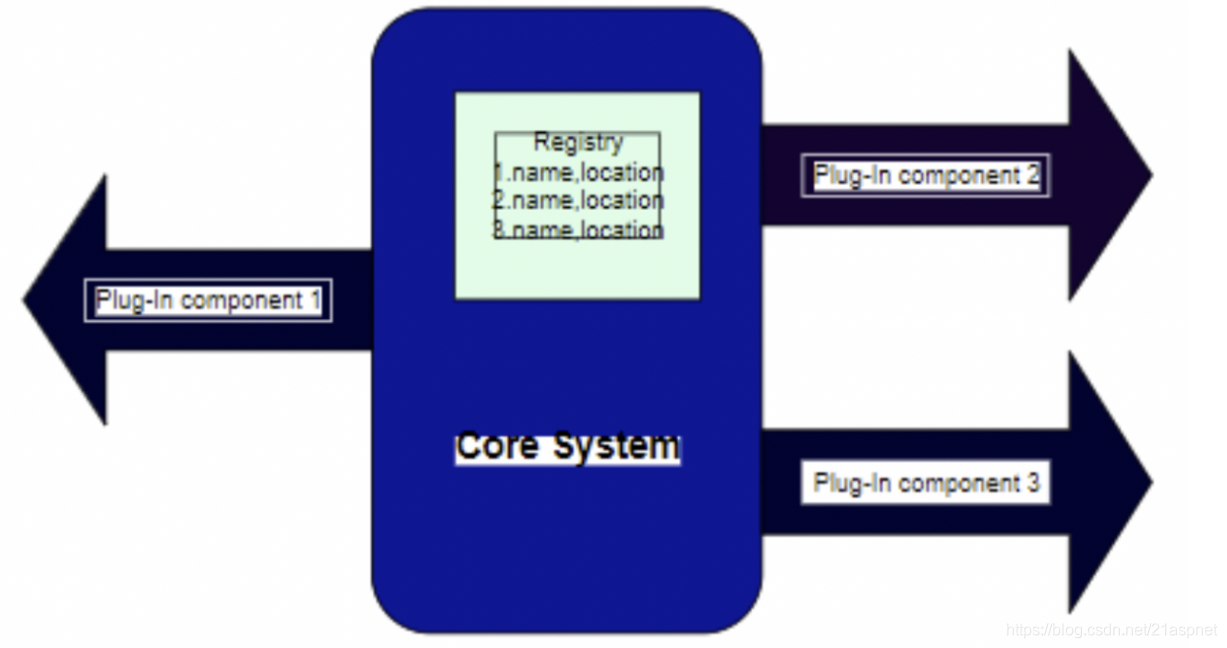
核心系统与插件的关联
核心系统需要跟踪可用的插件,因此需要通过注册表来跟踪。将组件插入核心系统时,将使用插件的名称,位置,数据协定和协定格式等信息来更新此注册表。同样,删除注册表时,注册表也会通过删除此信息进行相应更新。
合同本质上是输入和输出数据。尽管核心系统和插件可能不是同一类型,但它允许交换数据。如果使用第三方模块,而用户无法控制所使用的合同,则可以使用适配器。我们可以说明这是适配器设计模式的直接用法。这样可以确保核心系统不需要专门的代码即可读取模块。因此,插件模块仅对核心系统进行了最小的更改。这样可以轻松地测试和部署应用程序。
微内核架构模板示例
Eclipse IDE是微内核体系结构的最佳示例之一。Eclipse作为基本产品只是一个编辑器。但是,一旦添加了插件,它就会成为可定制且更有用的产品。另一个简单的示例是您使用的Web浏览器。可以添加多个插件,为基本的Web浏览器提供更多功能。
Eclipse的男女同校复习工具就是这种架构模式的一个示例。在此示例中,将有一个源验证工具(即核心系统),该工具读取Java文件并将其传递到字符串列表中并输出到报告中。在此应用程序中,所有检查组件都作为插件组件连接到核心系统。插件模块检查标头标准,拦截器,审计写等。通过源验证工具具有此类插件清单和正在运行的代码,可以轻松进行代码审查。您无需担心其他标准检查,因为它们是自动化的。
Map <String,String> pluginRegistry = new HashMap <String,String>();
静态的{
pluginRegistry.put(HEADER,“ ValidationHeaderPlugin”);
pluginRegistry.put(SQL,“ ValidationsqlPlugin”);
pluginRegistry.put(INTERCEPT,“ ValidationinterceptPlugin”);
pluginRegistry.put(AUDIT,“ ValidationAuditPlugin”);
}
这可能是注册表的样子;这只是一张简单的地图。因此,您无需使用任何外部工具即可连接到插件。
结论
以下是微内核架构模式的优缺点。
优点
它可以对插件模块中的更改做出反应,同时最大程度地减少对核心系统的更改。
与分层体系结构不同,具有插件模块意味着更易于部署,从而最大程度地减少了停机时间。
由于可以单独测试各个模块,因此测试也更加容易。
尽管通常不是用于高性能应用程序的理想模式,但由于将应用程序定制为仅包括所需的功能,因此它可以发挥良好的性能。
缺点
应用程序往往较小,因此无法高度扩展。
在实施之前需要对设计进行彻底的分析。需要分析的项目包括合同版本控制,内部插件注册表,插件粒度以及可用于插件连接的广泛选择
原文:https://medium.com/@priyalwalpita/
相关文章:

【MATLAB】交互式绘图(ginput,gtext,zoom)
1、ginput指令: [x,y]ginput(n) %(其功能是用鼠标从二维图形中获取n个点的数据坐标) x-8*pi:pi/100:8*pi; y1sin(x); y24*sin(x/4); plot(x,y1,r-,x,y2,k-); legend(sin(x),4sin(x/4)); grid on; [x,y]ginput(8); %在下方命令窗…

【斗医】【18】Web应用开发20天
原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 、作者信息和本声明。否则将追究法律责任。http://qingkechina.blog.51cto.com/5552198/1544928 本文通过获取首页内容来讲解Web页面拖拽获取当前页数据,功能类似在google查看图…

数据库和缓存一致性的问题
经常看到有人问怎么解决数据库和缓存一致性的问题,这个问题我觉得是不要去解决。 如果你不信你先看我列的几种情况 假设 数据库一开始和缓存都是1元。 用户更新数据库的同时双写缓存。 1.双写不删 写库充值10元>>>返回成功 ----- 时间间隔 <<<…
【MATLAB】数据分析之求函数的极限(limit)
在MATLAB中采用limit函数求某个具体函数的极限,其调用格式如下: limit(expr,x,a):当xa时,对函数expr求极限,返回值为函数极限。limit(expr):默认当x0时,对函数expr求极限,返回值为函…
Spring Boot集成Swagger导入YApi@无界编程
接口APi开发现状 现在开发接口都要在类似YApi上写文档,这样方便不同的团队之间协作,同步更新接口,提高效率。 但是如果接口很多,你一个个手工在YApi去录入无疑效率很低。 如果是使用Spring Boot集成Swagger可以直接导入YApi非常…
【MATLAB】数据分析之函数数值积分
一、数值积分问题的数学表达 称为积分节点,称为求积系数。右端公式称为左端定积分的某个数值积分。MATLAB支持三重以下的积分运算。分别为: 在计算积分时,要求积分区间是确定的。 二、一元函数的数值积分 1、quad函数:采用遍历的…

c++对象切片
什么事对象切片:c在将一个派生类转换为基类的过程中,派生类的一部分将被基类接收不到,只能留下基类大小的对象。传值调用的切片:#include<iostream> using namespace std; class Base { public: virtual void func1() { cou…

javascript数据结构与算法-队列
定义 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为…

Oracle学习笔记十三 触发器
2019独角兽企业重金招聘Python工程师标准>>> 简介 触发器是当特定事件出现时自动执行的存储过程,特定事件可以是执行更新的DML语句和DDL语句,触发器不能被显式调用。 触发器的功能: 1.自动生成数据 2.自定义复杂的安全权限 3.提供…
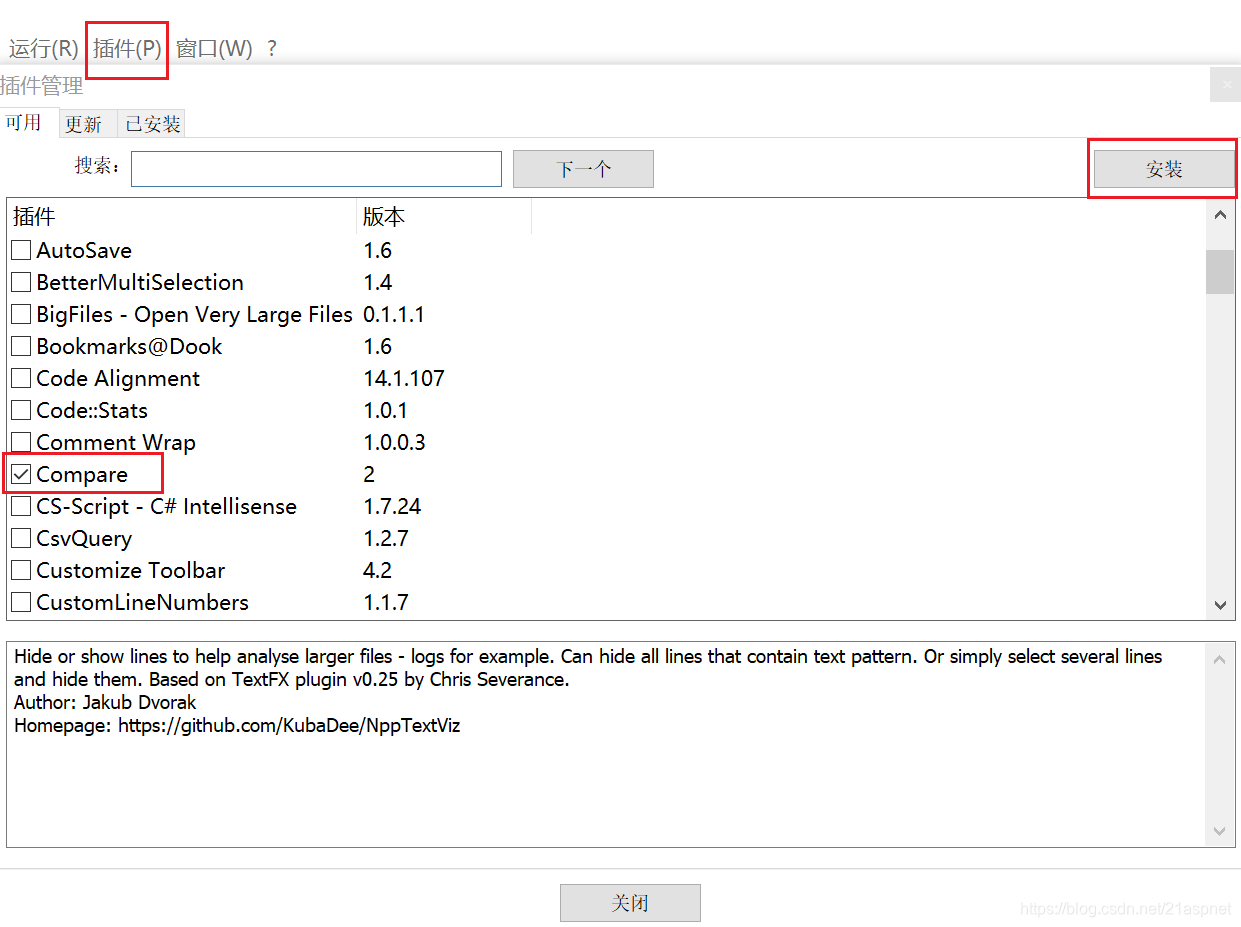
使用Notepad++比较文件的差异
有时候需要比较两个文件的差异部分,如果不在git里可以使用Notepad的插件。 在Notepad中安装Compare插件 打开NotePad,点击工具栏上的插件--Plugin Manager--Show Plugin Manager,选中Compare 然后安装。 比如下看两个线程堆栈的差异…
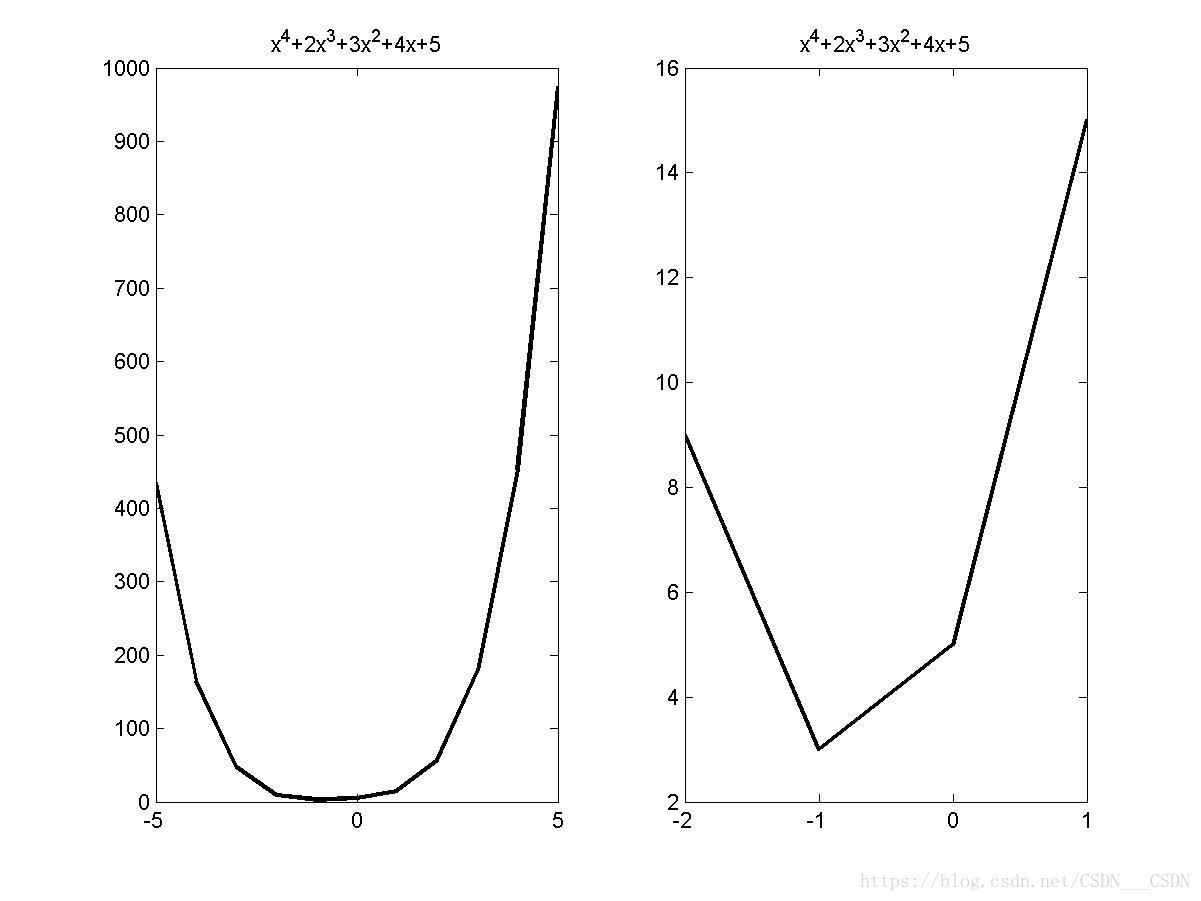
【MATLAB】将向量表示的多项式用字符串输出的通用函数示例
%创建一个名为pprintf的M文件 function s pprintf(p) %UNTITLED7 此处显示有关此函数的摘要 % 此处显示详细说明 if nargin>1error(Too much input arguments); end while(p(1)0)p1[]; end llength(p); if l0s0; elseif l1snum2str(p(1)); elseif l2s strcat(num2str(p(…

30秒或更短的时间内弄懂的有用CSS代码片段
今天无意间看到这个,真的很牛逼,记录下中文网: caibaojian.com/30-seconds-…转载于:https://juejin.im/post/5bf278a85188255e9b61a226
【MATLAB】数据分析之多项式及其函数
1、多项式的表达式和创建 MATLAB中使用一维向量来表示多项式。将多项式按照降幂次序存放在向量中。 多项式就可以用向量 [2 3 5 0 1]来表示。 2、多项式求根 >> p[1 2 1]p 1 2 1>> r roots(p)r -1-13、由根创建多项式 >> r [2;3]r 23>>…
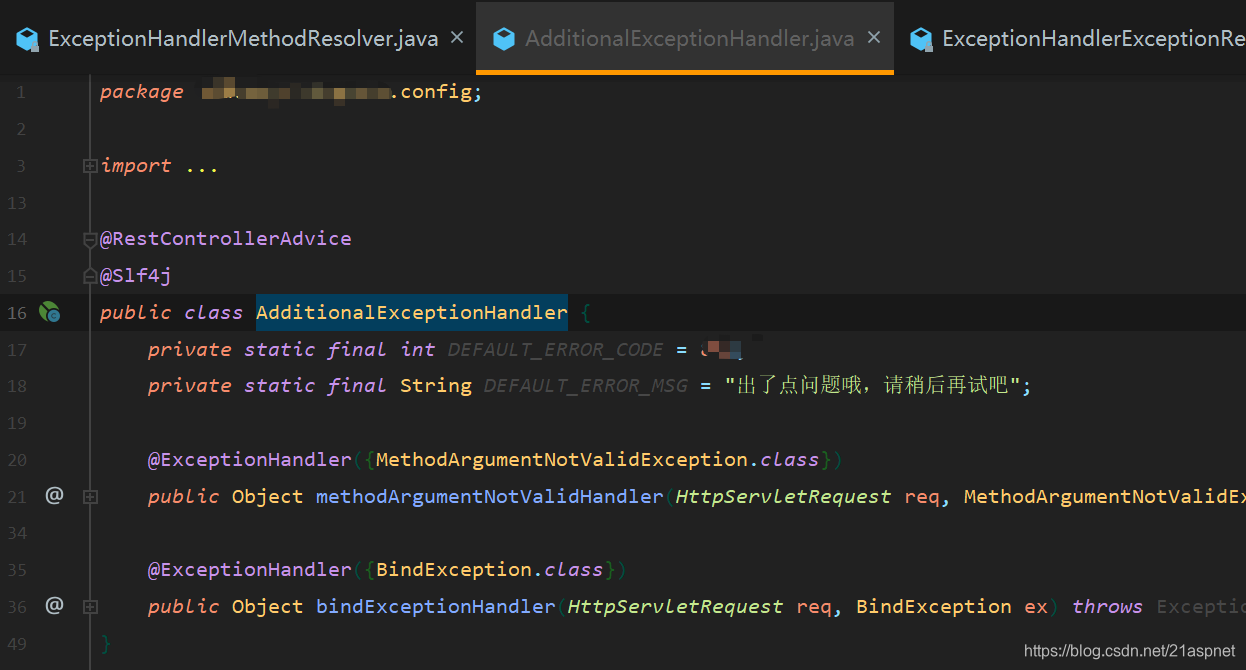
SpringBoot自定义异常源码分析
SpringBoot自定义异常源码分析 在类上加ControllerAdvice注解,在方法上加ExceptionHandler注解,就可以在方法里处理相应的异常。 1.自定义异常处理类AdditionalExceptionHandler 挂RestControllerAdvice注解: ------------------ 2.自定义…

Android 应用性能优化-StrictMode(严格模式)
为什么80%的码农都做不了架构师?>>> UI线程如果被阻塞5秒的话,那么应用程序此时就会弹出ANR的对话框,ANR对应用程序来说是一个很严重的问题。 如何防止应用程序出现ANR,怎么分析查看导致ANR问题的原因? 我…
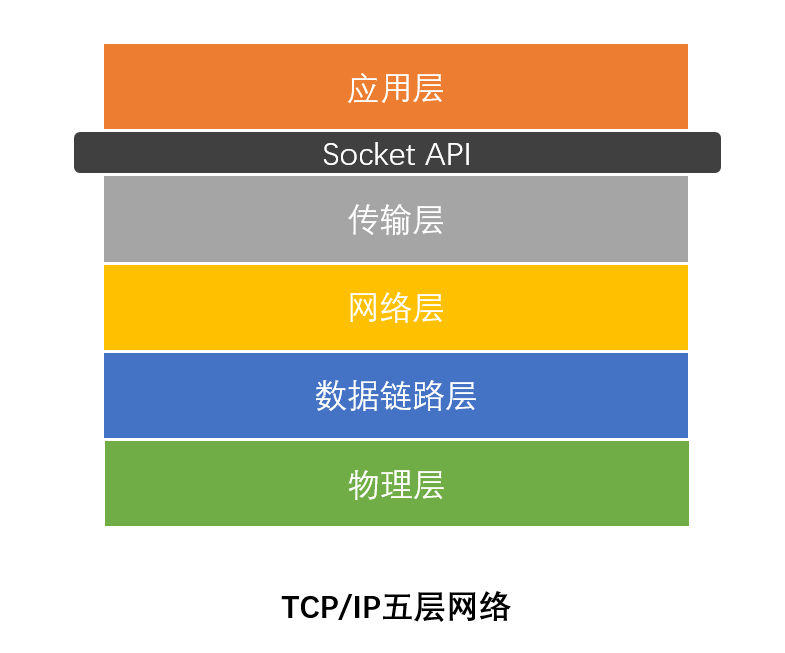
跨进程通信,到底用长连接还是短连接
一个完整的软件系统大多数情况下是由多个进程共同协作进行的,哪怕它们在同一台服务器上。所以,进程之间如何进行高效的通信至关重要。 单个应用程序单个数据库这套基础开发套餐我相信每个人都经历过,甚至在初期它们还有可能部署在同一台服务器…
Java的List和Json转换以及StringRedisTemplate往redis存泛型对象
List转Json List<User> user new ArrayList(); String str JSON.toJSONString(user); Json 转List方法一 List<User> user JSON.parseArray(json,User.class); 如果是泛型方法需要使用TypeReference Json 转List 方法二 String json "[{}]"; Li…

【MATLAB】符号数学计算(一):符号对象的创建
一、符号对象的创建命令 1、函数命令sym( ) variablesym(A,flag)Ssym(A,flag) 如果A是(不带单引号)是一个数字、数值矩阵或者数值表达式,则输出结果是将数值对象转换成的符号对象。 如果A(带单引号)是一个字符串,输出结果则是将字符串转换成的符号对象…
分布式session一致性问题
传统的网站结构(并发量不大,没有session的不一致的问题。传统的网站结构图: **结论:**从图中可以看出在传统的网站结构中,所有的客户端都连接一个服务器,每个客户端发送过来的请求都被该服务器处理&#…
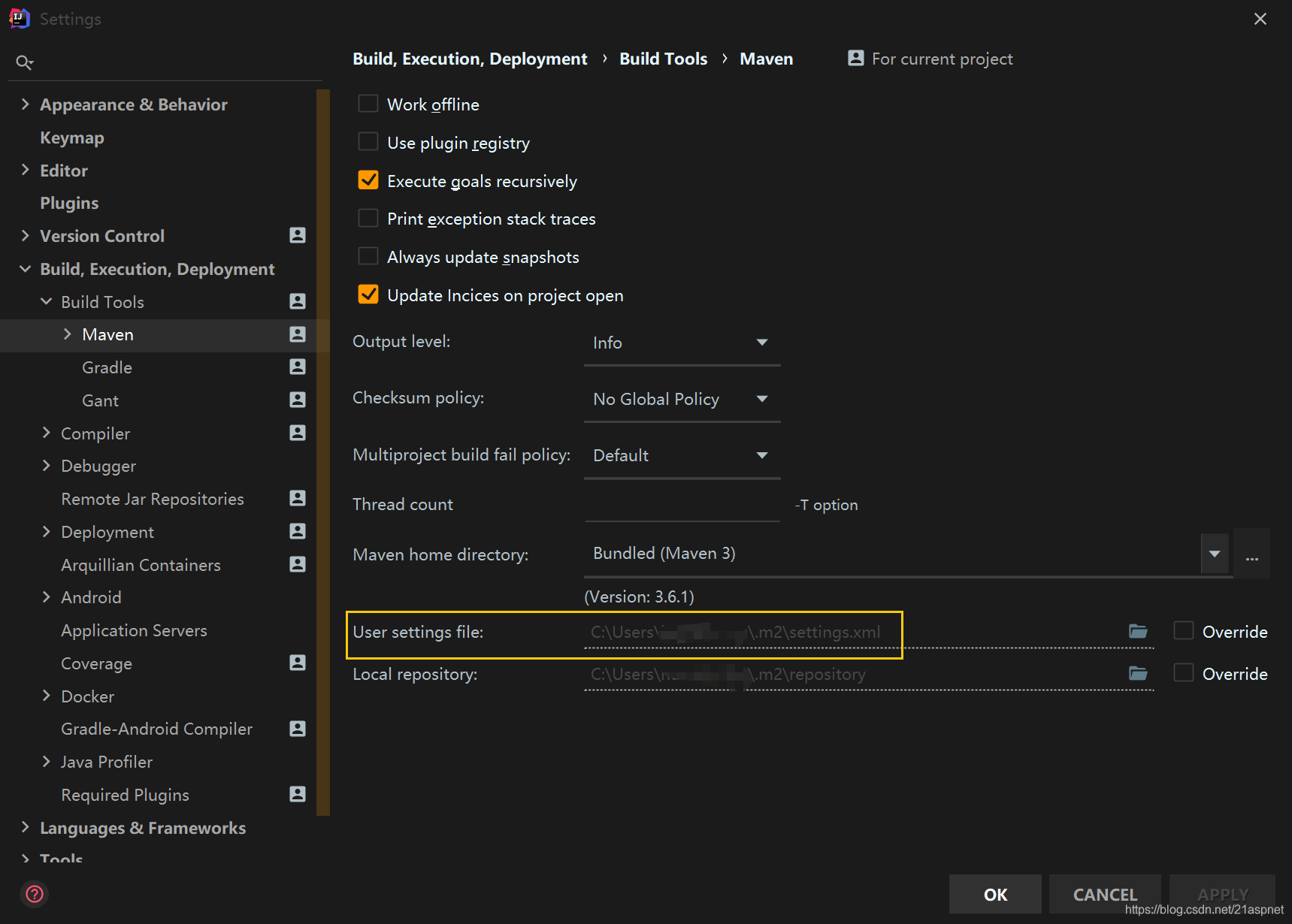
切换阿里云maven源解决maven中央仓库下载太慢卡顿的问题
maven默认官方的中央仓库有时候很慢下载jar甚至会卡住,那么你可以切换到阿里云的maven源 在本地的maven文件夹新建settings.xml <?xml version"1.0" encoding"UTF-8"?> <settings xmlns"http://maven.apache.org/SETTINGS/1.…

【MATLAB】符号数学计算(二):符号运算中的运算符和函数
一般的这里就不再列举 1、算术运算符号 运算符号“ ”、“ . ”分别实现矩阵的共轭转置和非共轭转置。 >> syms a b c d; >> Asym([a,b;c,d])A [ a, b] [ c, d]>> R1AR1 [ conj(a), conj(c)] [ conj(b), conj(d)]>> R2A.R2 [ a, c] [ b, d] 2、关…

2015级C++第14周实践项目 模板
【项目1-排序函数模板】 已知 void Sort(int a[],int size); void Sort(double a[],int size); 是一个函数模板的两个实例,其功能是将数组a中的前size个元素按从小到大顺序排列。试设计这个函数模板。 【项目2-两个成员的类模板】 设有如下的类声明&#…

11月18日珠三角城市人口迁徙可视化(和弦图)
2019独角兽企业重金招聘Python工程师标准>>> 一、导入数据,初始图 > library(circlize) > data<-read.table("C:/Users/cuiy/Desktop/PersonalData/qianxi.csv",sep",",headerT) > head(data)from to value 1 中山 珠…

【MATLAB】符号数学计算(三):符号的精度计算
符号计算的一个非常显著的特点是,由于计算中不会出现舍入误差,从而可以得到任意精度的数值解。 (要计算精确,就要牺牲计算时间和储存空间) 符号工具箱中有三种不同类型的算术运算: 数值类型:…

SQLite第三方框架FMDB的使用,以及使用FMDatabaseQueue保证线程安全
2019独角兽企业重金招聘Python工程师标准>>> (1)下载地址:https://github.com/ccgus/fmdb (2)注意点 ——语句可以带分号“;”,也可以省略分号。 ——同样需要添加“libsqlite3.dyli…

Linus采访对Linux对git和对代码品味的理解
【Linus对办公环境的要求】 Linus大师说他11岁就开始编程,他说他是一个喜欢安静和不合群的人。 图中是他和他的弟弟,看来少儿编程还是很重要的,大师21岁写出linux0.0.1最初的内核。 图中是他的家,也是Linux的总部,非常简单的办公环境,只有显示器,大师喜欢安静,所以不想…

04 集成学习 - Boosting - AdaBoost算法构建
03 集成学习 - Boosting - AdaBoost算法原理 十、AdaBoost算法构建 上一章最后说明了每个基模型的权值α是如何求得的,于是我就可以对模型进行更新操作了。 构建过程一 1、假设数据集: T{(X1,Y1),(X2,Y2),...(Xn,Yn)} 2、初始化训练数据权重分布…
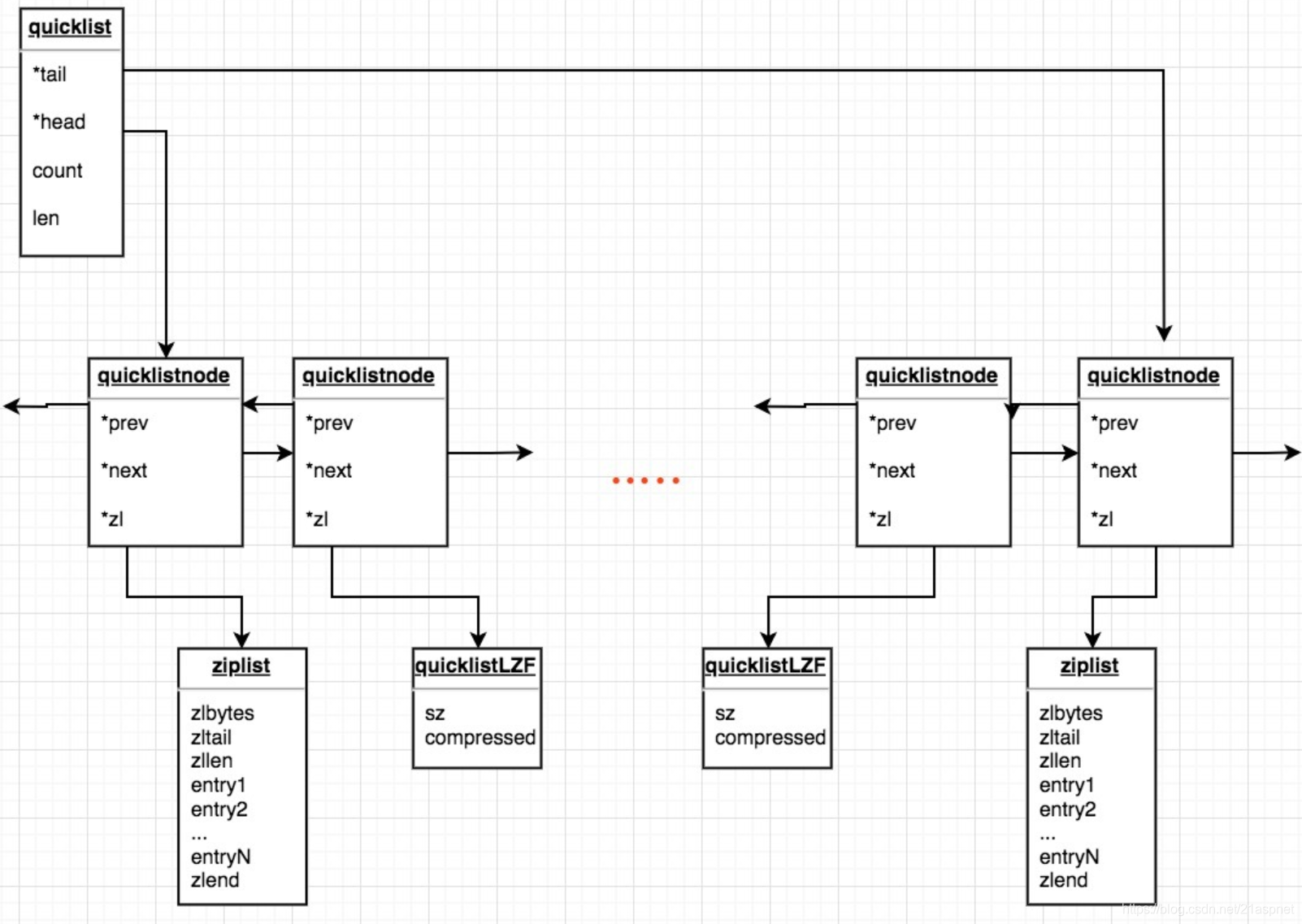
Redis源码分析 List实现
在版本3.2之前,Redis中的列表是 ziplist 和 linkedlist 实现的,在3.2之后,由quicklist实现。 双向链表linkedlist在表的两端进行push和pop操作非常方便,但是地址不连续,而且需要保持额外的指针。 ziplist是连续内存&am…

Linux cut命令
用途 文本文件按列提取。 特点 过于简单,只能处理固定格式的分隔符,分隔符不能使用正则表达式。 用法 命令基本格式 -b、-c、-f分别表示字节、字符、字段(即byte、character、field);list表示-b、-c、-f操作范围&#…

【MATLAB】符号数学计算(四):符号表达式操作
一、符号表达式合并 Rcollect(S):将表达式S中相同次幂的项合并。S可以是一个表达式,也可以是一个符号矩阵。Rcollect(S,v):将表达式中S中v的相同次幂进行合并。如果v没有指定,则默认将含有x的相同次幂的项进行合并。 >> sy…
