迈斯！啊呸~数学

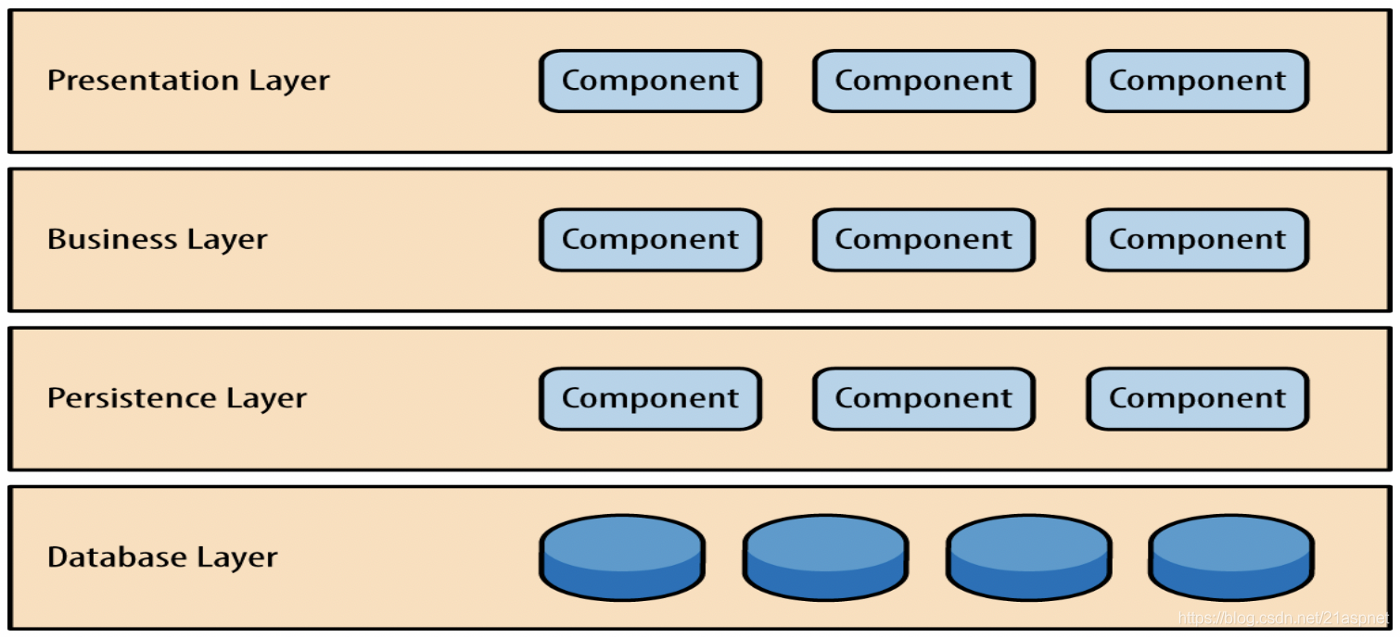
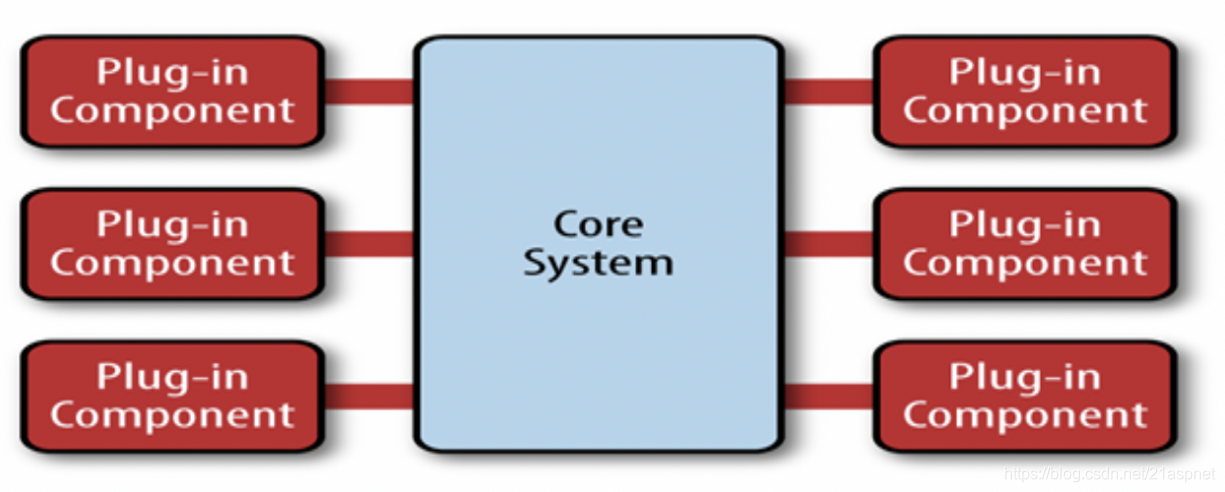
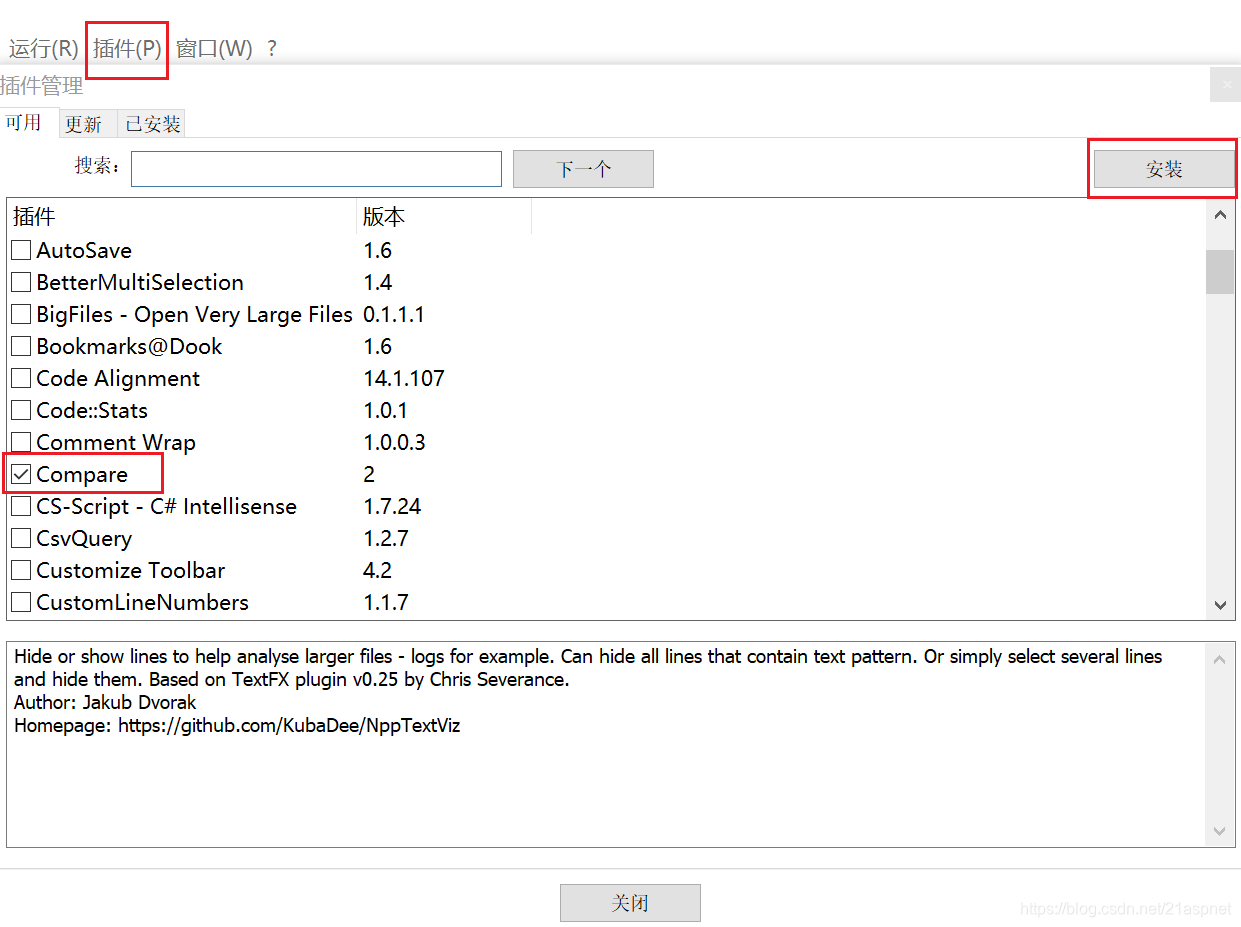
1.数论

快速幂

int po(int x,int y)
{int ans=1;while(y){if(y%2==1)ans=1ll*ans*x%p;x=1ll*x*x%p;y/=2;}return ans;
}

乘法逆元（保证模域p与求逆元的数互质）

po(a,p-2);//a为需要求逆元的数

扩展欧几里得（exgcd）

#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
ll exgcd(ll a,ll b,ll &x,ll &y)
{if(b==0){x=1;y=0; return a;}exgcd(b,a%b,x,y);ll tx=x;x=y;y=tx-a/b*y;
}
int main()
{ll a,b;scanf("%lld%lld",&a,&b);ll x,y;exgcd(a,b,x,y);while(x<0){x+=b;}x%=b;printf("%lld\n",x);return 0;
}

acos(-1.0)是圆周率，或者是cmath库里的M_PI也是圆周率，只有15位有效数字。