软件体系架构模式之二分层体系结构
分层体系结构模式是n层模式,其中组件被组织在水平层中。这是设计大多数软件的传统方法,并且具有独立性。这意味着所有组件都是互连的,但彼此之间不依赖。
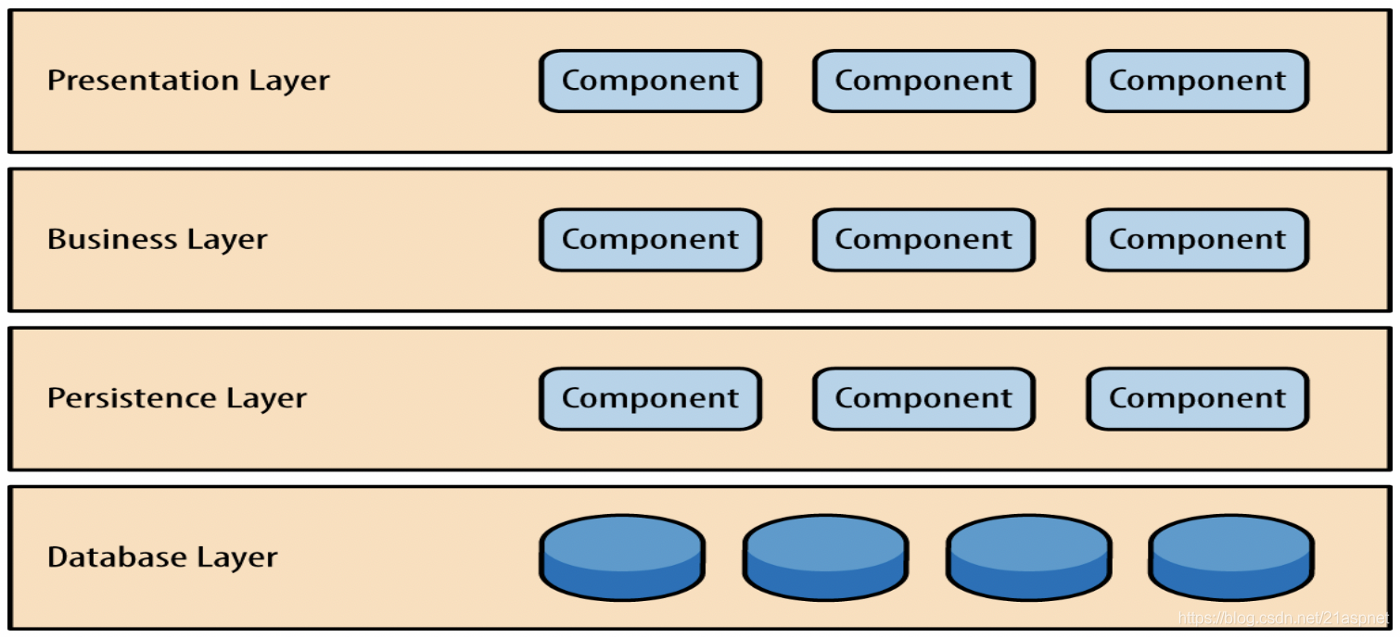
图1:分层架构
在此体系结构中有四层,其中每一层在模块和其中的组件之间都有联系。从上到下分别是:
表示层:它包含与表示层相关的所有类别。
业务层:包含业务逻辑。
持久层:用于处理对象关系映射之类的功能
数据库层:这是所有数据的存储位置。
在这种情况下,层是关闭的,这意味着请求必须从上到下遍历所有层。这样做有两个原因,一个是所有“相似”组件都在一起,另一个是它提供了隔离层。
详细地说,将“相似”的组件放在一起意味着与某个层相关的所有内容都停留在该单个层中。这样一来,就可以在组件的类型之间进行清晰的分隔,并且还可以将类似的编程代码集中在一个位置。通过隔离各层,它们变得彼此独立。因此,例如,如果我们要将数据库从Oracle服务器更改为SQL服务器,这将对数据库层产生很大的影响,但不会影响其他任何层。同样,假设您有一个自定义的书面业务层,并想为业务规则引擎进行更改。如果我们拥有定义良好的分层体系结构,则更改不会影响其他层。
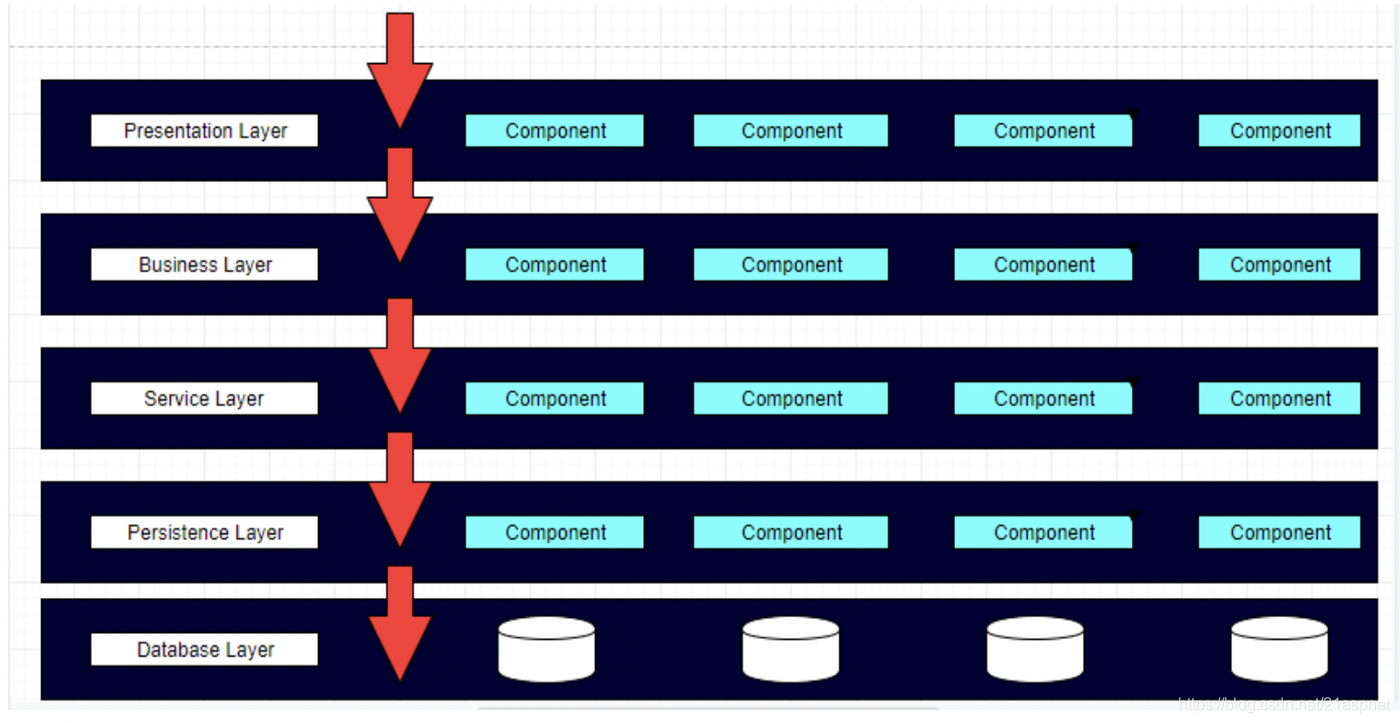
图2:分层架构中的数据传播
可以对分层体系结构模式进行修改,以在提到的层之外增加其他层。这称为混合分层体系结构。例如,在业务层和持久层之间可以有一个服务层。但是,这不是理想的方案,因为现在业务层必须经过服务层才能到达持久层。通过服务层,此请求不会获得任何价值。我们将其称为架构漏洞反模式。请求通过层,而在每个层中执行的逻辑很少或没有逻辑。
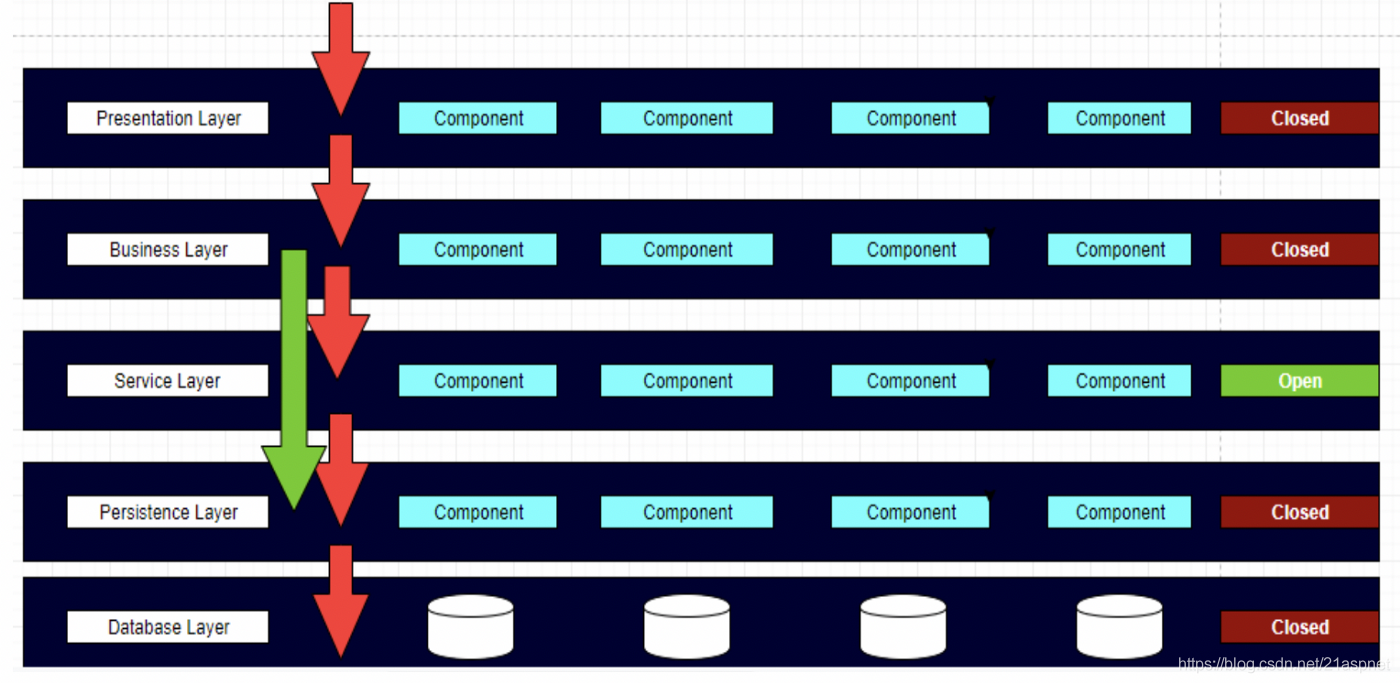
图3:分层架构模式中的开放层
解决此问题的唯一方法是将可选层设置为开放层。这意味着,如果可选层将任何值添加到正在发送的请求中,那么请求将通过它。如果不是,那么它将简单地绕过该层,然后转到相关层。从上图中可以看出,请求绕过了服务层,并从业务层移到了持久层。
但是请注意,通过使用开放层,可以消除使用隔离层的好处。如果要交换持久层,则必须考虑开放服务层以及业务层。这两个层现在都耦合到持久层。因此,尽管很容易向系统中添加开放层,但不应允许它发生。我们必须设法解决问题而不损害体系结构。
结论
分层架构是软件架构模式的最简单形式。如果您要设计一个基本的应用程序,其中用户数量很少(<100–200),并且您确定上线后不会有太多的需求变更,那么这是最好的软件架构模式。与其他模式相比,此体系结构模式的实现成本非常低。
以下是分层架构模式的利弊分析。
优点
由于组件属于特定层,因此易于测试。因此,它们可以单独进行测试。
它很容易实现,因为自然而然,大多数应用程序都是分层工作的。
缺点
尽管可以对特定的层进行更改,但这并不容易,因为应用程序是单个单元。而且,层之间的耦合趋于使其变硬。这也使得难以扩展。
必须将其部署为单个单元,因此更改为特定层意味着必须重新部署整个系统。
它越大,请求通过多个层所需的资源就越多,因此将导致性能问题。
原文:https://medium.com/@priyalwalpita
相关文章:

linux下mysql的root密码忘记解决方法
1.首先确认服务器出于安全的状态,最安全的状态是到服务器的Console上面操作,并且拔掉网线,或者可以使用--skip-networking限制只能从本地连接2.修改MySQL的登录设置: # vim /etc/my.cnf在[mysqld]的段中加上…

【Python】turtle库的小应用
心血来潮,哈哈哈,画的不好,请多见谅 大家如果想要尝试turtle库,可以借鉴: https://www.cnblogs.com/nowgood/p/turtle.html 导入库,我的pycharm里可以直接使用,哈哈哈,不行就pip…

[转]MySQL修改时区的方法小结
本文转自:https://www.cnblogs.com/mracale/p/6064447.html 这篇文章主要介绍了MySQL修改时区的方法,总结分析了三种常见的MySQL时区修改技巧,包括命令行模式、配置文件方式及代码方式,需要的朋友可以参考下 方法一:通过mysql命令行模式下动态修改 1.1 查…

swift轮播图代码
import UIKit private let CycleCellID "CycleCellID" class BannerCycleView: UIView { var layout : UICollectionViewFlowLayout! var collectionView :UICollectionView! var pageContol : UIPageControl? var cycleTimer : Timer? let timeInterval : TimeI…
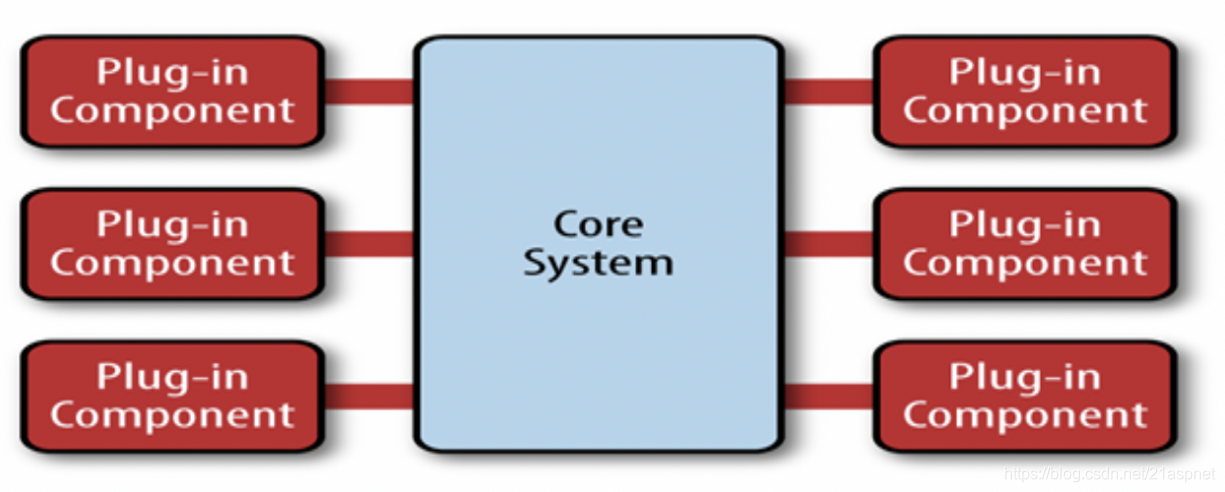
软件体系架构模式之三微内核体系架构
当您的软件系统或产品包含许多与外部实体的集成点时,微内核体系结构模式将非常有用。最重要的是,您将无法准确判断出将来将哪些实体集成到您的系统中。可以将微内核架构模式识别为基于插件的模式。。也称为插件架构模式,它由两个主要组件组成…

【MATLAB】交互式绘图(ginput,gtext,zoom)
1、ginput指令: [x,y]ginput(n) %(其功能是用鼠标从二维图形中获取n个点的数据坐标) x-8*pi:pi/100:8*pi; y1sin(x); y24*sin(x/4); plot(x,y1,r-,x,y2,k-); legend(sin(x),4sin(x/4)); grid on; [x,y]ginput(8); %在下方命令窗…

【斗医】【18】Web应用开发20天
原创作品,允许转载,转载时请务必以超链接形式标明文章 原始出处 、作者信息和本声明。否则将追究法律责任。http://qingkechina.blog.51cto.com/5552198/1544928 本文通过获取首页内容来讲解Web页面拖拽获取当前页数据,功能类似在google查看图…

数据库和缓存一致性的问题
经常看到有人问怎么解决数据库和缓存一致性的问题,这个问题我觉得是不要去解决。 如果你不信你先看我列的几种情况 假设 数据库一开始和缓存都是1元。 用户更新数据库的同时双写缓存。 1.双写不删 写库充值10元>>>返回成功 ----- 时间间隔 <<<…
【MATLAB】数据分析之求函数的极限(limit)
在MATLAB中采用limit函数求某个具体函数的极限,其调用格式如下: limit(expr,x,a):当xa时,对函数expr求极限,返回值为函数极限。limit(expr):默认当x0时,对函数expr求极限,返回值为函…
Spring Boot集成Swagger导入YApi@无界编程
接口APi开发现状 现在开发接口都要在类似YApi上写文档,这样方便不同的团队之间协作,同步更新接口,提高效率。 但是如果接口很多,你一个个手工在YApi去录入无疑效率很低。 如果是使用Spring Boot集成Swagger可以直接导入YApi非常…
【MATLAB】数据分析之函数数值积分
一、数值积分问题的数学表达 称为积分节点,称为求积系数。右端公式称为左端定积分的某个数值积分。MATLAB支持三重以下的积分运算。分别为: 在计算积分时,要求积分区间是确定的。 二、一元函数的数值积分 1、quad函数:采用遍历的…

c++对象切片
什么事对象切片:c在将一个派生类转换为基类的过程中,派生类的一部分将被基类接收不到,只能留下基类大小的对象。传值调用的切片:#include<iostream> using namespace std; class Base { public: virtual void func1() { cou…

javascript数据结构与算法-队列
定义 队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为…

Oracle学习笔记十三 触发器
2019独角兽企业重金招聘Python工程师标准>>> 简介 触发器是当特定事件出现时自动执行的存储过程,特定事件可以是执行更新的DML语句和DDL语句,触发器不能被显式调用。 触发器的功能: 1.自动生成数据 2.自定义复杂的安全权限 3.提供…
使用Notepad++比较文件的差异
有时候需要比较两个文件的差异部分,如果不在git里可以使用Notepad的插件。 在Notepad中安装Compare插件 打开NotePad,点击工具栏上的插件--Plugin Manager--Show Plugin Manager,选中Compare 然后安装。 比如下看两个线程堆栈的差异…
【MATLAB】将向量表示的多项式用字符串输出的通用函数示例
%创建一个名为pprintf的M文件 function s pprintf(p) %UNTITLED7 此处显示有关此函数的摘要 % 此处显示详细说明 if nargin>1error(Too much input arguments); end while(p(1)0)p1[]; end llength(p); if l0s0; elseif l1snum2str(p(1)); elseif l2s strcat(num2str(p(…

30秒或更短的时间内弄懂的有用CSS代码片段
今天无意间看到这个,真的很牛逼,记录下中文网: caibaojian.com/30-seconds-…转载于:https://juejin.im/post/5bf278a85188255e9b61a226
【MATLAB】数据分析之多项式及其函数
1、多项式的表达式和创建 MATLAB中使用一维向量来表示多项式。将多项式按照降幂次序存放在向量中。 多项式就可以用向量 [2 3 5 0 1]来表示。 2、多项式求根 >> p[1 2 1]p 1 2 1>> r roots(p)r -1-13、由根创建多项式 >> r [2;3]r 23>>…
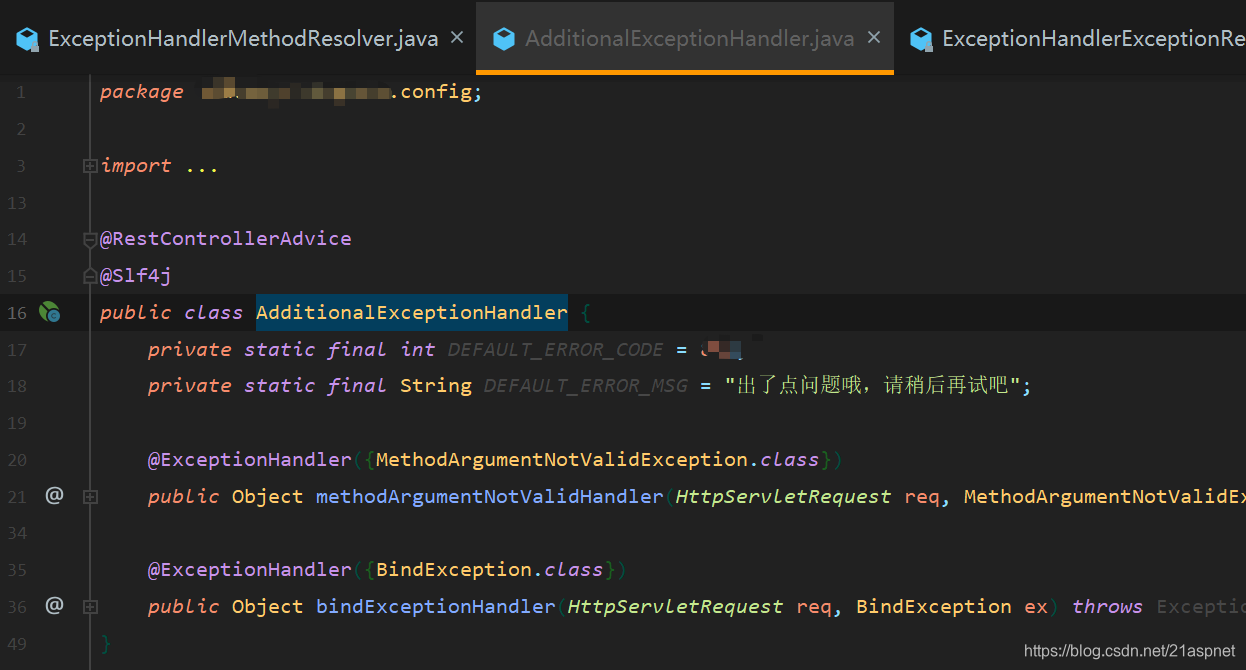
SpringBoot自定义异常源码分析
SpringBoot自定义异常源码分析 在类上加ControllerAdvice注解,在方法上加ExceptionHandler注解,就可以在方法里处理相应的异常。 1.自定义异常处理类AdditionalExceptionHandler 挂RestControllerAdvice注解: ------------------ 2.自定义…

Android 应用性能优化-StrictMode(严格模式)
为什么80%的码农都做不了架构师?>>> UI线程如果被阻塞5秒的话,那么应用程序此时就会弹出ANR的对话框,ANR对应用程序来说是一个很严重的问题。 如何防止应用程序出现ANR,怎么分析查看导致ANR问题的原因? 我…
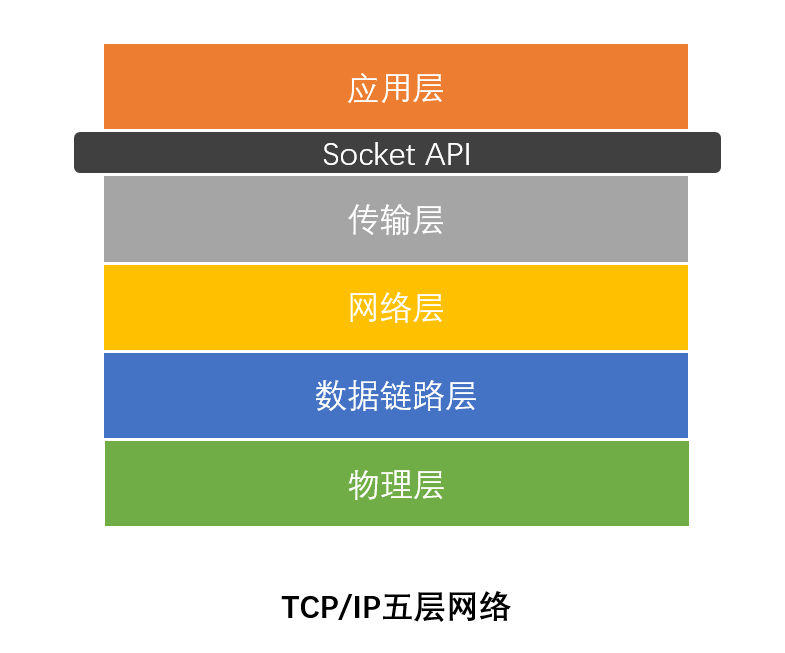
跨进程通信,到底用长连接还是短连接
一个完整的软件系统大多数情况下是由多个进程共同协作进行的,哪怕它们在同一台服务器上。所以,进程之间如何进行高效的通信至关重要。 单个应用程序单个数据库这套基础开发套餐我相信每个人都经历过,甚至在初期它们还有可能部署在同一台服务器…
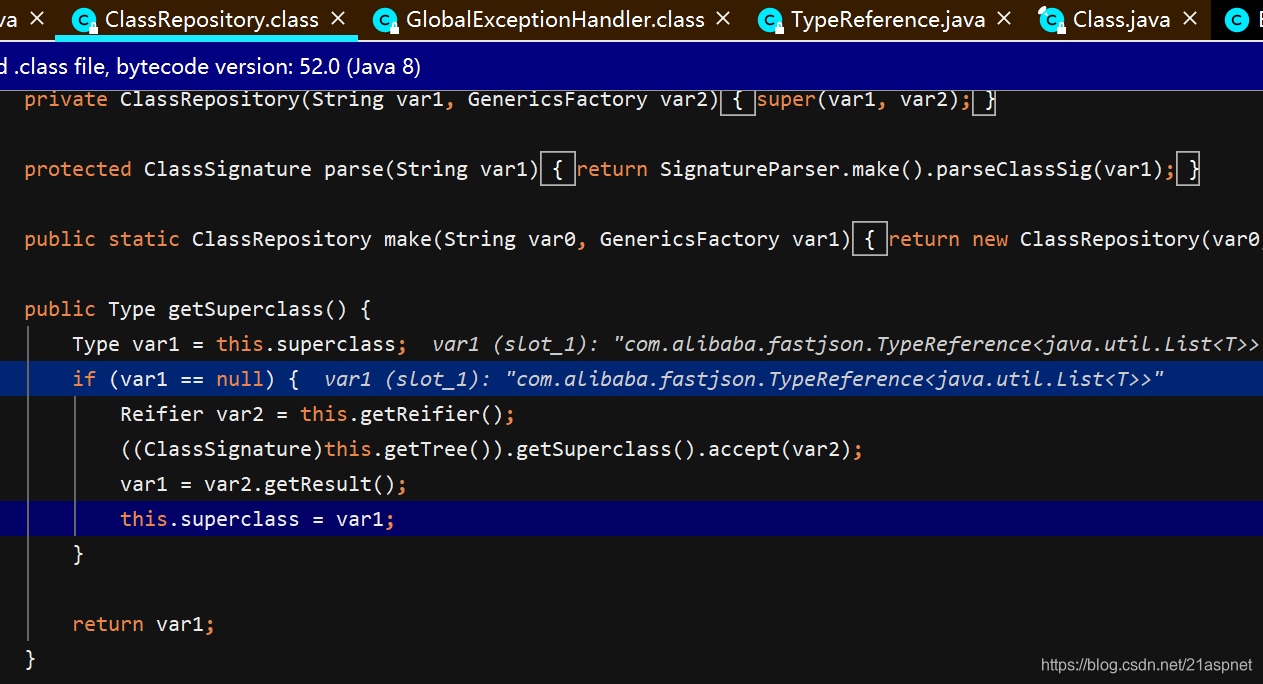
Java的List和Json转换以及StringRedisTemplate往redis存泛型对象
List转Json List<User> user new ArrayList(); String str JSON.toJSONString(user); Json 转List方法一 List<User> user JSON.parseArray(json,User.class); 如果是泛型方法需要使用TypeReference Json 转List 方法二 String json "[{}]"; Li…

【MATLAB】符号数学计算(一):符号对象的创建
一、符号对象的创建命令 1、函数命令sym( ) variablesym(A,flag)Ssym(A,flag) 如果A是(不带单引号)是一个数字、数值矩阵或者数值表达式,则输出结果是将数值对象转换成的符号对象。 如果A(带单引号)是一个字符串,输出结果则是将字符串转换成的符号对象…
分布式session一致性问题
传统的网站结构(并发量不大,没有session的不一致的问题。传统的网站结构图: **结论:**从图中可以看出在传统的网站结构中,所有的客户端都连接一个服务器,每个客户端发送过来的请求都被该服务器处理&#…
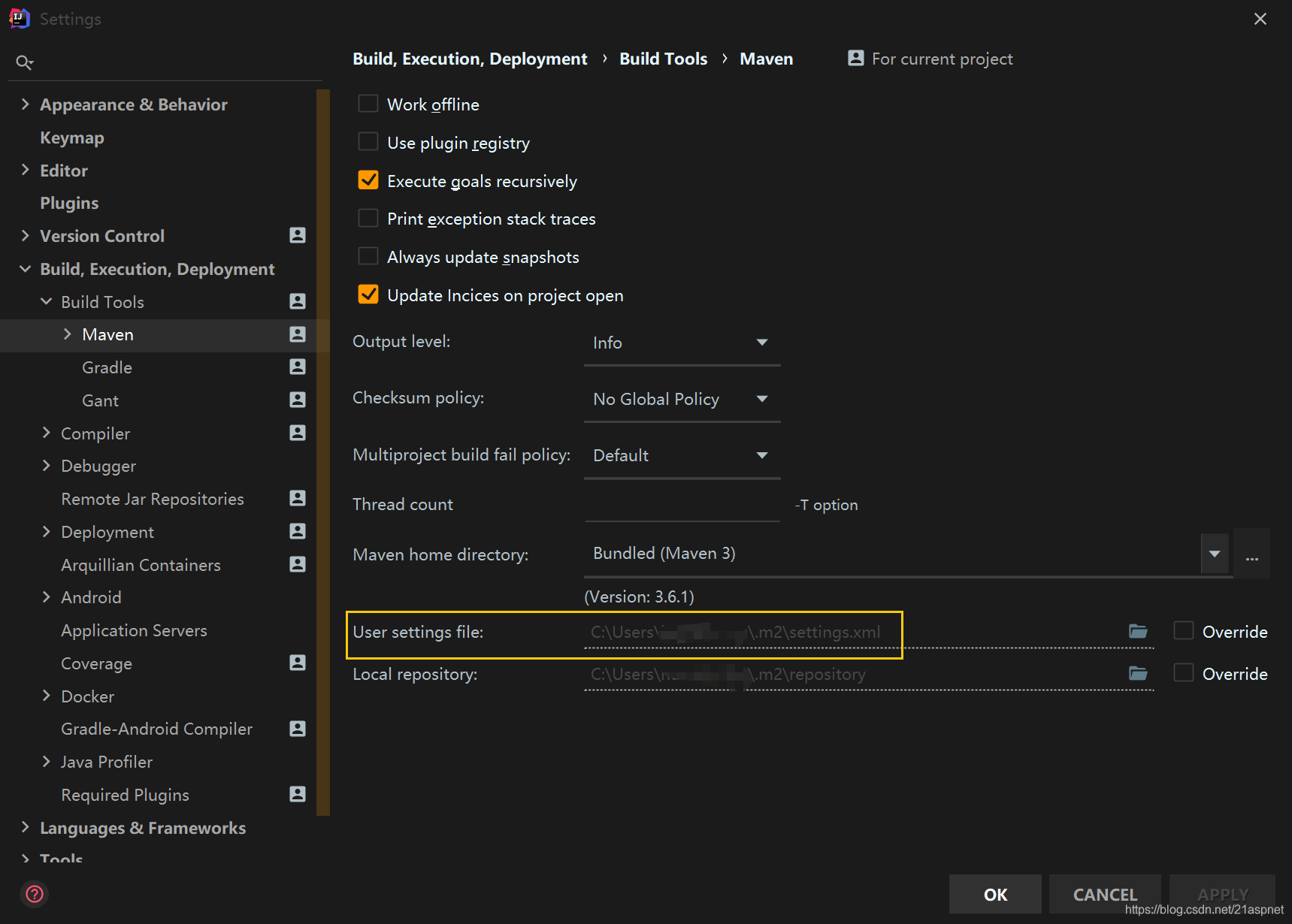
切换阿里云maven源解决maven中央仓库下载太慢卡顿的问题
maven默认官方的中央仓库有时候很慢下载jar甚至会卡住,那么你可以切换到阿里云的maven源 在本地的maven文件夹新建settings.xml <?xml version"1.0" encoding"UTF-8"?> <settings xmlns"http://maven.apache.org/SETTINGS/1.…

【MATLAB】符号数学计算(二):符号运算中的运算符和函数
一般的这里就不再列举 1、算术运算符号 运算符号“ ”、“ . ”分别实现矩阵的共轭转置和非共轭转置。 >> syms a b c d; >> Asym([a,b;c,d])A [ a, b] [ c, d]>> R1AR1 [ conj(a), conj(c)] [ conj(b), conj(d)]>> R2A.R2 [ a, c] [ b, d] 2、关…

2015级C++第14周实践项目 模板
【项目1-排序函数模板】 已知 void Sort(int a[],int size); void Sort(double a[],int size); 是一个函数模板的两个实例,其功能是将数组a中的前size个元素按从小到大顺序排列。试设计这个函数模板。 【项目2-两个成员的类模板】 设有如下的类声明&#…

11月18日珠三角城市人口迁徙可视化(和弦图)
2019独角兽企业重金招聘Python工程师标准>>> 一、导入数据,初始图 > library(circlize) > data<-read.table("C:/Users/cuiy/Desktop/PersonalData/qianxi.csv",sep",",headerT) > head(data)from to value 1 中山 珠…

【MATLAB】符号数学计算(三):符号的精度计算
符号计算的一个非常显著的特点是,由于计算中不会出现舍入误差,从而可以得到任意精度的数值解。 (要计算精确,就要牺牲计算时间和储存空间) 符号工具箱中有三种不同类型的算术运算: 数值类型:…

SQLite第三方框架FMDB的使用,以及使用FMDatabaseQueue保证线程安全
2019独角兽企业重金招聘Python工程师标准>>> (1)下载地址:https://github.com/ccgus/fmdb (2)注意点 ——语句可以带分号“;”,也可以省略分号。 ——同样需要添加“libsqlite3.dyli…
