字符串的模式匹配 (朴素模式匹配算法 ,KMP算法)
字符串的模式匹配
寻找字符串p在字符串t中首次出现的起始位置
字符串的顺序存储
typedef struct
{char str[MAXSIZE];int length;
}seqstring;朴素的模式匹配算法
基本思想:用p中的每一个字符去与t中的字符一一比较。
模式p 正文 t
如果匹配成功,则返回p在t中首次出现的起始位置
如果匹配不成功则返回-1
最坏情况比较次数可达:(n-m+1)*m次
int index(seqstring p,seqstring t)
{int i,j,flag;i=0;flag=0;while((i<=t.length-p.length) && (!flag)){j=0;flag=1;while(j<p.length && flag){if(p.str[j]==t.str[i+j]){j++;}else{flag=0;}}++i;}if(flag){return (i-1);}else{ return -1;}
}或者另一种朴素模式匹配算法
int index(seqstring t,seqstring p)
{//t是文本串,p是模式串int i=0,j=0;while(i<t.length && j<p.length){if(p.str[j]==t.str[i]){i++;j++;}else{i=i-j+1;//需要琢磨j=0;}}if(j==p.length){return (i-j);}else{return -1;}
}在学习KMP算法之前:
真前缀:除了自身以外,一个字符串的全部头部组合。
真后缀:除了自身以外,一个字符串的全部尾部组合。
(注意区分 前缀 和 真前缀)
KMP算法的流程:
假设现在文本串S匹配到i位置,模式串P匹配到j位置
如果j==-1 或者 当前字符匹配成功,则i++,j++,继续匹配下一个字符
如果匹配失败,那么模式串向右移动的位数:失配字符所在位置-失配字符对应的next值。
这时:j=6,next[j]=2,所以向右移动 j-next[j]=6-2=4个位置。
或者基于《最大长度表》:以匹配字符数-失配字符的上一位字符所对应的最大长度值
这时:以匹配字符为6,失配字符的上一位字符所对应的最大长度值=2,所以向右移动 6-2=4个位置。
int KMP_search(seqstring s,seqstring p,int next[])//文本串S,模式串P
{int i=0,j=0;while(i<s.length && j<p.length){if(j==-1 || s.str[i]==p.str[j]){//如果j=-1或者当前字符匹配成功,即s[i]==p[j]i++;j++;}else{//当匹配失败时,模式串向右移动的位数为:失配字符所在位置-失配字符对应的next值j=next[j];}}if(j==p.length){return (i-j);}else{return -1;}
}在KMP算法中有一个next数组相当关键
所以首要的是求出next数组的各个值
next数组的求解:
求解基于“真前缀”和“真后缀”,next[i]最长相同的真前后缀的长度。
根据《最大长度表》求解next[ ]数组
例:对于字符串ABCDABD
《最大长度表》
| 字符 | A | B | C | D | A | B | D |
| 最大前后缀公共元素长度 | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
next数组相当于最大长度表向后移一位,然后初始值赋值为-1。
可以不通过这个最大长度表直接计算next数组的值,即这个字符之前的字符串有多大长度的相同的前后缀(真前后缀)。
《next[] 数组》
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | C | D | A | B | D | \0 |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
i=0时,对于模式串的首位,我们统一为next[0]=-1
i=1时,前面的字符为A,其最长相同真前后缀长度为0,next[1]=0
i=2时,前面的字符为AB,其最长相同真前后缀长度为0,next[2]=0
i=3时,前面的字符为ABC,其最长相同真前后缀长度为0,next[3]=0
i=4时,前面的字符为ABCD,其最长相同真前后缀长度为0,next[4]=0
i=5时,前面的字符为ABCDA,其最长相同真前后缀长度为1,next[5]=1
i=6时,前面的字符为ABCDAB,其最长相同真前后缀长度为2,next[6]=2
i=7时,前面的字符为ABCDABD,其最长相同真前后缀长度为0,next[7]=0
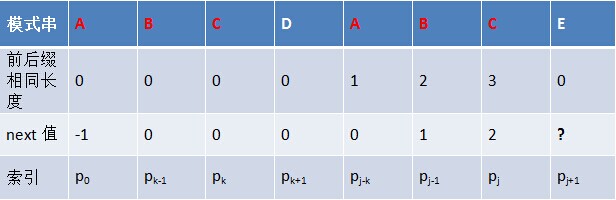
下面需要思考的是:如果知道了next[ j ],怎么得到next [ j+1]呢?
next[ j ]=k,代表 j 之前的模式子串中,有长度为 k 的相同的前缀和后缀。
有了这个next[]数组,在KMP匹配中,当模式串 j 处失配时,模式串向右移动 j-next[j] 位。
1、对于模式串来说,如果p[ j ]==p[ k ],那么next[j+1]=next[ j ]+1 = k+1(p[ k ]是前缀,p[ j ]是后缀)
这里 k=2,j=6,p[k]=p[j],所以next[ j+1 ] = next[ j ]+1 = k+1 = 2+1 = 3。
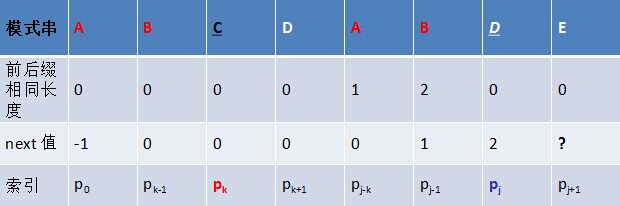
2、如果p[ j ] != p[ k ],那么就说明 “p0p1...pk-1pk” 不等于 “pj-k...pj-1pj”。
这里j=2,k=6,ABC!=ABD,那么在字符E前没有长度为k+1的相同的前后缀,需要去找一个长度更短一些的前后缀。
思路:与上面的模式串与文本串匹配类似(与KMP思路类似),当p0p1p2...pj跟主串s0s1...si匹配时,如果在模式串j处失配,则模式串需要向右移动 j-next[j] 位,相当于 j = next [ j ]。
而现在是前缀与后缀匹配,"p0p1..pk-1pk"和"pj-k...pj-1pj"匹配时,发现在pk处匹配失败,若能在前缀"p0...pk-1pk"中不断递归前缀索引k=next[k],找到一个字符pk’==pj,且满足" p0pk'-1pk' "==" pj-k'pj-1pj ",则最大相同的前后缀长度为k'+1,从而next[j+1]=k'+1=next[k']+1。否则继续递归k'=next[k'],直到next[k']=0。
void getnext(seqstring p,int next[])
{int i=0;int j=-1;next[0]=-1;while(i<p.length){if(j==-1 || p.str[j]==p.str[i]){++i;++j;next[i]=j;}else{j=next[j];}}printf("未优化:\n");for(i=0;i<p.length;i++){printf("%5d",next[i]);}printf("\n");return ;
}next数组的优化
应用上面的KMP算法,以及next[]数组的求解算法得到next数组中的各个值。
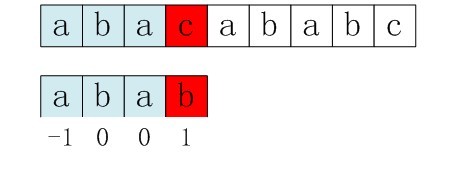
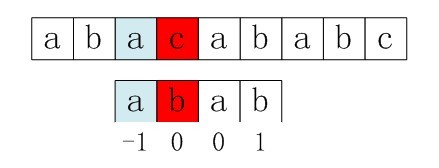
在下面这个例子中,因为 ‘c’和‘b’不匹配,所以模式串右移j-next[j]=3-1=2位。右移了两位后,又是b与c的匹配,显然也是不匹配的。那么出现这种情况的原因是:p[j]=p[ next[j] ]。因为p[j]!=p[i],如果 p[ j ]==p[ next[ j ] ] ,那么必然会导致下一次匹配的失败,所以对求解next数组的函数进行进一步的优化。
void getnext(seqstring p,int next[])
{int i=0;int j=-1;next[0]=-1;while(i<p.length){//p[j]表示前缀,p[i]表示后缀if(j==-1 || p.str[j]==p.str[i]){++i;++j;//在前j+1个字符都匹配了以后,i+1,j+1,这时如果满足下面的if条件,则next[i]就是该字符之间的相同前后缀的长度if(p.str[j]!=p.str[i]){//如果两个不相同,就直接存储前面的子串的(以匹配的)长度next[i]=j;}else{//因为出现两个字符一样的情况,所以在使用KMP算法时,为了避免出现p[j]==p[next[j]]使算法效率变低,//所以当出现时需要递归,j=next[j]=next[next[j]].next[i]=next[j];}}else{j=next[j];}}printf("优化后:\n");for(i=0;i<p.length;i++){printf("%5d",next[i]);}printf("\n");return ;
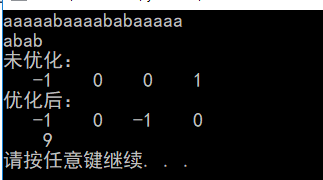
}只要出现了p[ next[ j ] ]=p[ j ]的情况,则把next[ j ]再次递归。例如在求模式串abab的next数组时,对于未优化的next数组,第二个a对应的值是0,相当于第二个a失配时,下一步匹配模式串会用p[ 0 ]处的a再次与文本串匹配,必然是失配的。所以再求第二个a的next值时,需要再次递归next[ 2 ]=next[ next[ 2 ] ]=next[0]=-1。此后,根据优化的新的next的值可知,第二个a失配时,执行" j==-1 || p.str[j]==p.str[i] ,++i,++j,继续匹配下一个字符 ",同理,对应的b的next的值为0。(可以自己手动推导,或者单步调试)。
对于优化后的next数组可以发现:如果模式串的后缀和前缀一样,例如abcdabcd,他们的前缀后缀都是abcd,其优化后的next数组是-1 0 0 0 -1 0 0 0,其前后缀的next值都是-1 0 0 0。
KMP算法的时间复杂度
回顾KMP算法的流程:
假设现在文本串S匹配到 i 的位置,模式串P匹配到 j 的位置
(1)如果j==-1 或者 S[ i ]==p[ j ],就 i++,j++,继续匹配下一个字符
(2)如果 j != -1 && 当前的字符匹配失配,i不变(即 i 不回溯),j = next [ j ],模式串向右移动了 j-next[ j ]位。
整个算法最坏的情况是:当模式串的首字符位于i-j的位置时才匹配成功
如果文本穿的长度为n,模式串的长度为m,匹配过程的时间复杂度是O(n),求解next数组是O(m),KMP算法的复杂度是O(m+n)。
有错的话,请大家及时指正!!!
参考文献:
1、 从头到尾彻底理解KMP(2014年8月22日版)
2、从头到尾彻底理解KMP(2014年7月版)
3、《数据结构(C语言版)》,李云清 杨庆红 揭安全编著
4、KMP算法(1):如何理解KMP
相关文章:
框架页面jquery装载
转载于:https://www.cnblogs.com/moonsoft/p/10313309.html

NDKJNI Android 相关资料整理(四)
JNI/NDK开发指南 JNI/NDK开发指南(一)—— JNI开发流程及HelloWorld http://blog.csdn.net/xyang81/article/details/41777471 JNI/NDK开发指南(二)——JVM查找java native方法的规则 http://blog.csdn.net/xyang81/article/det…

【ACM】与全排列相关的STL函数 prev_permutation next_permutation
排列 与 全排列 从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。 当mn时所有的排列情况叫全排列。如果这组数有n个,那么全排列数为n!个。 对于全排列的求解…

虚拟机无法使用网卡桥接模式
重装了好几遍操作系统,换了两个虚拟机,差点怀疑人生…… 最终的原因竟然是win10!!! 1.执行WINR 输入services.msc,打开服务管理器(回车)。 2.找到Device Install Service服务 启动此…

Azure自动化部署运维浅谈
本次来谈一谈如何在Azure中实现一些简单的自动化运维的需求,一般来讲自动化运维我们通过很多第三方的工具平台实现,比较流行的目前有很多,比如老牌的chef, puppet,新兴的PowerShell DSC, ansible。这些应该都是耳熟能详的了。那么在Azure平台…
NDK/JNI demo ( 五 ) ORB_SLAM2在Android上的移植过程
Android平台搭建和NDK环境配置 Android移植基础 NDK是集成的Android中调用C代码的工具包,核心是JNI(Java Native Interface)技术,具体这里略过不表。只说说NDK开发的基本步骤: 1. 编写Java代码:在Java中定义…

[Nancy On .Net Core Docker] 轻量级的web框架
.net core现在已经有了大的发展,虽然笔者现在已经从事python开发,但是一直在关注.net的发展,在逛博客园的时候,发现有大家都会提到Nancy这个框架,在简单的使用之后,发现竟然是如此的简单而优雅 public clas…

【算法】【ACM】深入理解Dijkstra算法(单源最短路径算法)
Dijkstra算法是用来求解从某个源点到其他各顶点的最短路径(单源最短路径)。 下面的Dijkstra算法的讲解都是基于这个有向图,在遇到其他问题可以类比。 算法的基本思想: 把图中的定点分成两组,第一组包括已确定最短路径…

智能POS常见问题整理
智能POS预警值为小于所设的数量,H5就会变为锁定状态 智能POS查看数据库方法: 商米D1:设置-存储设备和USB-内部存储设备-浏览-winboxcash tablet.db为智能POS数据库 Winbox文件夹内,为相应logcat文件,应用出现问题时&am…

解决安卓系统写入SD卡权限问题
1.需要用户手动赋予的权限( Dangerous Permissions) 所属权限组权限日历READ_CALENDAR日历WRITE_CALENDAR相机CAMERA联系人READ_CONTACTS联系人WRITE_CONTACTS联系人GET_ACCOUNTS位置ACCESS_FINE_LOCATION位置ACCESS_COARSE_LOCATION麦克风RECORD_AUDIO…

【ACM】【STL】stack应用
C Stacks(堆栈) C Stack(堆栈) 是一个容器类的改编,为程序员提供了堆栈的全部功能,——也就是说实现了一个先进后出(FILO)的数据结构。 操作比较和分配堆栈empty()堆栈为空则返回真…

CHUCK手把手带你搞定OPENSTACK
以下是原文链接:http://blog.oldboyedu.com/openstack/转载于:https://blog.51cto.com/bovin/1858198

JVM基础面试题及原理讲解
2019独角兽企业重金招聘Python工程师标准>>> 本文从 JVM 结构入手,介绍了 Java 内存管理、对象创建、常量池等基础知识,对面试中 JVM 相关的基础题目进行了讲解。 写在前面(常见面试题) 基本问题 介绍下 Java 内存区域…

SLAM前端 ---------特征提取之ORB(ORB与SIFT与SURF)
ORB 论文翻译: 一种特征匹配替代方法:对比SIFT或SURF 1.ORB特征简介 ORB是Oriented FAST and Rotated BRIEF(oFAST and rBRIEF)的简称,ORB的名字已经说明了其来源,其实ORB特征是采用FAST方法来检测提取特…

oracle 内存分配和调优 总结
一直都想总结一下oracle内存调整方面的知识,最近正好优化一个数据库内存参数,查找一些资料并且google很多下。现在记录下来,做下备份。 一、概述: oracle 的内存可以按照共享和私有的角度分为系统全局区…

【ACM】Doubly Linked List(STL list)
题目链接:https://vjudge.net/problem/Aizu-ALDS1_3_C 这一题一开始的时候想的是用vector,超时 #include <iostream> #include <stack> #include <cstdio> #include <cstring> #include <queue> #include <vector>…

IOS获取焦点页面上移问题
var u navigator.userAgent; var flag; var myFunction; var isIOS !!u.match(/(i1;( U;)? CPU.Mac OS X/); if (isIOS) { document.body.addEventListener(focusin, () > { //软键盘弹起事件flag true;clearTimeout(myFunction); }) document.body.addEventListener(f…
SLAM之特征匹配(二)————RANSAC--------翻译以及经典RANSAC以及其相关的改进的算法小结
本文翻译自维基百科,英文原文地址是:http://en.wikipedia.org/wiki/ransac RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数…

【ACM】树 小结
树是一种表达层级结构的数据结构,也是实现高效算法与数据结构的基础。 学习之前的基础:数组,循环处理,结构体,递归函数。 树:由结点(node)和连接结点的边(edge…

【cocos2d-js官方文档】九、cc.loader
概述 原来的cc.Loader被改造为一个单例cc.loader,采用了插件机制设计,让loader做更纯粹的事。 各种资源类型的loader可以在外部注册进来,而不是直接将所有的代码杂揉在cc.Loader中,更好的方便管理以及用户自定义loader的创建。 cc…

更换VC后DDC提示证书不可用
问题描述:客户环境由Windows VC更换成Linux VC后,DDC提示证书不可用问题原因:因为VC更换后,存储在DDC数据库HostingUnitServiceSchema.HypervisorConnectionSSLThumbprint表中证书指纹信息和新得VC证书指纹信息不匹配。解决方法&a…

尺度空间理论与图像金字塔
我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性。也就是说使用卷积就是为了提取显著特征,减少特征维数,减少计算量。 在对图像进行卷积操作后的只管现象:图像变得模糊了,可是我们依然能够分辨出是什么&#x…

【ACM】 multiset 的 一些应用
一、The kth great number 题目链接:https://vjudge.net/problem/HDU-4006 用set写超时 (在VJ里,用C显示Compilation Error,选择G,则是TLE) #include <iostream> #include <set> #include &…

apache2.2 做后端,增加真实ip到日志中
apache2.2使用mod_remoteip模块 一.安装 wget https://github.com/ttkzw/mod_remoteip-httpd22/raw/master/mod_remoteip.c/usr/local/apache/bin/apxs -i -c -n mod_remoteip.so mod_remoteip.c 二.添加Apache配置vi /usr/local/apache/conf/httpd.confInclude conf/extra/htt…

高可用方案系统架构
2019独角兽企业重金招聘Python工程师标准>>> 高可用方案 系统架构 转载于:https://my.oschina.net/qiongtaoli/blog/3007587

OpenCV3.2.0+VS2017在window10开发环境配置记录
本机环境:win10 64位 OpenCV3.2.0 Visual Studio 2017 最后结果,亲测可用OpenCV官方下载地址: http://opencv.org/releases.html#本人选择opencv3.2.0基于Windows平台。读者根据自己需要选择合适版本及平台下载。 选择window版本的opencv下载…
C++vector迭代器失效的问题
转载:http://blog.csdn.net/olanmomo/article/details/38420907 转载:http://blog.csdn.net/stpeace/article/details/46507451 转载:http://www.cnblogs.com/xkfz007/articles/2509433.html 转载:http://www.cnblogs.com/BeyondAnyTime/archive/2012/08/13/2636375.html 有这样…

【HDU】1251统计难题 (字典树:二维数组,结构体数组,链表,map)
使用二维数组或者结构体数组都可以,但是在计数的时候有一点点小区别 一、结构体数组 #include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <string> typedef long long ll; using namespace…
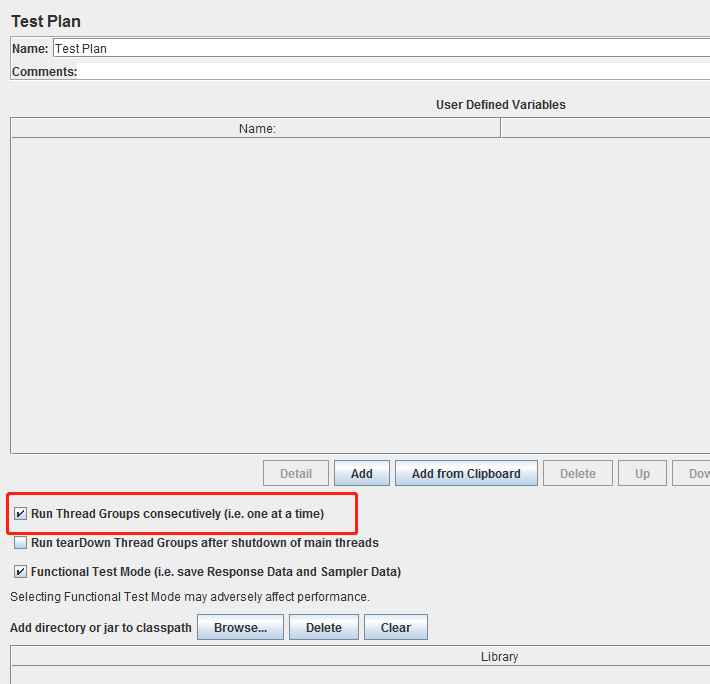
Jmeter干货 不常用却极其有用的几个地方
1. Jmeter测试计划下Run Thread Groups consecutively 表示序列化执行测试计划下所有线程组中的各个请求 如下图配置,新建的测试计划中,不默认勾选此项, 而享用Jmeter做接口自动化测试的同学们,会发现一个问题是,可能多…

图像滤波总结(面试经验总结)
目录 图像平滑处理,6种滤波总结的综合示例 【盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波导向滤波】 1-图像滤波 2-代码演示 3-显示结果 4-程序说明 5 角点检测(Harris,Fast,surf) 图像平滑处理,6种滤波总结的综合示…