【算法】【ACM】深入理解Dijkstra算法(单源最短路径算法)
Dijkstra算法是用来求解从某个源点到其他各顶点的最短路径(单源最短路径)。

下面的Dijkstra算法的讲解都是基于这个有向图,在遇到其他问题可以类比。
算法的基本思想:
把图中的定点分成两组,第一组包括已确定最短路径的顶点,初始时只含有一个源点,记为集合S;第二组包括尚未确定的最短路径的顶点,记为V-S;按最短路径长度递增的顺序逐个把V-S中的顶点加到S中去,直至从v0出发可以到达的所有顶点都包括在S中。
【讲到这里要打断一下:我最初就是不能理解这个“按最短路径长度的递增顺序”(1)这个顺序到底是什么顺序?(2)哪个点到哪个点的最短路径长度?(3)如果是那个已经确定的源点到其他点的最短路径,但是源点并不是到每个点都有路径,在开始给邻接矩阵复制的时候,有的位置是INF,那这个怎么比较????当时心里有无数个问号,找了很多博客,大家都没有详细说明(内心:这个这么好理解?我这么弱?)下面就会一一解答上面的问号。】
接着上面,在这个过程中,总保持v0到第一组S中各顶点的最短路径都不大(小于等于)与v0到第二组V-S的任何顶点的最短路径长度,第二组的顶点对应距离值是从v0到此顶点的只包括第一组S的顶点中为中间顶点的最短路径长度。对于S中任意一点 j,v0到j的路径长度皆小于v0到V-S中任意一点的路径长度。(这也与上面用红色标注的按照最短路径长度的递增顺序)
| 始点 | 终点 | 最短路径 | 路径长度 |
| A | B | (A,C,B) | 19 |
| C | (A,C) | 4 | |
| D | (A,C,F,D) | 25 | |
| E | (A,C,B,E) | 29 | |
| F | (A,C,F) | 12 |
 该表格表示:A到其余各点的最短路径
该表格表示:A到其余各点的最短路径
看到这里:上述所说的按照对端路径长度的递增顺序逐个把V-S中的顶点加到S中去,但是在拿到一个有向图时,我们怎么可能一眼看出路径长度是多少?需要代码求解。
为了实现该串代码,与要设置需要设置距离向量d[ ](即:源点到该点的最短路径),以及保存路径的向量p[](即:它的前一个点是谁(官方:最短路径上第i个顶点的前驱顶点序号))。
算法的具体步骤可描述如下:
(1)初始化:包括对第一组(集合S:目前集合S只有{v0})的初始化与对距离向量d的初始化(用邻接矩阵中相应的值进行赋值)。
(2)从第二组V-S的顶点中选取一个距离值最小的顶点v加入S,。接着对V-S中的所有顶点值进行修改,修改的方法是,对于V-S中的任意一个顶点k,若图中有边<v,k>,且v0到v的距离加上<v,k>边上的权值之和小于v0到k的距离值,则用“v0到v的距离加上<v,k>边上的权值代替顶点k原来的距离值”,(v作为中间点);反之,则顶点k的距离值保持不变。
。
【我的理解:就是一开始d[k]中肯定就和邻接矩阵中的值一样,有数字,也有INF(即不存在到该点的路径,但是随着S集合中不断加入顶点(按照最短路径的长度递增顺序),源点通过加入的这些顶点就可以到达更多的顶点,每加入一个顶点,就要算一下通过这个刚刚加入的中间点,v0到其他点的距离是否有变短,如果有,则修改相应的值,反之,则保持不变。要保证加入到S中的每个点,源点v0到它们的路径长度是最短的。】
(3)若集合V-S已空,则结束算法。若V-S不为空,则返回步骤(2)。
有向网G采用邻接矩阵存储结构
#include <stdio.h>
#include <stdlib.h>
#define M 20
#define FINITY 50000
typedef struct
{char vexs[M];int edges[M][M];int n,e;
}Mgraph;创建网络的邻接矩阵算法
void creat(Mgraph *g,int c)
{int i,j,k,w;FILE *f;f=fopen("test.txt","r");if(f){fscanf(f,"%d%d",&g->n,&g->e);for(i=0;i<g->n;i++)fscanf(f,"%1s",&g->vexs[i]);for(i=0;i<g->n;i++){for(j=0;j<g->n;j++){if(i==j) g->edges[i][j]=0;else g->edges[i][j]=FINITY;}}for(k=0;k<g->e;k++){fscanf(f,"%d%d%d",&i,&j,&w);g->edges[i][j]=w;if(c==0) g->edges[j][i]=w;}fclose(f);}else{g->n=0;}
}输出邻接矩阵
void print(Mgraph g)
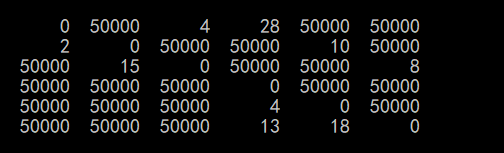
{printf("\n");for(int i=0;i<g.n;i++){for(int j=0;j<g.n;j++){printf("%7d",g.edges[i][j]);}printf("\n");}
}这里图中显示的 “50000” 即为 INF
Dijkstra算法代码实现
void dijkstra1(Mgraph g,int v0)
{print(g);int i,j,k,v,min,x;//第一步:初始化集合S与距离向量dfor(v=0;v<g.n;v++){vis[v]=0;d[v]=g.edges[v0][v];//d[v]==0 则是edges[i][j]中i==j的情况//d[v]==FINITY 则是v0和v之间没有路径可达if(d[v]<FINITY && d[v]!=0)p[v]=v0;elsep[v]=-1;//没有前驱结点}vis[v0]=1;d[v0]=0;//初始时集合S中只有一个v0printf("\n初始d[]数组:\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);//第二步:依次找出n-1个结点加入S中for(i=1;i<g.n;i++){min=FINITY;for(k=0;k<g.n;k++){//在d[k]中找出没有被选入S集合中的,距离v0最近的点//这就体现了“按照最短路径长度的递增顺序”if(!vis[k] && d[k]<min){v=k;min=d[k];}}//输出此次被选入的顶点距离printf("\n%c %d\n",g.vexs[v],min);if(min==FINITY) return ;vis[v]=1;//已经被选进入集合S//第三步:修改S与V-S中各结点的距离for(k=0;k<g.n;k++){if(!vis[k] && (min+g.edges[v][k])<d[k]){d[k]=min+g.edges[v][k];p[k]=v;}}//这里是输出每一次数组d[],可以清楚观察d[]中各元素的变化情况printf("*********\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);printf("*********\n");}printf("\n最终d[]数组:\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);
}
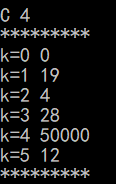
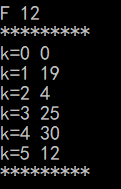
初始状态就是因为选择的是v0(A结点:序号0),所以和邻接矩阵第一行一样。
C F B D E 是依次加入集合S顺序
vis[0]已经被标记为1了
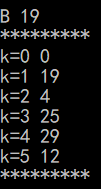
i=1:找到的v=2,min=4,vis[2]=1
接着比较通过顶点2(C)到其他结点的距离是否有改变
min+g.edges[2][1]=4+15=19<INF ,所以d[1]=19
min+fg.edges[2][5]=4+8=12<INF,所以d[5]=12(就是第二张图的情况)
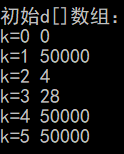
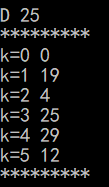
i=2:v=5,min=12,vis[5]=1
接着比较通过顶点5(F)到其他结点的距离是否有改变
min+g.edges[5][3]=12+13=25,所以k[3]=25
min+g,edges[5][4]=12+18=30,所以k[4]=30(就是第三张图的情况)
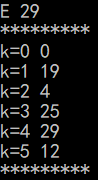
。。。。。。
以此类推,大家可以结合图自己算一下。
对应着图来比较 “原来源点到某一点的距离”与“源点到新加入S的这个点的距离+这个点到图中某一点的距离”是否有缩短。最终的d[ ]数组就是顶点A到各个点的最短距离。
这里只是举了d[ ]数组,p[ ]数组也是一样。
全部代码
#include <stdio.h>
#include <stdlib.h>
#define M 20
#define FINITY 50000
typedef struct
{char vexs[M];int edges[M][M];int n,e;
}Mgraph;void creat(Mgraph *g,int c)
{int i,j,k,w;FILE *f;f=fopen("test.txt","r");if(f){fscanf(f,"%d%d",&g->n,&g->e);for(i=0;i<g->n;i++)fscanf(f,"%1s",&g->vexs[i]);for(i=0;i<g->n;i++){for(j=0;j<g->n;j++){if(i==j) g->edges[i][j]=0;else g->edges[i][j]=FINITY;}}for(k=0;k<g->e;k++){fscanf(f,"%d%d%d",&i,&j,&w);g->edges[i][j]=w;if(c==0) g->edges[j][i]=w;}fclose(f);}else{g->n=0;}
}void print(Mgraph g)
{printf("\n");for(int i=0;i<g.n;i++){for(int j=0;j<g.n;j++){printf("%7d",g.edges[i][j]);}printf("\n");}
}
int vis[M];//表示当前元素是否已求出最短路径
int p[M];//路径向量
int d[M];//距离向量
void dijkstra1(Mgraph g,int v0)
{print(g);int i,j,k,v,min,x;//第一步:初始化集合S与距离向量dfor(v=0;v<g.n;v++){vis[v]=0;d[v]=g.edges[v0][v];//d[v]==0 则是edges[i][j]中i==j的情况//d[v]==FINITY 则是v0和v之间没有路径可达if(d[v]<FINITY && d[v]!=0)p[v]=v0;elsep[v]=-1;//没有前驱结点}vis[v0]=1;d[v0]=0;//初始时集合S中只有一个v0printf("\n初始d[]数组:\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);//第二步:依次找出n-1个结点加入S中for(i=1;i<g.n;i++){min=FINITY;for(k=0;k<g.n;k++){//在d[k]中找出没有被选入S集合中的,距离v0最近的点//这就体现了“按照最短路径长度的递增顺序”if(!vis[k] && d[k]<min){v=k;min=d[k];}}//输出此次被选入的顶点距离printf("\n%c %d\n",g.vexs[v],min);if(min==FINITY) return ;vis[v]=1;//已经被选进入集合S//第三步:修改S与V-S中各结点的距离for(k=0;k<g.n;k++){if(!vis[k] && (min+g.edges[v][k])<d[k]){d[k]=min+g.edges[v][k];p[k]=v;}}//这里是输出每一次数组d[],可以清楚观察d[]中各元素的变化情况printf("*********\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);printf("*********\n");}printf("\n最终d[]数组:\n");for(k=0;k<g.n;k++)printf("k=%d %d\n",k,d[k]);
}int main ()
{Mgraph g;creat(&g,1);dijkstra1(g,0);return 0;
}这是数据结构中的代码,与一般ACM题目中的代码大同小异,下面就举几个例题,来亲自实践一下
现学活用
一、杭电OJ 3790 最短路径问题
http://acm.hdu.edu.cn/showproblem.php?pid=3790
套用上面Dijkstra算法的模板,加上一点点小的改动,上面的代码针对的时有向图,这道题无向图,所以赋值的时候要注意,还有引入了花费,不止问最短路径,在判断上需要注意一下
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 1000;
const int FINITY = 500000;
int map[1010][1010];
int price[1010][1010];
int dis[1010],p1[1010];
int vis[1010];
int n,m,a,b,d,s,t,p;
void dijkstra()
{int i,j,k,min,v;for(i=1;i<n;i++){min=FINITY;for(k=1;k<=n;k++){if(!vis[k] && min>dis[k]){min=dis[k];v=k;}}vis[v]=1;for(k=1;k<=n;k++){if(!vis[k] && (min+map[v][k])<dis[k]){dis[k]=min+map[v][k];p1[k]=p1[v]+price[v][k];}else if(dis[k]==min+map[v][k]){if(p1[k]>p1[v]+price[v][k])p1[k]=p1[v]+price[v][k];}}}
}int main ()
{int i,j;while(scanf("%d%d",&n,&m)!=EOF){if(m==0 && n==0) break;for(i=0;i<=n;i++){for(j=0;j<=n;j++){if(i==j) {map[i][j]=0;price[i][j]=0;}else {map[i][j]=FINITY;price[i][j]=FINITY;}}}for(int q=0;q<m;q++){scanf("%d%d%d%d",&a,&b,&d,&p);if(d<map[a][b]){map[a][b]=d;map[b][a]=d;price[a][b]=p;price[b][a]=p;}}memset(vis,0,sizeof(vis));scanf("%d%d",&s,&t);vis[s]=1;for(i=1;i<=n;i++){dis[i]=map[s][i];p1[i]=price[s][i];}dijkstra();printf("%d %d\n",dis[t],p1[t]);}return 0;
}二、杭电OJ 2544 最短路
http://acm.hdu.edu.cn/showproblem.php?pid=2544
这一题就是完全套用模板,模板里还有一个路径向量p,这个题不需要用到路径向量p,所以相比较上一题来说比较简单
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int INF = 5000000;
int map[105][105];
int dis[105];
int vis[105];
int N,M;void dijkstra()
{int i,j,min,v;for(i=1;i<N;i++){min=INF;for(j=1;j<=N;j++){if(!vis[j] && dis[j]<min){min=dis[j];v=j;}}vis[v]=1;for(j=1;j<=N;j++){if(!vis[j] && (min+map[v][j])<dis[j]){dis[j]=min+map[v][j];}}}
}int main ()
{int i,j,a,b,t;while(scanf("%d%d",&N,&M)!=EOF){if(N==0 && M==0) return 0;for(i=0;i<=N;i++){for(j=0;j<=N;j++){if(i==j) map[i][j]=0;else map[i][j]=INF;}}for(i=0;i<M;i++){scanf("%d%d%d",&a,&b,&t);if(t < map[a][b]){map[a][b]=t;map[b][a]=t;}}memset(vis,0,sizeof(vis));for(i=1;i<=N;i++)dis[i]=map[1][i];vis[1]=1;dijkstra();printf("%d\n",dis[N]);}return 0;
}三、杭电OJ 1874 畅通工程续
这个题目是存在可能找不到最短路径的情况,所以需要在最后判断dis[t]的值是否为INF,是的话就不存在,不是的话就输出它的值。
http://acm.hdu.edu.cn/showproblem.php?pid=1874
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int INF = 500000;
int map[205][205];
int dis[205];
int vis[205];
int n,m,a,b,x,s,t;
void dijkstra()
{int i,j,min,v;for(i=1;i<n;i++){min=INF;for(j=0;j<n;j++){if(!vis[j] && min > dis[j]){min=dis[j];v=j;}}if(min==INF) return ;vis[v]=1;for(j=0;j<n;j++){if(!vis[j] && (min+map[v][j])<dis[j]){dis[j]=min+map[v][j];}}}
}int main ()
{int i,j;while(scanf("%d%d",&n,&m)!=EOF){for(i=0;i<=n;i++){for(j=0;j<=n;j++){if(i==j) map[i][j]=0;else map[i][j]=INF;}}for(i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&x);if(x < map[a][b]){map[a][b]=x;map[b][a]=x;}}scanf("%d%d",&s,&t);memset(vis,0,sizeof(vis));for(i=0;i<n;i++)dis[i]=map[s][i];vis[s]=1;dijkstra();if(dis[t]==INF)printf("-1\n");elseprintf("%d\n",dis[t]);}return 0;
}四、POJ 2387 Til the Cows Come Home
http://poj.org/problem?id=2387
这个题最重要的就是读懂题意,看清楚哪个字母代表点的数目,哪个字母是边的数目,数组要开的足够大,不然会Runtime Error
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int INF = 0xfffffff;
int map[1010][1010];
int dis[1010];
int vis[1010];
int n,m,a,b,x,s,t;
void dijkstra()
{int i,j,min,v;for(i=1;i<n;i++){min=INF;for(j=1;j<=n;j++){if(!vis[j] && min > dis[j]){min=dis[j];v=j;}}if(min==INF) break;vis[v]=1;for(j=1;j<=n;j++){if(!vis[j] && (min+map[v][j])<dis[j]){dis[j]=min+map[v][j];}}}
}int main ()
{int i,j;while(scanf("%d%d",&m,&n)!=EOF){for(i=0;i<=n;i++){for(j=0;j<=n;j++){if(i==j) map[i][j]=0;else map[i][j]=INF;}}for(i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&x);if(x < map[a][b] && x){map[a][b]=x;map[b][a]=x;}}memset(vis,0,sizeof(vis));for(i=1;i<=n;i++)dis[i]=map[1][i];vis[1]=1;dijkstra();printf("%d\n",dis[n]);}return 0;
}从上面四道题可以看出,运用Dijkstra算法时,就是套用模板,但是一定要清楚Dijkstra算法的步骤及其内涵,才能运用自如,我现在也不敢说我完全掌握了Dijkstra算法,需要反复地揣摩,做一些题进行复习,有错的地方希望大家及时指正!!!谢谢
相关文章:

智能POS常见问题整理
智能POS预警值为小于所设的数量,H5就会变为锁定状态 智能POS查看数据库方法: 商米D1:设置-存储设备和USB-内部存储设备-浏览-winboxcash tablet.db为智能POS数据库 Winbox文件夹内,为相应logcat文件,应用出现问题时&am…

解决安卓系统写入SD卡权限问题
1.需要用户手动赋予的权限( Dangerous Permissions) 所属权限组权限日历READ_CALENDAR日历WRITE_CALENDAR相机CAMERA联系人READ_CONTACTS联系人WRITE_CONTACTS联系人GET_ACCOUNTS位置ACCESS_FINE_LOCATION位置ACCESS_COARSE_LOCATION麦克风RECORD_AUDIO…

【ACM】【STL】stack应用
C Stacks(堆栈) C Stack(堆栈) 是一个容器类的改编,为程序员提供了堆栈的全部功能,——也就是说实现了一个先进后出(FILO)的数据结构。 操作比较和分配堆栈empty()堆栈为空则返回真…

CHUCK手把手带你搞定OPENSTACK
以下是原文链接:http://blog.oldboyedu.com/openstack/转载于:https://blog.51cto.com/bovin/1858198

JVM基础面试题及原理讲解
2019独角兽企业重金招聘Python工程师标准>>> 本文从 JVM 结构入手,介绍了 Java 内存管理、对象创建、常量池等基础知识,对面试中 JVM 相关的基础题目进行了讲解。 写在前面(常见面试题) 基本问题 介绍下 Java 内存区域…

SLAM前端 ---------特征提取之ORB(ORB与SIFT与SURF)
ORB 论文翻译: 一种特征匹配替代方法:对比SIFT或SURF 1.ORB特征简介 ORB是Oriented FAST and Rotated BRIEF(oFAST and rBRIEF)的简称,ORB的名字已经说明了其来源,其实ORB特征是采用FAST方法来检测提取特…

oracle 内存分配和调优 总结
一直都想总结一下oracle内存调整方面的知识,最近正好优化一个数据库内存参数,查找一些资料并且google很多下。现在记录下来,做下备份。 一、概述: oracle 的内存可以按照共享和私有的角度分为系统全局区…

【ACM】Doubly Linked List(STL list)
题目链接:https://vjudge.net/problem/Aizu-ALDS1_3_C 这一题一开始的时候想的是用vector,超时 #include <iostream> #include <stack> #include <cstdio> #include <cstring> #include <queue> #include <vector>…

IOS获取焦点页面上移问题
var u navigator.userAgent; var flag; var myFunction; var isIOS !!u.match(/(i1;( U;)? CPU.Mac OS X/); if (isIOS) { document.body.addEventListener(focusin, () > { //软键盘弹起事件flag true;clearTimeout(myFunction); }) document.body.addEventListener(f…
SLAM之特征匹配(二)————RANSAC--------翻译以及经典RANSAC以及其相关的改进的算法小结
本文翻译自维基百科,英文原文地址是:http://en.wikipedia.org/wiki/ransac RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数…

【ACM】树 小结
树是一种表达层级结构的数据结构,也是实现高效算法与数据结构的基础。 学习之前的基础:数组,循环处理,结构体,递归函数。 树:由结点(node)和连接结点的边(edge…

【cocos2d-js官方文档】九、cc.loader
概述 原来的cc.Loader被改造为一个单例cc.loader,采用了插件机制设计,让loader做更纯粹的事。 各种资源类型的loader可以在外部注册进来,而不是直接将所有的代码杂揉在cc.Loader中,更好的方便管理以及用户自定义loader的创建。 cc…

更换VC后DDC提示证书不可用
问题描述:客户环境由Windows VC更换成Linux VC后,DDC提示证书不可用问题原因:因为VC更换后,存储在DDC数据库HostingUnitServiceSchema.HypervisorConnectionSSLThumbprint表中证书指纹信息和新得VC证书指纹信息不匹配。解决方法&a…

尺度空间理论与图像金字塔
我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性。也就是说使用卷积就是为了提取显著特征,减少特征维数,减少计算量。 在对图像进行卷积操作后的只管现象:图像变得模糊了,可是我们依然能够分辨出是什么&#x…

【ACM】 multiset 的 一些应用
一、The kth great number 题目链接:https://vjudge.net/problem/HDU-4006 用set写超时 (在VJ里,用C显示Compilation Error,选择G,则是TLE) #include <iostream> #include <set> #include &…

apache2.2 做后端,增加真实ip到日志中
apache2.2使用mod_remoteip模块 一.安装 wget https://github.com/ttkzw/mod_remoteip-httpd22/raw/master/mod_remoteip.c/usr/local/apache/bin/apxs -i -c -n mod_remoteip.so mod_remoteip.c 二.添加Apache配置vi /usr/local/apache/conf/httpd.confInclude conf/extra/htt…

高可用方案系统架构
2019独角兽企业重金招聘Python工程师标准>>> 高可用方案 系统架构 转载于:https://my.oschina.net/qiongtaoli/blog/3007587

OpenCV3.2.0+VS2017在window10开发环境配置记录
本机环境:win10 64位 OpenCV3.2.0 Visual Studio 2017 最后结果,亲测可用OpenCV官方下载地址: http://opencv.org/releases.html#本人选择opencv3.2.0基于Windows平台。读者根据自己需要选择合适版本及平台下载。 选择window版本的opencv下载…
C++vector迭代器失效的问题
转载:http://blog.csdn.net/olanmomo/article/details/38420907 转载:http://blog.csdn.net/stpeace/article/details/46507451 转载:http://www.cnblogs.com/xkfz007/articles/2509433.html 转载:http://www.cnblogs.com/BeyondAnyTime/archive/2012/08/13/2636375.html 有这样…

【HDU】1251统计难题 (字典树:二维数组,结构体数组,链表,map)
使用二维数组或者结构体数组都可以,但是在计数的时候有一点点小区别 一、结构体数组 #include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <string> typedef long long ll; using namespace…
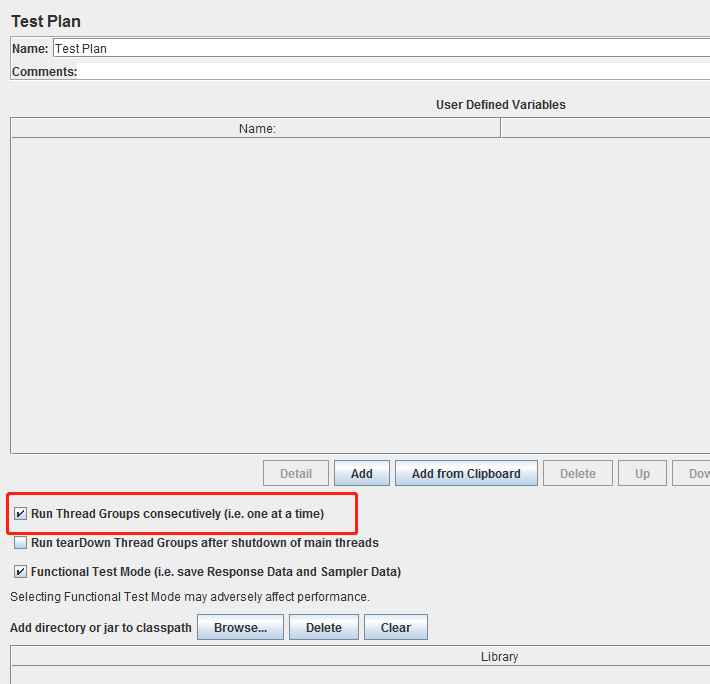
Jmeter干货 不常用却极其有用的几个地方
1. Jmeter测试计划下Run Thread Groups consecutively 表示序列化执行测试计划下所有线程组中的各个请求 如下图配置,新建的测试计划中,不默认勾选此项, 而享用Jmeter做接口自动化测试的同学们,会发现一个问题是,可能多…

图像滤波总结(面试经验总结)
目录 图像平滑处理,6种滤波总结的综合示例 【盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波导向滤波】 1-图像滤波 2-代码演示 3-显示结果 4-程序说明 5 角点检测(Harris,Fast,surf) 图像平滑处理,6种滤波总结的综合示…

【小贴士】DEV 多行注释
多行注释 Ctrl / 取消多行注释 Ctrl ,

JSP+Servlet基础一
2019独角兽企业重金招聘Python工程师标准>>> JSP中的指令: 格式:<%指令的名称(page,taglib,include...) 属性属性值%> 指令中的page:用于整个页面,定义与页面相关的属性。page属性一共有13个。 1、常…

Chameleon跨端框架——壹个理想主义团队的开源作品
文章较长,信息量很大,请耐心阅读,必然有收获。下面正文开始~背景解决方案原理久经考验生产应用举例易用性好多态协议学习成本低渐进式接入业内对比后期规划理想主义历经近20个月打磨,滴滴跨端方案chameleon终于开源了github.com/d…

尺度空间理论与图像金字塔(二)
SIFT简介 整理一下方便阅读,作者写的东西摘自论文,在此感谢xiaowei等的贡献 DoG尺度空间构造(Scale-space extrema detection)http://blog.csdn.net/xiaowei_cqu/article/details/8067881关键点搜索与定位(Keypoint l…

仿桌面通知pnotify插件
在做网站的时候,alert弹出框是非常常见的情形。但是,有些情况下,弹框对用户来说是并不友好的。调研了几个其他的提示插件了,发现pnotify比较好用,可配置性也高。 使用示例: <!DOCTYPE html> <html…

【HDU】1305 Immediate Decodability(字典树:结构体数组,二维数组,链表/指针)
一、用的二维数组 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int maxn 100; int tr[maxn][2]; int mk[maxn]; int tot;void insert(string s) {int u 0;for(int i0;i<s.length();i){int x s[i]-0;if(tr…

Hyperledger Grid:一个用于分布式供应链解决方案的框架
Hyperledger在最近的一篇博文中发布了一个名为Hyperledger Grid的新项目。Grid是一个用于集成分布式账本技术(DLT)解决方案与供应链行业企业业务系统的框架。该项目提供了一个参考架构、通用数据模型和智能合约,所有这些都是基于开放标准和行…

尺度不变特征变换匹配算法详解
尺度不变特征变换匹配算法详解Scale Invariant Feature Transform(SIFT)Just For Fun对于初学者,从David G.Lowe的论文到实现,有许多鸿沟,本文帮你跨越。1、SIFT综述 尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视…