SLAM之特征匹配(二)————RANSAC--------翻译以及经典RANSAC以及其相关的改进的算法小结
本文翻译自维基百科,英文原文地址是:http://en.wikipedia.org/wiki/ransac
RANSAC是“RANdom SAmple Consensus(随机抽样一致)”的缩写。它可以从一组包含“局外点”的观测数据集中,通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果;为了提高概率必须提高迭代次数。该算法最早由Fischler和Bolles于1981年提出。他们使用该算法来解决3D重建中的位置确定问题(Location Determination Problem, LDP)。目前RANSAC算法被广泛用于计算机视觉领域中图像匹配、全景拼接等问题,比如从数对匹配的特征点中求得两幅图片之间的射影变换矩阵,OPENCV实现stitching类时即使用了该算法。
RANSAC算法与最小二乘法的不同之处主要有以下两点:
1. 最小二乘法总是使用所有的数据点来估计参数,而RANSAC算法仅使用局内点;
2. 最小二乘法是一种确定性算法,给定数据集,每一次所得到的模型参数都是相同的;而RANSAC算法是一种随机算法,受迭代次数等的影响,每一次得到的参数一般都不相同。
3. 一般而言,RANSAC算法先根据一定的准则筛选出局内点和局外点,然后对得到的局内点进行拟合,拟合方法可以是最小二乘法,也可以是其他优化算法,从这个角度来说,RANSAC算法是最小二乘法的扩展。
RANSAC的基本假设是:
(1)数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
(2)“局外点”是不能适应该模型的数据;
(3)除此之外的数据属于噪声。
局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设。
RANSAC也做了以下假设:给定一组(通常很小的)局内点,存在一个可以估计模型参数的过程;而该模型能够解释或者适用于局内点。
算法的求解过程如下:
- 首先从数据集中随机选出一组局内点(其数目要保证能够求解出模型的所有参数),计算出一套模型参数。
- 用得到的模型去测试其他所有的数据点,如果某点的误差在设定的误差阈值之内,就判定其为局内点,否则为局外点,只保留目前为止局内点数目最多的模型,将其记录为最佳模型。
- 重复执行1,2步足够的次数(即达到预设的迭代次数)后,使用最佳模型对应的局内点来最终求解模型参数,该步可以使用最小二乘法等优化算法。
- 最后可以通过估计局内点与模型的错误率来评估模型。
本文内容
1 示例
2 概述
3 part1 算法
3 part2算法实例
4 参数
5 优点与缺点
6 应用
7 参考文献
8 外部链接
一、示例
一个简单的例子是从一组观测数据中找出合适的2维直线。假设观测数据中包含局内点和局外点,其中局内点近似的被直线所通过,而局外点远离于直线。简单的最小二乘法不能找到适应于局内点的直线,原因是最小二乘法尽量去适应包括局外点在内的所有点。相反,RANSAC能得出一个仅仅用局内点计算出模型,并且概率还足够高。但是,RANSAC并不能保证结果一定正确,为了保证算法有足够高的合理概率,我们必须小心的选择算法的参数。
左图:包含很多局外点的数据集 右图:RANSAC找到的直线(局外点并不影响结果)
二、概述
RANSAC算法的输入是一组观测数据,一个可以解释或者适应于观测数据的参数化模型,一些可信的参数。
RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点,并用下述方法进行验证:
1.有一个模型适应于假设的局内点,即所有的未知参数都能从假设的局内点计算得出。
2.用1中得到的模型去测试所有的其它数据,如果某个点适用于估计的模型,认为它也是局内点。
3.如果有足够多的点被归类为假设的局内点,那么估计的模型就足够合理。
4.然后,用所有假设的局内点去重新估计模型,因为它仅仅被初始的假设局内点估计过。
5.最后,通过估计局内点与模型的错误率来评估模型。
这个过程被重复执行固定的次数,每次产生的模型要么因为局内点太少而被舍弃,要么因为比现有的模型更好而被选用。
三、part one 算法
伪码形式的算法如下所示:
输入:
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出:
best_model —— 跟数据最匹配的模型参数(如果没有找到好的模型,返回null)
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误
iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
maybe_inliers = 从数据集中随机选择n个点
maybe_model = 适合于maybe_inliers的模型参数
consensus_set = maybe_inliers
for ( 每个数据集中不属于maybe_inliers的点 )
if ( 如果点适合于maybe_model,且错误小于t )
将点添加到consensus_set
if ( consensus_set中的元素数目大于d )
已经找到了好的模型,现在测试该模型到底有多好
better_model = 适合于consensus_set中所有点的模型参数
this_error = better_model究竟如何适合这些点的度量
if ( this_error < best_error )
我们发现了比以前好的模型,保存该模型直到更好的模型出现
best_model = better_model
best_consensus_set = consensus_set
best_error = this_error
增加迭代次数
返回 best_model, best_consensus_set, best_error
RANSAC算法的可能变化包括以下几种:
(1)如果发现了一种足够好的模型(该模型有足够小的错误率),则跳出主循环。这样可能会节约计算额外参数的时间。
(2)直接从maybe_model计算this_error,而不从consensus_set重新估计模型。这样可能会节约比较两种模型错误的时间,但可能会对噪声更敏感。
三、part two算法实例
C++代码实现
Ziv Yaniv以最简单的直线拟合为例,写过一版RANSAC算法的C++实现,没有依赖任何其他库,但该版代码对C++的依赖较重,使用了C++的一些高级数据结构,比如vector, set,在遍历时还使用了递归算法。详细代码可参见RANSAC代码示例
部分代码及相关注释如下:
//顶层变量定义 vector<double> lineParameters;//存储模型参数 LineParamEstimator lpEstimator(0.5);//误差阈值设置为0.5 vector<Point2D> pointData;//数据点集 int numForEstimate=2;//进行一次参数估计所需的最小样本点数,因为是直线拟合,所以可以直接设为2//顶层函数的定义/*** Estimate the model parameters using the maximal consensus set by going over ALL possible* subsets (brute force approach).* Given: n - data.size()* k - numForEstimate* We go over all n choose k subsets n!* ------------* (n-k)! * k!* @param parameters A vector which will contain the estimated parameters.* If there is an error in the input then this vector will be empty.* Errors are: 1. Less data objects than required for an exact fit.* @param paramEstimator An object which can estimate the desired parameters using either an exact fit or a* least squares fit.* @param data The input from which the parameters will be estimated.* @param numForEstimate The number of data objects required for an exact fit.* @return Returns the percentage of data used in the least squares estimate.** NOTE: This method should be used only when n choose k is small (i.e. k or (n-k) are approximatly equal to n)**///T是数据的类型,该例子中是二维坐标点,作者自己定义了一个类Point2D来表示;S是参数的类型,此处为双精度double型 template <class T, class S> double Ransac<T, S>::compute(std::vector<S> ¶meters,ParameterEsitmator<T, S> *paramEstimator, std::vector<T> &data, int numForEstimate) {std::vector<T *> leastSquaresEstimateData;int numDataObjects = data.size();//数据集的大小,100int numVotesForBest = -1;//最佳模型所对应的局内点数目初始化为-1int *arr = new int[numForEstimate];//要进行一次计算所需的样本数:2 short *curVotes = new short[numDataObjects]; //one if data[i] agrees with the current model, otherwise zeroshort *bestVotes = new short[numDataObjects]; //one if data[i] agrees with the best model, otherwise zero//there are less data objects than the minimum required for an exact fitif (numDataObjects < numForEstimate)return 0;//computeAllChoices函数寻找局内点数目最多的模型,并将局内点信息存储在bestVotes数组中,作为最终的模型computeAllChoices(paramEstimator, data, numForEstimate,bestVotes, curVotes, numVotesForBest, 0, data.size(), numForEstimate, 0, arr);//将所有的局内点取出,存储在leastSquareEstimateData数组中 for (int j = 0; j<numDataObjects; j++) {if (bestVotes[j])leastSquaresEstimateData.push_back(&(data[j]));} //利用所有局内点进行最小二乘参数估计,估计的结果存储在parameters数组中paramEstimator->leastSquaresEstimate(leastSquaresEstimateData, parameters);//释放动态数组delete[] arr;delete[] bestVotes;delete[] curVotes; //返回值为局内点占所有数据点的比值return (double)leastSquaresEstimateData.size() / (double)numDataObjects; }//寻找最佳模型的函数定义如下: //使用递归算法来对数据集进行n!/((n-k)!k!)次遍历 template<class T, class S> void Ransac<T, S>::computeAllChoices(ParameterEsitmator<T, S> *paramEstimator, std::vector<T> &data, int numForEstimate,short *bestVotes, short *curVotes, int &numVotesForBest, int startIndex, int n, int k, int arrIndex, int *arr) {//we have a new choice of indexes//每次k从2开始递减到0的时候,表示新取了2个数据点,可以进行一次参数估计if (k == 0) {estimate(paramEstimator, data, numForEstimate, bestVotes, curVotes, numVotesForBest, arr);return;}//continue to recursivly generate the choice of indexesint endIndex = n - k;for (int i = startIndex; i <= endIndex; i++) {arr[arrIndex] = i;computeAllChoices(paramEstimator, data, numForEstimate, bestVotes, curVotes, numVotesForBest,i + 1, n, k - 1, arrIndex + 1, arr);//递归调用 }} //进行参数估计,并根据情况更新当前最佳模型的函数,最佳模型的局内点信息存储在数组bestVotes中,而局内点的数目则是由numVotesForBest存储 //arr数组存储的是本轮两个样本点在data中的索引值 template<class T, class S> void Ransac<T, S>::estimate(ParameterEsitmator<T, S> *paramEstimator, std::vector<T> &data, int numForEstimate,short *bestVotes, short *curVotes, int &numVotesForBest, int *arr){std::vector<T *> exactEstimateData;std::vector<S> exactEstimateParameters;int numDataObjects;int numVotesForCur;//initalize with -1 so that the first computation will be set to bestint j;numDataObjects = data.size();memset(curVotes, '\0', numDataObjects * sizeof(short));//数组中的点全部初始化为局外点numVotesForCur = 0;for (j = 0; j<numForEstimate; j++)exactEstimateData.push_back(&(data[arr[j]]));// 取出两个数据的地址paramEstimator->estimate(exactEstimateData, exactEstimateParameters);//用取出的两点来拟合出一组参数for (j = 0; j<numDataObjects; j++) {//依次判断是否为局内点if (paramEstimator->agree(exactEstimateParameters, data[j])) {curVotes[j] = 1;numVotesForCur++;}}//如果当前模型inlier的数目大于目前最佳模型inlier的数目,则取代目前最佳模型,并更新信息if (numVotesForCur > numVotesForBest) {numVotesForBest = numVotesForCur;memcpy(bestVotes, curVotes, numDataObjects * sizeof(short));} }
RANSAC算法的优缺点
- 该算法最大的优点就是具有较强的鲁棒性,即使数据集中存在明显错误的数据时,也可以得到较好的模型参数。但是要求局外点的数目不能太多,虽然我没有做过具体的实验,一般而言,局外点所占比例不能超过50%。当然后来又出现了一些改进的RANSAC算法,比如2013年Anders Hast提出的:Optimal RANSAC算法。
- 同时,RANSAC算法的缺点也是显而易见的,在本文给出的示例中,N个数据点,每次估计需要K个数据点,那么如果要遍历所有的情况,需要进行N!(N−K)!K!N!(N−K)!K!次参数估计过程,十分耗费资源。实际中一般不会全部遍历,而是根据经验设置一个合理的迭代次数,这显然不能保证最终得到的是最佳参数。此外,还涉及到误差阈值的选取问题,增加了算法的复杂度。
四、参数
我们不得不根据特定的问题和数据集通过实验来确定参数t和d。然而参数k(迭代次数)可以从理论结果推断。当我们从估计模型参数时,用p表示一些迭代过程中从数据集内随机选取出的点均为局内点的概率;此时,结果模型很可能有用,因此p也表征了算法产生有用结果的概率。用w表示每次从数据集中选取一个局内点的概率,如下式所示:
w = 局内点的数目 / 数据集的数目
通常情况下,我们事先并不知道w的值,但是可以给出一些鲁棒的值。假设估计模型需要选定n个点,wn是所有n个点均为局内点的概率;1 − wn是n个点中至少有一个点为局外点的概率,此时表明我们从数据集中估计出了一个不好的模型。 (1 − wn)k表示算法永远都不会选择到n个点均为局内点的概率,它和1-p相同。因此,
1 − p = (1 − wn)k
我们对上式的两边取对数,得出
值得注意的是,这个结果假设n个点都是独立选择的;也就是说,某个点被选定之后,它可能会被后续的迭代过程重复选定到。这种方法通常都不合理,由此推导出的k值被看作是选取不重复点的上限。例如,要从上图中的数据集寻找适合的直线,RANSAC算法通常在每次迭代时选取2个点,计算通过这两点的直线maybe_model,要求这两点必须唯一。
为了得到更可信的参数,标准偏差或它的乘积可以被加到k上。k的标准偏差定义为:
五、优点与缺点
RANSAC的优点是它能鲁棒的估计模型参数。例如,它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限;如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型,概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。
六、应用
RANSAC算法经常用于计算机视觉,例如同时求解相关问题与估计立体摄像机的基础矩阵。
七、参考文献
- Martin A. Fischler and Robert C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography". Comm. of the ACM 24: 381–395. doi:10.1145/358669.358692.
- David A. Forsyth and Jean Ponce (2003). Computer Vision, a modern approach. Prentice Hall. ISBN 0-13-085198-1.
- Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge University Press.
- P.H.S. Torr and D.W. Murray (1997). "The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix". International Journal of Computer Vision 24: 271–300. doi:10.1023/A:1007927408552.
- Ondrej Chum (2005). "Two-View Geometry Estimation by Random Sample and Consensus". PhD Thesis. http://cmp.felk.cvut.cz/~chum/Teze/Chum-PhD.pdf
- Sunglok Choi, Taemin Kim, and Wonpil Yu (2009). "Performance Evaluation of RANSAC Family". In Proceedings of the British Machine Vision Conference (BMVC). http://www.bmva.org/bmvc/2009/Papers/Paper355/Paper355.pdf.
八、外部链接
- RANSAC Toolbox for MATLAB. A research (and didactic) oriented toolbox to explore the RANSAC algorithm in MATLAB. It is highly configurable and contains the routines to solve a few relevant estimation problems.
- Implementation in C++ as a generic template.
- RANSAC for Dummies A simple tutorial with many examples that uses the RANSAC Toolbox for MATLAB.
- 25 Years of RANSAC Workshop
1. 经典RANSAC
由Fischer和Bolles在1981年的文章[1]中首先提出,简要的说经典RANSAC的目标是不断尝试不同的目标空间参数,使得目标函数 C 最大化的过程。这个过程是随机(Random)、数据驱动(data-driven)的过程。通过反复的随机选择数据集的子空间来产生一个模型估计,然后利用估计出来的模型,使用数据集剩余的点进行测试,获得一个得分,最终返回一个得分最高的模型估计作为整个数据集的模型。
1.1 目标函数
在经典的RANSAC流程中,目标函数C 可以被看作:在第k次迭代过程中,在当前变换参数作用下,数据集
中满足变换参数的点的个数,也就是在当前变换条件下类内点的个数,而RANSAC就是最大化 C 的的过程。而判断当前某个点是否为类内需要一个阈值t。
1.2 子集大小
1.3 循环终止条件
按照参考文献[1]中的说明,在置信度为的条件下,在循环过程中,至少有一次采样,使得采样出的m 个点均为类内点,这样才能保证在循环的过程中,至少有一次采样能取得目标函数的最大值。因此,采样次数k应该满足以下条件:
这里除了置信度外,m 为子集大小,ε 为类内点在
中的比例,其中置信度一般设置为[0.95, 0.99]的范围内。然而在一般情况下,ε 显然是未知的,因此 ε 可以取最坏条件下类内点的比例,或者在初始状态下设置为最坏条件下的比例,然后随着迭代次数,不断更新为当前最大的类内点比例。
另外一种循环终止条件可以将选取的子集看做为“全部是类内点”或“不全部是类内点”这两种结果的二项分布,而前者的概率为。对于 p 足够小的情况下,可以将其看作为一种泊松分布,因此,在 k 次循环中,有 n个“子集全部是类内点”的概率可以表达为:
λ 表示在 k 次循环中,“子集全都是类内点”的选取次数的期望。例如在RANSAC中,我们希望在这k次循环中所选子集“没有一个全是类内点”的概率小于某个置信度,即:,以置信度为95%为例,λ约等于3,表示在95%置信度下,在 k 次循环中,平局可以选到3次“好”的子集。
1.4 判断阈值的选取
α为置信概率,若 α=0.95,那么一个真实的类内点被误分类为类外点的概率为5%。
经典RANSAC算法的流程如下图所示:
2. Universal-RANSAC
经典RANSAC有以下三个主要的局限性:
(1) 效率:经典方法效率与子集大小、类内点比例以及数据集大小有关,因此在某些场景下效率较低。
(2) 精度:经典方法计算参数时选取最小子集是从效率的角度考虑,往往得到的是非最佳参数,在应用产参数 之前还需要再经过细化处理。
(3) 退化:经典方法的目标函数求取最大化的过程基于一个假设:“选取的最小子集中如果有类外点,那么在这种情况下估计的参数获得的目标函数(数据集中点的个数)往往较少“但这种情况在退化发生时有可能是不对的。
针对经典方法的这几项局限性,有很多改进,在这里提出了一种全局RANSAC(Universal-RANSAC)的结构图,每一种改进方法都可以看做是这种USAC的特例,如下图所示。
2.1 预滤波(Stage 0)
输入数据集,
含有 N 个点,在这一步中,SCRNMSAC[3],用一个一致性滤波器对初始的数据集进行滤波减少数量,然后将数据根据梯度排序。
2.2 最小子集采样(Stage 1)
对进行采样时,经典算法采用完全随机的方式,这种方式的前提是我们对数据的情况完全不知道,在实际应用中,很多情况对数据的先验知识是了解的,这对减少采样次数,尤其是类内点比例较低的数据集,有很大帮助,以下是几种在最小集采样当中对经典算法进行改进的方法。
Stage 1.a 采样
2.2.1 NAPSAC[4]
N-Adjacent points sample consensus(NAPSAC)算法认为:”数据集中,一个类内点与数据集中其他类内点的距离比类外点要近。”在一个n维空间中,假定:将数据集的n维空间看做一个超球面,随着半径的减少,类外点减少的速度比类内点要快(类外点距离球心更远)。这种算法可以描述为:
a. 中随机选取一个点 x ,设定一个半径 r,以 x 为中心 r 为半径建立超球面;
b. 超球面内包裹的点少于最小数据集的个数?返回 a,否则c
c. 均匀的从球体内取点,直至满足最小集中的个数。
这种方法对高维、类内点比例低的数据集效果明显,但是容易产生退化,且对于距离都很近的数据集效果差。
2.2.2 PROSAC[5]
2.2.3 GroupSAC[6]
与NAPSAC类似,GroupSAC认为类内点更加的“相似”,根据某种相似性将数据集中的点分组。以图像匹配为例,分组可以基于光流聚类(optical flow-based clustering)、图像分割等,然后按照PROSAC思想,采样可以从最大的聚类开始,因为这里应该有更高的类内点比例。但是这种方法首先要保证有一种先验知识可以用于分类,还有就是要保证分类算法的有效性和实时性。
Stage 1.b 采样验证
2.3 根据最小集产生模型(参数计算)(Stage 2)
Stage 2.a 模型计算
在这一步骤根据上一步选取的最小集计算参数,获得模型。
Stage 2.b 模型验证
还是利用先验知识,比如点集与圆形匹配,验证时候没必要将数据集中所有的点进行验证,而只是在得到模型(圆)的一个半径范围左右验证即可。
2.4 验证参数(Stage 3)
传统的方法在得到最小集产生的参数后计算全部集合中满足参数点的个数(目标函数),在此,加两步验证,分为两点:第一,验证当前的模型是否可能获得最大的目标函数。第二,当前模型是非退化的。
Stage 3.a 可能性验证
2.4.1 T(d,d)测试[5]
选取远小于数据集综述的 d 个点作为测试,只有当这 d 个点全都为类内点时,再对剩余的点进行测试,否则抛弃当前的模型。具体选取办法见论文[5].
2.4.2 Bail-Out测试[7]
选取集合中的若干点进行测试,若类内点的比例显著低于当前最佳模型类内点的比例,抛弃此模型。
2.4.3 SPRT测试[8,9]
挨个点测试,表示随机选取一个点符合当前模型的概率(good),
为“bad”的概率。根据以下公式,当阈值λ超过某阈值的时候抛弃当前模型。
2.4.4 Preemptive测试[10]
ARRSAC算法[11],首先产生多个模型,而不是产生一个后即对其评价,然后根据选取的一部分子集对所产生的模型按照目标函数得分排序,选取前若干个,做若干轮类似排序,选取最佳模型。
Stage 3.b 退化验证
数据退化的意思是无法提供足够的限制条件产生唯一解。传统RANSAC即没有这种安全的保障。
2.5 模型细化(Stage 4)
含有噪声的数据集有两个重要特点:1,即使子集中全都是类内点,产生的模型也并不一定适用于数据集中所有的类内点,这个现象增加了迭代的次数;2,最终收敛的RANSAC结果可能受到噪声未完全清理的影响,并不是全局最优的结果。
第一个影响往往被忽略,因为虽然增加了迭代次数,但是仍然返回的是一个准确的模型。而第二种影响就要增加一种模型细化的后处理。
2.5.1 局部最优化[12]
Lo-RANSAC,局部最优RANSAC。在迭代过程中,出现当前最优解,进行Lo-RANSAC。一种方法是从返回结果的类内点中再进行采样计算模型,设置一个固定的迭代次数(10-20次)然后选取最优的局部结果作为改进的结果,另一种方法是设置一个优化参数K(2~3),选取结果中判断阈值(t)小于等于Kt 的结果作为优化结果,K 减小,直至减小至 t 终止。
2.5.1 错误传播法[13]
思想与Lo-RANSAC一致,但是更为直接,因为初始的RANSAC结果产生自含有噪声的数据集,因此这个错误“传播”到了最终的模型,协方差可以看做是估计两个数据集关系是一种不确定的信息(而如上所述,判断阈值的计算是固定的)。具体方法参见文献[13]。
2.6 最终方案--USAC-1.0
最终选取的结果如下图所示:
stage1: 最小集采样方法采用2.2.2节中的PROSAC。
stage3: 模型(参数)验证采用2.4.3的SPRT测试。
stage4: 产生最终模型,采用2.5.1介绍的Lo-RANSAC。
论文翻译自:文献[0]。
----------------------------参考文献---------------------------
[0] Raguram R, Chum O, Pollefeys M, et al. USAC: A Universal Framework for Random Sample Consensus[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2013, 35(8):2022-2038.
[1] M.A. Fischler and R.C. Bolles, “Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography,” Comm. ACM, vol. 24, no. 6, pp. 381- 395,1981.
[2] R.I. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision. Cambridge Univ. Press, 2000
[3] T. Sattler, B. Leibe, and L. Kobbelt, “SCRAMSAC: Improving RANSAC’s Efficiency with a Spatial Consistency Filter,” Proc. 12th IEEE Int’l Conf. Computer Vision, 2009.
[4] D.R. Myatt, P.H.S. Torr, S.J. Nasuto, J.M. Bishop, and R. Craddock,“NAPSAC: High Noise, High Dimensional Robust Estimation,”Proc. British Machine Vision Conf., pp. 458-467, 2002.
[5] O. Chum and J. Matas, “Matching with PROSAC—Progressive Sample Consensus,” Proc. IEEE Conf. Computer Vision and Pattern Recognition, 2005.
[6] K. Ni, H. Jin, and F. Dellaert, “GroupSAC: Efficient Consensus in the Presence of Groupings,” Proc. 12th IEEE Int’l Conf. Computer Vision, Oct. 2009.
[7] D. Capel, “An Effective Bail-Out Test for RANSAC Consensus Scoring,” Proc. British Machine Vision Conf., 2005.
[8] O. Chum and J. Matas, “Optimal Randomized RANSAC,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 30, no. 8,pp. 1472-1482, Aug. 2008.
[9] J. Matas and O. Chum, “Randomized RANSAC with Sequential Probability Ratio Test,” Proc. 10th IEEE Int’l Conf. Computer Vision,vol. 2, pp. 1727-1732, Oct. 2005.
[10] D. Niste´r, “Preemptive RANSAC for Live Structure and Motion Estimation,” Proc. Ninth IEEE Int’l Conf. Computer Vision, 2003.
[11] R. Raguram, J.-M. Frahm, and M. Pollefeys, “A Comparative Analysis of RANSAC Techniques Leading to Adaptive Real-Time Random Sample Consensus,” Proc. European Conf. Computer Vision, pp. 500- 513. 2008,
[12] O. Chum, J. Matas, and J. Kittler, “Locally Optimized RANSAC,”Proc. DAGM-Symp. Pattern Recognition, pp. 236-243, 2003.
[13] R. Raguram, J.-M Frahm, and M. Pollefeys, “Exploiting Uncertainty in Random Sample Consensus,” Proc. 12th IEEE Int’l Conf. Computer Vision, Oct. 2009.
相关文章:

【ACM】树 小结
树是一种表达层级结构的数据结构,也是实现高效算法与数据结构的基础。 学习之前的基础:数组,循环处理,结构体,递归函数。 树:由结点(node)和连接结点的边(edge…

【cocos2d-js官方文档】九、cc.loader
概述 原来的cc.Loader被改造为一个单例cc.loader,采用了插件机制设计,让loader做更纯粹的事。 各种资源类型的loader可以在外部注册进来,而不是直接将所有的代码杂揉在cc.Loader中,更好的方便管理以及用户自定义loader的创建。 cc…

更换VC后DDC提示证书不可用
问题描述:客户环境由Windows VC更换成Linux VC后,DDC提示证书不可用问题原因:因为VC更换后,存储在DDC数据库HostingUnitServiceSchema.HypervisorConnectionSSLThumbprint表中证书指纹信息和新得VC证书指纹信息不匹配。解决方法&a…

尺度空间理论与图像金字塔
我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性。也就是说使用卷积就是为了提取显著特征,减少特征维数,减少计算量。 在对图像进行卷积操作后的只管现象:图像变得模糊了,可是我们依然能够分辨出是什么&#x…

【ACM】 multiset 的 一些应用
一、The kth great number 题目链接:https://vjudge.net/problem/HDU-4006 用set写超时 (在VJ里,用C显示Compilation Error,选择G,则是TLE) #include <iostream> #include <set> #include &…

apache2.2 做后端,增加真实ip到日志中
apache2.2使用mod_remoteip模块 一.安装 wget https://github.com/ttkzw/mod_remoteip-httpd22/raw/master/mod_remoteip.c/usr/local/apache/bin/apxs -i -c -n mod_remoteip.so mod_remoteip.c 二.添加Apache配置vi /usr/local/apache/conf/httpd.confInclude conf/extra/htt…

高可用方案系统架构
2019独角兽企业重金招聘Python工程师标准>>> 高可用方案 系统架构 转载于:https://my.oschina.net/qiongtaoli/blog/3007587

OpenCV3.2.0+VS2017在window10开发环境配置记录
本机环境:win10 64位 OpenCV3.2.0 Visual Studio 2017 最后结果,亲测可用OpenCV官方下载地址: http://opencv.org/releases.html#本人选择opencv3.2.0基于Windows平台。读者根据自己需要选择合适版本及平台下载。 选择window版本的opencv下载…
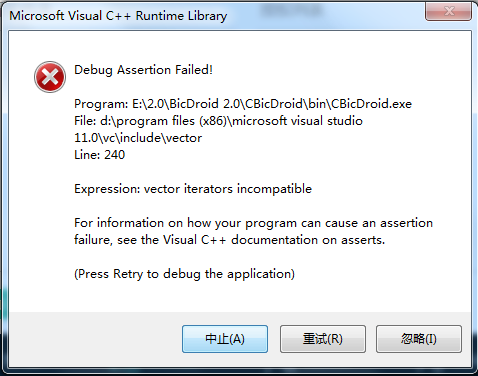
C++vector迭代器失效的问题
转载:http://blog.csdn.net/olanmomo/article/details/38420907 转载:http://blog.csdn.net/stpeace/article/details/46507451 转载:http://www.cnblogs.com/xkfz007/articles/2509433.html 转载:http://www.cnblogs.com/BeyondAnyTime/archive/2012/08/13/2636375.html 有这样…

【HDU】1251统计难题 (字典树:二维数组,结构体数组,链表,map)
使用二维数组或者结构体数组都可以,但是在计数的时候有一点点小区别 一、结构体数组 #include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <string> typedef long long ll; using namespace…
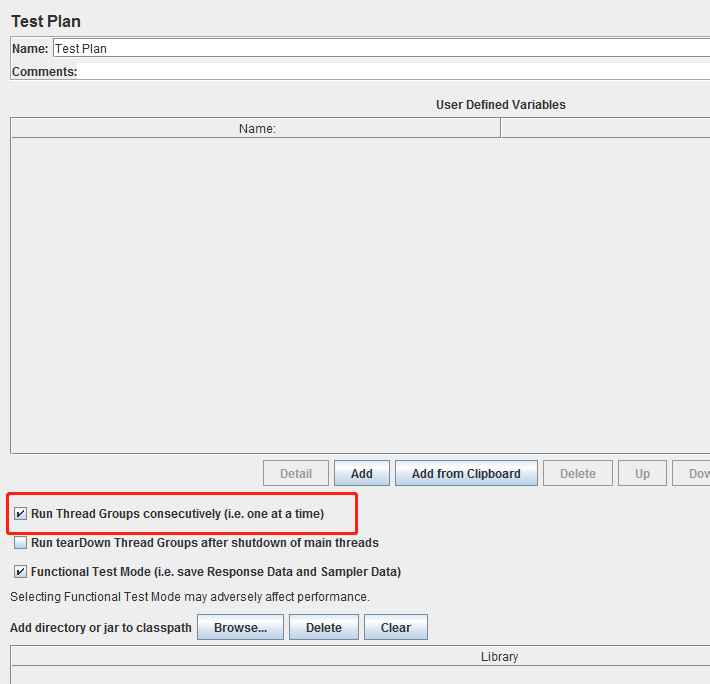
Jmeter干货 不常用却极其有用的几个地方
1. Jmeter测试计划下Run Thread Groups consecutively 表示序列化执行测试计划下所有线程组中的各个请求 如下图配置,新建的测试计划中,不默认勾选此项, 而享用Jmeter做接口自动化测试的同学们,会发现一个问题是,可能多…

图像滤波总结(面试经验总结)
目录 图像平滑处理,6种滤波总结的综合示例 【盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波导向滤波】 1-图像滤波 2-代码演示 3-显示结果 4-程序说明 5 角点检测(Harris,Fast,surf) 图像平滑处理,6种滤波总结的综合示…

【小贴士】DEV 多行注释
多行注释 Ctrl / 取消多行注释 Ctrl ,

JSP+Servlet基础一
2019独角兽企业重金招聘Python工程师标准>>> JSP中的指令: 格式:<%指令的名称(page,taglib,include...) 属性属性值%> 指令中的page:用于整个页面,定义与页面相关的属性。page属性一共有13个。 1、常…

Chameleon跨端框架——壹个理想主义团队的开源作品
文章较长,信息量很大,请耐心阅读,必然有收获。下面正文开始~背景解决方案原理久经考验生产应用举例易用性好多态协议学习成本低渐进式接入业内对比后期规划理想主义历经近20个月打磨,滴滴跨端方案chameleon终于开源了github.com/d…

尺度空间理论与图像金字塔(二)
SIFT简介 整理一下方便阅读,作者写的东西摘自论文,在此感谢xiaowei等的贡献 DoG尺度空间构造(Scale-space extrema detection)http://blog.csdn.net/xiaowei_cqu/article/details/8067881关键点搜索与定位(Keypoint l…

仿桌面通知pnotify插件
在做网站的时候,alert弹出框是非常常见的情形。但是,有些情况下,弹框对用户来说是并不友好的。调研了几个其他的提示插件了,发现pnotify比较好用,可配置性也高。 使用示例: <!DOCTYPE html> <html…

【HDU】1305 Immediate Decodability(字典树:结构体数组,二维数组,链表/指针)
一、用的二维数组 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int maxn 100; int tr[maxn][2]; int mk[maxn]; int tot;void insert(string s) {int u 0;for(int i0;i<s.length();i){int x s[i]-0;if(tr…

Hyperledger Grid:一个用于分布式供应链解决方案的框架
Hyperledger在最近的一篇博文中发布了一个名为Hyperledger Grid的新项目。Grid是一个用于集成分布式账本技术(DLT)解决方案与供应链行业企业业务系统的框架。该项目提供了一个参考架构、通用数据模型和智能合约,所有这些都是基于开放标准和行…

尺度不变特征变换匹配算法详解
尺度不变特征变换匹配算法详解Scale Invariant Feature Transform(SIFT)Just For Fun对于初学者,从David G.Lowe的论文到实现,有许多鸿沟,本文帮你跨越。1、SIFT综述 尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视…

【POJ】2503 Babelfish(字典树,map,指针)
一、map 输入时候的格式有点难想,还有一种想法是用gets读取,然后用sscanf分开,分别存到两个数组中去,再加入map中,但是这一种方法目前还没有实现。。 #include <iostream> #include <cstring> #include …

ndk-build: CreateProcess error=193
为什么80%的码农都做不了架构师?>>> 问题:ndk-build": CreateProcess error193 解决:该问题表明,调用了非windows程序,在build.xml中将ndk-build修改为ndk-build.cmd即可ant编译 转载于:https://my.o…

AI芯片初创公司单纯卖芯片还是捆绑算法的商业模式更好?...
雷锋网在《资本寒冬,这样的AI芯片公司2019年危矣》一文中已经提到,2019年的资本寒冬以及整个半导体行业的低迷,将会让那些没有技术独特性以及缺乏商业落地能力,且现金流控制不好的AI芯片公司面临巨大的挑战,甚至大概率…
VS2017配置OpenCV3.2+contrib3.2
VS2017配置OpenCV3.2contrib3.2前言opecv3.2opencv_contrib3.2模块都编译配置了在配置contrib之前,尝试直接配置OpeCV3.2-vc14,发现可以正常使用,也就是说官方包虽然只有vc14,但vs2017(vc15)也支持的很好。操作环境:WIN10 64bit &…
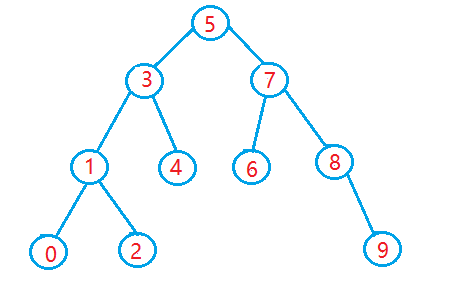
【ACM】二叉搜索树(Binary Search Tree /BS Tree) 小结
动态管理集合的数据结构——二叉搜索树 搜索树是一种可以进行插入,搜索,删除等操作的数据结构,可以用字典或者优先队列。 二叉排序树又称为二叉查找树,他或者为空树,或者是满足如下性质的二叉树。 (1&…

android安卓动态设置控件宽高
LayoutParams layoutParamsp_w_picpathView.getLayoutParams();layoutParams.width100;layoutParams.height200;p_w_picpathView.setLayoutParams(layoutParams);转载于:https://blog.51cto.com/11020803/1860242

《深入java虚拟机》读书笔记类加载
概述 类加载机制是指虚拟机将描述类的数据从Class文件中加载到内存,并进行数据验证、解析、初始化等过程,最后形成可以直接被虚拟机使用的java类型。在java语言中类的加载、链接、初始化等过程并不是在编译时期完成,而是在运行时期才进行的&a…

SLAM之特征匹配(一)————RANSAC-------OpenCV中findFundamentalMat函数使用的模型
目录 1.RANSAC原理 2. RANSAC算法步骤: 3. RANSAC源码解析 step one niters最初的值为2000,这就是初始时的RANSAC算法的循环次数,getSubset()函数是从一组对应的序列中随机的选出4组(因为要想计算出一…

I hope so 2016-Oct-10
2019独角兽企业重金招聘Python工程师标准>>> <I hope so> - A joke A: Do you think your son will forget all he learned at college? B: I hopse so. He certainly cant make a living by kissing girls! 转载于:https://my.oschina.net/u/553266/blog/75…

【Codeforces】158B-Taxi(贪心,怎么贪咧)
贪心 emmmm http://codeforces.com/contest/158/problem/B 题目大意:有四种旅客,四人一组,三人一组,两人一组,一人一组,一辆出租车最多可以坐四个人,并且一组里的人必须坐一辆车,…