【ACM】树 小结
树是一种表达层级结构的数据结构,也是实现高效算法与数据结构的基础。
学习之前的基础:数组,循环处理,结构体,递归函数。
树:由结点(node)和连接结点的边(edge)构成。


一、树的相关基本概念:
双亲(父母/前件),子女(孩子/后件),双亲和子女的关系是相对而言的。
兄弟:若几个结点的双亲为同一个结点,则这些结点互称为兄弟。
祖先:将从树根到某一结点K的路径中,K前所经过的所有结点称为K的祖先。
子孙:以某结点K为根的子树中的任意一个结点都称为K的子孙。
结点的度:某一结点拥有的子女的个数。
树的度:树中所有结点的度的最大值。
叶子节点(终端节点):度为0的结点。
分支节点(非终端节点):度不为0的结点。
结点的层次:(有两种不同的说法,有的说根结点所在层次是0,有的说根结点所在层次是1)
树的深度(高度):树中结点的最大层次数。
在一棵树中,除了根节点外,其他任何结点有且仅有一个双亲,有0个或多个子女,他的子女恰巧为其子树的根结点。
二叉树:二叉树是一个由结点构成的有限集合,这个集合或者为空,或者由一个根结点及两棵互不相交的分别称作这个根结点的左子树和右子树的二叉树组成。
有序树:若树中任意结点的子树均看成是从左到右有次序的,不能随意交换,则称该树是有序树。
------------------------------------------------------------------------------------------
二叉树不是一般树形结构的特殊形式,它们是两种不同的数据结构
区别:
1、二叉树中每一个非空结点最多只有两个子女,而一般的树形结构中每个非空结点可以有0到多个结点。
2、二叉树中结点的子树要区分左子树和右子树,即使在结点只有一颗子树的情况下,也要明确指出是左子树还是右子树。
------------------------------------------------------------------------------------------
现学现用
1、Rooted Trees(有根树的表达)
https://vjudge.net/problem/Aizu-ALDS1_7_A
这题是对一棵树结点的相关信息进行输出,输入数据完成,则是一棵确定的树
关键是用什么方法存储一个结点的信息(结点序号,双亲结点的序号,深度,结点类型,所有子女序号)
这里使用的是:左子右兄弟表示法
该方法包含以下信息:1、结点的父结点。2、结点最左侧子结点。3、结点右侧紧邻的兄弟结点。
//左子右兄弟表示法
typedef struct
{int parent;int left;int right;
}Node;#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int maxn = 100000+10;//左子右兄弟表示法
typedef struct
{int parent;int left;int right;
}Node;Node T[maxn];int n;int getdepth(int u)
{int d=0;while(T[u].parent!=-1){u=T[u].parent;d++;}return d;
}void print(int u)
{int i,c;cout << "node "<<u<<": parent = "<<T[u].parent<<", depth = "<<getdepth(u)<<", ";if(T[u].parent==-1)cout << "root, ";else if (T[u].left==-1)cout << "leaf, ";else cout <<"internal node, ";cout <<"[";for(i=0,c=T[u].left;c!=-1;i++,c=T[c].right){if(i) cout<<", ";cout << c;}cout << "]"<<endl;
}int main ()
{int i,j,id,k,c,l;scanf("%d",&n);for(i=0;i<n;i++){T[i].left=-1;T[i].parent=-1;T[i].right=-1;}for(i=0;i<n;i++){cin >> id >> k;for(j=0;j<k;j++){cin >> c;if(j==0) T[id].left=c;elseT[l].right=c;l=c;T[c].parent=id;}}for(i=0;i<n;i++)print(i);return 0;
}2、Binary Tree(二叉树的表达)
这个题是对二叉树的相关信息进行输出,结点的双亲的序号,它的兄弟结点,该结点的度,该结点的深度(层次数),该结点高(该结点往下,到叶子节点的最长路径),该结点的类型
与上一题相比,该结点的度是小于等于2的,及最多有两个子女,比上一题的树可能有0到多个子女方便处理一些。
#include <iostream>
using namespace std;
typedef struct
{int p,l,r;
}node;node T[100000+5];int getdepth(int u)
{//到根结点的距离 int d= 0;while(T[u].p!=-1){u=T[u].p;d++;} return d;
}int sibling(int u)
{if(T[u].p==-1)return -1;if(T[T[u].p].l!=u && T[T[u].p].l!=-1)return T[T[u].p].l;if(T[T[u].p].r!=u && T[T[u].p].r!=-1)return T[T[u].p].r;return -1;
}int getdegree(int u)
{int d=0;if(T[u].l!=-1)d++;if(T[u].r!=-1)d++;return d;
}int getheight(int u)
{int a=0,b=0;if(T[u].l!=-1)a = getheight(T[u].l)+1;if(T[u].r!=-1)b = getheight(T[u].r)+1;return (a>b)?a:b;
}void print(int u)
{cout << "node "<<u;cout << ": parent = "<<T[u].p;cout << ", sibling = "<<sibling(u);cout << ", degree = "<<getdegree(u); cout << ", depth = "<<getdepth(u);cout << ", height = "<<getheight(u);if(T[u].p==-1)cout <<", root\n";else if(T[u].l==-1 && T[u].r==-1)cout << ", leaf\n";elsecout <<", internal node\n";
}int main ()
{int i,N;cin >>N;for(i=0;i<N;i++){T[i].p=-1;T[i].l=-1;T[i].r=-1;}int id,l,r;for(i=0;i<N;i++){cin >> id>> l >> r;T[id].l=l;T[id].r=r;if(l!=-1)T[l].p=id;if(r!=-1)T[r].p=id;}for(int i=0;i<N;i++)print(i); return 0;
}
二、树的遍历
树的常用遍历:
(1)树的前序遍历。首先访问根结点,再从左到右依次按前序遍历的方式访问根结点的每一棵子树。
(2)树的后序遍历。首先从左到右依次按后序遍历的方式访问根结点的每一棵子树,然后再访问根结点。
(3)树的层次遍历。首先访问第一层上的根结点,然后从左到右依次访问第二层上的所有结点,再以同样的方式访问第三层上所有结点......最后访问树中最低一层的所有结点。
前序遍历:a b c e f h i g d
后序遍历:b e h i f g c d a
层次遍历:a b c d e f g h i
二叉树的遍历
是指按照一定的顺序对二叉树中的每一个结点均访问一次,且仅访问一次。
按照根结点访问位置的不同,通常把二叉树的遍历分为3种:前序遍历,中序遍历,后序遍历
(1)前序遍历:(根,左,右)
首先访问根结点;
然后按照前序遍历的方式访问根结点的左子树;
再按照前序遍历的方式访问根结点的右子树。
(2)中序遍历(左,根,右)
(3)后序遍历(左,右,根)
前序遍历:a b d e f g c
中序遍历:d e b g f a c
后序遍历:e d g f b c a
现学现用:
typedef struct
{int parent;int left;int right;
}Node;1、Tree Walk
https://vjudge.net/problem/Aizu-ALDS1_7_C
输出三种遍历结果,注意输出格式
采用的是递归地遍历二叉树
#include <iostream>
using namespace std;const int maxn = 50;typedef struct
{int parent;int left;int right;
}Node;Node T[maxn];
int n;void preorder(int u)
{if(u==-1)return ;cout << " "<<u;preorder(T[u].left);preorder(T[u].right);
}void inorder(int u)
{if(u==-1)return ;inorder(T[u].left);cout << " "<<u;inorder(T[u].right);
}void postorder(int u)
{if(u==-1)return ;postorder(T[u].left);postorder(T[u].right);cout << " "<<u;
}int main ()
{int i;cin >> n;for(i=0;i<n;i++){T[i].parent=-1;T[i].left=-1;T[i].right=-1;}int id,rchild,lchild;for(i=0;i<n;i++){cin >> id >> lchild >> rchild;T[id].left=lchild;T[id].right=rchild;if(rchild!=-1)T[rchild].parent=id;if(lchild!=-1)T[lchild].parent=id;}int root;for(i=0;i<n;i++){if(T[i].parent==-1){root=i;}}cout << "Preorder\n" ;preorder(root);cout <<"\nInorder\n";inorder(root);cout << "\nPostorder\n";postorder(root);cout << endl;return 0;
}
下面是非递归地遍历二叉树
需要用到栈stack
前序遍历(根,左,右)
对于一棵二叉树t,如果t非空,访问完t的根结点值后,就应该进入t的左子树,但此时必须将t保存起来,以便访问完其左子树后,进入其右子树访问,即应该在t处设置一个回溯点,并将该回溯点进栈保存。
void preorder(int u)
{stack<int> s;while((u!=-1) || s.empty()!=1){if(u!=-1){cout << " " << u;s.push(u);u=T[u].left;}else{u=s.top();s.pop();u=T[u].right;}}
}中序遍历:(左,根,右)
对于一棵树t,如果t非空,首先应将进入t的左子树访问,此时由于t的根结点即右子树尚未访问,因此必须将t保存起来放入栈中,以便访问完其左子树后,从栈中取出t,进行其根结点及右子树的访问。
void inorder(int u)
{stack<int> s;while((u!=-1)||(s.empty()!=1)){if(u!=-1){s.push(u);u=T[u].left;}else{u=s.top();cout << " "<<u;s.pop();u=T[u].right;}}
}后序遍历(左,右,根)
对于一棵树t,首先应该进入t的左子树访问,此时由于t的右子树及根结点尚未访问,因此必须将t保存起来放入栈中,以便访问完其左子树后,从栈种取出t,
void postorder(int u)
{stack<int> S,s;//s用来标记,S用来暂存数据while((u!=-1)||(S.empty()!=1)){if(u!=-1){S.push(u);s.push(0);u=T[u].left;}else{if(s.top()==1){s.pop();u=S.top();S.pop();cout << " "<<u;u=-1;}else{u=S.top();s.top()=1;u=T[u].right;}}}
}三、树遍历的应用——树的重建
分别输入二叉树的前序遍历和中序遍历,输出相应的后序遍历
分别输入二叉树的中序遍历和后序遍历,输出相应的前序遍历
无法通过前序遍历和后序遍历求的中序遍历:前序和后序在本质上都是将父节点与子结点进行分离,但并没有指明左子树和右子树的能力,因此得到这两个序列只能明确父子关系,而不能确定一个二叉树。
现学现用
1、Binary Tree Traversals(知道前序,中序求后序)
前序遍历 (根左右):1 2 4 7 3 5 8 9 6
中序遍历(左根右):4 7 2 1 8 5 9 3 6
https://vjudge.net/problem/HDU-1710
核心代码!!!!(递归的思想)
void fun(int l,int r)
{//distance函数返回的是两迭代器之间的距离if(l>=r) return ;int root=pre[pos++];int m = distance(in.begin(),find(in.begin(),in.end(),root));fun(l,m);fun(m+1,r);post.push_back(root);
}测试样例:
5
1 2 3 4 5(前序遍历)
3 2 4 1 5(中序遍历)
设前序遍历的当前结点c,c在中序遍历中的位置是m,m的左侧就是c的左子树,右侧就是c的右子树,然后同理递归。
例如
当前的结点为1,其在中序遍历中的位置是 3 2 4 [1] 5,那么当前树的根就是1,左右子树就是 3 2 4 和 5。接下来在3 2 4 组成的树中,前序遍历的下一个结点是2是根,3 [2] 4,3和4是两个子树。以此类推...
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;vector<int> pre,in,post;
int pos,n;void fun(int l,int r)
{//distance函数返回的是两迭代器之间的距离if(l>=r) return ;int root=pre[pos++];int m = distance(in.begin(),find(in.begin(),in.end(),root));fun(l,m);fun(m+1,r);post.push_back(root);
}void solve()
{int i;pos=0;fun(0,pre.size());for(i=0;i<n;i++){if(i!=(n-1))printf("%d ",post[i]);else printf("%d\n",post[i]);}
}int main ()
{int i,x;while(scanf("%d",&n)!=EOF){pre.clear();in.clear();post.clear();for(i=0;i<n;i++){cin >> x;pre.push_back(x);}for(i=0;i<n;i++){cin >> x;in.push_back(x);}solve();}return 0;
}2、Tree Recovery(知道前序、中序求后序)
https://vjudge.net/problem/POJ-2255
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;vector<char> pre,in,post;
int pos,n;void fun(int l,int r)
{if(l>=r)return ;char root = pre[pos++];int m = distance(in.begin(),find(in.begin(),in.end(),root));fun(l,m);fun(m+1,r);post.push_back(root);
}void solve()
{pos = 0;fun(0,pre.size());for(int i=0;i<pre.size();i++)cout << post[i];cout << endl;
}int main ()
{//直到前序,中序,求后序char s1[1000],s2[1000];int i;while(scanf("%s %s",s1,s2)!=EOF){i=0;pre.clear();in.clear();post.clear();while(s1[i]){pre.push_back(s1[i]);i++;}i=0;while(s2[i]){in.push_back(s2[i]);i++;}solve();}return 0;
}3、756-重建二叉树(知道后序和中序,求前序)
http://nyoj.top/problem/756
这个题目和之前的两个题目有一点不同,思想都是一样的,但是后序遍历是左右根,所以,需要不断地往前推,而且在往前推的过程中,先得到的是右子树上的根结点,再次是左子树上的,所以存入pre这个vector中的顺序是“右左根”,所以在输出的时候要倒序输出。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
vector<char> pre,in,post;
int pos,n;
char s1[1000],s2[1000];
void fun(int l,int r)
{if(l>=r)return ;char root = post[pos--];int m = distance(in.begin(),find(in.begin(),in.end(),root));fun(m+1,r);fun(l,m);pre.push_back(root);
}
void solve()
{pos = strlen(s1)-1;fun(0,in.size());for(int i=in.size()-1;i>=0;i--){cout << pre[i];}cout << endl;
}
int main ()
{//知道后序和中序遍历,求前序遍历int i;while(scanf("%s %s",s1,s2)!=EOF){i=0;pre.clear();in.clear();post.clear();while(s1[i]){post.push_back(s1[i]);i++;}i=0;while(s2[i]){in.push_back(s2[i]);i++;}solve();}return 0;
}相关文章:

【cocos2d-js官方文档】九、cc.loader
概述 原来的cc.Loader被改造为一个单例cc.loader,采用了插件机制设计,让loader做更纯粹的事。 各种资源类型的loader可以在外部注册进来,而不是直接将所有的代码杂揉在cc.Loader中,更好的方便管理以及用户自定义loader的创建。 cc…

更换VC后DDC提示证书不可用
问题描述:客户环境由Windows VC更换成Linux VC后,DDC提示证书不可用问题原因:因为VC更换后,存储在DDC数据库HostingUnitServiceSchema.HypervisorConnectionSSLThumbprint表中证书指纹信息和新得VC证书指纹信息不匹配。解决方法&a…

尺度空间理论与图像金字塔
我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性。也就是说使用卷积就是为了提取显著特征,减少特征维数,减少计算量。 在对图像进行卷积操作后的只管现象:图像变得模糊了,可是我们依然能够分辨出是什么&#x…

【ACM】 multiset 的 一些应用
一、The kth great number 题目链接:https://vjudge.net/problem/HDU-4006 用set写超时 (在VJ里,用C显示Compilation Error,选择G,则是TLE) #include <iostream> #include <set> #include &…

apache2.2 做后端,增加真实ip到日志中
apache2.2使用mod_remoteip模块 一.安装 wget https://github.com/ttkzw/mod_remoteip-httpd22/raw/master/mod_remoteip.c/usr/local/apache/bin/apxs -i -c -n mod_remoteip.so mod_remoteip.c 二.添加Apache配置vi /usr/local/apache/conf/httpd.confInclude conf/extra/htt…

高可用方案系统架构
2019独角兽企业重金招聘Python工程师标准>>> 高可用方案 系统架构 转载于:https://my.oschina.net/qiongtaoli/blog/3007587

OpenCV3.2.0+VS2017在window10开发环境配置记录
本机环境:win10 64位 OpenCV3.2.0 Visual Studio 2017 最后结果,亲测可用OpenCV官方下载地址: http://opencv.org/releases.html#本人选择opencv3.2.0基于Windows平台。读者根据自己需要选择合适版本及平台下载。 选择window版本的opencv下载…
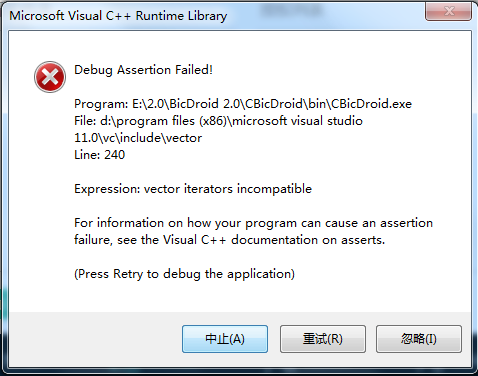
C++vector迭代器失效的问题
转载:http://blog.csdn.net/olanmomo/article/details/38420907 转载:http://blog.csdn.net/stpeace/article/details/46507451 转载:http://www.cnblogs.com/xkfz007/articles/2509433.html 转载:http://www.cnblogs.com/BeyondAnyTime/archive/2012/08/13/2636375.html 有这样…

【HDU】1251统计难题 (字典树:二维数组,结构体数组,链表,map)
使用二维数组或者结构体数组都可以,但是在计数的时候有一点点小区别 一、结构体数组 #include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <string> typedef long long ll; using namespace…
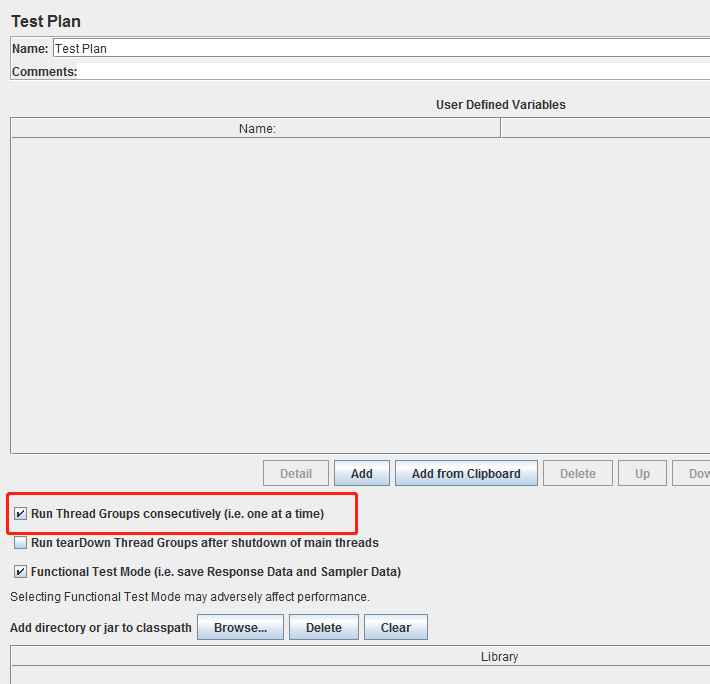
Jmeter干货 不常用却极其有用的几个地方
1. Jmeter测试计划下Run Thread Groups consecutively 表示序列化执行测试计划下所有线程组中的各个请求 如下图配置,新建的测试计划中,不默认勾选此项, 而享用Jmeter做接口自动化测试的同学们,会发现一个问题是,可能多…

图像滤波总结(面试经验总结)
目录 图像平滑处理,6种滤波总结的综合示例 【盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波导向滤波】 1-图像滤波 2-代码演示 3-显示结果 4-程序说明 5 角点检测(Harris,Fast,surf) 图像平滑处理,6种滤波总结的综合示…

【小贴士】DEV 多行注释
多行注释 Ctrl / 取消多行注释 Ctrl ,

JSP+Servlet基础一
2019独角兽企业重金招聘Python工程师标准>>> JSP中的指令: 格式:<%指令的名称(page,taglib,include...) 属性属性值%> 指令中的page:用于整个页面,定义与页面相关的属性。page属性一共有13个。 1、常…

Chameleon跨端框架——壹个理想主义团队的开源作品
文章较长,信息量很大,请耐心阅读,必然有收获。下面正文开始~背景解决方案原理久经考验生产应用举例易用性好多态协议学习成本低渐进式接入业内对比后期规划理想主义历经近20个月打磨,滴滴跨端方案chameleon终于开源了github.com/d…

尺度空间理论与图像金字塔(二)
SIFT简介 整理一下方便阅读,作者写的东西摘自论文,在此感谢xiaowei等的贡献 DoG尺度空间构造(Scale-space extrema detection)http://blog.csdn.net/xiaowei_cqu/article/details/8067881关键点搜索与定位(Keypoint l…

仿桌面通知pnotify插件
在做网站的时候,alert弹出框是非常常见的情形。但是,有些情况下,弹框对用户来说是并不友好的。调研了几个其他的提示插件了,发现pnotify比较好用,可配置性也高。 使用示例: <!DOCTYPE html> <html…

【HDU】1305 Immediate Decodability(字典树:结构体数组,二维数组,链表/指针)
一、用的二维数组 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int maxn 100; int tr[maxn][2]; int mk[maxn]; int tot;void insert(string s) {int u 0;for(int i0;i<s.length();i){int x s[i]-0;if(tr…

Hyperledger Grid:一个用于分布式供应链解决方案的框架
Hyperledger在最近的一篇博文中发布了一个名为Hyperledger Grid的新项目。Grid是一个用于集成分布式账本技术(DLT)解决方案与供应链行业企业业务系统的框架。该项目提供了一个参考架构、通用数据模型和智能合约,所有这些都是基于开放标准和行…

尺度不变特征变换匹配算法详解
尺度不变特征变换匹配算法详解Scale Invariant Feature Transform(SIFT)Just For Fun对于初学者,从David G.Lowe的论文到实现,有许多鸿沟,本文帮你跨越。1、SIFT综述 尺度不变特征转换(Scale-invariant feature transform或SIFT)是一种电脑视…

【POJ】2503 Babelfish(字典树,map,指针)
一、map 输入时候的格式有点难想,还有一种想法是用gets读取,然后用sscanf分开,分别存到两个数组中去,再加入map中,但是这一种方法目前还没有实现。。 #include <iostream> #include <cstring> #include …

ndk-build: CreateProcess error=193
为什么80%的码农都做不了架构师?>>> 问题:ndk-build": CreateProcess error193 解决:该问题表明,调用了非windows程序,在build.xml中将ndk-build修改为ndk-build.cmd即可ant编译 转载于:https://my.o…

AI芯片初创公司单纯卖芯片还是捆绑算法的商业模式更好?...
雷锋网在《资本寒冬,这样的AI芯片公司2019年危矣》一文中已经提到,2019年的资本寒冬以及整个半导体行业的低迷,将会让那些没有技术独特性以及缺乏商业落地能力,且现金流控制不好的AI芯片公司面临巨大的挑战,甚至大概率…
VS2017配置OpenCV3.2+contrib3.2
VS2017配置OpenCV3.2contrib3.2前言opecv3.2opencv_contrib3.2模块都编译配置了在配置contrib之前,尝试直接配置OpeCV3.2-vc14,发现可以正常使用,也就是说官方包虽然只有vc14,但vs2017(vc15)也支持的很好。操作环境:WIN10 64bit &…
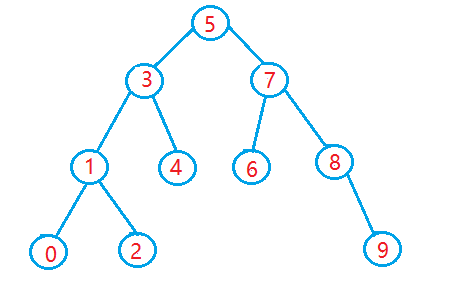
【ACM】二叉搜索树(Binary Search Tree /BS Tree) 小结
动态管理集合的数据结构——二叉搜索树 搜索树是一种可以进行插入,搜索,删除等操作的数据结构,可以用字典或者优先队列。 二叉排序树又称为二叉查找树,他或者为空树,或者是满足如下性质的二叉树。 (1&…

android安卓动态设置控件宽高
LayoutParams layoutParamsp_w_picpathView.getLayoutParams();layoutParams.width100;layoutParams.height200;p_w_picpathView.setLayoutParams(layoutParams);转载于:https://blog.51cto.com/11020803/1860242

《深入java虚拟机》读书笔记类加载
概述 类加载机制是指虚拟机将描述类的数据从Class文件中加载到内存,并进行数据验证、解析、初始化等过程,最后形成可以直接被虚拟机使用的java类型。在java语言中类的加载、链接、初始化等过程并不是在编译时期完成,而是在运行时期才进行的&a…

SLAM之特征匹配(一)————RANSAC-------OpenCV中findFundamentalMat函数使用的模型
目录 1.RANSAC原理 2. RANSAC算法步骤: 3. RANSAC源码解析 step one niters最初的值为2000,这就是初始时的RANSAC算法的循环次数,getSubset()函数是从一组对应的序列中随机的选出4组(因为要想计算出一…

I hope so 2016-Oct-10
2019独角兽企业重金招聘Python工程师标准>>> <I hope so> - A joke A: Do you think your son will forget all he learned at college? B: I hopse so. He certainly cant make a living by kissing girls! 转载于:https://my.oschina.net/u/553266/blog/75…

【Codeforces】158B-Taxi(贪心,怎么贪咧)
贪心 emmmm http://codeforces.com/contest/158/problem/B 题目大意:有四种旅客,四人一组,三人一组,两人一组,一人一组,一辆出租车最多可以坐四个人,并且一组里的人必须坐一辆车,…

90 后 CTO 创业 6 年,做了一件改变互联网的“小事”
TGO 鲲鹏会在武汉举行了一场线下分享活动 —— 冲破壁垒,打造精英的技术团队 。来自极验的 90 后 CTO 黄胜蓝分享了他的团队故事,以及在他看来一个创新团队应该具备的特征。极验 CTO \u0026 TGO 鲲鹏会会员黄胜蓝在现场进行分享 1. 创新:非典…





