TCP/IP 协议(Transmission Control Protocol / internet Protocol),因特网互联协议,又名网络通讯协议。通俗而言:TCP负责发现传输的问题,一有问题就发出信号,要求重新传输,直到所有数据安全正确地传输到目的地。而IP是给因特网的每一台联网设备规定一个地址。
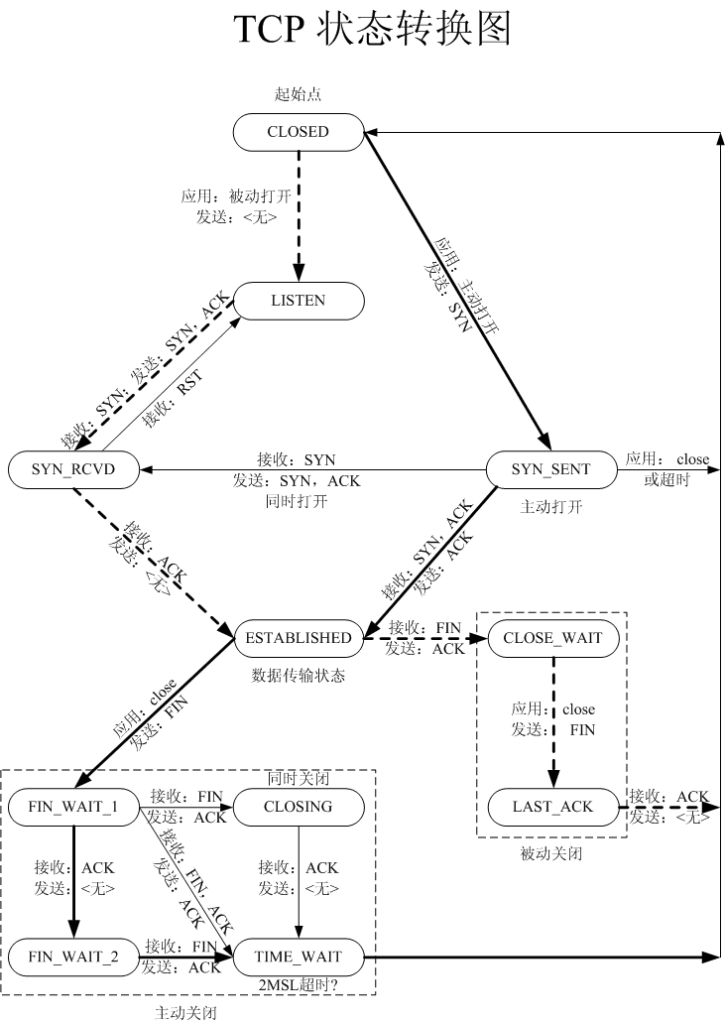
TCP是面向连接的通信协议,通过三次握手建立连接,通讯完成时要拆除连接,由于TCP是面向连接的所以只能用于端到端的通讯。
TCP提供的是一种可靠的数据流服务,采用“带重传的肯定确认”技术来实现传输的可靠性。TCP还采用一种称为“滑动窗口”的方式进行流量控制,所谓窗口实际表示接收能力,用以限制发送方的发送速度。
三次握手(three times handshake;three-way handshake)所谓的“三次握手”即对每次发送的数据量是怎样跟踪进行协商使数据段的发送和接收同步,根据所接收到的数据量而确定的数据确认数及数据发送、接收完毕后何时撤消联系,并建立虚连接。为了提供可靠的传送,TCP在发送新的数据之前,以特定的顺序将数据包的序号,并需要这些包传送给目标机之后的确认消息。TCP总是用来发送大批量的数据。当应用程序在收到数据后要做出确认时也要用到TCP。
第一次握手:建立连接时,客户端发送syn包(syn=j)到服务器,并进入SYN_SENT状态,等待服务器确认;SYN:同步序列编号
第二次握手:服务器收到syn包,必须确认客户的SYN(ack=j+1),同时自己也发送一个SYN包(syn=k),即SYN+ACK包,此时服务器进入SYN_RECV状态;
第三次握手:客户端收到服务器的SYN+ACK包,向服务器发送确认包ACK(ack=k+1),此包发送完毕,客户端和服务器进入ESTABLISHED状态,完成三次握手。
我在这里举个例子:比如 客户端A 有一天给 服务器 B发了一个快递,但是服务器B不知道,当收到快递时,服务器B给客户端A打了一个电话问是否给我发了一个快递,然后客户端A告诉服务器B,是给他发了一个。然后服务器B挂了电话,拿到快递,签字。