拜托,面试别再问我时间复杂度了!!!
最烦面试官问,“为什么XX算法的时间复杂度是OO”,今后,不再惧怕这类问题。
快速排序分为这么几步:
第一步,先做一次partition;

partition使用第一个元素t=arr[low]为哨兵,把数组分成了两个半区:、
● 左半区比t大
● 右半区比t小
第二步,左半区递归;
第三步,右半区递归;
伪代码为:
void quick_sort(int[]arr, int low, int high){
if(low== high) return;
int i = partition(arr, low, high);
quick_sort(arr, low, i-1);
quick_sort(arr, i+1, high);
}
为啥,快速排序,时间复杂度是O(n*lg(n))呢?
今天和大家聊聊时间复杂度。
画外音:往下看,第三类方法很牛逼。
第一大类,简单规则
为方便记忆,先总结几条简单规则,热热身。
规则一:“有限次操作”的时间复杂度往往是O(1)。
例子:交换两个数a和b的值。
void swap(int& a, int& b){
int t=a;
a=b;
b=t;
}
分析:通过了一个中间变量t,进行了3次操作,交换了a和b的值,swap的时间复杂度是O(1)。
画外音:这里的有限次操作,是指不随数据量的增加,操作次数增加。
规则二:“for循环”的时间复杂度往往是O(n)。
例子:n个数中找到最大值。
int max(int[] arr, int n){
int temp = -MAX;
for(int i=0;i<n;++i)
if(arr[i]>temp) temp=arr[i];
return temp;
}
分析:通过一个for循环,将数据集遍历,每次遍历,都只执行“有限次操作”,计算的总次数,和输入数据量n呈线性关系。
规则三:“树的高度”的时间复杂度往往是O(lg(n))。
分析:树的总节点个数是n,则树的高度是lg(n)。
在一棵包含n个元素二分查找树上进行二分查找,其时间复杂度是O(lg(n))。
对一个包含n个元素的堆顶元素弹出后,调整成一个新的堆,其时间复杂度也是O(lg(n))。
第二大类:组合规则
通过简单规则的时间复杂度,来求解组合规则的时间复杂度。
例如:n个数冒泡排序。
void bubble_sort(int[] arr, int n){
for(int i=0;i<n;i++)
for(int j=0;j<n-i-1;j++)
if(arr[j]>arr[j+1])
swap(arr[j], arr[j+1]);
}
分析:冒泡排序,可以看成三个规则的组合:
1. 外层for循环
2. 内层for循环
3. 最内层的swap
故,冒泡排序的时间复杂度为:
O(n) * O(n) * O(1) = O(n^2)
又例如:TopK问题,通过建立k元素的堆,来从n个数中求解最大的k个数。

先用前k个元素生成一个小顶堆,这个小顶堆用于存储,当前最大的k个元素。

接着,从第k+1个元素开始扫描,和堆顶(堆中最小的元素)比较,如果被扫描的元素大于堆顶,则替换堆顶的元素,并调整堆,以保证堆内的k个元素,总是当前最大的k个元素。

直到,扫描完所有n-k个元素,最终堆中的k个元素,就是为所求的TopK。
伪代码:
heap[k] = make_heap(arr[1, k]);
for(i=k+1 to n){
adjust_heap(heep[k],arr[i]);
}
return heap[k];
分析:可以看成三个规则的组合:
1. 新建堆
2. for循环
3. 调整堆
故,用堆求解TopK,时间复杂度为:
O(k) + O(n) * O(lg(k)) = O(n*lg(k))
画外音:注意哪些地方用加,哪些地方用乘;哪些地方是n,哪些地方是k。
第三大类,递归求解
简单规则和组合规则可以用来求解非递归的算法的时间复杂度。对于递归的算法,该怎么分析呢?
接下来,通过几个案例,来说明如何通分析递归式,来分析递归算法的时间复杂度。
案例一:计算 1到n的和,时间复杂度分析。
如果用非递归的算法:
int sum(int n){
int result=0;
for(int i=0;i<n;i++)
result += i;
return result;
}
根据简单规则,for循环,sum的时间复杂度是O(n)。
但如果是递归算法,就没有这么直观了:
int sum(int n){
if (n==1) return 1;
return n+sum(n-1);
}
如何来进行时间复杂度分析呢?
用f(n)来表示数据量为n时,算法的计算次数,很容易知道:
● 当n=1时,sum函数只计算1次
画外音:if (n==1) return 1;
即:
f(1)=1【式子A】
不难发现,当n不等于1时:
● f(n)的计算次数,等于f(n-1)的计算次数,再加1次计算
画外音:return n+sum(n-1);
即:
f(n)=f(n-1)+1【式子B】
【式子B】不断的展开,再配合【式子A】:
画外音:这一句话,是分析这个算法的关键。
f(n)=f(n-1)+1
f(n-1)=f(n-2)+1
…
f(2)=f(1)+1
f(1)=1
上面共n个等式,左侧和右侧分别相加:
f(n)+f(n-1)+…+f(2)+f(1)
=
[f(n-1)+1]+[f(n-2)+1]+…+[f(1)+1]+[1]
即得到:
f(n)=n
已经有那么点意思了哈,再来个复杂点的算法。
案例二:二分查找binary_search,时间复杂度分析。
int BS(int[] arr, int low, int high, int target){
if (low>high) return -1;
mid = (low+high)/2;
if (arr[mid]== target) return mid;
if (arr[mid]> target)
return BS(arr, low, mid-1, target);
else
return BS(arr, mid+1, high, target);
}
二分查找,单纯从递归算法来分析,怎能知道其时间复杂度是O(lg(n))呢?
仍用f(n)来表示数据量为n时,算法的计算次数,很容易知道:
● 当n=1时,bs函数只计算1次
画外音:不用纠结是1次还是1.5次,还是2.7次,是一个常数次。
即:
f(1)=1【式子A】
在n很大时,二分会进行一次比较,然后进行左侧或者右侧的递归,以减少一半的数据量:
● f(n)的计算次数,等于f(n/2)的计算次数,再加1次计算
画外音:计算arr[mid]>target,再减少一半数据量迭代
即:
f(n)=f(n/2)+1【式子B】
【式子B】不断的展开,
f(n)=f(n/2)+1
f(n/2)=f(n/4)+1
f(n/4)=f(n/8)+1
…
f(n/2^(m-1))=f(n/2^m)+1
上面共m个等式,左侧和右侧分别相加:
f(n)+f(n/2)+…+f(n/2^(m-1))
=
[f(n/2)+1]+[f(n/4)+1]+…+[f(n/2^m)]+[1]
即得到:
f(n)=f(n/2^m)+m
再配合【式子A】:
f(1)=1
即,n/2^m=1时, f(n/2^m)=1, 此时m=lg(n), 这一步,这是分析这个算法的关键。
将m=lg(n)带入,得到:
f(n)=1+lg(n)
神奇不神奇?
最后,大boss,快速排序递归算法,时间复杂度的分析过程。
案例三:快速排序quick_sort,时间复杂度分析。
void quick_sort(int[]arr, int low, inthigh){
if (low==high) return;
int i = partition(arr, low, high);
quick_sort(arr, low, i-1);
quick_sort(arr, i+1, high);
}
仍用f(n)来表示数据量为n时,算法的计算次数,很容易知道:
● 当n=1时,quick_sort函数只计算1次
f(1)=1【式子A】
在n很大时:
第一步,先做一次partition;
第二步,左半区递归;
第三步,右半区递归;
即:
f(n)=n+f(n/2)+f(n/2)=n+2*f(n/2)【式子B】
画外音:
(1)partition本质是一个for,计算次数是n;
(2)二分查找只需要递归一个半区,而快速排序左半区和右半区都要递归,这一点在分治法与减治法一章节已经详细讲述过;
【式子B】不断的展开,
f(n)=n+2*f(n/2)
f(n/2)=n/2+2*f(n/4)
f(n/4)=n/4+2*f(n/8)
…
f(n/2^(m-1))=n/2^(m-1)+2f(n/2^m)
上面共m个等式,逐步带入,于是得到:
f(n)=n+2*f(n/2)
=n+2*[n/2+2*f(n/4)]=2n+4*f(n/4)
=2n+4*[n/4+2*f(n/8)]=3n+8f(n/8)
=…
=m*n+2^m*f(n/2^m)
再配合【式子A】:
f(1)=1
即,n/2^m=1时, f(n/2^m)=1, 此时m=lg(n), 这一步,这是分析这个算法的关键。
将m=lg(n)带入,得到:
f(n)=lg(n)*n+2^(lg(n))*f(1)=n*lg(n)+n
故,快速排序的时间复杂度是n*lg(n)。
wacalei,有点意思哈!
画外音:额,估计83%的同学没有细究看,花5分钟细思上述过程,一定有收获。
总结
● for循环的时间复杂度往往是O(n)
● 树的高度的时间复杂度往往是O(lg(n))
● 二分查找的时间复杂度是O(lg(n)),快速排序的时间复杂度n*(lg(n))
● 递归求解,未来再问时间复杂度,通杀
知其然,知其所以然。
思路比结论重要。
原文发布时间为:2018-10-8
本文作者:58沈剑
本文来自云栖社区合作伙伴“架构师之路”,了解相关信息可以关注“架构师之路”。
相关文章:

C#和JavaScript的简单互交
转自:http://cgxcn.blog.163.com/blog/static/132312422009426112558831/ 1.asp.net呼叫js Response.Write("<script languagejavascript>"); Response.Write("alert(登峰欢迎您 );" ); …

读阮一峰对《javascript语言精粹》的笔记,我有疑问。
《javascript语言精粹》是一本很棒的书籍,其中作者在附录列出了12种他所认为的javascript语言中的糟粕。 我最近开始跟读前端前辈的博客,其中读到了阮一峰的《12种不宜使用的Javascript语法》,有一个疑问: 文如下: 9. …

1008 Elevator
思路如下:用一个整型数组存楼层,0号元素为0(开始停在0层),每读入一个元素,和上一个比较,更大说明是上升,总时长加上楼层差*6,反之说明是下降,总时长加上楼层差*4。最后再管停留时间&…

软件安全性能測试(转载)
近来,在我负责的公司某软件产品的最后測试工作,经常被问到这样一个问题:在做測试过程中,我们的软件产品在安全性方面考虑了多少?应该怎样測评一个软件究竟有多安全? 这个软件因为涉及客户商业上重要的…

org.springframework.data.redis 一次连接获取特定key所有k-v(pipeline)
2019独角兽企业重金招聘Python工程师标准>>> 当我们需要一次性获取在redis中以hash方式存储的所有key-value时,我们可以使用下面的方式来获取。 public void testGetMore() throws IOException {RedisCallback<List<Object>> pipelineCallba…

[网络应用]Flash中鼠标手势及Ctrl+T问题{Firefox}
想说这个问题很久了,也是对Flash的一点点小小的不满。 当你在浏览youku,56,Youtube,土豆,Kou6上的视频时,是不是会发现你的CtrlT命令不凑效了。 当你在打开一个Flash全站时,或者鼠标焦点在一个令…

(C++)一行代码递归实现辗转相除法
定理:两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。 int gcd(int a,int b){return !b?a:gcd(b,a%b); } 这里递归边界是 gcd(a,0)a; 递归式是 gcd(a,b)gcd(b,a%b);

【C#】Web页面传值小结-
1. 使用QueryString变量 QueryString是一种非常简单的传值方式,他可以将传送的值显示在浏览器的地址栏中。如果是传递一个或多个安全性要求不高或是结构简单的数值时,可以使用这个方法。但是对于传递数组或对象的话,就不能用这个方法了…

分享:用promise封装ajax
用promise封装ajaxvar ajaxOptions {url: url,method: GET,async: true,data: null,dataType: text, } function ajax(protoOptions) {var options {};for(var i in ajaxOptions){options[i] protoOptions[i] || ajaxOptions[i];}return new Promise(function(resolve, reje…

1049 Counting Ones
1. 这一题起初我用递归的方式,还写了一个数整数有多少个1的函数,OneNum[i] OneNum[i-1]countOne(i);毫不意外地出现了段错误,也就是递归调用的次数太多。 2. 看了参考书,得到了思路上的启发: 给定一个数12ÿ…

Oracle:递归查询(树形结构数据)
今天要做一个查询功能:查询某用户所属部门,且包含该部门的所有上级部门信息。偶然找到了一个方法,特意来做个笔记。分享给和我一样的菜鸟,哈哈 查询子节点 1 select * 2 from d_arc_dep 3 start with depid 100000 4 connect b…
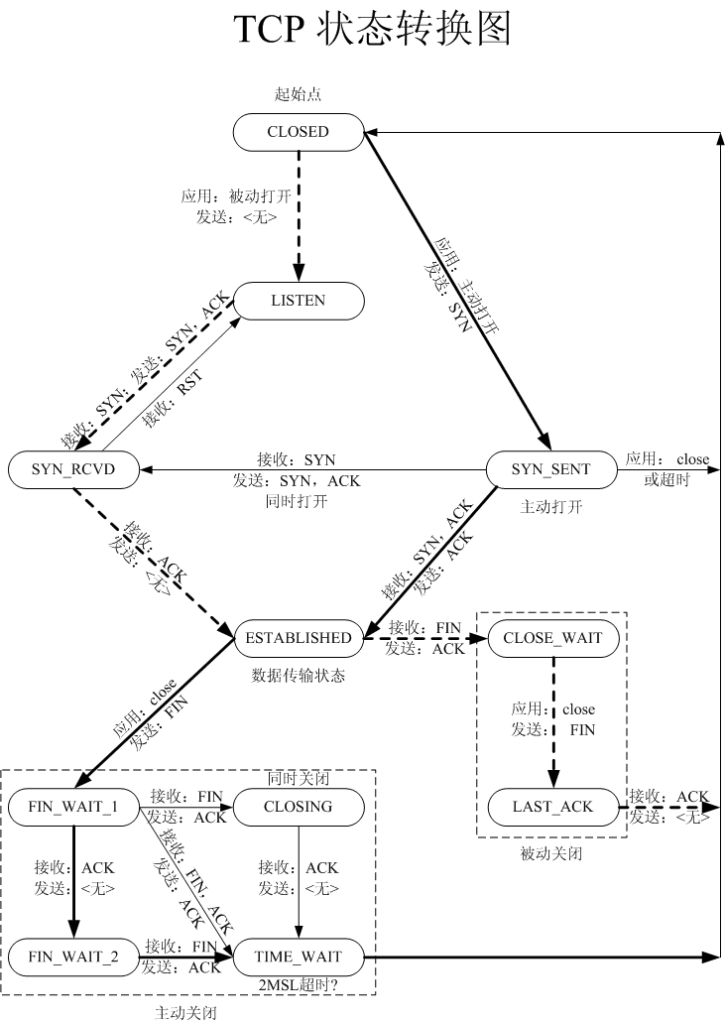
FIN_WAIT_2
来自转载:http://blog.sina.com.cn/s/blog_8e5d24890102w9yi.html 上图对排除和定位网络或系统故障时大有帮助,但是怎样牢牢地将这张图刻在脑中呢?那么你就一定要对这张图的每一个状态,及转换的过程有深刻地认识,不能只…

网页制作知识:XHTML 和 DOCTYPE 切换
为 Web页指定 DOCTYPE 会影响浏览器呈现页的方式。Internet Explorer、Mozilla Firefox 和 Opera 全都支持一种名为“DOCTYPE 切换”(也叫“DOCTYPE 嗅探”)的功能。 引入 DOCTYPE 切换的目的是使浏览器能够正确地呈现符合标准的 Web 站点以及旧式 Web 站…

1003 我要通过!
1. 总体思路是自己先写写,看看哪些字符串符合,找出规律,然后根据测试用例来矫正。 2. 用到了递推的方法,我使用countA[maxn]数组存放截至当前位置一共出现的A的个数。 3. 正确的字符串满足的条件是:P之前A的个数P和T…

微信电视来了 微信遥控传屏弹幕统统有
据证券时报消息,腾讯携手康佳推微信电视,具有微信传屏、微信弹幕、微信遥控等基于腾讯微信平台的电视功能。想了吧?别急,11月5日,微信互联电视将在康佳全国终端门店全部上线。微信电视2.0版将新增语音搜索、节目单分享…

机器学习-线性回归LinearRegression
概述 今天要说一下机器学习中大多数书籍第一个讲的(有的可能是KNN)模型-线性回归。说起线性回归,首先要介绍一下机器学习中的两个常见的问题:回归任务和分类任务。那什么是回归任务和分类任务呢?简单的来说,…

使用Windows的SHFileOperation外壳函数实现文件操作
在Windows的shellapi文件中定义了一个名为SHFileOperation()的外壳函数,用它可以实现各种文件操作,如文件的拷贝、删除、移动等,该函数使用起来非常简单,它只有一个指向SHFILEOPSTRUCT结构的参数。使用SHFi…

(C++)寻找1-100以内所有素数,复杂度为O(nsqrt(n))与O(nloglogn)的两种方法
注意:1既不是质数也不是合数,2是质数。 1. 复杂度为O(nsqrt(n)) 原理:先写一个判断整数是否为素数的函数,其复杂度为sqrt(n),其原理是对于一个数n,如果它有除了1和自身之外的因子,那么这个因子…

这样就算会了PHP么?-10
关于基本的文件读写内容: <?phpecho "readfile function:<br>";readfile("tm.txt");echo "<br>";echo "file function:<br>";$f_arr file("tm.txt");foreach ($f_arr as $cont) {echo $c…

个人项目-小学四则运算 “软件”之初版
本次作业要求来自:https://edu.cnblogs.com/campus/gzcc/GZCC-16SE1/homework/2166 我的github远程仓库的地址:https://github.com/yanyuluu/yanyuluu/tree/master/ruanjiangc 第一部分:要求 具体要求:任何编程语言都可以…
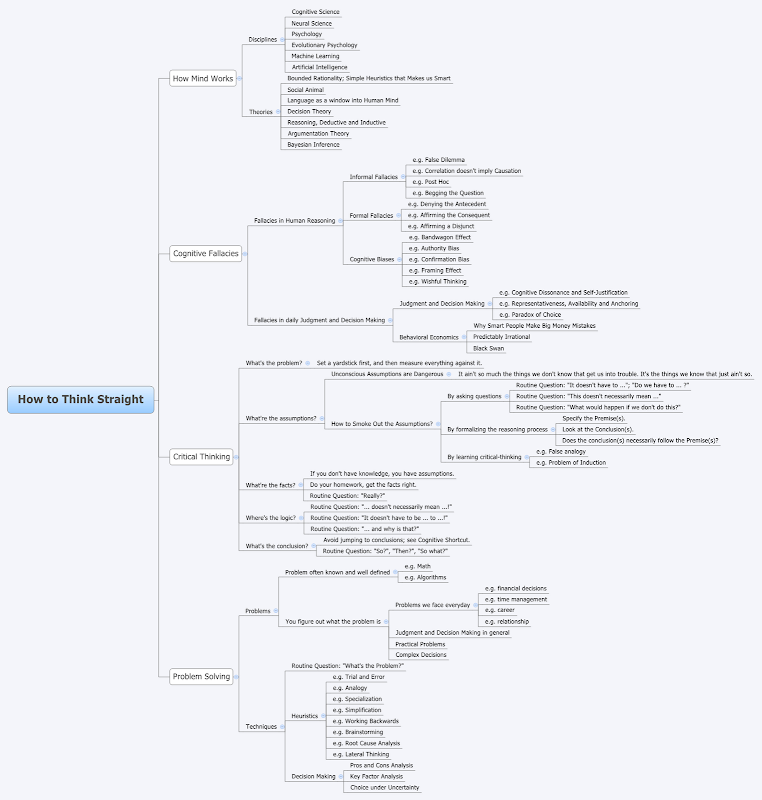
如何清晰地思考
如何清晰地思考(近一年来业余阅读的关于思维方面的知识结构整理) Tags: 思维改变生活save it16 saved tags: thinking mind 思考 一年前一个偶然的机会我遇到了一本书——《影响力》,看完这本书之后对我们如何思维产生了极大的兴趣&…

1015 Reversible Primes
1. 这道题因为一上来看到又是进制的转换又是素数的判断,想到自己十进制转化成Q进制的除基取余掌握得并不好,就很紧张,以为要封装一堆函数,然后我也确实这么做了,经过一堆调试(字符和数字之间转化容易忘记),…

跨平台表空间传输(摘自eygle《循序渐进Oracle》)
需要注意的是,在Oracle 10g之前,数据文件是不能够跨平台传输使用的,从Oracle 10g开始,Oracle支持跨平台的表空间传输,这极大地增强了数据迁移的便利性。 1. 字节顺序和平台 数据文件所以不能跨平台,主要是…

EditPlus集成Java编译和运行命令组建轻量级Java SE开发工具
http://www.gogogogo.me/development/EditPlus-Java.html转载于:https://www.cnblogs.com/svennee/p/4071712.html

单例测试模式中【饿汉式】与【懒汉式】的区别
package day25.thread;/** /*** author Mr Chen* create 2018-10-09 18:37* 单例测试模式:保证类在内存中只有一个对象*/ public class Dome01 {public static void main(String[] args){Singleton s1 Singleton.s; //成员变量被私有…

1078 Hashing
关键在于这句:Quadratic probing (with positive increments only) is used to solve the collisions.开始不懂二次探测,因此做不出来。所谓二次探测就是如果num%mSize被占坑了,就看看(num1*1)%mSize有没有被占,还是被占ÿ…

C# 多线程 参数传递
class ThreadDemo { private Thread[] threads; private int thrs 10;//线程数量 private ArrayList stringList; private event EventHandler OnNumberClear;//数据删除完引发的事件 public ThreadDemo(int number) …

Android 中自定义控件和属性(attr.xml,declare-styleable,TypedArray)的方法和使用
一、 在res/values 文件下定义一个attrs.xml 文件.代码如下: <?xml version"1.0" encoding"utf-8"?> <resources> <declare-styleable name"MyView"> <attr name"textColor" format"color…

排序学习之---快速排序
一、前言 快速排序是一种交换排序,它由C. A. R. Hoare在1962年提出。 二、算法思想 快速排序的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数。 然后再按此方法对这两部…

1059 Prime Factors
1. 第一次测试点三错误,由于1既不是质数也不是合数,因此对于1来说需要有一个特殊判断,输出:11,但是一开始多加了一个等号。 2. 本题需要数学基础好,两个重点: (1)会打印某个范围内的素数表 (…
