如何清晰地思考(近一年来业余阅读的关于思维方面的知识结构整理)
一年前一个偶然的机会我遇到了一本书——《影响力》,看完这本书之后对我们如何思维产生了极大的兴趣,于是在一年的时间里面密集地阅读了以下一些方面的经典著作:社会心理学、认知科学、神经科学、进化心理学、行为经济学、机器学习、人工智能、自然语言处理、问题求解、辩论法(Argumentation Theory)、Critical Thinking、判断与决策。以及大量的 Wikipedia 条目。
这一年来,对以上这些领域的阅读和思考给我带来了极大的价值,我相信他们也会给你带来巨大的收益。
关于为什么我认为我们都需要学习这方面的知识,我曾在博客中写到:
另外还有一些我认为是 essential knowledge 的例子:分析问题解决问题的思维方法(这个东西很难读一两本书就掌握,需要很长时间的锻炼和反思)、判断与决策的方法(生活中需要进行判断与决策的地方远远多于我们的想象),波普尔曾经说过:All Life is Problem-Solving。而判断与决策又是其中最常见的一类Problem Solving。尽管生活中面临重大决策的时候并不多,但另一方面我们时时刻刻都在进行最重大的决策:如:决定自己的日常时间到底投入到什么地方去。如:你能想象有人宁可天天花时间剪报纸上的优惠券,却对于房价的1%的优惠无动于衷吗?(《别做正常的傻瓜》、《Predictably Irrational》)如:你知道为什么当手头股票的股价不可抑止地滑向深渊时我们却一边揪着头发一边愣是不肯撤出吗?(是的,我们适应远古时代的心理机制根本不适应金融市场。)糟糕的判断与决策令我们的生活变得糟糕,这还不是最关键的,最关键的是我们从来不会去质疑自己的判断,而是总是能“找到”其他为自己辩护的理由(《错不在我(Mistakes were made, but not by me)》)又,现在是一个信息泛滥的时代,于是另一个问题也出现:如何在海洋中有效筛选好的信息,以及避免被不好的信息左右我们的大脑(Critical Thinking)关于以上提到的几点我在豆瓣上有一个专门的豆列(“学会思考”),希望有一天我能够积累出足够多的认识对这个主题展开一些详细介绍。
人类的大脑和思维是目前已知最为复杂的系统,对这个系统的研究不仅自身是一件极其迷人的事情,对于像我们这样的芸芸众生来说即便不去做研究,学习一些这方面的科普知识,对于学会正确地思考有极大的益处。
你的大脑是你唯一的工具,要正确利用这个工具,唯一的途径就是去了解它。与很多人的直觉相反,实际上我们的思维有着各种各样的缺陷和陷阱(keyword: cognitive bias),我们解决日常问题的思维方式也并不总是最优的(keyword: bounded rationality),这里摘抄一段我在豆列上的导言:
我们的思维有很多很多的弱点,我一向认为,正确的思维方式,是一切高效学习的基础。比如参见如下2个例子,错误的思维方式得到的结论有大得多的可能性是谬误。
- 人总喜欢沿袭以往习得的经验,并通过类比来进行外推。我第一次在一个地铁终点站坐地铁的时候,看着从远方开来的地铁,我心生疑惑——“这车每节车厢都这么长,待会怎么调头呢(我心说没看到铁轨终点有一个大大的供调头的 U 形弯啊)?”,当车开始开的时候我终于意识到原来车是可以往两头方向开的。
- 人喜欢从关联当中寻找因果,有一次我我老婆去银行取款,到了 ATM 室的自动门口,我开玩笑地拿着手头的饭卡去刷了一下,然后——门居然开了。我顿时来了劲,立即得出一个结论:这个刷卡装置不安全,至少不是能够专门识别银联的卡的。我甚至飞快地泛化出了一个更具一般性的理论来解释这个现象:即可能所有带有磁性的卡都可以用来开门。老婆看我得意洋洋,就泼过来一盘冷水:不一定是你的卡刷开的啊,你不刷卡试试看。我不信,说怎么可能呢,心想我刷卡,门就开了,还有比这更明显的因果关系嘛。但出乎我意料的是,我走出门,这次没刷卡,门也开了——原来是感应门——原先这个 ATM 室的确是刷卡门,但后来改成了感应门,刷卡的那个装置只不过没拆掉残留在那里而已。
总的来说
- 人类的思维充满着各种各样的捷径,每一条捷径都是一把双刃剑。一方面,它降低了大脑的认知复杂性(笼统的看一个问题要比细致的分析简单得多),有助于迅速做出绝大部分时候都正确的判断;但另一方面,它也常常导致人们把大部分情况下成立的法则当成了放之四海而皆准的。可以说,有多少捷径,就有多少条谬误。
- 人类的情绪也在很大程度上影响着人的思考。比如,如果你憎恶一个人,你往往就会反对他的所有立场。反之亦成立。
- 人类大脑经过长时间的进化,先天就具备一些特定的“思维定势”,以使得人类能够在面对进化过程中经常出现的适应性问题时能够不假思索的做出迅速的反应。然而,在现代社会,这类思维定势已经不适应了。
- 人类不可避免的受着各种各样的偏见的影响,这些偏见有些是有一定适应价值的“思维定势”(如事后聪明式偏见),而有些则是大脑的认知机制的“缺陷”。
以上,构成了人类思维中的种种谬误。而学会思考,就是学会认识到这些谬误。
Critical-Thinking 在西方拥有悠久的历史,早到古希腊时代,亚里士多德就已经对人类语言中的各种各样的谬误有了一定的认识(譬如,“我们无法讨论不存在的东西,所以所有的事物都是真实的”),并对辩论之中存在的各种各样的谬误进行了归类。然而令人遗憾的是,在中国的文化里面,理性思维似乎是一直被抑制的,中国文人传统都是非理性思考者;所谓非理性思考,主要包括联想、比方等形式,这些思维方式作为人类天生具有的思维方式的一种,一方面当然有它的好处(比如在科研方面,联想往往能够启发新思路;类比也有助于用新颖的方式来解决既有问题),然而另一方面,这样的思维方式同样也充满了各种各样致命的谬误。在大众知识领域,自中国古代文人思维习惯流传下来的影响深刻地左右着人们的语言习惯,随处可见的不靠谱的类比和文字游戏就是证明(例如,严格来说,类比的一般形式是,A具有X、Y、Z三个属性,B具有X、Y属性(类似于A),所以B具有Z属性。这个类比要成立,必须要满足一个前提,即X、Y属性对于Z属性的有无必须是有关的。然而这个前提被根本忽视了,详见 False Analogy)。
这个豆列中的书,有一些是介绍人类思维工作的机制的,认识这些机制是正确思考的大前提;有许多是关于人类推理(Reasoning)过程中的形形色色的谬误的,因为唯有认识到 这些谬误,才能避免它们。唯有避免了思维的谬误,才能进行正确的思考。
注:
- 一个最完整的认知偏见(cognitive bias)列表见:http://en.wikipedia.org/wiki/List_of_cognitive_biases
- 一个完整的 Fallacies 列表见: http://en.wikipedia.org/wiki/Fallacies
- Wikipedia 上关于 Critical Thinking 的条目见: http://en.wikipedia.org/wiki/Critical_thinking
另:
- 人类在思考问题的过程中,自身的思维习惯、性格、知识积累无不都在悄悄地影响着思维的过程,所以,一些心理学的知识也非常有助于帮助正确的思考。更多心理学方面的推荐,参考:http://www.douban.com/doulist/46003/
文章末尾将贴出的是我这一年来学习的知识结构总揽(用 XMind 画的思维导图)。注:这只是一个整体的知识结构,或者说“寻路图”,其中固然包含一些例子(用 “e.g.” 标出),但最重要的是从各个分支引申出去的延伸阅读,后者包含上百个很有价值的 wikipedia 条目,不下 50 本经典的著作(大部分我已经读过,小部分经过我的仔细考察,正在阅读中或者肯定是有价值的)。
如何获得这些延伸出去的阅读,有两个办法:
1. 在总揽图中抽出关键字到 Wikipedia&Google 上查找,如:informal fallacy,cognitive biases,bounded rationality, critical thinking, argumentation theory, behavioral economics, problem solving 等等(以上这些关键字你都会在思维导图中看到)。注:阅读 Wikipedia 时要严重注意每个条目后面的 Reference ,一般来说这些参考资料本身也都非常经典,其价值不亚于 Wikipedia 条目本身。
2. 查看我整理的四个豆列:
- 【只读经典】心理学改变生活
- 【只读经典】学会思考
- 【只读经典】判断与决策
- 机器学习与人工智能学习资源导引
以上四个豆列中整理的绝大多数都是我阅读过的,你也可以参考我的整个“思维”标签下的书。如何获得这些书(尤其是其中包含大量的无中文翻译版的英文书)请参考李笑来老师的笔记。
这个领域的新知识是如此的纷至沓来,以至于我只有时间不断地阅读和思考,以及不时在我的 Google Notebook 里做一些笔记,而完全没有时间一本书一本书,一个子领域一个子领域地写具体的 Introduction (目前具体的荐书只是在 TopLanguage 上零散的推荐了几本,还没有专题介绍)。既便如此,仍然还是在博客上写了很多相关的东西,它们就是这一年来的学习的收获的证明:-),因此如果你想快速判断上面列出的一些书籍是否对你有价值,有多大的价值,不妨参考一下我写的这些文章,这些文章很大程度上是在这一年的学习过程当中的感悟或总结。注:第 3 部分(关于学习、记忆与思考)的文章基本上是领域无关的:
关于 Problem Solving 的
- 《跟波利亚学解题》
- 《知其所以然地学习(以算法学习为例)》
关于机器学习的(机器学习和人工智能领域对于理解我们的思维方式也提供了极好的参考)
- 《数学之美番外篇:平凡而又神奇的贝叶斯方法》
- 《机器学习与人工智能学习资源导引》
关于学习、记忆与思考的
- 《一直以来伴随我的一些学习习惯》(一,二,三,四)
- 《方法论、方法论——程序员的阿喀琉斯之踵》
- 《学习与记忆》
- 《阅读与思考》
- 《鱼是最后一个看到水的》
- 《我不想与我不能》
- 《学习密度与专注力》
好在我并不打算零星的一本一本推荐:D 所以我就花了点时间将整个的知识体系整理了一番,画了下面这张结构图,请按图索骥,如下(有三个版本,1. 至 xMind Share 的超链接,2. 内嵌在该页面中的幻灯片,如果无法载入请参考 1 。3. 图片版(注:图很大,请下载浏览或打印))
我在前面写学习习惯的时候曾经提到:
8. 学习一项知识,必须问自己三个重要问题:1. 它的本质是什么。2. 它的第一原则是什么。3. 它的知识结构是怎样的。
有朋友问我具体的例子,好吧,那么这张思维导图便是第三点——知识结构——的一个很好的例子:)
1. 至 XMind Share 的超链接:http://share.xmind.net/pongba/how-to-think-straight-4/
2. 嵌入的幻灯片(如加载失败请直接点击上面的 XMind Share 超链接至 XMind 浏览):
3. 图片版(此为缩略版,完整版请至相册下载:google picasa 的 ,或 csdn 相册的)(最后提醒一下,别忘了这幅图只是大量书籍和 Wikipedia 条目的“藏宝图”,如何延伸阅读请参考前文所述的方法)
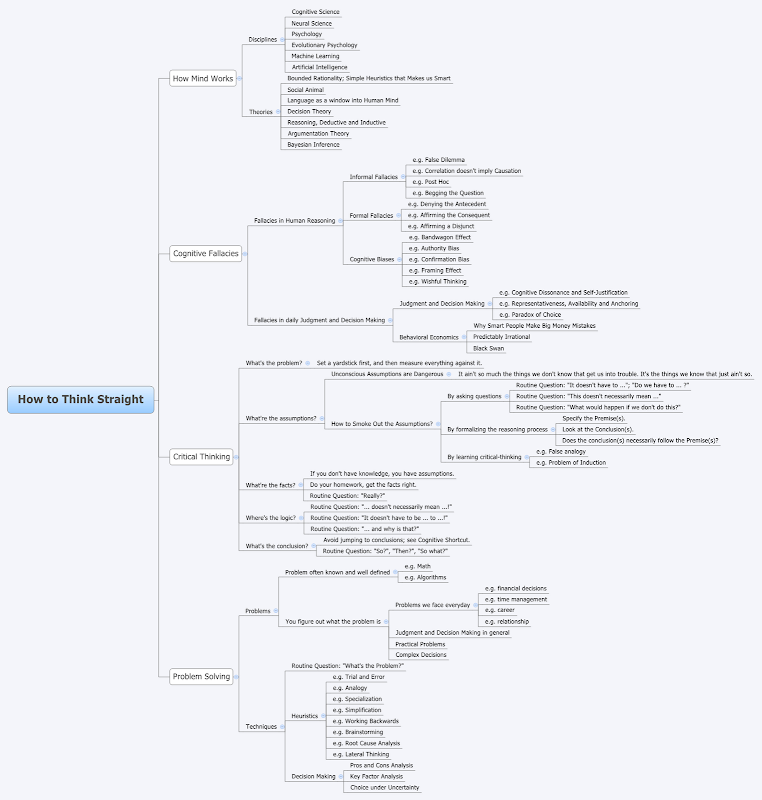 |
| From XMind |







