(C++)寻找1-100以内所有素数,复杂度为O(nsqrt(n))与O(nloglogn)的两种方法
注意:1既不是质数也不是合数,2是质数。
1. 复杂度为O(nsqrt(n))
原理:先写一个判断整数是否为素数的函数,其复杂度为sqrt(n),其原理是对于一个数n,如果它有除了1和自身之外的因子,那么这个因子要么成对出现,一个在(1,sqrt(n)),另一个在(sqrt(n),n)。要么为sqrt(n)。因此只要判断(1,sqrt(n)]范围内有没有因子就好了。
判断函数的两种写法如下
bool isPrime(int n){if(n<=1)return false;//特判 for(int i=2;i<=(int)sqrt(1.0*n);i++){if(n%i==0)return false;}return true;
}说明:sqrt得到的结果为浮点型,强制转化为整型是对其向下取整
注意:i从2开始遍历
bool isPrime(int n){if(n<=1)return false;//特判 for(int i=2;i*i<=n;i++){if(n%i==0)return false;}return true;
}注意:i*i可能溢出,最好声明i为long long型。
2. 复杂度为O(nloglogn)
原理:用一个长度为101的布尔数组,存放1-100这100个数字是否为素数。从2开始,遇到一个素数,就把这个素数在100以内的所有倍数都初始化为false。
int main(){bool isPrime[maxn] = {0};//maxn = 101,默认都是素数,再筛去不是的 isPrime[2] = 0;for(int i=2;i<maxn;i++){if(!isPrime[i]){for(int j=i+i;j<maxn;j+=i){isPrime[j] = true;}}} return 0;
}注意学习这里碰到一个素数,找它的倍数的方法。
还有一个很重要的一点,一开始我困惑不是筛出吗?那不应该一开始全部初始化为true吗?但是请注意了,给数组统一初始化只能是0,不能是1,因此只能绕个弯用0来表示这个数是素数。
相关文章:

这样就算会了PHP么?-10
关于基本的文件读写内容: <?phpecho "readfile function:<br>";readfile("tm.txt");echo "<br>";echo "file function:<br>";$f_arr file("tm.txt");foreach ($f_arr as $cont) {echo $c…

个人项目-小学四则运算 “软件”之初版
本次作业要求来自:https://edu.cnblogs.com/campus/gzcc/GZCC-16SE1/homework/2166 我的github远程仓库的地址:https://github.com/yanyuluu/yanyuluu/tree/master/ruanjiangc 第一部分:要求 具体要求:任何编程语言都可以…
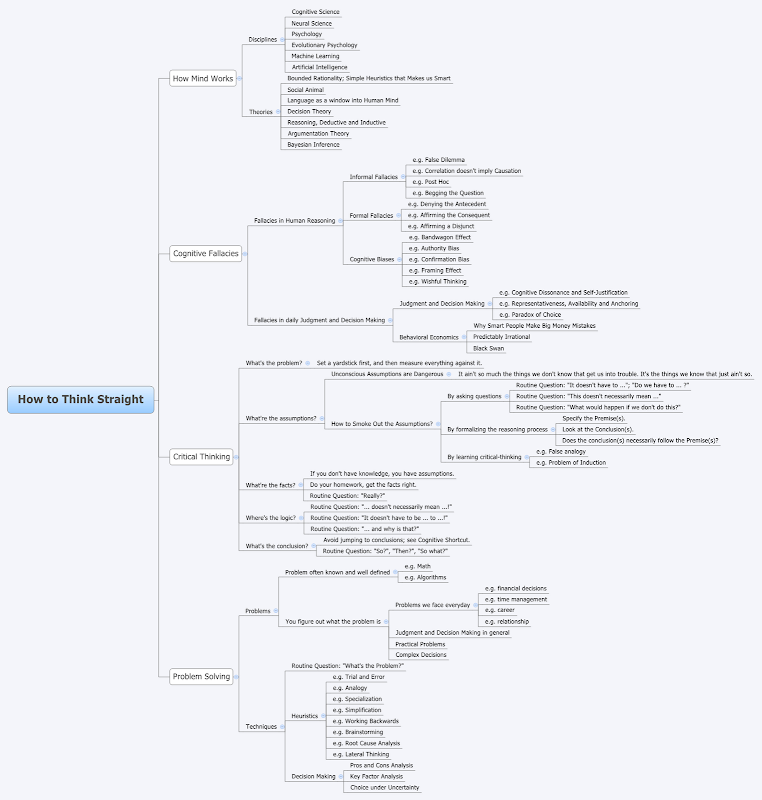
如何清晰地思考
如何清晰地思考(近一年来业余阅读的关于思维方面的知识结构整理) Tags: 思维改变生活save it16 saved tags: thinking mind 思考 一年前一个偶然的机会我遇到了一本书——《影响力》,看完这本书之后对我们如何思维产生了极大的兴趣&…

1015 Reversible Primes
1. 这道题因为一上来看到又是进制的转换又是素数的判断,想到自己十进制转化成Q进制的除基取余掌握得并不好,就很紧张,以为要封装一堆函数,然后我也确实这么做了,经过一堆调试(字符和数字之间转化容易忘记),…

跨平台表空间传输(摘自eygle《循序渐进Oracle》)
需要注意的是,在Oracle 10g之前,数据文件是不能够跨平台传输使用的,从Oracle 10g开始,Oracle支持跨平台的表空间传输,这极大地增强了数据迁移的便利性。 1. 字节顺序和平台 数据文件所以不能跨平台,主要是…

EditPlus集成Java编译和运行命令组建轻量级Java SE开发工具
http://www.gogogogo.me/development/EditPlus-Java.html转载于:https://www.cnblogs.com/svennee/p/4071712.html

单例测试模式中【饿汉式】与【懒汉式】的区别
package day25.thread;/** /*** author Mr Chen* create 2018-10-09 18:37* 单例测试模式:保证类在内存中只有一个对象*/ public class Dome01 {public static void main(String[] args){Singleton s1 Singleton.s; //成员变量被私有…

1078 Hashing
关键在于这句:Quadratic probing (with positive increments only) is used to solve the collisions.开始不懂二次探测,因此做不出来。所谓二次探测就是如果num%mSize被占坑了,就看看(num1*1)%mSize有没有被占,还是被占ÿ…

C# 多线程 参数传递
class ThreadDemo { private Thread[] threads; private int thrs 10;//线程数量 private ArrayList stringList; private event EventHandler OnNumberClear;//数据删除完引发的事件 public ThreadDemo(int number) …

Android 中自定义控件和属性(attr.xml,declare-styleable,TypedArray)的方法和使用
一、 在res/values 文件下定义一个attrs.xml 文件.代码如下: <?xml version"1.0" encoding"utf-8"?> <resources> <declare-styleable name"MyView"> <attr name"textColor" format"color…

排序学习之---快速排序
一、前言 快速排序是一种交换排序,它由C. A. R. Hoare在1962年提出。 二、算法思想 快速排序的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数。 然后再按此方法对这两部…

1059 Prime Factors
1. 第一次测试点三错误,由于1既不是质数也不是合数,因此对于1来说需要有一个特殊判断,输出:11,但是一开始多加了一个等号。 2. 本题需要数学基础好,两个重点: (1)会打印某个范围内的素数表 (…

适用于SQL Server生产环境DBA的七大技巧
摘自:http://database.ctocio.com.cn/452/8976452.shtml1、使用forfiles命令删除陈旧的数据库备份文件 从Windows Server 2003开始forfiles命令就是Windows的一个自带命令行工具,它主要用于对文件的批处理, 利用SQL Server代理作业࿰…

关于PCA算法的一点学习总结
本文出处:http://blog.csdn.net/xizhibei PCA,也就是PrincipalComponents Analysis,主成份分析,是个非常优秀的算法,依照书上的说法: 寻找最小均方意义下,最能代表原始数据的投影方法 然后自己…

1096 Consecutive Factors
1. 对于题目描述中 list the smallest sequence of the consecutive factors 正确理解是:如果有多组连续因子,输出开头因子最小的那个序列(一开始理解成输出数目最小的那个序列) 2. 想象一下这种情况,2*3*4*5 120,4*5*6 120&am…

百度DisConf分布式配置框架源码试读(一)HttpClient 长连接
Spring Cloud Config配置中心我在学习Spring Cloud Config配置中心时理解了它体系下的配置中心的强大。实现了配置的远程管理、微服务的配置更新。Spring Cloud Config配置中心体系还是有其不足的地方。虽然它实现了配置和服务的分离。但是做不到实时的更新。需要手动触发POST …

开篇第一题:经典中的经典!
开篇第一题:经典中的经典!——评《编程之美》原贴地址:http://www.douban.com/review/2130819/ 应该是差不多两个月前收到了这本书,一直到最近才抽出时间来看了下,这本书的开篇的第一题现在基本已经成了经典中的经典了…

(C++)高精度整数的存储、读入、比较和四则运算
目录 1. 存储 2. 读入 3. 比较大小 4. 加法 5. 减法 6. 高精度整数和低精度整数的乘法 7. 高精度整数除以低精度整数 高精度整数,又称大整数,其含义就是用基本数据类型无法存储其精度的整数。如:10进制下有着1000个数位的整数。 低精…

TP-link 设置MAC地址过滤
如果你想限制上网的人数,你可以在路由中设置MAC地址过滤,或IP地址过滤 以下以MAC地址过滤为例: http://192.168.1.1/ 输入用户名,密码登录 进入介面: “开启防火墙(防火墙的总开关)” 也要打上…

flask的客户端服务端
1.首先要进行后端与前端的连接有get 和post请求 get请求是直接在网页上打出已将定义好的网址 if __name__ __main__: app.run(host"localhost",port8800)host也可以写ip地址2.在进行交互前需要提前引入 flask 模块 pip3 install Flask详细代码 1 import json2 #…

1023 Have Fun with Numbers
考察大数乘法(整型是2)或者加法(两个相同的数字相加),然后将两个大数用到的0-9的个数比对。 进入比对前先判断长度是否相等,如不等,说明一定不是原序列。 一些需要注意的细节: 1. 字符串的字符转化为整数时不要忘记 减0 2. 封…

Oracle中Hint深入理解(原创)
http://czmmiao.iteye.com/blog/1478465 Hint概述 基于代价的优化器是很聪明的,在绝大多数情况下它会选择正确的优化器,减轻了DBA的负担。但有时它也聪明反被聪明误,选择了很差的执行计划,使某个语句的执行变得奇慢无比。 此时就…

css sprites之圆角
第一步:创建我们的 Sprite用PS等工具合成如图所示的图片(以一个像素的红线来区分)第二部分:编写HTML代码首先,我们会给容器 div 一个 .roundedBox类 :<div class"roundedBox"></div> 现在,我们必…

爬虫原理与数据抓取----- urllib2:URLError与HTTPError
urllib2 的异常错误处理 在我们用urlopen或opener.open方法发出一个请求时,如果urlopen或opener.open不能处理这个response,就产生错误。 这里主要说的是URLError和HTTPError,以及对它们的错误处理。 URLError URLError 产生的原因主要有&…

1024 Palindromic Number
1. 本题给的N的范围是10位以内的整数,但是注意了不知要要和反序列相加多少次,因此大数的int d[]的大小10是远远不够,100才全部AC。 2. 一开始不通过不知道是位数不够,以为是到确定步数停下来的代码写错了,其实通过两个…

HibernateTemplate 查询
Spring中常用的hql查询方法getHibernateTemplate()上 一、find(String queryString); 示例:this.getHibernateTemplate().find("from bean.User"); 返回所有User对象 二、find(String queryString , Object value); 示例:this.getH…

EMQ学习笔记---Clean Session和Retained Message
MQTT会话(Clean Session)MQTT客户端向服务器发起CONNECT请求时,可以通过’Clean Session’标志设置会话。‘Clean Session’设置为0,表示创建一个持久会话,在客户端断开连接时,会话仍然保持并保存离线消息,直到会话超时…

JPA相关--Annotation
1.自定义注解import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;Target(ElementType.METHOD) //指定可以用在什么地方,默认所有地方 Retention(…

(C++)变长数组vector的常见用法
目录 1. vector的定义 2. vector内的元素访问 3. vector常用函数 push_back(x) pop_back() size() clear() insert(it,x) erase(it)和erase(first,last) 4. vector常见用途 1.存储数据 2.用邻接表存储图 1. vector的定义 1.1 单独定义vector vector<typename&…

【kuangbin专题】计算几何_半平面交
1.poj3335 Rotating Scoreboard 传送:http://poj.org/problem?id3335 题意:就是有个球场,球场的形状是个凸多边形,然后观众是坐在多边形的边上的,问你是否在球场上有个地方可以放一个记分牌,然后所有的观众…
