1003 Emergency(Dijkstra,Bellman-Ford,SPFA三种解法)
目录
1. Dijkstra解法
2. Bellman-Ford解法
3. SPFA解法
4. Dijkstra解法AC代码
5. Bellman-Ford解法AC代码
6. SPFA解法AC代码
1. Dijkstra解法
这题不仅涉及到基础的解法,还涉及到第二标准(累计军队数量),以及还要记录最短路径条数。这些都是在绷紧路径的if语句中修改,我认为自己在这里的嵌套判断写法(先判断该结点是否已被访问过再进行下一步)比书上的复合条件句要清楚
//绷紧路径
for(int j=0;j<city[minC].nbr.size();j++){int nbr = city[minC].nbr[j].no;if(vis[nbr]==0){if(d[minC]+city[minC].nbr[j].dis<d[nbr]){n[nbr] = n[minC];d[nbr] = d[minC]+city[minC].nbr[j].dis;t[nbr] = t[minC] + city[nbr].teamN;}else if(d[minC]+city[minC].nbr[j].dis==d[nbr]){n[nbr] += n[minC];if(t[minC] + city[nbr].teamN > t[nbr])t[nbr] = t[minC] + city[nbr].teamN;}}
} 对于起点的初始化,有三个条件就要初始化三个
//将起点的距离设置为0
d[sCity] = 0;
//将起点的最短路径条数设置为1
n[sCity] = 1;
//将起点的军队数目设置为自身所有
t[sCity] = city[sCity].teamN;值得注意的是最短路径条数的更新,如果有优化方案,当前结点的最短路径数目应该赋值为前驱结点的最短路径数目而不是1,如果有同样优的方案,当前结点的最短路径数目应该增加前驱结点的最短路径数目而不是加1。
2. Bellman-Ford解法
BF算法可以判断有没有可达负环,但是在这题的背景下用不到。它主要分为紧绷部分和判断负环部分。同样棘手的是最短路径的条数怎么办,当遇到可以紧绷时,直接用前驱的路径条数更新后继节点的,这个和Dijkstra一样,但是当遇到同优策略时,就不一样了,起初我也不会,看了参考书明白。需要设置一个前趋结点表set<int> pre[maxn],如果遇到同优路径,先把当前前驱结点加入,然后把当前结点的最短路径数清零(非常容易忘),对前驱结点集合进行遍历,所有前驱结点的最短路径条数之和就是当前结点的最短路径条数。此外,遇到更优路径的时候,需要先把前驱结点集合清空,再插入当前前驱结点。
注意:初始化是否完备,根据题意逻辑处理是否正确,BF不需要vis[maxn]数组
int v = G[u][j].v;//v是u的邻接节点if(d[v]>d[u]+G[u][j].w){d[v] = d[u]+G[u][j].w;h[v] = h[u]+H[v];pre[v].clear();pre[v].insert(u);n[v] = n[u];}else if(d[v]==d[u]+G[u][j].w){pre[v].insert(u);n[v] = 0;for(set<int>::iterator it = pre[v].begin();it!=pre[v].end();it++){n[v] += n[*it];}if(h[v]<h[u]+H[v])h[v] = h[u]+H[v]; } 3. SPFA解法
这里用的是BFS版本的SPFA,利用的规律是“d[u]变,只有u的后继节点的最短路径才有可能改变”,所以在进行一次优化以后(不管是第一尺度还是第二尺度),才把当前优化过的结点放进队列中。至于数目的更新,由于这其实是改进的BF算法,和BF是一样的。
if(d[v]>d[u]+dis){d[v] = d[u]+dis;h[v] = h[u]+H[v];pre[v].clear();pre[v].insert(u);n[v] = n[u];if(inq[v]==false){Q.push(v);inq[v] = true;num[v] ++;if(num[v]>=vNum)return false;}
}else if(d[v]==d[u]+dis){pre[v].insert(u);n[v] = 0;for(set<int>::iterator it = pre[v].begin();it!=pre[v].end();it++){n[v]+=n[*it];}if(h[v]<h[u]+H[v])h[v] = h[u]+H[v];if(inq[v]==false){Q.push(v);inq[v] = true;num[v] ++;if(num[v]>=vNum)return false;}
}4. Dijkstra解法AC代码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;const int INF = 1000000000;//10的9次方
const int maxn = 510;
const double eps = 1e-3;struct Node{int no;int dis;Node(int _no,int _dis):no(_no),dis(_dis){}};struct City{vector<Node> nbr;int teamN;
}city[maxn];int cityN,roadN,sCity,dCity;bool vis[maxn] = {0};
int d[maxn];
int t[maxn] = {0};//数组t存放的是最短路径上累积的最大救援队数
int n[maxn] = {0};//n存放最短路径的数量void Dijkstra(){//填充最短距离路径数组(其他三个都初始化过了)fill(d,d+cityN,INF);//将起点的距离设置为0 d[sCity] = 0;//将起点的最短路径条数设置为1n[sCity] = 1;//将起点的军队数目设置为自身所有t[sCity] = city[sCity].teamN; for(int i=0;i<cityN;i++){//每一次访问一个结点 //找到距离当前数组距离最小的数组int minD = INF,minC = -1;//最短距离和对应城市编号for(int j=0;j<cityN;j++){if(d[j]<minD&&vis[j]==0){minD = d[j];minC = j;} } if(minC==-1)return;//说明所有结点都加入了S else vis[minC] = 1;//绷紧路径for(int j=0;j<city[minC].nbr.size();j++){int nbr = city[minC].nbr[j].no;if(vis[nbr]==0){if(d[minC]+city[minC].nbr[j].dis<d[nbr]){n[nbr] = n[minC];d[nbr] = d[minC]+city[minC].nbr[j].dis;t[nbr] = t[minC] + city[nbr].teamN;}else if(d[minC]+city[minC].nbr[j].dis==d[nbr]){n[nbr] += n[minC];if(t[minC] + city[nbr].teamN > t[nbr])t[nbr] = t[minC] + city[nbr].teamN;}}} }
}int main(){scanf("%d %d %d %d",&cityN,&roadN,&sCity,&dCity);//读入每个城市救援队的数量 for(int i=0;i<cityN;i++){scanf("%d",&city[i].teamN);}//读入每一条路的长度for(int i=0;i<roadN;i++){int c1,c2,len;scanf("%d %d %d",&c1,&c2,&len);Node* n1 = new Node(c1,len);city[c2].nbr.push_back(*n1);Node* n2 = new Node(c2,len);city[c1].nbr.push_back(*n2);}//调用Dijkstra算法Dijkstra(); printf("%d %d\n",n[dCity],t[dCity]); return 0;
}5. Bellman-Ford解法AC代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<map>
#include<set>
#include<cstring>using namespace std;const int maxn = 510;
const int SUP = 2000000000;struct Node{int v,w;Node(int _v,int _w):v(_v),w(_w){}
};vector<Node> G[maxn];int H[maxn];//各个城市固有帮手数量
int d[maxn];
int h[maxn] = {0};//从源点到某地最多的帮手数量
int n[maxn] = {0};//到达某地的最短路径数 int vNum;set<int> pre[maxn];bool Bellman(int so){fill(d,d+vNum,SUP);d[so] = 0;h[so] = H[so];n[so] = 1;for(int i=0;i<vNum-1;i++){for(int u=0;u<vNum;u++){for(int j=0;j<G[u].size();j++){int v = G[u][j].v;//v是u的邻接节点if(d[v]>d[u]+G[u][j].w){d[v] = d[u]+G[u][j].w;h[v] = h[u]+H[v];pre[v].clear();pre[v].insert(u);n[v] = n[u];}else if(d[v]==d[u]+G[u][j].w){pre[v].insert(u);n[v] = 0;for(set<int>::iterator it = pre[v].begin();it!=pre[v].end();it++){n[v] += n[*it];}if(h[v]<h[u]+H[v])h[v] = h[u]+H[v]; } }}}for(int u=0;u<vNum;u++){for(int j=0;j<G[u].size();j++){int v = G[u][j].v;if(d[v]>d[u]+G[u][j].w)return false;}}return true;
}int main(){int eNum,so,de;scanf("%d %d %d %d",&vNum,&eNum,&so,&de); for(int i=0;i<vNum;i++){scanf("%d",&H[i]);}int v1,v2,w;for(int i=0;i<eNum;i++){scanf("%d %d %d",&v1,&v2,&w);Node node = Node(v2,w);G[v1].push_back(node);node = Node(v1,w);G[v2].push_back(node);}Bellman(so);printf("%d %d",n[de],h[de]);return 0;
}6. SPFA解法AC代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
#include<vector>
#include<string>
#include<queue>
#include<map>
#include<set>
#include<cstring>using namespace std;const int maxn = 510;
const int SUP = 2000000000;struct Node{int v,w;Node(int _v,int _w):v(_v),w(_w){}
};vector<Node> G[maxn];int H[maxn];//各个城市固有帮手数量
int d[maxn];
int h[maxn] = {0};//从源点到某地最多的帮手数量
int n[maxn] = {0};//到达某地的最短路径数
int num[maxn] = {0};//各个点入队次数 int vNum;set<int> pre[maxn];bool SPFA(int so){fill(d,d+vNum,SUP);d[so] = 0;n[so] = 1;h[so] = H[so];bool inq[maxn] = {0};queue<int> Q;Q.push(so);inq[so] = true;while(!Q.empty()){int u = Q.front();Q.pop();inq[u] = false;for(int i=0;i<G[u].size();i++){int v = G[u][i].v;int dis = G[u][i].w;if(d[v]>d[u]+dis){d[v] = d[u]+dis;h[v] = h[u]+H[v];pre[v].clear();pre[v].insert(u);n[v] = n[u];if(inq[v]==false){Q.push(v);inq[v] = true;num[v] ++;if(num[v]>=vNum)return false;}}else if(d[v]==d[u]+dis){pre[v].insert(u);n[v] = 0;for(set<int>::iterator it = pre[v].begin();it!=pre[v].end();it++){n[v]+=n[*it];}if(h[v]<h[u]+H[v])h[v] = h[u]+H[v];if(inq[v]==false){Q.push(v);inq[v] = true;num[v] ++;if(num[v]>=vNum)return false;}}}}return true;
}int main(){int eNum,so,de;scanf("%d %d %d %d",&vNum,&eNum,&so,&de); for(int i=0;i<vNum;i++){scanf("%d",&H[i]);}int v1,v2,w;for(int i=0;i<eNum;i++){scanf("%d %d %d",&v1,&v2,&w);Node node = Node(v2,w);G[v1].push_back(node);node = Node(v1,w);G[v2].push_back(node);}SPFA(so);printf("%d %d",n[de],h[de]);return 0;
}相关文章:

存储过程4-前台
代码 ALTERproc[dbo].[P_CheckCode](retintoutput,nIdint,tagnvarchar(50),cCodenvarchar(50),nHotelIdint)asbeginifUpper(tag)B_AREAbeginifexists(select1fromB_Area wherecCodecCodeandnHotelIdnHotelIdandnId<>nId) setret1elsesetret-1endelseifUpper(t…

安卓学习-其他-文件读写
在android中的文件放在不同位置,它们的读取方式也有一些不同。 本文对android中对资源文件的读取、数据区文件的读取、SD卡文件的读取及RandomAccessFile的方式和方法进行了整理。供参考。 一、资源文件的读取: 1) 从resource的raw中读取文件数据&#x…

X5同层播放器应用实践
移动端浏览器中的video元素是比较特别的,早期无论是在iOS还是Android的浏览器中,它都位于页面的最顶层,无法被遮挡。后来,这个问题在iOS下得到了解决。但是对Android的大部分浏览器来说,问题仍然存在。X5是腾讯基于Web…

1007 Maximum Subsequence Sum(两种思路)
1.解法1 思路 对于动态规划来说,最关键的就是找到状态转移方程,本题设置一个前向数组,元素predp[i]表示的是以元素i结尾的连续数列和的最大值,转移方程是predp[i] max(predp[i-1]a[i],a[i])。要做的事就是完成这个dp数组&#x…
C#学习-EF在三层中使用
1.搭建普通三层 DAL层,BLL层,Model层,Web层; DAL层引用Model层 BLL层引用DAL层和Model层 Web层引用BLL层和Model层 2.实现EF三层的搭建(添加引用,修改配置信息) 2.1添加EF对象 在Model中添加一个…

各大IT公司笔试真题汇总开发人员一定要加入收藏夹的网站(收藏)
巨人网络java笔试基础题分享 http://www.coderarea.net/bbs/read.php?tid834 百度笔试题 http://www.coderarea.net/bbs/read.php?tid811 百度2010校招运维部门笔试 http://www.coderarea.net/bbs/read.php?tid779 百度2010年校园招聘软件测试笔试题 http://www.coderarea.n…

Python编写Hive UDF
2019独角兽企业重金招聘Python工程师标准>>> 1. 目的 从string类型的字段中解析并汇总每种category类型的总amount 2. 素材 表名:test_table order_no hotel_seq discount_detail D8662EF4E 10212527 NULL 45C024849 …

1045 Favorite Color Stripe(LIS解法)
解题思路 本题属于Longest Increasing Sequence最长不下降子序列,但是要注意,LIS当中不会有无效的元素,而本题是有的,所以先要把无效元素过滤掉,才能转化成为LIS问题。 这里用到了hashTable(用map更慢),初…

5.8fork父子进程
实验4-2:fork父子进程 实验目的: 理解fork创建子进程的本质 实验要求: 1、按如下要求编写程序: (1)、打开一个有内容的文件; (2)、调用fork创建子进程; (3)、读文件…

word表格自动编号
选中全部内容--右键--项目符号和编号--自定义--编号样式--选01,02样式.则生成所有编号选中第二批编号,--重新编号,就又从01开始了转载于:https://www.cnblogs.com/wzshhynk/archive/2009/12/30/1635805.html

Vue API(directives) 自定义指令
前言:除了vue的内置指令以外,我们可以定义自定义指令。内置指令表相见:https://www.cnblogs.com/ilovexiaoming/p/6840383.html 我们定义一个最简单的 <script> export default {name: App,data(){return{yanse:red}},// 所有自定义指令…

1045 Favorite Color Stripe(LCS解法) 需再理解
解题思路 使用LCS方法解这一题,首先要把现有的颜色和Eva的颜色看成即将取材的序列s和e。 而且注意2个序列都要从1开始读入,因为递归边界(待后叙)。 dp[i][j]代表的是e[1]-e[i]和s[1]-s[j]的范围内,公共子序列的长度…

C++ primer第五版随笔--2015年1月6日
记录自己看这本书时的一些内容。 一、引用(reference) 引用为对象起了另外一个名字。例如: int ival1024; int &relVal1ival;//对,注意尽量不要用这方式:int& relvalival; int &rel…
Python性能分析指南——中
程序使用了多少内存?现在我们对计时有了较好的理解,那么让我们继续弄清楚程序使用了多少内存。我们很幸运,Fabian Pedregosa模仿Robert Kern的line_profiler实现了一个不错的内存分析器。首先使用pip安装:这里建议安装psutil包,因…

1040 Longest Symmetric String 需再做
解题思路 本题属于最长回文子串专题下。与之前的LIS和LCS的动规有两个较大的不同 1. 虽然最后也是要求长度,但是长度信息不再蕴含在dp数组当中,dp[i][j]表示的仅仅是从s[i]起s[j]止这一段是否是回文,所以为了提醒自己,我设置成了…

回顾2009,展望2010。
回顾2009,展望2010。 2009即将过去,总结2009年,计划2010年。 2009年12月31日。转载于:https://www.cnblogs.com/finehappy/archive/2009/12/31/1654975.html

Linux Mint 19 安装Gnome Boxes 新建失败
之前在Ubuntu论坛提出,一直没有解决.http://forum.ubuntu.org.cn/viewtopic.php?f65&t488821 后参照: https://askubuntu.com/questions/836703/ ... sue/836715对方报错: (gnome-boxes:15984): Boxes-WARNING **: wizard.vala:463: Fai…

1057 Stack
目录 解题思路 AC代码 解题思路 虽然题目的名字是栈,但是这题和栈的关系很小,甚至我都没有用到stack这个数据结构,而是用vector<int>的pop_back()来模拟栈的弹出。 主要考察的是:在线查询,也就是查询过程中…
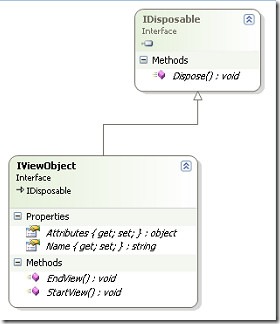
【译】使用自定义ViewHelper来简化Asp.net MVC view的开发------part1
从开发者的角度来看,创建Asp.net MVC的View是一件很爽的事,因为你可以精确控制最终生成的HTML。具有讽刺意味的是不得不写出每一行HTML代码同时也是Asp.net MVC的View中让人不爽的地方。让我用我的一个经历来告诉我创建ASP.Net MVC view Helpers背后灵感…

看书挑剔,只看经典
如何选择经典,可以到网上做做功课,看看评价,综合分析一下。书籍是我们知识的主要来源。在选择书籍的时候做足功课是对我们自己时间的负责;这和在超市里买东西时对比各个品牌是一个道理;只不过奇怪的是,我很…
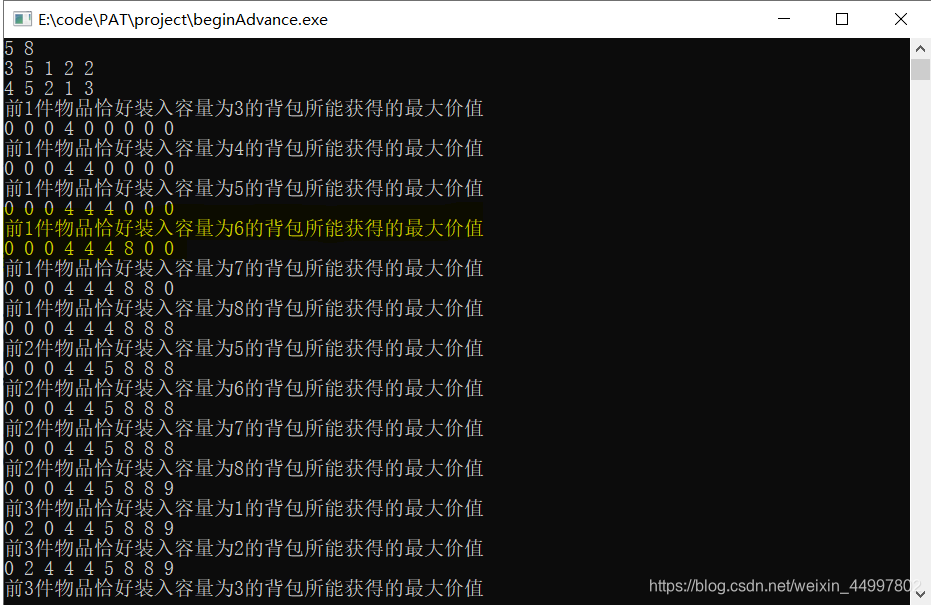
0-1背包使用一维dp数组时为何v要从大到小枚举
样例数据 5 8 3 5 1 2 2 4 5 2 1 3 如若不然,也就是让v按照从小到大的顺序枚举,就会出现 注意高亮的那一行,第一件物品的重量只有3,怎么会得到6呢? 代码如下 #include<cstdio> #include<cmath> #inclu…

异步编程模型--使用 IAsyncResult 对象
先推荐阅读下面的资料:MSDN:异步编程设计模式IBM developerworks: 使用异步 I/O 大大提高应用程序的性能参考博文:1、正确使用异步操作 2、Lab:体会ASP.NET异步处理请求的效果 3、WCF中的异步调用 4、WCF从理论到实践(…

对XX证券报关于物联网操作系统的几个问题的答复
XX证券报提问了几个关于物联网和物联网操作系统的问题,个人表达了一些粗陋的观点,在这里发表出来,与行业朋友交流和探讨。物联网行业最需要解决的问题是什么?虽然物联网这个行业被炒得比较热,但是截至目前,…

Java基础 - 面向对象 - 构造方法
在类中除了成员方法之外,还存在一种特殊类型的方法,那就是构造方法。构造方法是一个与类同名的方法,对象的创建就是通过构造方法完成的。每当类实例化一个对象时,类都会自动调用构造方法。 构造方法的特点: 构造方法没…

1105 Spiral Matrix 给定数组向螺旋矩阵中填入数据
两个测试用例超时,可直接跳转到 目录 超时点1 超时点2 要做的事情是,将数组按照非升序/降序,顺时针从外围到内部一圈一圈地把数据填到矩阵中,并打印出来。也就是将数组排好序后,将矩阵的坐标和数组…

一晚上就能让你小腹变小的方法 - 健康程序员,至尚生活!
仅一晚上针对小腹的锻炼就会让它明显收紧,很不可思议吧?但它确实发生了。形体教练向我们推荐:做30次转身运动(双手抱在脑后站立,迅速分别向左右两侧依次扭转上肢,注意不要以膝盖为轴,使运动轴心保持在骨盆以…
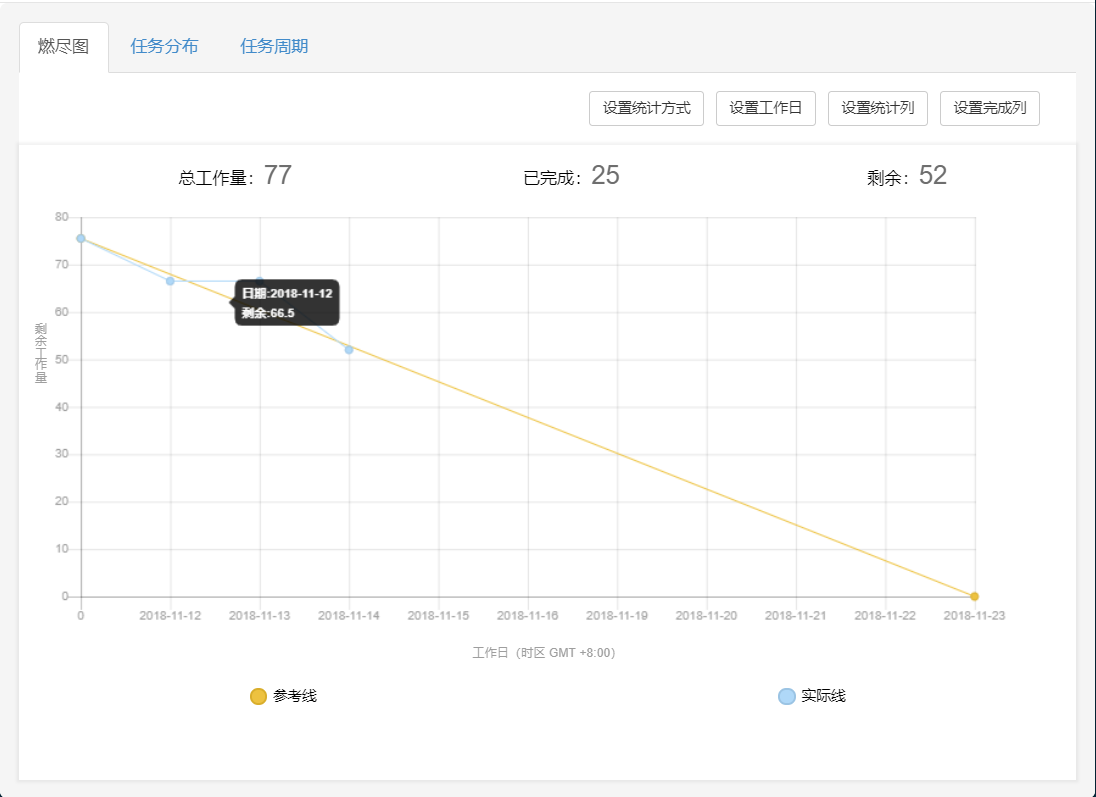
Alpha 冲刺 (2/10)
前言 队名:拖鞋旅游队组长博客:https://www.cnblogs.com/Sulumer/p/9960487.html作业博客:https://edu.cnblogs.com/campus/fzu/Grade2016SE/homework/2365组内情况 燃尽图任务分布github签入记录苏路明(组长)过去两天…

互联网对erp行业到底有什么影响
1 财务管理的影响 总账、 应收应付、资金计划,支付管理。 生产计划的影响。 重大的疑惑。 转载于:https://www.cnblogs.com/sdgxbooy/p/8892655.html

PAT甲级排队问题合集 (持续更新中)
已加入的习题 A1014,A1017 问题1和2共性 1. 都是排队问题 2. 都有一条黄线 3. 都需要找到最先离开人的队伍 4. 都有着服务时间段限制(迟于某个时间点来不予受理) 问题1:1014 Waiting in Line 问题链接:1014 Waiting in Line 这一题,…

第三章:创建用户界面组件--可视化组件(一)
1.可视化组件 1.1关于可视化组件 可视化组件的特征包括:size(大小)、事件、样式、皮肤、行为。 行为:当组件被触发时,视觉,音乐效果的变化。 1.1 .1Spark and Halo 组件 Spark是flex 4中新加的组件。halo仍旧继承了以…
