1007 Maximum Subsequence Sum(两种思路)
1.解法1 思路
对于动态规划来说,最关键的就是找到状态转移方程,本题设置一个前向数组,元素predp[i]表示的是以元素i结尾的连续数列和的最大值,转移方程是predp[i] = max(predp[i-1]+a[i],a[i])。要做的事就是完成这个dp数组,然后找到最大的dp[i]。
根据i可以直接得到结束元素,那开始元素怎么办呢?我们还需要另开一个计数数组n[maxn],记录下数目。
注意:要获得坐标尽可能小的起始元素和终止元素,体现在代码的两个地方
1是:哪怕前面的元素加上是鸡肋,为了起始坐标小,也把它加上
for(int i=1;i<n;i++){if(predp[i-1]+a[i]>=a[i]){num[i] = num[i-1]+1;predp[i] = predp[i-1]+a[i];}else{num[i] = 1;predp[i] = a[i]; }
}2是:在挑选最大dp[i]的时候,哪怕后面出现了同样大的,也不要
int preI,preMax = -1;
for(int i=0;i<n;i++){if(predp[i]>preMax){preMax = predp[i];preI = i;}
}2.解法2 思路
设置一前一后两个状态转移方程,并且由于最后希望起始坐标和终止坐标都尽可能小,所以对于前向数组找最大下标的时候,必须是大于,才能允许坐标被增大,对于反向数组找最大下标的时候,满足大于等于,就允许坐标被减小。原理是:正向得到最大值的数列,和反向得到最大值的数列是同一个。
3.解法1 AC代码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;const int INF = 1000000000;//10的9次方
const int maxn = 100010;
const double eps = 1e-3;int n;
int a[maxn];
int predp[maxn];
int num[maxn];
bool isSpe = true;int main(){scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);if(a[i]>=0)isSpe = false;//说明不是特例 }if(isSpe){printf("0 %d %d\n",a[0],a[n-1]);return 0;}//解决predp[0]和num[0]predp[0] = a[0];num[0] = 1;for(int i=1;i<n;i++){if(predp[i-1]+a[i]>=a[i]){num[i] = num[i-1]+1;predp[i] = predp[i-1]+a[i];}else{num[i] = 1;predp[i] = a[i]; }}int preI,preMax = -1;for(int i=0;i<n;i++){if(predp[i]>preMax){preMax = predp[i];preI = i;}}printf("%d %d %d\n",preMax,a[preI-num[preI]+1],a[preI]); return 0;
}4.解法2 非满分(22/25)代码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<bits/stdc++.h>
using namespace std;const int INF = 1000000000;//10的9次方
const int maxn = 100010;
const double eps = 1e-3;int n;
int a[maxn];
int predp[maxn];
int postdp[maxn];
bool isSpe = true;int main(){scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);if(a[i]>=0)isSpe = false;//说明不是特例 }if(isSpe){printf("0 %d %d\n",a[0],a[n-1]);return 0;}predp[0] = max(0,a[0]);for(int i=1;i<n;i++){predp[i] = max(predp[i-1]+a[i],a[i]);}int preI,preMax = -1;for(int i=0;i<n;i++){if(predp[i]>preMax){preMax = predp[i];preI = i;}}postdp[n-1] = max(0,a[n-1]);for(int i=n-2;i>=0;i--){postdp[i] = max(postdp[i+1]+a[i],a[i]);}int postI,postMax = -1;for(int i=n-1;i>=0;i--){if(postdp[i]>=postMax){postMax = postdp[i];postI = i;}}printf("%d %d %d\n",postMax,a[postI],a[preI]); return 0;
}相关文章:
C#学习-EF在三层中使用
1.搭建普通三层 DAL层,BLL层,Model层,Web层; DAL层引用Model层 BLL层引用DAL层和Model层 Web层引用BLL层和Model层 2.实现EF三层的搭建(添加引用,修改配置信息) 2.1添加EF对象 在Model中添加一个…

各大IT公司笔试真题汇总开发人员一定要加入收藏夹的网站(收藏)
巨人网络java笔试基础题分享 http://www.coderarea.net/bbs/read.php?tid834 百度笔试题 http://www.coderarea.net/bbs/read.php?tid811 百度2010校招运维部门笔试 http://www.coderarea.net/bbs/read.php?tid779 百度2010年校园招聘软件测试笔试题 http://www.coderarea.n…

Python编写Hive UDF
2019独角兽企业重金招聘Python工程师标准>>> 1. 目的 从string类型的字段中解析并汇总每种category类型的总amount 2. 素材 表名:test_table order_no hotel_seq discount_detail D8662EF4E 10212527 NULL 45C024849 …

1045 Favorite Color Stripe(LIS解法)
解题思路 本题属于Longest Increasing Sequence最长不下降子序列,但是要注意,LIS当中不会有无效的元素,而本题是有的,所以先要把无效元素过滤掉,才能转化成为LIS问题。 这里用到了hashTable(用map更慢),初…

5.8fork父子进程
实验4-2:fork父子进程 实验目的: 理解fork创建子进程的本质 实验要求: 1、按如下要求编写程序: (1)、打开一个有内容的文件; (2)、调用fork创建子进程; (3)、读文件…

word表格自动编号
选中全部内容--右键--项目符号和编号--自定义--编号样式--选01,02样式.则生成所有编号选中第二批编号,--重新编号,就又从01开始了转载于:https://www.cnblogs.com/wzshhynk/archive/2009/12/30/1635805.html

Vue API(directives) 自定义指令
前言:除了vue的内置指令以外,我们可以定义自定义指令。内置指令表相见:https://www.cnblogs.com/ilovexiaoming/p/6840383.html 我们定义一个最简单的 <script> export default {name: App,data(){return{yanse:red}},// 所有自定义指令…

1045 Favorite Color Stripe(LCS解法) 需再理解
解题思路 使用LCS方法解这一题,首先要把现有的颜色和Eva的颜色看成即将取材的序列s和e。 而且注意2个序列都要从1开始读入,因为递归边界(待后叙)。 dp[i][j]代表的是e[1]-e[i]和s[1]-s[j]的范围内,公共子序列的长度…

C++ primer第五版随笔--2015年1月6日
记录自己看这本书时的一些内容。 一、引用(reference) 引用为对象起了另外一个名字。例如: int ival1024; int &relVal1ival;//对,注意尽量不要用这方式:int& relvalival; int &rel…
Python性能分析指南——中
程序使用了多少内存?现在我们对计时有了较好的理解,那么让我们继续弄清楚程序使用了多少内存。我们很幸运,Fabian Pedregosa模仿Robert Kern的line_profiler实现了一个不错的内存分析器。首先使用pip安装:这里建议安装psutil包,因…

1040 Longest Symmetric String 需再做
解题思路 本题属于最长回文子串专题下。与之前的LIS和LCS的动规有两个较大的不同 1. 虽然最后也是要求长度,但是长度信息不再蕴含在dp数组当中,dp[i][j]表示的仅仅是从s[i]起s[j]止这一段是否是回文,所以为了提醒自己,我设置成了…

回顾2009,展望2010。
回顾2009,展望2010。 2009即将过去,总结2009年,计划2010年。 2009年12月31日。转载于:https://www.cnblogs.com/finehappy/archive/2009/12/31/1654975.html

Linux Mint 19 安装Gnome Boxes 新建失败
之前在Ubuntu论坛提出,一直没有解决.http://forum.ubuntu.org.cn/viewtopic.php?f65&t488821 后参照: https://askubuntu.com/questions/836703/ ... sue/836715对方报错: (gnome-boxes:15984): Boxes-WARNING **: wizard.vala:463: Fai…

1057 Stack
目录 解题思路 AC代码 解题思路 虽然题目的名字是栈,但是这题和栈的关系很小,甚至我都没有用到stack这个数据结构,而是用vector<int>的pop_back()来模拟栈的弹出。 主要考察的是:在线查询,也就是查询过程中…
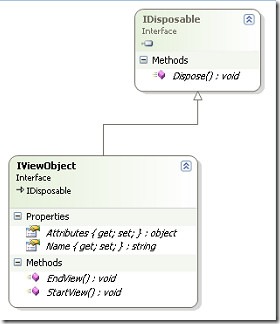
【译】使用自定义ViewHelper来简化Asp.net MVC view的开发------part1
从开发者的角度来看,创建Asp.net MVC的View是一件很爽的事,因为你可以精确控制最终生成的HTML。具有讽刺意味的是不得不写出每一行HTML代码同时也是Asp.net MVC的View中让人不爽的地方。让我用我的一个经历来告诉我创建ASP.Net MVC view Helpers背后灵感…

看书挑剔,只看经典
如何选择经典,可以到网上做做功课,看看评价,综合分析一下。书籍是我们知识的主要来源。在选择书籍的时候做足功课是对我们自己时间的负责;这和在超市里买东西时对比各个品牌是一个道理;只不过奇怪的是,我很…
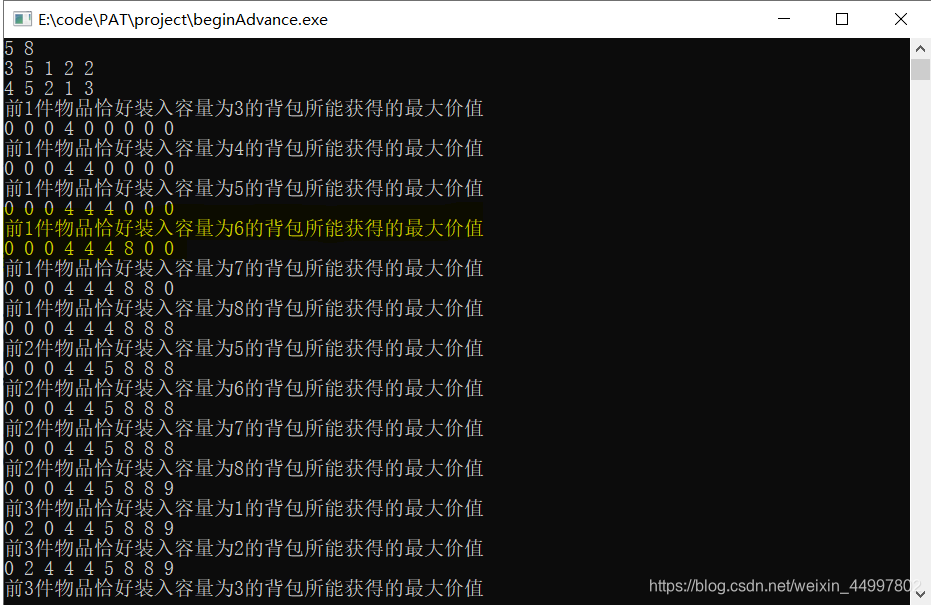
0-1背包使用一维dp数组时为何v要从大到小枚举
样例数据 5 8 3 5 1 2 2 4 5 2 1 3 如若不然,也就是让v按照从小到大的顺序枚举,就会出现 注意高亮的那一行,第一件物品的重量只有3,怎么会得到6呢? 代码如下 #include<cstdio> #include<cmath> #inclu…

异步编程模型--使用 IAsyncResult 对象
先推荐阅读下面的资料:MSDN:异步编程设计模式IBM developerworks: 使用异步 I/O 大大提高应用程序的性能参考博文:1、正确使用异步操作 2、Lab:体会ASP.NET异步处理请求的效果 3、WCF中的异步调用 4、WCF从理论到实践(…

对XX证券报关于物联网操作系统的几个问题的答复
XX证券报提问了几个关于物联网和物联网操作系统的问题,个人表达了一些粗陋的观点,在这里发表出来,与行业朋友交流和探讨。物联网行业最需要解决的问题是什么?虽然物联网这个行业被炒得比较热,但是截至目前,…

Java基础 - 面向对象 - 构造方法
在类中除了成员方法之外,还存在一种特殊类型的方法,那就是构造方法。构造方法是一个与类同名的方法,对象的创建就是通过构造方法完成的。每当类实例化一个对象时,类都会自动调用构造方法。 构造方法的特点: 构造方法没…

1105 Spiral Matrix 给定数组向螺旋矩阵中填入数据
两个测试用例超时,可直接跳转到 目录 超时点1 超时点2 要做的事情是,将数组按照非升序/降序,顺时针从外围到内部一圈一圈地把数据填到矩阵中,并打印出来。也就是将数组排好序后,将矩阵的坐标和数组…

一晚上就能让你小腹变小的方法 - 健康程序员,至尚生活!
仅一晚上针对小腹的锻炼就会让它明显收紧,很不可思议吧?但它确实发生了。形体教练向我们推荐:做30次转身运动(双手抱在脑后站立,迅速分别向左右两侧依次扭转上肢,注意不要以膝盖为轴,使运动轴心保持在骨盆以…
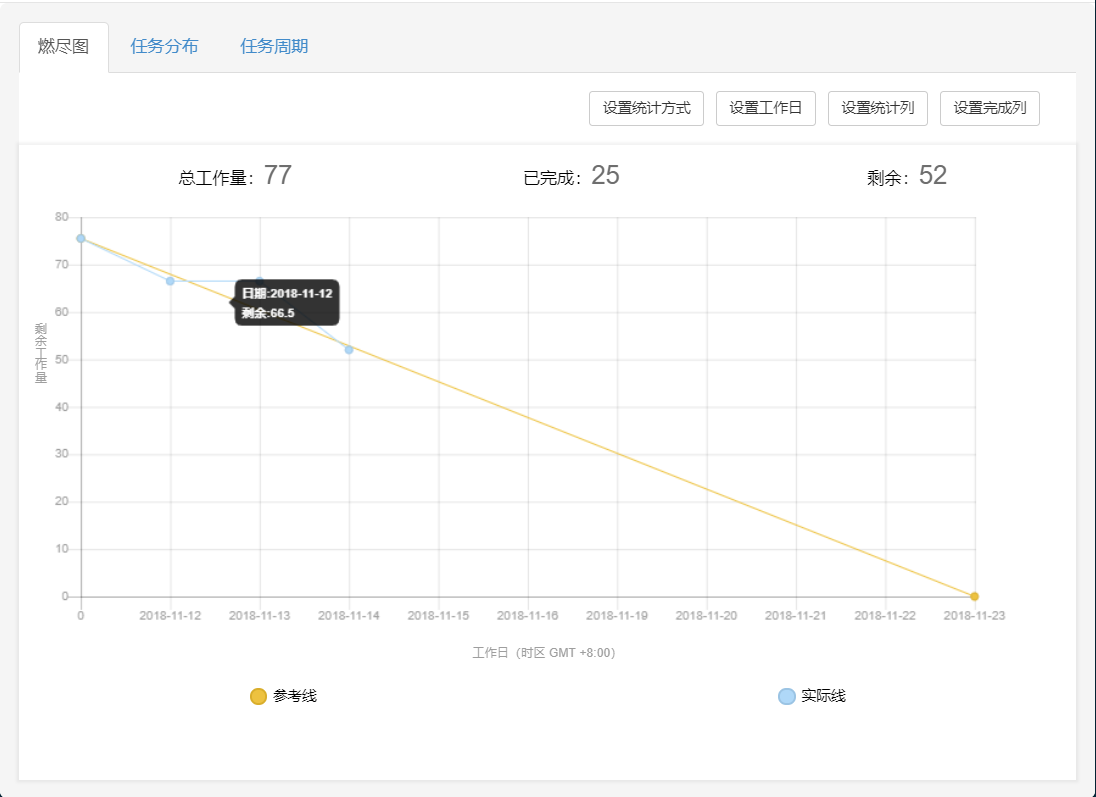
Alpha 冲刺 (2/10)
前言 队名:拖鞋旅游队组长博客:https://www.cnblogs.com/Sulumer/p/9960487.html作业博客:https://edu.cnblogs.com/campus/fzu/Grade2016SE/homework/2365组内情况 燃尽图任务分布github签入记录苏路明(组长)过去两天…

互联网对erp行业到底有什么影响
1 财务管理的影响 总账、 应收应付、资金计划,支付管理。 生产计划的影响。 重大的疑惑。 转载于:https://www.cnblogs.com/sdgxbooy/p/8892655.html

PAT甲级排队问题合集 (持续更新中)
已加入的习题 A1014,A1017 问题1和2共性 1. 都是排队问题 2. 都有一条黄线 3. 都需要找到最先离开人的队伍 4. 都有着服务时间段限制(迟于某个时间点来不予受理) 问题1:1014 Waiting in Line 问题链接:1014 Waiting in Line 这一题,…

第三章:创建用户界面组件--可视化组件(一)
1.可视化组件 1.1关于可视化组件 可视化组件的特征包括:size(大小)、事件、样式、皮肤、行为。 行为:当组件被触发时,视觉,音乐效果的变化。 1.1 .1Spark and Halo 组件 Spark是flex 4中新加的组件。halo仍旧继承了以…

Rust 1.30带来更多元编程支持,并改进了模块系统
Rust的最新版本1.30扩展了过程宏,允许它们定义新的属性和类似于函数的宏。此外,它简化了Rust模块系统,使其更加一致、直观。 Rust 1.30引入了两种新类型的过程宏,“类属性的过程宏”和“类函数的过程宏”。过程宏是Rust元编程的基…

两种最大堆建堆方式
都是用完全二叉树的静态存储方式,下标从1开始。 No.1 先按照数组的次序填入完全二叉树,再从倒数第一个非叶子节点开始,一个个地看是不是要向下调整,一直下调到不能再调。 void downAdjust(int low,int high){int i low;int j …

汉字验证码和算式验证码
大家知道简单数字或者字母验证码很容易被破解,但是算式验证码或者中文汉字验证码不容易被破解, 所以建议大家在使用验证码的时候,尽量用算式验证码或者中文汉字验证码。 下面是我写的两种验证码代码,有用到的朋友可以参考下&#…

自定义Linq的Distinct
代码 1 usingSystem;2 usingSystem.Collections.Generic;3 usingSystem.ComponentModel;4 usingSystem.Data;5 usingSystem.Drawing;6 usingSystem.Linq;7 usingSystem.Text;8 usingSystem.Windows.Forms;9 10 namespaceLinqTest11 {12 publicpartialclassForm1 : Form13 {14 p…
