机器学习01-定义、线性回归、梯度下降
目录
一、定义 What is Machine Learning
二、建模 Model Representation
三、一元线性回归 Linear Regression with One Variable
3.1 一元线性归回的符号约定 Notation
3.2 一元线性回归 Linear Regression with One Variable
3.3 代价函数 Cost Function
3.4 梯度下降概述 Gradient Descent Outline
3.5 梯度下降算法 Gradient Descent Alg
3.5.1 同步更新参数 Simultaneously Update
3.5.2 收敛 Convergence
3.5.3 学习率的取值 evaluate alpha
3.5.4 梯度下降更新参数公式
四、多元线性回归 Multiple Features and Gradient Descent
4.1 多元线性归回的符号约定 Notation
4.2 多元线性回归 Linear Regression with Multiple Variables
4.3 估值、代价函数、梯度下降
4.4 多元线性回归的矩阵描述
4.5 平均值归一化 Mean Normalization
4.6 多项式拟合 Polynomial Regression
4.7 过拟合Overfit与欠拟合Underfit
4.8 一般等式、梯度下降和一般等式的比较
复习Andrew Ng的课程Machine Learning,总结线性回归、梯度下降笔记一篇,涵盖课程week1、week2。
一、定义 What is Machine Learning
有两种业界比较认可的对机器学习的定义。
一种是Aithur Samuel在1959年给出的定义。机器学习:不需要明确编程就能使计算机具有学习能力的研究领域。
另一种是Tom Mitchell在1998年给出的定义。适定学习问题:如果一个计算机程序在任务T上的性能(以P衡量性能)随着经验E的提高而提高,那么它就被称为从经验E对某些任务T和性能度量P的学习。(拉倒吧,还是看英文原文吧!)
Machine Learning Definition
-Aithur Samuel 1959. Machine Learning: Field of study that gives computer the ability to learn without being explicitly programmed.
-Tom Mitchell 1998. Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and performance measure P, if its performance on T, as measured by P, improves with experience E.
二、建模 Model Representation
机器学习分很多种类
- Supervised Learning 有监督的学习
- Unsupervised Learning 无监督的学习
- Reinforcement learning 强化学习
- Recommender System 推荐系统
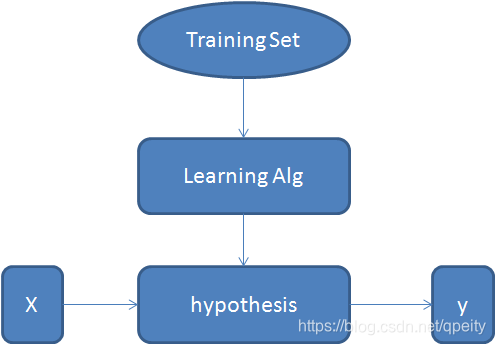
但是他们的建模几乎是一样的。都是通过在训练集(Training Set)上运行学习算法(Learning Alg)得到估值函数(hypothesis),这个假设函数可以对输入的特征X进行预测(估计 estimated value),输出y。
三、一元线性回归 Linear Regression with One Variable
3.1 一元线性归回的符号约定 Notation
约定一元线性回归问题中的符号定义。
训练集的大小。
输入变量,也就是特征。
输出变量,也就是估值。
一个训练用例。
训练集中的第i个用例。
3.2 一元线性回归 Linear Regression with One Variable
一元线性回归,Linear Regression with One Variable也叫做Univariate Linear Regression。其输入特征是一维的,输出值也是一维的。估值为 。一元线性回归的思想是,选择合适的
和
使
对训练集
上的
接近
。

Idea: Choose
so that
is close to
for our training example
.
minimize
3.3 代价函数 Cost Function
Cost Function Definition is square error function. 代价函数是平方误差函数。这个函数用来衡量估值与真实值之间的偏差。
代价函数是
其中 。使
最小的
和
值确定
。 公式里面为了表示“平均”,所以除以
,但为什么不简单的就写个
而是
呢?因为后面求导数的时候,平方的求导会把这个2抵消掉,这样导数式的样子就和逻辑回归问题的导数式子形式上统一了。
注意:
是关于
的函数,
和
是参数。也就是说求取导数的时候,变量是
。
是关于
的函数,
是参数。
3.4 梯度下降概述 Gradient Descent Outline
Have some function , Want
Outline:
- Start with some
- Keep changing
to reduce
until we hopefully end up at a minimum.
梯度下降的思想就是,我们先假定有
有某个值,通过改变
的值使
减小,直至得到最小值。
3.5 梯度下降算法 Gradient Descent Alg
3.5.1 同步更新参数 Simultaneously Update 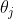
重复进行
,
其中是学习率(learning rate),必大于0。
注意,这种更新是各个维度上的同步更新,也就是说更新过程是这样的
3.5.2 收敛 Convergence
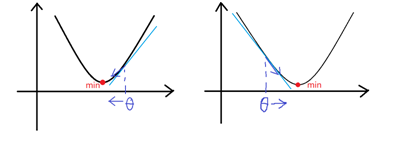
对于一元线性回归,代价函数的几何形状是个碗状曲面,因此代价函数一定收敛。根据上面同步更新的公式,我们分两种情况讨论,示意图如下。
当时,
减小,趋向于收敛;
当时,
增大,也趋向于收敛;
3.5.3 学习率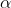 的取值 evaluate alpha
的取值 evaluate alpha
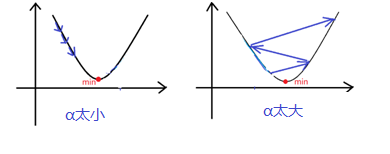
这个过程要注意学习率的取值应适中。如果
太小,收敛速率低,学习缓慢。如果
太大,可能跳过minimum不能收敛,甚至发散。示意图如下。
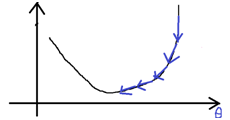
根据同步更新参数公式,,随着接近minimum,
逐渐减小。在接近minimum时,梯度下降自动减小步长,因此收敛的过程中不需要改变学习率
。示意图如下。
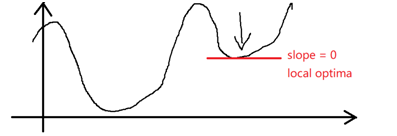
at local optima。经过学习获得的是局部最优解。
3.5.4 梯度下降更新参数公式
由代价函数得到两个参数的偏导数函数。
当时,
。
当时,
。
四、多元线性回归 Multiple Features and Gradient Descent
4.1 多元线性归回的符号约定 Notation
约定多元线性回归问题中的符号定义。
训练集的大小。
特征的维度大小。
第i个训练用例。
第i个训练用例的第j维特征值。
4.2 多元线性回归 Linear Regression with Multiple Variables
多元线性回归的估值为
4.3 估值、代价函数、梯度下降
为了方便起见,我们给特征值增加一个维度,也就是。
特征值和参数都写作向量的形式:
估值写作矩阵相乘的形式:
代价函数:
同步更新参数,以使代价函数最小,对于每一个参数而言
也就是说
……………………
写作矩阵式
4.4 多元线性回归的矩阵描述
综合4.3中讨论的内容,我们这样定义,并给出多元线性回归的矩阵描述公式
满足
那么梯度下降过程公式为
4.5 平均值归一化 Mean Normalization
Feature Scaling: Get every feature into approximately a range .
使用梯度下降时,为了加速收敛,应将特征值进行缩放(Feature Scaling)。缩放的具体算法就是Mean Normalization平均值归一化。
Mean Normalization平均值归一化的具体做法是,取得某一维度上特征值的平均值,最大值
,最小值
。
进行缩放,使缩放后该维度上特征值的平均值接近于0。
注意:
- 平均值归一化算法只能对维度
的特征值进行,决不能对
进行。因为
是人为添加的,都等于1,归一化后
将全部被置为0。
- 使用了平均值归一化,必须要在这个过程中记录下每个特征的平均值和标准差。在梯度下降得到模型参数以后,给出新的测试样本,那么就要用这个平均值和标准差先对这个测试样本进行平均值归一化,再计算估值。否则,估值是错误的。
4.6 多项式拟合 Polynomial Regression
回归问题也可以采用多项式(开方)来进行拟合。
4.7 过拟合Overfit与欠拟合Underfit
机器学习问题解决的答案并不是唯一的,我们用一元线性回归可以得到一种估值,也可以用多项式拟合得到另一种估值,也可以用开方的拟合得到另一种估值。不同的估值并没有对错之分,完全取决于我们选择了什么样的模型来解决问题。
对于明显的采用一元线性回归或者开平方拟合就能解决的问题,如果非要使用多项式拟合,在给定的训练集上可能效果很好。但是,随着特征(输入)范围的扩大,拟合效果将可能出现较大偏差,这就是过拟合Overfit。同理,如果我们用一元线性回归(“直线”)去解决一个明显是多项式回归的问题,或者多项式拟合的阶数不够,就会走向另一个极端欠拟合Underfit。
因此,我们应当对训练集的数据进行预处理,剔除明显带有错误或者重大偏差的数据,并小心谨慎的选择解决问题的模型(恰拟合),避免过拟合或欠拟合。
4.8 一般等式、梯度下降和一般等式的比较
根据,我们得出一个求参数
的一般等式。过程并不是严格的数学证明,只是一种演示,不严谨不要喷我。
这样我们不需要经过梯度下降,根据这个公式进行矩阵运算即可求得参数。如果使用octave或者matlab等软件,对于求矩阵逆的运算应使用pinv函数,以防止矩阵
不可逆。
最后对比一下梯度下降和一般等式的优缺点。
Gradient Decent 梯度下降 | Normal Equation 一般等式 |
|---|---|
Need to choose 需要选择学习率 | No Need to choose 不需要选择学习率 |
Need many iterations 需要迭代 | No need to iterate 不需要迭代 |
Work well even when n is large 当参数个数n较大时依然性能良好 | Need to compute slow if n is large 需要求矩阵的逆 当参数个数n较大时计算缓慢 |
相关文章:
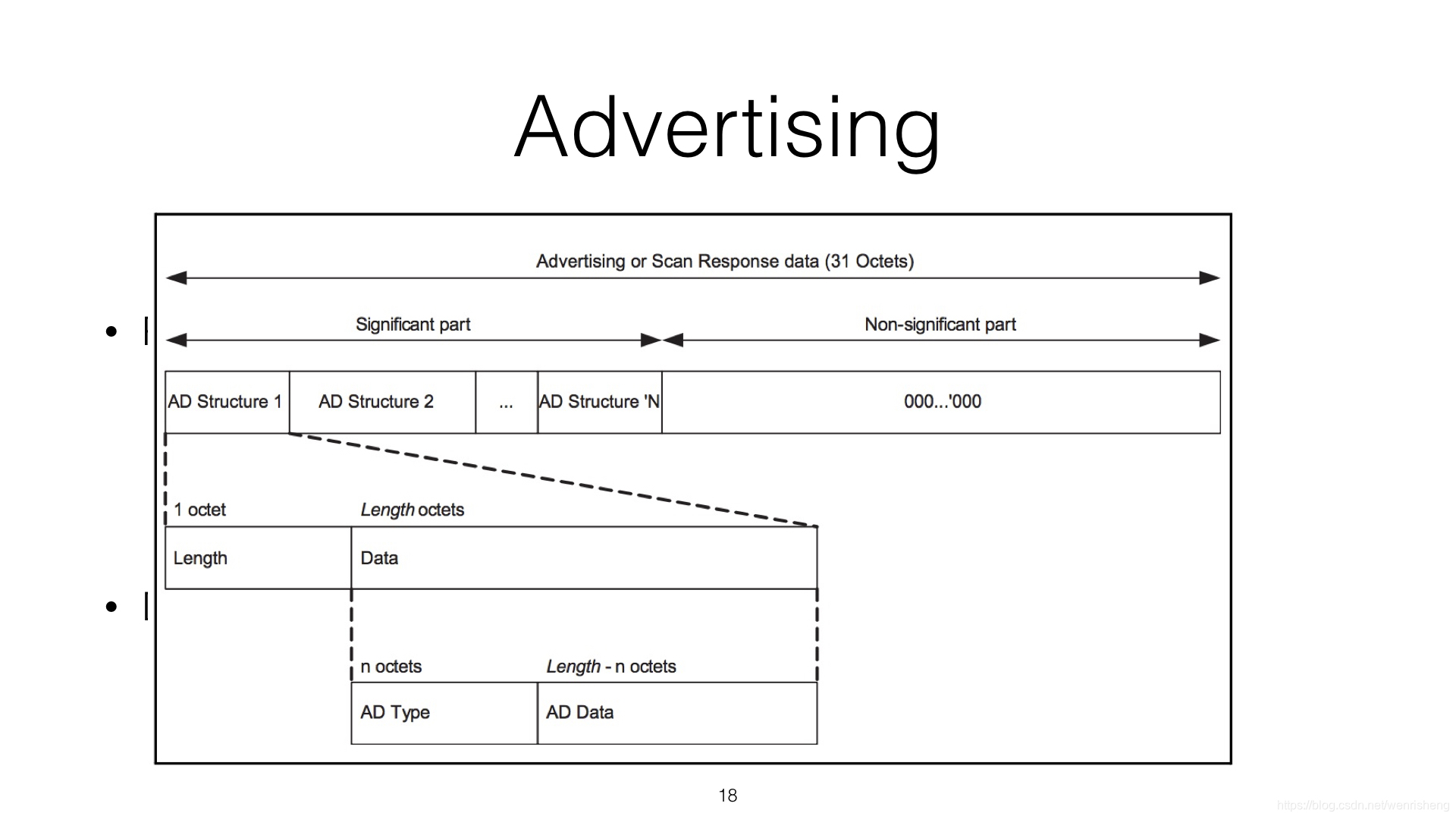
android专题-蓝牙扫描、连接、读写
android专题-蓝牙扫描、连接、读写 概念 外围设备 可以被其他蓝牙设备连接的外部蓝牙设备,不断广播自身的蓝牙名及其数据,如小米手环、共享单车、蓝牙体重秤 中央设备 可以搜索并连接周边的外围设备,并与之进行数据读写通讯,…

2 并发编程--开启进程的两种方式
multiprocessing 英 /mʌltɪprəʊsesɪŋ/ n. [计][通信] 多重处理 1、multiprocessing 模块介绍 python中的多线程无法利用多核优势,如果想要充分地使用多核CPU的资源(os.cpu\_count\(\)查看),在python中大部分情况需要使用多…

POJ 2112 Optimal Milking(二分+最大流)
POJ 2112 Optimal Milking 题目链接 题意:给定一些机器和奶牛,在给定距离矩阵,(不在对角线上为0的值代表不可达),每一个机器能容纳m个奶牛。问全部奶牛都能挤上奶,那么走的距离最大的奶牛的最小…
ajax的loading方法,Ajax加载中显示loading的方法
使用ajaxStart方法定义一个全局的“加载中。。。”提示$(function(){$("#loading").ajaxStart(function(){$(this).html.("");});$("#loading").ajaxSuccess(function(){$(this).html.("");// $(this).empty(); // 或者直接清除});});…
机器学习02-分类、逻辑回归
目录 一、分类问题 Classification 二、分类问题的估值 Hypothesis Representation 三、分类问题的决策边界 Decision Boundary 四、分类问题的代价函数 Cost Function 五、简化的代价函数与梯度下降Simplified Cost Function & Gradient Descent 5.1 简化代价函数 …

python绘制盖尔圆并做特征值的隔离
本程序并非智能到直接运行隔离出所有特征值,而是需要高抬贵手,手动调节变换矩阵D的参数,以实现特征值的隔离。若期待直接找到能特征值隔离的D矩阵参数变化范围,怕足下要失望了,鄙人暂没有做到那一步,一是因…

mysql 电商项目(一)
mysql 电商项目 - MySQL数据库开发规范 1、数据库基本设计规范 2、索引设计规范 3、数据库字段设计规范 4、数据库SQL开发规范 5、数据库操作行为规范 转载于:https://www.cnblogs.com/Eric15/articles/9719814.html

Android专题-常用第三方框架
Android专题-常用第三方框架 HTTP网络请求 带*号的是个人推荐比较好用的 HTTP网络请求 okhttp * :https://github.com/square/okhttp retrofit:https://github.com/square/retrofit Volley:https://github.com/google/volley Android Async HTTP:https://github.com/andr…

WPF显示经常使用的几个显示文字控件TextBox, TextBlock, Lable
WPF显示经常使用的几个显示文字控件TextBox, TextBlock, Lable TextBox, TextBlock。 Lable 当中TextBox 和Lable均继承了Control类 能够对其进行模板编辑。而TextBlock没有继承Control所以不能对其进行模板编辑 我的程序中须要做一个二级菜单…
机器学习03-神经网络
目录 一、非线性估值Non-Linear Hypothesis 二、神经网络建模 Neural Network 三、复习逻辑回归问题矩阵式 3.1 没有进行正则化 3.2 进行正则化 四、神经网络的代价函数 4.1 符号约定Notation 4.2 代价函数 五、反向传播算法 Backpropagation Alg 5.1 任务 5.2 一个…

python 打包
一、下载 pip install Pyinstaller 二、使用Pyinstaller 1、使用下载安装的方式安装的Pyinstaller打包方式 将需要打包的文件放在解压得到的Pyinstaller文件夹中,打开cmd窗口,把路径切换到当前路径打开命令提示行,输入以下内容(最…

iOS架构篇-3 网络接口封装
iOS架构篇-3 网络接口封装 关键字:iOS,网络接口封装,Alamofire,swift 网络接口API通常都需要自己封装一套管理,这里以swift版的Alamofire为例. 实现功能: 1.暴露参数请求地址url、请求方法method、请求参数params、请求头header、请求响应response(响应数据、响应头resp…

coursera 《现代操作系统》 -- 第十一周 IO系统
本周要求 错题 下列I/O控制方式中,哪一个不需要硬件支持? 中断方式 轮询方式 DMA方式 I/O处理机方式 中断方式:中断控制器 轮询方式:CPU不断查询设备以了解其是否就绪 DMA:使用到了 DMA 控制器 4。 在设备管理中,缓冲…

matlab图形绘制基础(东北大学MOOC笔记)
%% 二维图形绘制 % 多纵轴曲线绘制 figure(1); t 0:0.01:2*pi; y1 sin(t); y2 10*cos(t); % plotyy(t, y1, t, y2); yyaxis left plot(t, y1); ylim([min(y1), max(y1)]); yyaxis right plot(t, y2); ylim([min(y2), max(y2)]);% 绘制极坐标图 figure(2); theta 0 : 0.01 :…

【转载】pycharm远程调试配置
pycharm远程调试配置https://www.cnblogs.com/liangjiongyao/p/8794324.html

Tornado 类与类组合降低耦合
转载于:https://www.cnblogs.com/shiluoliming/p/6760548.html
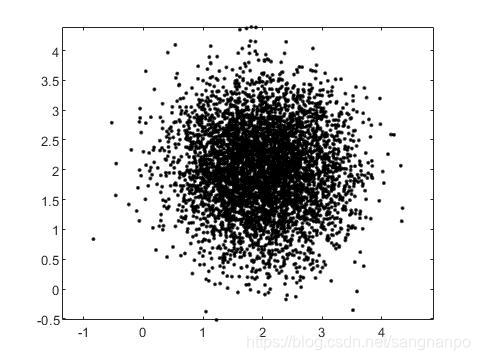
matlab生成多组多维高斯分布数据
matlab生成多组多维高斯分布数据 之所以写这么一个函数,是因为在练习用matlab实现聚类分析,用matlab生成的高斯分布数据可以作为很好的数据。当然,直接load进鸢尾花数据集也可以拿来练手,到后边再对鸢尾花数据集进行分析。 代码…

Android架构篇-5 CI/CD(持续集成、持续交付、持续部署)
Android架构篇-5 CI/CD(持续集成、持续交付、持续部署) CI CI是指持续集成,代码的更新会定期自动构建、测试并合并到公共仓库中,方便多分支时解决冲突问题 CD CD是指持续交付和/或持续部署,开发人员改动代码会自动测试提交到仓库,运维实施人员将其部署到生产环境中,方…

OpenCV中图像以Mat类型保存时各通道数据在内存中的组织形式及python代码访问各通道数据的简要方式...
OpenCV中图像以Mat类型保存时各通道数据在内存中的组织形式及python代码访问各通道数据的简要方式 以最简单的4 x 5三通道图像为例,其在内存中Mat类型的数据组织形式如下: 每一行的每一列像素的三个通道数据组成一个一维数组,一行像素组成一个…

CV01-语义分割笔记和两个模型VGG ResNet的笔记
目录 一、语义分割 二、VGG模型 2.1 VGG特征提取部分 2.2 VGG图像分类部分 三、ResNet模型 3.1 为什么是ResNet 3.2 11卷积调整channel维度大小 3.3 ResNet里的BottleNeck 3.4 Global Average Pooling 全局平均池化 3.5 Batch Normalization 学习语义分割理论&#x…

matlab编程实现k_means聚类(k均值聚类)
1. 聚类的定义 以下内容摘抄自周志华《机器学习》 根据训练数据是否拥有标记信息,机器学习任务可以大致分为两大类:“监督学习”(supervised learning)和“无监督学习”(unsupervised learning)。分类和回…

一目了然了解JAVA集合体系
在编程中,常常需要集中存放多个数据。从传统意义上讲,数组是我们的一个很好的选择,前提是我们事先已经明确知道我们将要保存的对象的数量。一旦在数组初始化时指定了这个数组长度,这个数组长度就是不可变的,如果我们需…

杭电1175简单搜索 连连看
连连看 Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 34807 Accepted Submission(s): 8657 Problem Description “连连看”相信很多人都玩过。没玩过也没关系,下面我给大家介绍一下游戏规则&#…

IOS专栏目录
IOS 专栏目录 iOS基础篇 iOS高级篇 ios架构篇-1 项目组织架构 ios架构篇-2 国际化多语言 iOS架构篇-3 网络接口封装 iOS架构篇-4 架构模式MVVM iOS架构篇-5 CI/CD(持续集成、持续交付、持续部署) iOS专题1-蓝牙扫描、连接、读写 iOS 直播专题1-直播流程原理 iOS 直播专题2-…
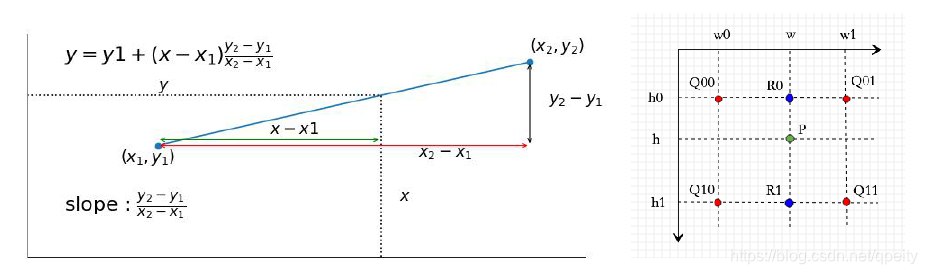
CV03-双线性差值pytorch实现
一、双线性差值 1.1 公式 在理解双线性差值(Bilinear Interpolation)的含义基础上,参考pytorch差值的官方实现注释,自己实现了一遍。 差值就是利用已知点来估计未知点的值。一维上,可以用两点求出斜率,再…
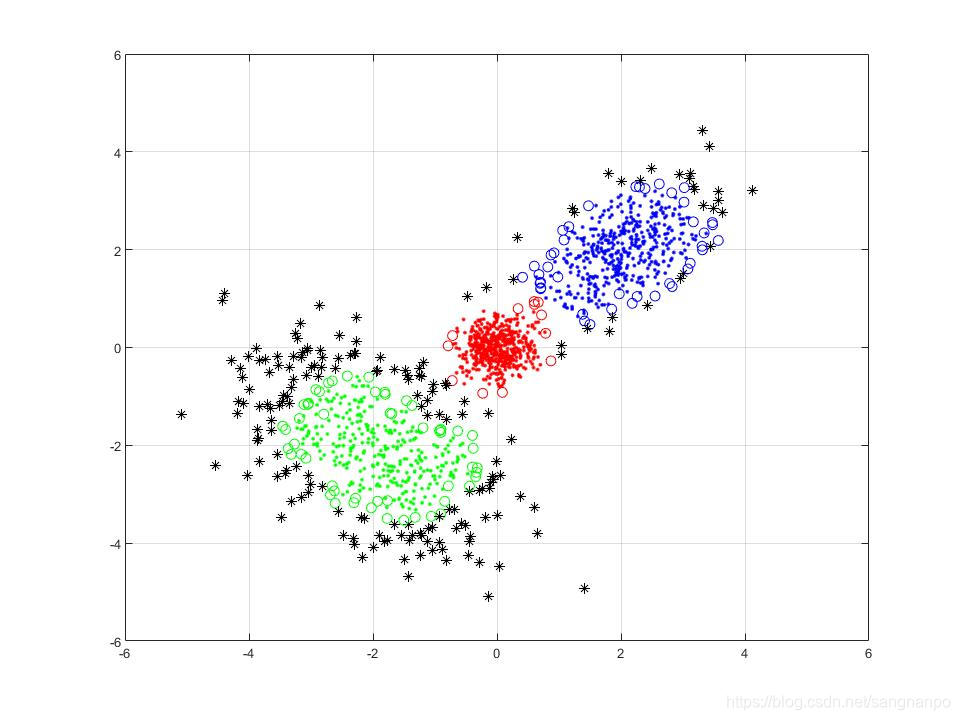
matlab编程实现基于密度的聚类(DBSCAN)
1. DBSCAN聚类的基本原理 详细原理可以参考链接: https://www.cnblogs.com/pinard/p/6208966.html 这是找到的相对很详细的介绍了,此链接基本仍是周志华《机器学习》中的内容,不过这个链接更通俗一点,且算法流程感觉比《机器学习…

EAST 自然场景文本检测
自然场景文本检测是图像处理的核心模块,也是一直想要接触的一个方面。刚好看到国内的旷视今年在CVPR2017的一篇文章:EAST: An Efficient and Accurate Scene Text Detector。而且有开放的代码,学习和测试了下。 题目说的是比较高效࿰…

通过httpmodule获取webapi返回的信息
我写了一个webapi,想在module中获取请求的信息和返回的信息,写进log里,以方便以后查询。request信息很容易能拿到,但是返回信息得费一番周折。不多说,上代码 public class ResponseLoggerModule : IHttpModule {privat…

iOS SwiftUI篇-2 UI控件 Text Button Image List
iOS SwiftUI篇-2 UI控件 Text Button Image List Text 显示文本,相当于UILabel import SwiftUIstruct TextContentView: View {var body: some View {//VStack(垂直排列视图)可以将其内部的多个视图,在垂直方向进行等距排列,VStack最多可以容纳十个子视图,VStack(spacin…

numpy和torch数据操作对比
对numpy和torch数据操作进行对比,避免遗忘。 ndarray和tensor import torch import numpy as npnp_data np.arange(6).reshape((2, 3)) torch_data torch.arange(6) # 张量 tensor2array torch_data.numpy()print(\nnumpy array:\n, np_data,\ntorch tensor\n,…
