机器学习02-分类、逻辑回归
目录
一、分类问题 Classification
二、分类问题的估值 Hypothesis Representation
三、分类问题的决策边界 Decision Boundary
四、分类问题的代价函数 Cost Function
五、简化的代价函数与梯度下降Simplified Cost Function & Gradient Descent
5.1 简化代价函数
5.2 梯度下降推导及结论
5.3 梯度下降 Advanced Optimization
六、多类别分类
七、过拟合问题
7.1 What is overfitting
7.2 Addressing overfitting
7.3 正则化后的代价函数
7.4 正则化线性回归 Regularized Linear Regression
7.5 正则化逻辑回归 Regularized Logistc Regression
复习Andrew Ng的课程Machine Learning,总结分类、逻辑回归笔记一篇,涵盖课程week3。
一、分类问题 Classification
线性回归可以对连续的模型进行估值(比如房价和房屋面积的关系),对于离散的模型估值(是为1,否为0)存在诸多问题。
- 对于分类问题,线性回归容易被个别训练样本影响
- 线性回归的估值
或
没有明确的意义
因此,分类问题引入逻辑回归Logistic Regression。于是,分类的最终输出是或
。逻辑回归的估值必须是一个值域
的函数,用做分类问题的算法
二、分类问题的估值 Hypothesis Representation
我们希望逻辑归回的估值满足,于是引入两个函数
令
从而得到分类问题的估值
对于这个估值的解释是这样的。在给定的情况下,对
的概率的估计值。
,probability that
,given
,parameterized
。
那么,当时,
;当
时,
。

举个栗子,是肿瘤大小的训练集。
表示有70%的概率,该肿瘤是恶性的。
三、分类问题的决策边界 Decision Boundary
根据前面讨论的结果。
估值
如果分类边界本身就是线性(Logistic Boundary Linear)的,即,取
,boundary是
,那么得到决策边界是
,是个直线方程。
如果分类边界本身是非线性(Logistic Boundary Non-Linear)的,即,取
,boundary是
,那么得到决策边界是
。

四、分类问题的代价函数 Cost Function
这里面涉及到一些数学知识。知道写下这篇博客,我还没有从数学层面上理解Andrew Ng说的Convex Convergence的意义。当然了,Andrew Ng也说了数学层面上该如何解决。我们先关注一下直觉上的Cost Function。
为逻辑回归选择一个Convex Convergence的代价函数,形式如下。
为什么是这种形式呢?我们直觉感受一下。也就是Andrew Ng所说的Cost Function Intuition。
当时,
越接近1,
越接近于0。
当时,
越接近0,
越接近于0。
这就达到了估值越接近真值,代价函数越接近0。这张示意图的代码可以到这里下载//download.csdn.net/download/qpeity/12113456。

五、简化的代价函数与梯度下降Simplified Cost Function & Gradient Descent
5.1 简化代价函数
第四节里面描述的内容是针对一个训练样本而言的。
注意:或
对每个训练样本只有一个成立。上面的公式简化为
对于有个样本的训练集,给出代价函数
。
也就是
5.2 梯度下降推导及结论
与线性回归问题一样,我们求得代价函数关于参数各个维度的导数,推导过程如下:
- 已知式
- 对
求偏导数得到
- 结合
对
中求内倒数部分进一步推导得到
- 将
代入
得到
就是步长。为了使代价函数最小,我们要同步更新
,不断迭代直到找到局部最优解,这就是最终的结论
。公式
和线性回归中同步更新
的公式形式上完全一样,只是
改变了。
5.3 梯度下降 Advanced Optimization
对于求解梯度下降,可以使用Naive的Gradient Descent。但是,这样Naive的实现方法效率并不高,计算也不够简单。
Andrew Ng给出了三种Advanced Optimization的方法,这些已经超出了机器学习课程的范围,具体怎么实现这些算法,他本人也是刚刚搞得明白(给大神跪了Orz)。这三种Advanced Optimization就是:
- Conjugate Gradient(共轭梯度?)
- BFGS
- L-BFGS
使用这些Advanced Optimization的优点是:
- 不需要人工选择学习率
- 比Naive的Gradient Descent更快
使用这些Advanced Optimization的缺点是:
- 算法更复杂
课程中,Andrew Ng建议,不要自己设计逻辑回归代价函数梯度下降的算法。这些算法异常复杂。除非你在数值计算领域特别的牛逼!!最好使用octave内置的函数库来做这些!!怎么来利用octave内置函数呢?我们举个例子。
逻辑回归的参数,假设逻辑回归的代价函数是
,分别求偏导数
然后用octave内置函数fminunc来求解。
六、多类别分类
将多类别分类变成二分类(One-vs-Rest):
- 将
分类变成
个二分类问题
- 每次分两类:
类、其余
类的合并
- 每次都形成新的伪训练集,求出
One-vs-Rest示意图。

此时,估值函数的形式和意义发生了一些变化。对每个分类我们训练一个估值
,用来预测
的概率。当有一个新的特征
输入时,我们用所有的
做估值,取概率最大的那个作为分类的估值。原文描如下:
- Train a logistic regression classifier
for each class
to predict the probability that
.
- On a new input
, to make a prediction, pick the class
that maximized
.
七、过拟合问题
7.1 What is overfitting
Overfitting: If we have too many features, the learned hypothesis may fit the training set very well(), but fail to generalize to new example(predict on new examples).
当特征过多时就会出现过拟合问题,这里的特征过多指的是:
- 特征的多项式维数过高
或者
- 特征太多,
7.2 Addressing overfitting
Options:
1.Reduce number of feature:
- Manually select which features to keep
- Model selection algorithm(Later in course)
2.Regularization:
- Keep all the features, but reduce magnitude / values of parameters
- Works well when we have a lot of features, each of which contributes a bit to predicting y.
翻译一下,解决过拟合问题有两种可选的办法:
1.减少特征数量:
- 人工选择要保留的特征(减少特征)
- 模型选择算法(后面会讲到,这里暂不讨论)
2.正则化:
- 保留所有特征,但减小参数
的量级
- 当有很多特征时正则化性能更好,每个特征都会在预测时体现价值
7.3 正则化后的代价函数
正则化就是想办法让变小,当
时,
就几乎不起作用了。线性回归代价函数变为如下形式。
经过正则化后的代价函数,多了一个,我们称
为Regularization Parameter正则化参数。代价函数由两部分组成:
- 前一部分
用来适应训练集;从1到m共m个训练集
- 后一部分
用来减小参数
的量级,防止过拟合;从1到n共n个特征。
为什么不限制呢?观察
,其中
不随特征
的变化而改变
的值,因此不限制
。
同理,逻辑回归的代价函数变为如下形式。
7.4 正则化线性回归 Regularized Linear Regression
由于代价函数中加入了,所代价函数的导数以及梯度下降都发生了变化。由于
项不会因
变化对
造成影响,导数和梯度下降公式分为两类。
导数:
梯度下降:
或者写作
基于Normal Equation的矩阵式经过正则化以后变为
其中,后面的那个矩阵P,迹1,1位置为0,迹其他位置全部是1,除了迹以外其余元素为0的矩阵。
7.5 正则化逻辑回归 Regularized Logistc Regression
逻辑回归的梯度下降和现行回归的形式一样,这个5.2节中已经推导。增加了正则化项以后,逻辑回归梯度下降公式在形式上和线性回归梯度下降也是一致的,只是的含义不同了。
导数:
梯度下降:
相关文章:

python绘制盖尔圆并做特征值的隔离
本程序并非智能到直接运行隔离出所有特征值,而是需要高抬贵手,手动调节变换矩阵D的参数,以实现特征值的隔离。若期待直接找到能特征值隔离的D矩阵参数变化范围,怕足下要失望了,鄙人暂没有做到那一步,一是因…

mysql 电商项目(一)
mysql 电商项目 - MySQL数据库开发规范 1、数据库基本设计规范 2、索引设计规范 3、数据库字段设计规范 4、数据库SQL开发规范 5、数据库操作行为规范 转载于:https://www.cnblogs.com/Eric15/articles/9719814.html

Android专题-常用第三方框架
Android专题-常用第三方框架 HTTP网络请求 带*号的是个人推荐比较好用的 HTTP网络请求 okhttp * :https://github.com/square/okhttp retrofit:https://github.com/square/retrofit Volley:https://github.com/google/volley Android Async HTTP:https://github.com/andr…

WPF显示经常使用的几个显示文字控件TextBox, TextBlock, Lable
WPF显示经常使用的几个显示文字控件TextBox, TextBlock, Lable TextBox, TextBlock。 Lable 当中TextBox 和Lable均继承了Control类 能够对其进行模板编辑。而TextBlock没有继承Control所以不能对其进行模板编辑 我的程序中须要做一个二级菜单…
机器学习03-神经网络
目录 一、非线性估值Non-Linear Hypothesis 二、神经网络建模 Neural Network 三、复习逻辑回归问题矩阵式 3.1 没有进行正则化 3.2 进行正则化 四、神经网络的代价函数 4.1 符号约定Notation 4.2 代价函数 五、反向传播算法 Backpropagation Alg 5.1 任务 5.2 一个…

python 打包
一、下载 pip install Pyinstaller 二、使用Pyinstaller 1、使用下载安装的方式安装的Pyinstaller打包方式 将需要打包的文件放在解压得到的Pyinstaller文件夹中,打开cmd窗口,把路径切换到当前路径打开命令提示行,输入以下内容(最…

iOS架构篇-3 网络接口封装
iOS架构篇-3 网络接口封装 关键字:iOS,网络接口封装,Alamofire,swift 网络接口API通常都需要自己封装一套管理,这里以swift版的Alamofire为例. 实现功能: 1.暴露参数请求地址url、请求方法method、请求参数params、请求头header、请求响应response(响应数据、响应头resp…

coursera 《现代操作系统》 -- 第十一周 IO系统
本周要求 错题 下列I/O控制方式中,哪一个不需要硬件支持? 中断方式 轮询方式 DMA方式 I/O处理机方式 中断方式:中断控制器 轮询方式:CPU不断查询设备以了解其是否就绪 DMA:使用到了 DMA 控制器 4。 在设备管理中,缓冲…

matlab图形绘制基础(东北大学MOOC笔记)
%% 二维图形绘制 % 多纵轴曲线绘制 figure(1); t 0:0.01:2*pi; y1 sin(t); y2 10*cos(t); % plotyy(t, y1, t, y2); yyaxis left plot(t, y1); ylim([min(y1), max(y1)]); yyaxis right plot(t, y2); ylim([min(y2), max(y2)]);% 绘制极坐标图 figure(2); theta 0 : 0.01 :…

【转载】pycharm远程调试配置
pycharm远程调试配置https://www.cnblogs.com/liangjiongyao/p/8794324.html

Tornado 类与类组合降低耦合
转载于:https://www.cnblogs.com/shiluoliming/p/6760548.html
matlab生成多组多维高斯分布数据
matlab生成多组多维高斯分布数据 之所以写这么一个函数,是因为在练习用matlab实现聚类分析,用matlab生成的高斯分布数据可以作为很好的数据。当然,直接load进鸢尾花数据集也可以拿来练手,到后边再对鸢尾花数据集进行分析。 代码…

Android架构篇-5 CI/CD(持续集成、持续交付、持续部署)
Android架构篇-5 CI/CD(持续集成、持续交付、持续部署) CI CI是指持续集成,代码的更新会定期自动构建、测试并合并到公共仓库中,方便多分支时解决冲突问题 CD CD是指持续交付和/或持续部署,开发人员改动代码会自动测试提交到仓库,运维实施人员将其部署到生产环境中,方…

OpenCV中图像以Mat类型保存时各通道数据在内存中的组织形式及python代码访问各通道数据的简要方式...
OpenCV中图像以Mat类型保存时各通道数据在内存中的组织形式及python代码访问各通道数据的简要方式 以最简单的4 x 5三通道图像为例,其在内存中Mat类型的数据组织形式如下: 每一行的每一列像素的三个通道数据组成一个一维数组,一行像素组成一个…

CV01-语义分割笔记和两个模型VGG ResNet的笔记
目录 一、语义分割 二、VGG模型 2.1 VGG特征提取部分 2.2 VGG图像分类部分 三、ResNet模型 3.1 为什么是ResNet 3.2 11卷积调整channel维度大小 3.3 ResNet里的BottleNeck 3.4 Global Average Pooling 全局平均池化 3.5 Batch Normalization 学习语义分割理论&#x…

matlab编程实现k_means聚类(k均值聚类)
1. 聚类的定义 以下内容摘抄自周志华《机器学习》 根据训练数据是否拥有标记信息,机器学习任务可以大致分为两大类:“监督学习”(supervised learning)和“无监督学习”(unsupervised learning)。分类和回…

一目了然了解JAVA集合体系
在编程中,常常需要集中存放多个数据。从传统意义上讲,数组是我们的一个很好的选择,前提是我们事先已经明确知道我们将要保存的对象的数量。一旦在数组初始化时指定了这个数组长度,这个数组长度就是不可变的,如果我们需…

杭电1175简单搜索 连连看
连连看 Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 34807 Accepted Submission(s): 8657 Problem Description “连连看”相信很多人都玩过。没玩过也没关系,下面我给大家介绍一下游戏规则&#…

IOS专栏目录
IOS 专栏目录 iOS基础篇 iOS高级篇 ios架构篇-1 项目组织架构 ios架构篇-2 国际化多语言 iOS架构篇-3 网络接口封装 iOS架构篇-4 架构模式MVVM iOS架构篇-5 CI/CD(持续集成、持续交付、持续部署) iOS专题1-蓝牙扫描、连接、读写 iOS 直播专题1-直播流程原理 iOS 直播专题2-…
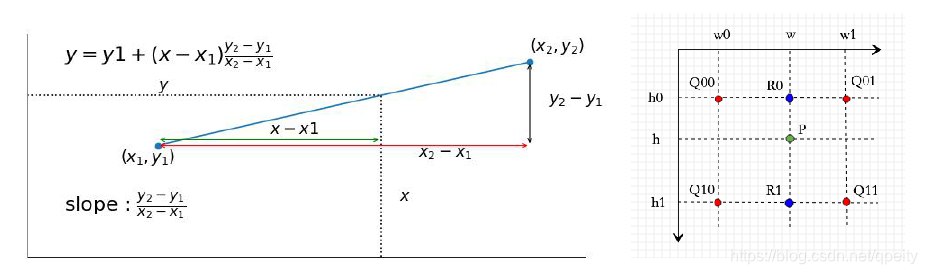
CV03-双线性差值pytorch实现
一、双线性差值 1.1 公式 在理解双线性差值(Bilinear Interpolation)的含义基础上,参考pytorch差值的官方实现注释,自己实现了一遍。 差值就是利用已知点来估计未知点的值。一维上,可以用两点求出斜率,再…
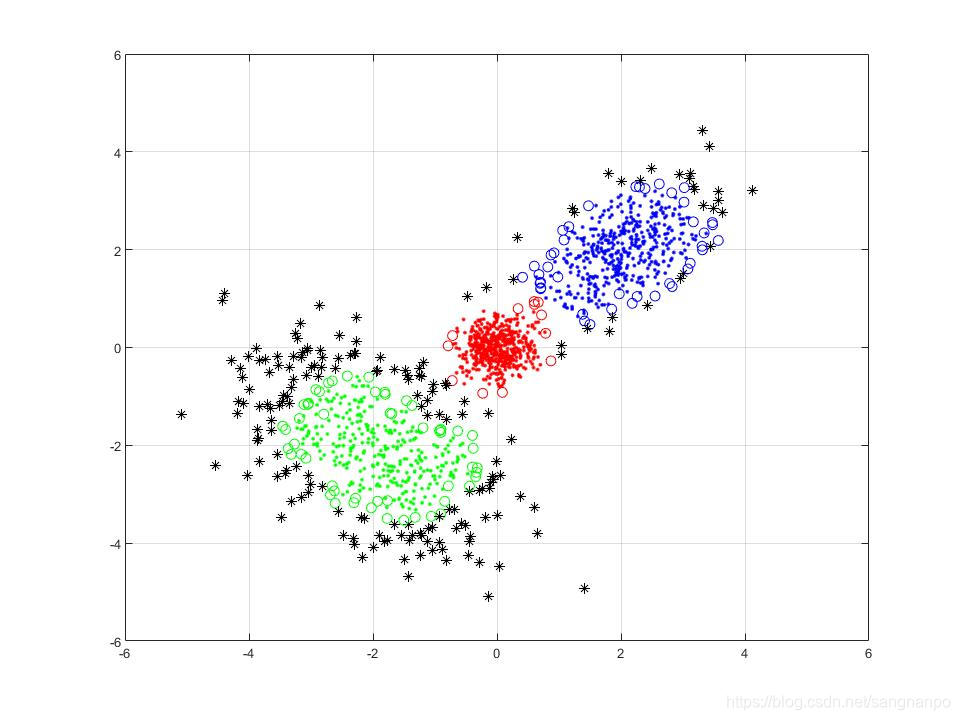
matlab编程实现基于密度的聚类(DBSCAN)
1. DBSCAN聚类的基本原理 详细原理可以参考链接: https://www.cnblogs.com/pinard/p/6208966.html 这是找到的相对很详细的介绍了,此链接基本仍是周志华《机器学习》中的内容,不过这个链接更通俗一点,且算法流程感觉比《机器学习…

EAST 自然场景文本检测
自然场景文本检测是图像处理的核心模块,也是一直想要接触的一个方面。刚好看到国内的旷视今年在CVPR2017的一篇文章:EAST: An Efficient and Accurate Scene Text Detector。而且有开放的代码,学习和测试了下。 题目说的是比较高效࿰…

通过httpmodule获取webapi返回的信息
我写了一个webapi,想在module中获取请求的信息和返回的信息,写进log里,以方便以后查询。request信息很容易能拿到,但是返回信息得费一番周折。不多说,上代码 public class ResponseLoggerModule : IHttpModule {privat…

iOS SwiftUI篇-2 UI控件 Text Button Image List
iOS SwiftUI篇-2 UI控件 Text Button Image List Text 显示文本,相当于UILabel import SwiftUIstruct TextContentView: View {var body: some View {//VStack(垂直排列视图)可以将其内部的多个视图,在垂直方向进行等距排列,VStack最多可以容纳十个子视图,VStack(spacin…

numpy和torch数据操作对比
对numpy和torch数据操作进行对比,避免遗忘。 ndarray和tensor import torch import numpy as npnp_data np.arange(6).reshape((2, 3)) torch_data torch.arange(6) # 张量 tensor2array torch_data.numpy()print(\nnumpy array:\n, np_data,\ntorch tensor\n,…
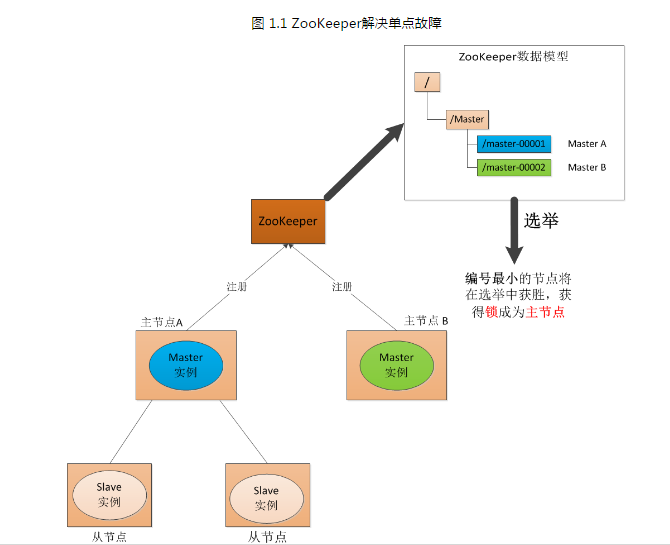
ZooKeeper学习
一、ZooKeeper 的实现 1.1 ZooKeeper处理单点故障 我们知道可以通过ZooKeeper对分布式系统进行Master选举,来解决分布式系统的单点故障,如图所示。 那么我们继续分析一下,ZooKeeper通过Master选举来帮助分布式系统解决单点故障, 保…
iOS SwiftUI篇-1 项目结构
iOS SwiftUI篇-1 项目结构 介绍Xcode新建的SwiftUI模版项目结构、跟普通Storyboard模版项目的差异、SwiftUI项目的app启动流程、UIScene概念介绍、AppDelegate.swift和Info.plist的差异 1.项目模版 Interface: SwiftUI Life Cycle: UIKit App Delegate Language: Swift Life…

js绑定事件和解绑事件
在js中绑定多个事件用到的是两个方法:attachEvent和addEventListener,但是这两个方法又存在差异性 attachEvent方法 只支持IE678,不兼容其他浏览器addEventListener方法 兼容火狐谷歌,不兼容IE8及以下 addEventListener方法 div.addEventListener(click,fn); div.addEventLi…

基于三维点云数据的主成分分析方法(PCA)的python实现
主成分分析(PCA)获取三维点云的坐标轴方向和点云法向量 # 实现PCA分析和法向量计算,并加载数据集中的文件进行验证import open3d as o3d # import os import numpy as np from scipy.spatial import KDTree# from pyntcloud import PyntClo…
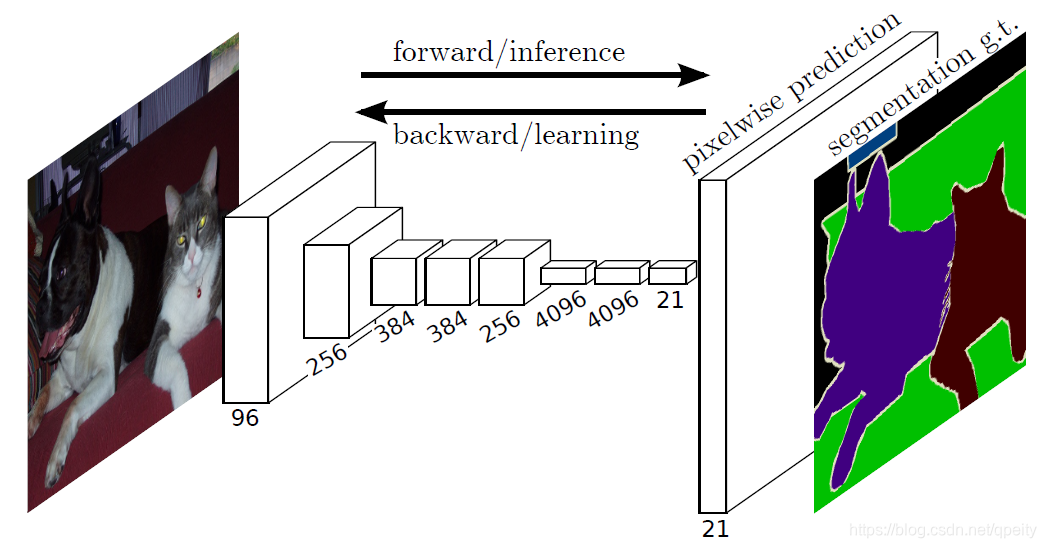
CV02-FCN笔记
目录 一、Convolutionalization 卷积化 二、Upsample 上采样 2.1 Unpool反池化 2.2 Interpolation差值 2.3 Transposed Convolution转置卷积 三、Skip Architecture 3.1 特征融合 3.2 裁剪 FCN原理及实践,记录一些自己认为重要的要点,以免日后遗…
