算法设计与分析之循环与递归
前言:
循环与递归可以说是算法设计中最基本但却也是最重要的工具方法。循环和递归对于学习过高级程序设计语言的人来说都并不陌生,但还是有必要仔细的探究一下循环和递归之间的相似和区别。循环与递归最大的相似之处莫不是在于他们在算法设计中的工具作用,它们都起到了“以不变应万变”的作用。“不变应万变”不正是程序设计的核心内容吗?正因为如此,更有必要探究一下这两种不同的设计工具的区别。本文先从利用循环和递归工具设计算法时的设计要点来认识循环和递归,然后再给出几个具体的实例来说明循环和递归的差异和优劣。
1.循环设计要点
循环设计的要点可以概括为三个部分:效率、正向思维、具体到抽象。下面以不同的具体实例来讨论这三个要点。
1.1效率
例1.1 求1/1!-1/3!+1/5!-1/7!+....+(-1)^(n+1)/(2n-1)!
算法1:使用二重循环实现,循环不变式为:s(n)=s(n-1)+(-1)^(n+1)/(2n-1)!。这样的算法的时间复杂度为O(n^2)。针对本题有没有时间复杂度为O(n)的算法呢?
算法2:循环不变式:s(n)=s(n-1)+(-1)^(n+1)A(n); A(n)=A(n-1)*1/((2*n-2)*(2*n-1))。这个算法的时间复杂度为O(n)。其C++代码实现如下:
#include <iostream>
using namespace std;
int main(void){
int n;
cout<<"Please input a number:"<<endl;
cin>>n;
float sum=1; //存储结果
float t=1;// 存储阶乘
int sign=1; //存储负号
//循环
for(int i=2; i<=n; i++){
sign=-sign;
t=t*(2*i-2)*(2*i-1);
sum+=sign/t;
}
cout<<"Result is: "<<sum<<endl;
}
1.2正向思维
正向思维的方法是从全局到局部、从概略到详细的设计方法。是对一个问题由整体到分解和细化的方法。这也是循环设计的一般方法。下面求完数的例子可以说明正向思维设计要点的过程。
例1.2 一个数如果恰好等于它的因子之和(包括1但不包括这个数本身),这个数就成为完数。
1)顶层算法
for(i=1; i<=n; i++){
判断i是否为完数;
是完数,输出;
}
2)判断i是否为完数的算法
for(j=2; j<i; j++)
计算i的因子,并累加;
如果累加的值为i,输出i;
3)进一步细化判断i是否为完数的算法
s=1;
for(j=2; j<i; j++){
if(i mod j ==0)
s += j;
}
if(s==i)
输出i;
1.3具体到抽象
具体到抽象的方法也可以说成是数学归纳法。数学归纳法可以说是算法设计中非常重要的一种方法。算法设计的本质,可以说就是在看似杂乱无章的信息中总结归纳出一种不变的规律,以不变应万变。下面的这个打印规则图形的例子可以说明这点。
例1.3 打印具有下图规律的图形
1
5 2
8 6 3
10 9 7 4
算法C++实现如下:
#include<iostream>
#define N 10
using namespace std;
int main(void){
int a[N+1][N+1];
int k=1;
for(int i=1; i<=N; i++)
for(int j=1; j<=N+1-i; j++)
a[i+j-1][j]=k++;
for(int i=1; i<=N;i++){
for(int j=1; j<=i; j++)
cout<<a[i][j]<<" ";
cout<<endl;
}
}
2.递归设计要点
递归设计方法,也可以叫做逆向思维方法(对比与循环设计的正向思维)。递归设计通常有以下三个步骤:
(1)寻找递归关系:找出大规模问题于小规模问题的关系,这样通过递归是问题的规模逐渐变小。
(2)找出递归停止的条件,即算法可解的最小规模问题。
(3)设计函数,确定函数所需参数。
下面给出一个整数划分问题的递归算法设计:
列2.1 求一个整数划分的种类数。列如6有11种划分如下:
6
5+1
4+2 4+1+1
3+3 3+2+1 3+1+1+1
2+2+2 2+2+1+1 2+1+1+1+1
1+1+1+1+1+1+1
算法描述及C++实现:
/*
*定义一个函数Q(n,m)表示整数n的任何加数都不超过m的划分数目
*n的所有划分数目P(n)就应该表示为Q(n,n).
*
*一般Q(n,m)有如下递归关系:
*Q(n,n)=1+Q(n,n-1);
*Q(n,m)=Q(n,m-1)+Q(n-m,m)
*右边第一部分表示不包含m的划分,第二部分表示包含m的划分
*那么就意味着剩下的部分就是对n-m进行不超过m的划分。
*
*递归的停止条件:
*Q(n,1)=1,表示当最大的被加数是1时,该整数n只有一种划分
*Q(1,m)=1,表示整数1只有一个划分,不管最大被加数的上限
*是多少。
*
*算法的稳健性:
*如果n<m,则Q(n,m)是无意义的,此时Q(n,m)=Q(n,n)
*同样的当n<1或m<1时,Q(n,m)也是无意义的。
*/
#include<iostream>
using namespace std;
int Divinteger(int n, int m){
if( n<1||m<1 )//错误条件
cout<<"Error input!"<<endl;
else if( n==1||m==1 )//停止条件
return 1;
else if( n<m )//稳健条件
return Divinteger(n, n);
else if( n==m )// Q(n,n)=1+Q(n,n-1)
return (1+Divinteger(n, n-1));
else //Q(n,m)=Q(n,m-1)+Q(n-m,m)
return (Divinteger(n, m-1)+Divinteger(n-m, m));
}
int main(void){
int n;
cout<<"Please input a number:"<<endl;
cin>>n;
cout<<"Result is: "<<Divinteger(n,n)<<endl;
}
3.循环与递归的比较
这个部分以不同的例子引出三个结论。
3.1结论1:在具体实现时,方便的情况下应该把递归算法转化成等价的循环结构算法,以提高算法的时空效率。
例3.1 将一个十进制整数由低位到高位按位输出。
/*
* 将一个十进制整数从低位到高位逐位输出
* 循环不仅在时间而且在空间效率均高于递
* 归程序。
*/
void for_low_to_high(int n){
while(n){
cout<<n%M<<" ";
n=n/M;
}
cout<<endl;
}
void f_ltoh(int n){
if(n<M)
cout<<n<<endl;
else{
cout<<n%M<<" ";
f_ltoh(n/M);
}
}
例3.2 将一个十进制整数由高位到低位按位输出。
/*
* 将一个十进制整数从高位到低位逐位输出
* 循环与递归空间效率一样,虽然时间效率
* 有差异,但递归程序间单可读性好。
*/
void for_high_to_low(int n){
int i=0;int a[16];
while(n){
a[i]= n%M;
n=n/M;
i++;
}
for(int j=i-1; j>=0; j--)
cout<<a[j]<<" ";
cout<<endl;
}
void f_htol(int n){
if(n<M)
cout<<n<<" ";
else{
f_htol(n/M);
cout<<n%M<<" ";
}
}
3.2结论2:当问题需要后进先出的操作时,还是递归算法更有效 。如树的遍历和图的深度优先算法等都是如此。所以不能仅仅从效率上评价两种控制重复操作机制的好坏。
例3.3 用2的幂次方表示一个正整数。例如:137=2^7+2^3+2^0,则137可表示为: 2(7)+2(3)+2(0),进一步:7=2^2+2+2^0,3=2+2^0 所以137可表示为:2(2(2)+2+2(0))+2(2+2(0))+2(0) 。
算法的C++实现:
#include<iostream>
using namespace std;
void tryf(int n, int r=0){//n为数,r为深度
if(n==1)//递归结束条件
cout<<"2("<<r<<")";
else{//n除以2,深度加1
tryf(n/2,r+1);
if(n%2==1)//如果余数不为0输出2的r幂次
cout<<"+2("<<r<<")";
}
}
void tryff(int n, int r=0){
if(n==1){
switch(r){
case 0:cout<<"2(0)";break;
case 1:cout<<"2";break;
case 2:cout<<"2(2)";break;
default:{cout<<"2(";tryff(r, 0);cout<<")";}
}
}else{
tryff(n/2, r+1);
if(n%2==1){
switch(r){
case 0:cout<<"+2(0)";break;
case 1:cout<<"+2";break;
case 2:cout<<"+2(2)";break;
default:{cout<<"+2(";tryff(r, 0);cout<<")";}
}//switch
}//if
}//else
}
int main(void){
int n;
cout<<"Please input a number:"<<endl;
cin>>n;
if(n>1){
tryf(n);
cout<<endl;
tryff(n);
}else
cout<<"Inupt Error!"<<endl;
}
3.3结论3:递归是一种强有力的算法设计工具。递归是一种比循环更强、更好用的实现重复操作的机制。因为递归不需要编程者自己构造循环不变式,而只需找出递归关系和最小问题的解。递归在很多算法策略中得以运用,如分治策略、动态规划、图的搜索等算法策略。
由下面的例子可以看出递归的层次可以控制的,而循环嵌套的层次只能是固定的。
例3.4 找出n个自然数(1,2,3,4,5,.....,n)中取r个数的组合。
算法C++实现:
#include <iostream>
#define N 5
#define R 3
using namespace std;
void for_fun1(){
int t=0;
for(int i=1; i<=N; i++)
for(int j=1; j<=N; j++)
for(int k=1; k<=N; k++)
if( (i<j) && (j<k) ){
t++;
cout<<i<<" "<<j<<" "<<k<<endl;
}
cout<<"Total= "<<t<<endl;
}
//more efficiency
void for_fun2(){
int t=0;
for(int i=1; i<=N-R+1; i++)
for(int j=i+1; j<=N-R+2; j++)
for(int k=j+1; k<=N-R+3; k++){
t++;
cout<<i<<" "<<j<<" "<<k<<endl;
}
}
//recruisive
int a[100];
int t=0;
void comb(int n, int r){
for(int i=n; i>=r; i--){//循环n-r+1次
a[r]=i;//n中选r个数,确定第一个数
if(r>1){//递归深度为r
comb(i-1,r-1);
}
else{//结束条件为深度r等于1
for(int j=a[0]; j>0; j--)
cout<<a[j]<<" ";
cout<<endl;
t++;
}
}
} //算法复杂度O(n*r)
void rec_fun(){
a[0]=R;
comb(N,R);
cout<<"Total= "<<t<<endl;
}
int main(void){
for_fun1();
for_fun2();
rec_fun();
}
最后对递归说明一点,递归可以说是一种算法策略,也可以说是一种算法设计的工具,不管从哪一方面来看对算法设计都是很好的帮助。递归在很多算法策略中得以运用,如分治策略、动态规划、图的搜索等算法策略。有很多数据结构都是具有递归定义的,如链表,队列,栈,二叉树。
转载于:https://blog.51cto.com/remyspot/1333215
相关文章:

面向对象与软件工程---团队作业1
1.队伍名称: 遥遥万里(还有很长路要走的意思) 2.队员信息: 陈雄(组长) 学号:1700509024 博客园链接:https://www.cnblogs.com/bearchan/ 廖鹏辉 学号:1700802007 博客园…
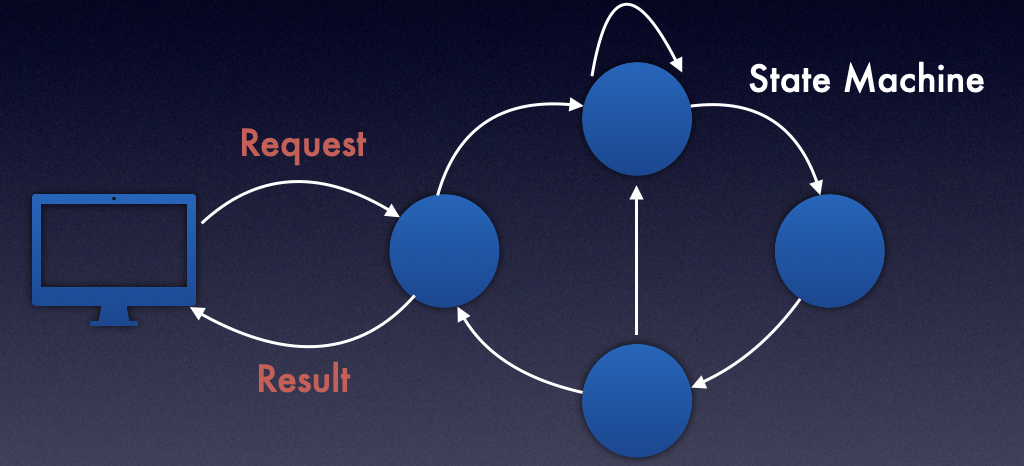
从paxos到raft zab,为何raft能够“独领风骚”
文章目录RAFT出现的缘由RAFT 的实现STATE MACHINELog Replicated State MachineLeader Election基本角色关键变量基本选举过程Log Replicated基本概念基本操作SafetyLog Replication: Consistency checkLeader Election: Leader Completeness总结RAFT 和 ZAB 的对比参考文献:阅…
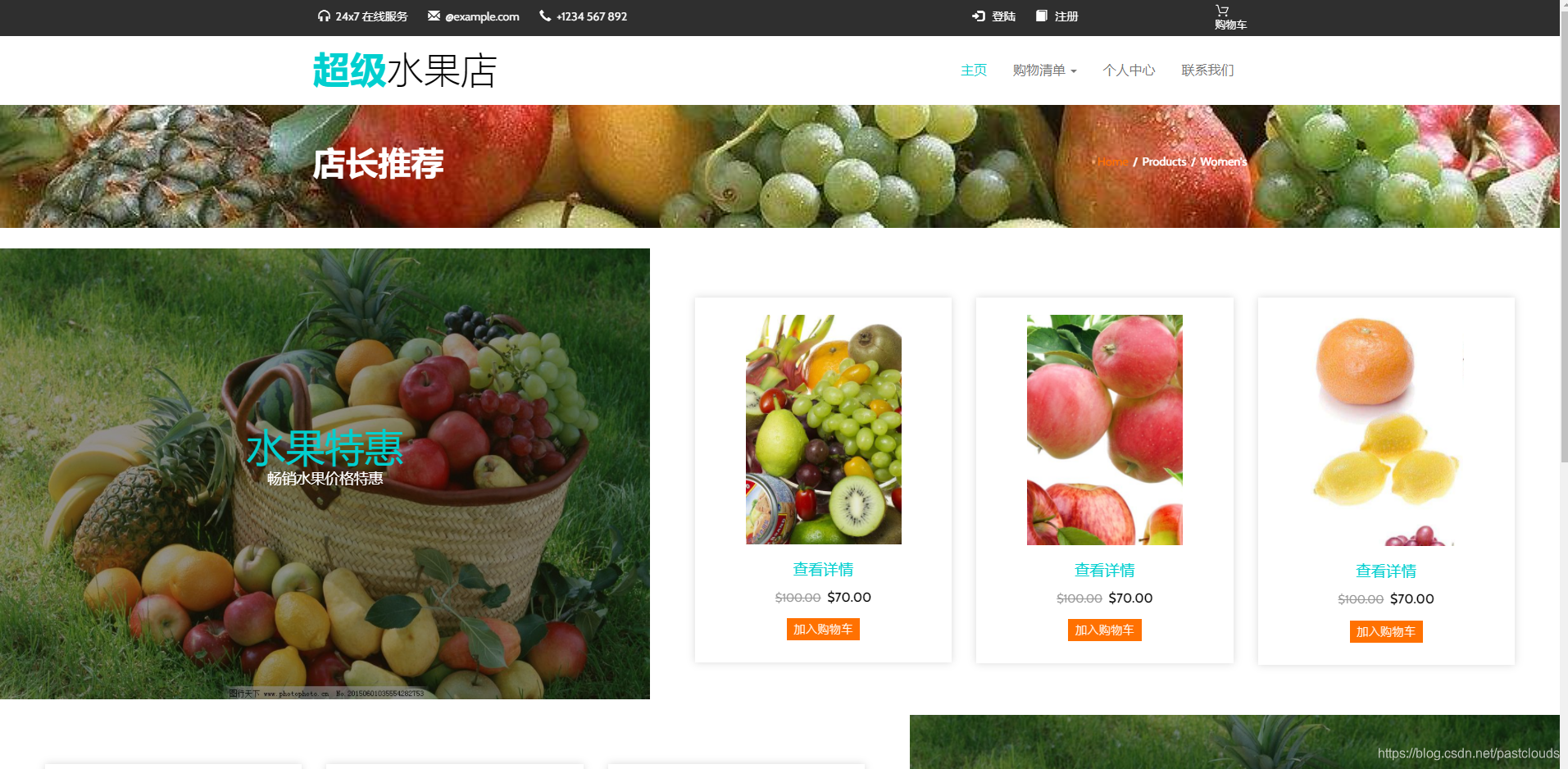
Java项目:前台+后台精品水果商城系统设计和实现(java+Springboot+ssm+mysql+jsp+maven)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统主要实现的功能有: 前台用户的登录注册,水果商品的展示,水果的购物车, 购物车新增结算等等,银行卡的支付绑定,收货…
Android屏幕像素密度适配详解
讲到像素密度,我们先要搞明白什么是像素密度,像素密度的字面上的意思为手机屏幕上一定尺寸区域内像素的个数。在Android开发中, 我们一般会使用每英寸像素密度(dpi)这样一个单位来表示手机屏幕的像素密度,d…

如让自己想学不好shell编程都困难?
众所周知,shell是linux运维必备的技术,必须要掌握,但是shell语法复杂,灵活,网友掌握了语法也不知道如何应用到实际运维中,老男孩培训shell编程给所有linux运维人员带来了学好shell的法宝,老男孩培训2014最新…

sqlserver可将字符转成数字再进行sum,如果varchar类型中存放的都是数字
sqlserver语法: select sum(cast(score as int)) as score from 表名; 注意:int是整型,在实际操作中根据自己需要的类型转换。转载于:https://www.cnblogs.com/MisMe/p/10690748.html
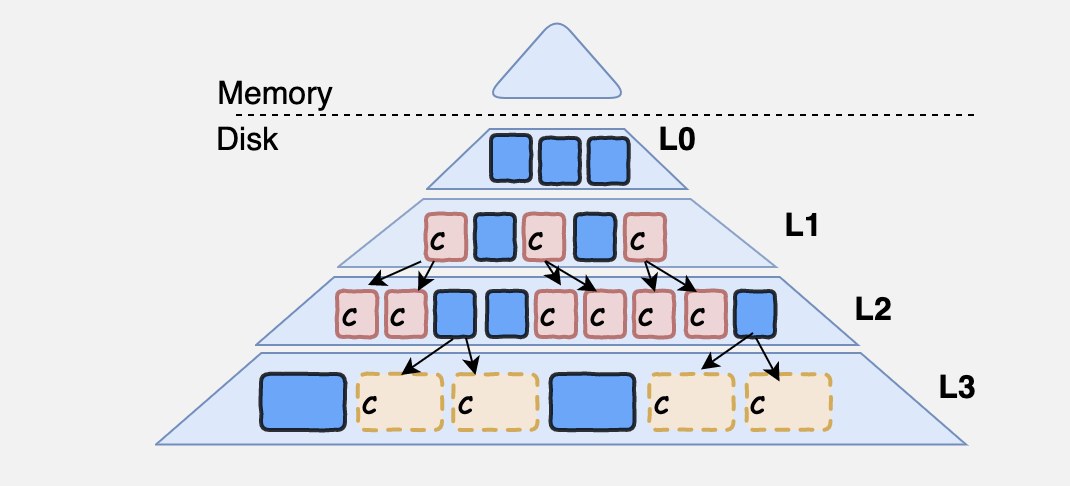
LSM 优化系列(六)-- 【ATC‘20】MatrixKV : NVM 的PMEM 在 LSM-tree的write stall和写放大上的优化
文章目录LSM 问题背景MatrixKV 设计细节整体架构介绍Matrix Container介绍ReceiverRowTableCompactorSpace managementColumn Compaction介绍对于Column Compaction的总结读加速 Cross-row Hint SearchMatrixKv 写入完整流程MatrixKV 读取完整流程MatrixKV 性能总结这篇论文大家…
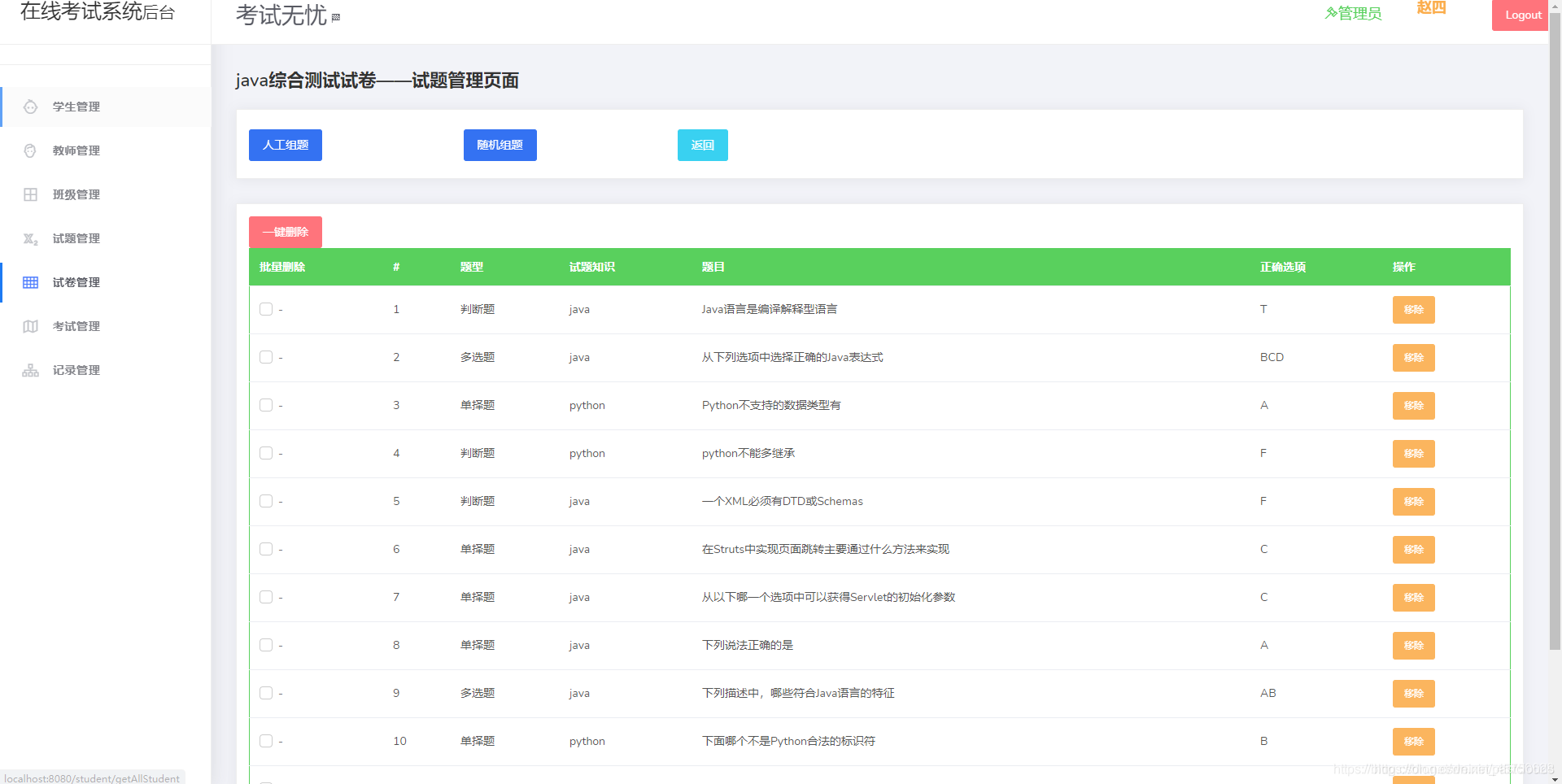
Java项目:前台+后台在线考试系统设计和实现(java+Springboot+ssm+mysql+jsp+maven)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统主要实现的功能有: 学生以及老师的注册登录,在线考试,错题查询,学生管理,问题管理,错题管理,错题查询…

修改nginx服务器类型
通常nginx服务器不隐藏服务器类型及版本信息 curl -I http://www.aaa.com 获取web服务器的类型和版本代码 HTTP/1.1 200 OK Server: nginx nginx/0.8.53 Date: Tue, 14 Dec 2010 08:10:06 GMT Content-Type: text/html Content-Length: 151 Last-Modified: Mon, 13 Dec 2…

JS 自带函数
JS数组方法汇总 array数组元素的添加和删除js数组元素的添加和删除一直比较迷惑,今天终于找到详细说明的资料了,先给个我测试的代码^-^var arr new Array();arr[0] "aaa";arr[1] "bbb";arr[2] "ccc";//alert(arr.leng…
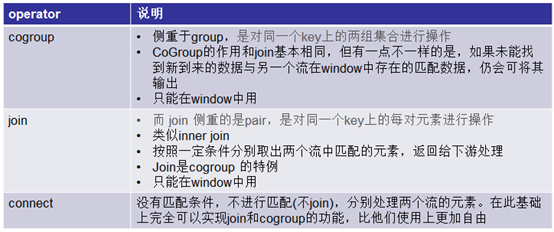
Flink学习笔记:Operators之CoGroup及Join操作
本文为《Flink大数据项目实战》学习笔记,想通过视频系统学习Flink这个最火爆的大数据计算框架的同学,推荐学习课程: Flink大数据项目实战:http://t.cn/EJtKhaz 1. Window CoGroup与Join 1.1回顾RDBMS各种join 假设有两个表A和B 1.…

Rocksdb 的优秀代码(二)-- 工业级 打点系统 实现分享
文章目录前言数据结构选型打点代码设计耗时打点请求计数打点打点总结前言 一个完善的分布式系统一定是需要完善的打点统计,不论是对系统内核 还是 对系统使用者都是十分必要的。系统的客户需要直观得看到这个系统的性能相关的指标来决定是否使用以及如何最大化使用…

JVM中可生成的最大Thread数量
最近想测试下Openfire下的最大并发数,需要开大量线程来模拟客户端。对于一个JVM实例到底能开多少个线程一直心存疑惑,所以打算实际测试下,简单google了把,找到影响线程数量的因素有下面几个: -Xms intial java heap s…

Java项目:在线电影售票系统设计和实现(java+Springboot+ssm+mysql+jsp+maven)
源码获取:博客首页 "资源" 里下载! 一、项目简述 前台: 1、正在上映的电影浏览查看。 2、影院信息浏览查看。 3、新闻咨询信息浏览查看。 4、地域信息查看切换。 5、用户注册登录。 6、电影排期查看。 7、在线选座生成…

matlab正态分布
normrnd(mu, sigma, m,n) 返回m x n的随机数,正态分布均值mu,标准差sigma。 mvnrnd(mu, sigma, m) 返回m个随机数(点),是多元正太分布,mu是均值向量,sigma是协方差。 x normrnd(0,4,1,100000);…

MYSQL语句
-- 一、管理数据库-- 1.1 创建数据库CREATE DATABASE day15; SHOW DATABASES; CREATE TABLE student( id INT, NAME VARCHAR(20), age INT); -- 查看表SHOW TABLES; -- 二、管理数据-- 1.1插入数据(insert into)-- 需求: 往学生表插入数据INS…
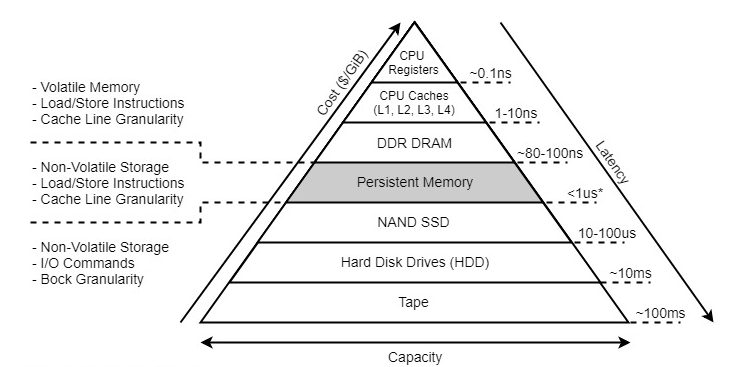
Intel Optane PMEM 概览
文章目录前言基本架构编程模型PMDK接口架构接口概览pmdk 安装开发文档汇总PMEM性能官方性能实测性能前言 随着以PCM 为存储单元的3D XPoint 非易失存储介质 不断精进的工艺,以及 上层硬件协议栈的飞速发展,为非易失内存这样硬件的出现提供了技术工艺基础…

Java项目:新闻发布系统(java+Springboot+ssm+mysql+maven)
源码获取:博客首页 "资源" 里下载! 一、项目简述 功能: 区分为管理员用户和普通用户,管理员用户能删除评论, 调整新闻显示/隐藏,修改新闻,删除普通用户,普通用户能 登陆浏…

Linux下搭建Lotus Domino集群
Linux下搭建Lotus Domino 集群本文内容是Linux平台下Lotus Domino服务器部署案例(http://chenguang.blog.51cto.com/350944/1334595)的另一个模块,所以大家首先要有以上基础之后然后继续实验。集群是 Lotus Domino Server 提供的最重要特性之…

Centos下卸载openjdk并安装自定义jdk
1、查看是否安装了openjdk java -version 2、查看需要卸载的openjdk信息,其中只需要删除红色框标记的地方 rpm -qa | grep java 3、删除openjdk rpm -e --nodeps 需要删除的java组件 4、创建文件夹java mkdir java 5、到官网下载linux版本的jdk(如果不能…

pmdk -- libpmemlog 介绍
文章目录1. libpmemlog 应用背景2. libpmemlog 使用方式2.1 基本接口2.2 接口使用3. Libpmemlog 性能3.1 write sys call 性能3.2 libpmemlog 性能1. libpmemlog 应用背景 本文介绍的是英特尔 傲腾持久化内存 pmdk中 的一个持久化日志的库。 我们正常系统中会将日志 形成一个…
Java项目:家庭财务管理系统(java+Springboot+ssm+mysql+maven)
源码获取:博客首页 "资源" 里下载! 一、项目简述 功能: 家庭财务管理系统,具有收入统计,支出统计,汇总报 表,工资录入,其他收入等录入开支信息,echart图标插 …

(原创)c++primer(第五版)--1.3 注释简介
注释可以帮助人类读者理解程序。注释通常用于概述算法,确定变量的用途,或者结束晦涩难懂的代码段。编译器会忽略注释,因此注释对程序的行为或者性能不会有任何影响。 虽然编辑器会忽略注释,但读者并不会。即使系统文档的其他部分已…

BZOJ 1503 郁闷的出纳员(splay)
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id1503 题意:给出一个数列(初始为空),给出一个最小值Min,当数列中的数字小于Min时自动删除。四种操作:(1)数列…

javascript ES6 新特性之 扩展运算符 三个点 ...
对于 ES6 新特性中的 ... 可以简单的理解为下面一句话就可以了: 对象中的扩展运算符(...)用于取出参数对象中的所有可遍历属性,拷贝到当前对象之中。 作用类似于 Object.assign() 方法,我们先来看一下 Object.assign() 方法: Obje…
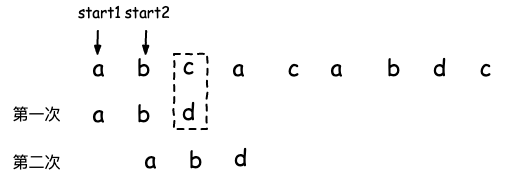
字符串匹配算法 -- BM(Boyer-Moore) 和 KMP(Knuth-Morris-Pratt)详细设计及实现
文章目录1. 算法背景2. BM(Boyer-Moore)算法2.1 坏字符规则(bad character rule)2.2 好后缀规则(good suffix shift)2.3 复杂度及完整代码3. KMP(Knuth Morris Pratt)算法3.1 好前缀 和 坏字符规则3.2 高效构建 失效函数3.3 复杂度…

Java项目:中小医院信息管理系统(java+Springboot+ssm+mysql+maven+jsp)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:实现了挂号收费,门诊管理,划价收 费,药房取药,体检管理,药房管理,系统维护等各个模块功能&a…

DB2load遇到SQL3508N错误
SQL3508N装入或装入查询期间,当存取类型为 "<文件类型>" 的文件或路径时出错。原因码:"<原因码>"。路径:"<路径/ 文件>"。 [more]解释: 装入或装入查询处理期间,在尝…
【cocos2d-x 手游研发小技巧(3)Android界面分辨率适配方案】
先感叹一下吧~~android的各种分辨率各种适配虐我千百遍,每次新项目我依旧待它如初恋 每家公司都有自己项目工程适配的方案,这种东西就是没有最好,只有最适合!!! 这次新项目专项针对android,目的…
git submodule 使用场景汇总
文章目录1. 前言2. 基础命令介绍2.1 场景一:已有仓库,添加一个子模块2.2 场景二:已有仓库,添加一个子模块的特定分支2.3 场景三:已有仓库,更新子模块内容2.4 场景四:已有仓库,变更子…
