字符串匹配算法 -- BM(Boyer-Moore) 和 KMP(Knuth-Morris-Pratt)详细设计及实现
文章目录
- 1. 算法背景
- 2. BM(Boyer-Moore)算法
- 2.1 坏字符规则(bad character rule)
- 2.2 好后缀规则(good suffix shift)
- 2.3 复杂度及完整代码
- 3. KMP(Knuth Morris Pratt)算法
- 3.1 好前缀 和 坏字符规则
- 3.2 高效构建 失效函数
- 3.3 复杂度及完整代码
- 4. 总结
1. 算法背景
文本编辑器/搜索引擎 随着处理的数据量的不断增加,对字符串匹配的效率要求越来越高,字符串匹配的效率也在不断演进。
传统的字符串匹配算法:BF(Brute Force) 和 RK(Rabin Karp) 算法 都消耗大量的时间。其中BF 比较粗暴,会将主串中的每一个字符都和模式串进行比较。RK在其基础上做了优化,虽然不再一个一个字符比较,而是从主串中构建模式串长度的子串hash,从而达到高效的hash比较,但是构建每个子串的hash值的过程同样需要取m-n+1个子串,并且对其计算hash,代价同样巨大。
以上两种字符串匹配算法满足不了我们在大数据量下文本编辑器的查找性能(vim / less / more 的内容查找),对字符串匹配高效性能的需求 促进了BM/KMP这样的高效匹配算法的出现。核心匹实现 还是说 每一次发现主串和模式串不匹配的字符之后,尽可能在主串中移动多个一定不会匹配的字符。
当然,目前BF,RK,BM,KMP 这样的算法能够在单模式串之间完成匹配,也就一个主串,一个模式串之间的匹配。对于 文本编辑器,像VIM这样的 还需要有多模式串之间的高性能匹配需求,也就是一个主串多个模式串之间的匹配。所以,Trie树这样的数据结构 以及 AC 自动机这样的高效算法 应运而生,并且他们被广泛应用在了搜索引擎之中。
本篇将带你欣赏 高效的单模式串匹配算法 BM和KMP。
2. BM(Boyer-Moore)算法
像背景中介绍的BF/RK 算法,核心还是对主串中的一个一个字符进行匹配,如下图,如果第一次匹配到c发现模式串对应下标为d不匹配了,则会回到主串的第二个字符作为重新开始匹配的起始字符。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pYBdsKaW-1612373995282)(/Users/zhanghuigui/Library/Application Support/typora-user-images/image-20210202110143901.png)]](https://img-blog.csdnimg.cn/20210204014248147.png)
更加高效的匹配方式应该是跳过一定不会匹配的字符,比如上图中主串的b和c ,直接将主串的起始匹配字符向后移动到a开始进行匹配,这样能够有效减少匹配次数。
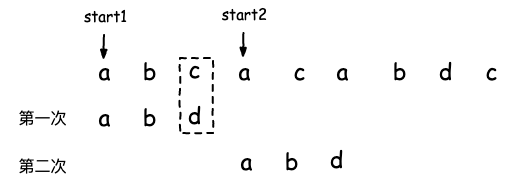
所以BM算法是为了找到能够保证不会漏过匹配可能性的情况下 高效移动的规律。
主要就是两种规则:
- 坏字符
- 好后缀
2.1 坏字符规则(bad character rule)
一般情况下,我们完成字符串匹配的过程是从左向右进行匹配的,比较符合我们的思维习惯,而坏字符规则 是反向 从右向左进行匹配。
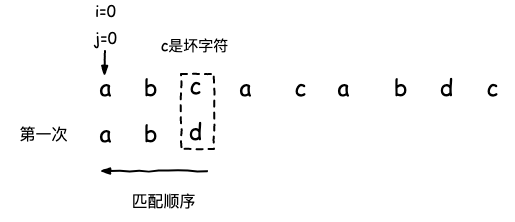
先匹配最右边的字符,发现主串c和模式串d不匹配,则认为c是坏字符,接下来模式串的移动将向后滑动三位,移动到坏字符之后。仍然从右向左进行匹配,发现主串中的a和模式串的d不匹配。
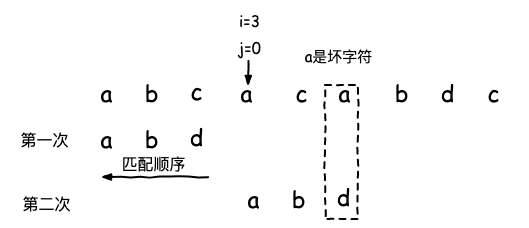
接下来的移动则不能直接移动到坏字符之后,因为模式串中也有一个a,如果我们直接移动到主串坏字符之后,就错过了匹配, 应该将模式串向后滑动两位,如下:
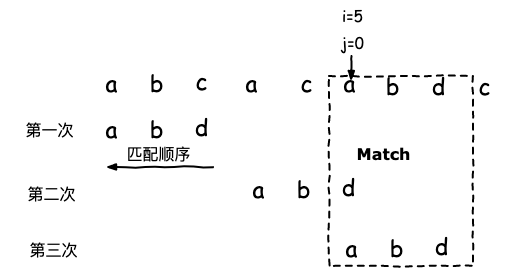
所以坏字符规则下的算法移动方式如下:
- 从右向左匹配模式串和主串,发现坏字符
ch时记录 此时对应模式串的下标Si - 检测模式串中是否有ch,有的话将其下标记录
Xi,否则记录Xi = -1 - 移动时 直接移动
Si - Xi的长度
比如上图 的算法移动方式如下:
- 第一次发现坏字符时
Si=2;Xi=-1,则直接将模式串滑动Si-Xi=3 - 第二次发现坏字符时
Si=2;,因为模式串存在字符a,所以Xi=0,最后移动Si-Xi=2次 - 第三次 Match
实现代码:
generateBC函数会预先记录模式串中每一个字符的index,如果有两个一样的字符,将后一个字符的下标作为index(防止匹配漏掉)bm_alg函数中先从右向左,发现不匹配的字符,记录该字符对应的模式串下标; 从mp中取坏字符在模式串中存在的index,相减即可。
// storage the des's position
//
// @params:
// des: destination string
// mp: update the relationship between char in
// des with it's index in des
//
// examples:
// s t r _ e x a m p l e
// 0 1 2 3 4 5 6 7 8 9 10
//
// mp['s'] = 0
// ...
// mp['e'] = 10
// ....
void generateBC(string des, map<char ,int> &mp) {int i;for(i = 0;i < des.size(); i ++) {// and the map relationship between des's// element with it's positionmp[des[i]] = i; }
} int bm_alg(string src, string des) {map<char ,int> last_pos;generateBC(des, last_pos);int i=0;int src_len = src.size();int des_len = des.size();while (i <= (src_len - des_len)) {int j;// find the bad charfor (j = des_len - 1; j >= 0; j--) {if (src[i+j] != des[j]) {break;}}if (j < 0) {return i;}// bad char's move positionint x = j - last_pos[src[i+j]];// move the max of position between badchari = i + x;}return -1;
}
坏字符实现的最好时间复杂度能够达到O(n/m),尤其是主串和模式串有类似特点的场景:aaabaaabaaabaaab 和 aaaa 这种情况下的匹配时十分高效的。
但是坏字符并不能处理所有的匹配情况,比如aaaaaaaaaaaaa和baaa这种情况,使用坏字符规则 下的滑动位置会变成负数(Si=0,Xi=3,滑动-3,显然不合理),所以BM算法还需要好后缀规则。
2.2 好后缀规则(good suffix shift)
当我们从右往左遍历模式串时找到坏字符时,前面已经相同的部分表示好后缀。
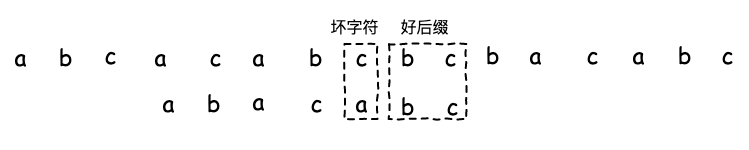
通过好后缀方式移动的算法有两种:
- 如果好后缀在模式子串v 中的另一个位置还存在v’,则将模式子串的v’ 和主串的好后缀对齐。
- 如果好后缀不存在于模式串中的其他位置,则判断好后缀的后缀子串 是否包含在模式串的前缀子串中;包含,则移动模式串 使后缀子串和匹配的前缀子串对齐;否则,按照坏字符规则移动。
对于第一种算法,移动方式如下:
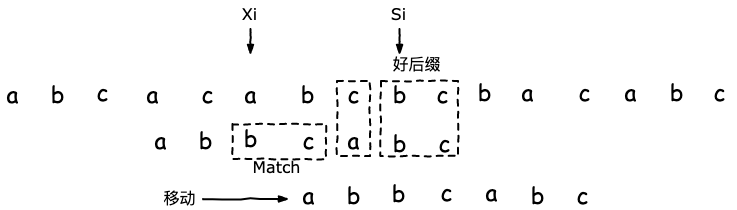
找到好后缀在模式串的起始下标Si,以及另一个在模式串中匹配的好后缀的起始下标Xi,最终移动Si - Xi。
为什么会有第二种判断好后缀的后缀子串的过程呢?如下匹配:

但实际上,这种情况已经过度滑动了,按照第一种移动方式会错过正确的结果。

第二种办法是取好后缀的后缀子串,判断其是否能够和模式串的前缀子串匹配,匹配则移动到两个子串相匹配的位置。
后缀子串表示最后一个字符相同,前缀子串表示第一个字符相同;比如:abcd的后缀子串为 d,cd,bcd;对应的前缀子串为 a,ab,abc。这两个指标是固定的,且能够在开始匹配前快速初始化模式串的所有后缀子串和前缀子串 ,已经其是否匹配。
构建过程如下:
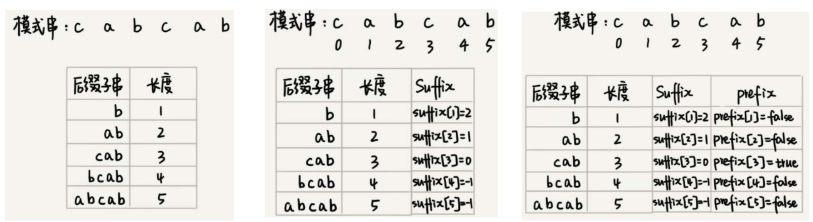
- suffix 数组下标表示 后缀子串的长度,值表示后缀子串在模式串中匹配的另一个子串的起始位置。比如
suffix[1]=2,后缀子串b长度为1,模式串中还有另一个b,则2表示这个b的其实下标。 - Prefix 数组 的bool值表示这个后缀子串是否和前缀子串匹配。
构建两个数组的代码如下:
// generate suffix and prefix arr
//
// @params:
// des: destination str
// suffix: the first position of the suffix str in des
// prefix: if the suffix exist in prefix of des, update
// prefix arr vector<bool> to true
//
// examples:
// des: b a b c a b
// pos: 0 1 2 3 4 5
// suffix: b, ab, cab, bcab, abcab
// suffix[1] = 0
// suffix[2] = 1
// suffix[3] = -1
// suffix[4] = -1
// suffix[5] = -1
//
// prefix[1] = true
// prefix[2] = true
// prefix[3] = false
// ...
void generateGS(string des, vector<int> &suffix,vector<bool> &prefix) {int i;int des_len = des.size();for (i = 0;i < des_len; i++) {suffix.push_back(-1);prefix.push_back(false);}// traverse the prefix str , update the suffix vector // and prefix vectorfor (i =0; i< des_len - 1; i++) {int j = i; // prefix start indexint k = 0;while(j >= 0 && des[j] == des[des_len - 1 -k]) {--j;++k;suffix[k] = j + 1;}if (j == -1) {prefix[k] = true;}}
}
完整好后缀的匹配规则 整体以尽可能短得方式移动:
- 判断好后缀u是否包含在模式串中的其他位置u’, 移动到u’的起始位置,结束。
- 判断好后缀的后缀子串v 是否包含在模式串的其他位置v’,并且和前缀子串匹配,则移动到前缀子串的起始位置,结束。
- 移动模式串长度 m 个位置,结束。

移动代码如下:
// move the des str to a position
//
// @params:
// j: bad char's index
// des: destination string
// suffix: suffix in des's start index
// prefix: wether the suffix math with prefix
//
// case:
// src: a b c a c a b c b c b a c a b c
// des: c b a c a b c
int movePosition(int j, string des, vector<int> suffix, vector<bool> prefix) {// case1: move to the longest len of sufix// 'k' is the good suffix's start index// 'j' is the bad char's indexint k = des.size() - 1 - j;if (suffix[k] != -1) {return j - suffix[k] + 1;}// case2: move to other suffix position//// longest suffix's range [j+1, len(des)-1]// other suffix's range [j+2, len(des)-1]for (int r = j + 2; r <= des.size() - 1; r++) {if (prefix[des.size() - r] == true) {return r;}}// case3: move the len of desreturn des.size();
}
在好后缀的移动规则和坏字符的移动规则之间取最大的移动位置来移动即可(好后缀的移动是普遍大于坏字符的移动方式),也就是好后缀的规则可以单独使用。
2.3 复杂度及完整代码
- 空间复杂度:使用额外的两个vector和一个map来保存中间数据。其大小与模式串的长度m有关。
- 时间复杂度:
- A new proof of the linearity of the Boyer-Moore string searching algorithm 证明最坏场景上限为O(5n)
- Tight bounds on the complexity of the Boyer-Moore string matching algorithm 证明最坏场景上限为O(3n)
source_code: https://github.com/BaronStack/DATA_STRUCTURE/blob/master/string/bm_alg.cc
完整代码实现如下:
#include <iostream>
#include <map>
#include <string>
#include <vector>#define MAP_SIZE 256using namespace std;// storage the des's position
//
// @params:
// des: destination string
// mp: update the relationship between char in
// des with it's index in des
//
// examples:
// s t r _ e x a m p l e
// 0 1 2 3 4 5 6 7 8 9 10
//
// mp['s'] = 0
// ...
// mp['e'] = 10
// ....
void generateBC(string des, map<char ,int> &mp) {int i;for(i = 0;i < des.size(); i ++) {// and the map relationship between des's// element with it's positionmp[des[i]] = i; }
} // generate suffix and prefix arr
//
// @params:
// des: destination str
// suffix: the first position of the suffix str in des
// prefix: if the suffix exist in prefix of des, update
// prefix arr vector<bool> to true
//
// examples:
// des: b a b c a b
// pos: 0 1 2 3 4 5
// suffix: b, ab, cab, bcab, abcab
// suffix[1] = 0
// suffix[2] = 1
// suffix[3] = -1
// suffix[4] = -1
// suffix[5] = -1
//
// prefix[1] = true
// prefix[2] = true
// prefix[3] = false
// ...
void generateGS(string des, vector<int> &suffix,vector<bool> &prefix) {int i;int des_len = des.size();for (i = 0;i < des_len; i++) {suffix.push_back(-1);prefix.push_back(false);}// traverse the prefix str , update the suffix vector // and prefix vectorfor (i =0; i< des_len - 1; i++) {int j = i; // prefix start indexint k = 0;while(j >= 0 && des[j] == des[des_len - 1 -k]) {--j;++k;suffix[k] = j + 1;}if (j == -1) {prefix[k] = true;}}
}// move the des str to a position
//
// @params:
// j: bad char's index
// des: destination string
// suffix: suffix in des's start index
// prefix: wether the suffix math with prefix
//
// case:
// src: a b c a c a b c b c b a c a b c
// des: c b a c a b c
int movePosition(int j, string des, vector<int> suffix, vector<bool> prefix) {// case1: move to the longest len of sufixint k = des.size() - 1 - j;if (suffix[k] != -1) {return j - suffix[k] + 1;}// case2: move to other suffix position//// longest suffix's range [j+1, len(des)-1]// other suffix's range [j+2, len(des)-1]for (int r = j + 2; r <= des.size() - 1; r++) {if (prefix[des.size() - r] == true) {return r;}}// case3: move the len of desreturn des.size();
}// boyer-moore algorithm
//
// two rules:
// 1. bad char
// 2. good suffix
int bm_alg(string src, string des) {if (src.size() == 0 || des.size() == 0) {return -1;}map<char ,int> last_pos;vector<int> suffix;vector<bool> prefix;generateBC(des, last_pos);generateGS(des, suffix, prefix);int i=0;int src_len = src.size();int des_len = des.size();while (i <= (src_len - des_len)) {int j;// find the bad charfor (j = des_len - 1; j >= 0; j--) {if (src[i+j] != des[j]) {break;}}if (j < 0) {return i;}// bad char's move positionint x = j - last_pos[src[i+j]];int y = 0;// good suffix's move positionif (j < des_len - 1) {y = movePosition(j, des, suffix, prefix);}// move the max of position between badchar and // good suffixi = i + std::max(x,y);}return -1;
} int main() {string src;string des;cout << "input src ";cin >> src;cout << "input des ";cin >> des;if (bm_alg(src, des) != -1) {printf("%s is the substr of %s with index : %d\n",des.c_str(), src.c_str(), bm_alg(src,des));} else {printf("not match \n");}return 0;
}
3. KMP(Knuth Morris Pratt)算法
有了之前对BM算法的理解,接下来再看KMP算法就事半功倍了。
BM算法中通过 坏字符 和 好后缀 规则 来约束模式串的滑动,两个规则的结合能够高效得检索模式串是否和主串匹配。KMP算法相比于BM算法 都希望加速模式串的滑动,提升匹配效率。不同的是KMP将好后缀规则变成了好前缀规则。
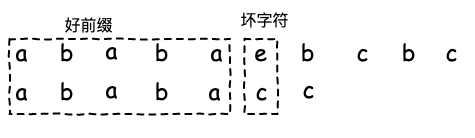
如上图,将模式串和主串中已经匹配的字符串称为好前缀,不同的字符同样是坏字符,就像BM算法的好后缀规则下,监测到好后缀的后缀子串在模式串中的其他位置,则向后滑动到这个匹配后缀子串的起始位置即可。同样,KMP的好前缀中也希望滑动到匹配的后缀子串的位置(为了避免滑动过多,跳过匹配的情况,这里选择最大匹配的后缀子串)。
3.1 好前缀 和 坏字符规则
如下图,取好前缀的最大匹配后缀子串,其长度为k,将模式串匹配的前缀子串的结尾index移动 j-k个位置 即能够和最大匹配后缀子串对齐,此事坏字符的位置i不用发生变化。
由上图可知,KMP的滑动除了需要依赖主串找到坏字符之外, 其他的最大匹配前缀子串的计算并不需要主串的参与,仅仅通过模式串就能够预先完成所有情况的最大匹配前缀子串的结尾下标计算。
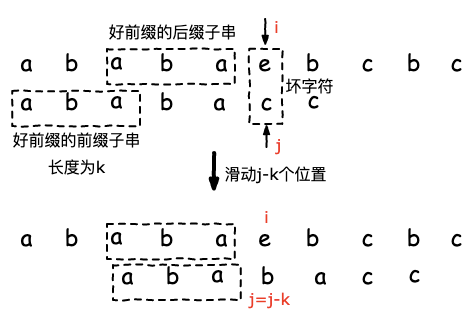
也就是我们在KMP的算法规则中 只需要知道当出现坏字符时,模式串的最大可匹配前缀的下标即可,这样就能够完成模式串的移动了。这个最大可匹配下标的计算也就是KMP 常说的失效函数的计算,属于KMP的核心计算过程了,我们将失效函数用next数组来表示。
基本的kmp代码实现如下:
int kmp_alg(string src, string des) {if (src.size() == 0 || des.size() <= 0) {return -1;}int src_len = src.size();int des_len = des.size();vector<int> next;int i, j;next.resize(des_len);// Get the next vectorgetNext(des,next);for (i = 0;i < src_len; i++) {// 1. Find the bad char// 2. Next[j-1] is the longest match prefix's tail index// move the j to the destinations.// // Example:// i// 0 1 2 3 4 5 6 7 8 9// src: a b a b a e a b a c// des: a b a b a c d // 0 1 2 3 4 5 6// j//// when find bad char: i = 5, j = 5;// good prefix is : ababa// longest match prefix : aba// longest match prefix tail in des: 2// next[j-1] : next[5-1] = 2// j: 2 + 1 = 3//// after slide ,the src and des is bellow:// i// 0 1 2 3 4 5 6 7 8 9// src: a b a b a e a b a c// des: a b a b a c d // 0 1 2 3 4 5 6// j// while(j > 0 && src[i] != des[j]) {j = next[j-1] + 1; }// The good prefix, just add the jif (src[i] == des[j]) {j++;}// Match the des and return the index in srsif (j == des_len) {return (i - des_len + 1);}}return -1;
}
接下来看一下如何构建失效函数这一部分。
3.2 高效构建 失效函数
如下图,左侧的图能够非常直观得看到 当发现了好前缀之后,如何找到其最大可匹配前缀的过程。
通过将好前缀的所有前缀子串和后缀子串列出来,找到其中最长一个能够完成匹配的前缀子串,即是我们的最长可匹配前缀子串。这个寻找过程,我们也可以用来直接构造如右侧图的next数组(失效函数),也就是暴力法。
暴力法就是 **要对模式串中的每一个好前缀(m-1个)都要分别找出其后缀子串和前缀子串,并从中找到能够匹配的最长的子串,**这个代价是极大的。

更优的办法 是使用next[i-1] 来 尝试构建next[i],理论上 next[i] 中肯定包含next[i-1],因为next[i]对应的好前缀是包含next[i-1]对应的好前缀的,这种方式理论上是可行的,需要关注的细节如下:
case1: 假如next[i-1] = k-1,也就是子串des[0,k-1]是des[0,i-1]的最长可匹配前缀子串。如果des[0,k-1]的下一个字符des[k]和 des[0,i-1]的下一个字符des[i] 相等,则next[i] = next[i-1] + 1= k。
case2: 如果des[0,k-1]的下一个字符des[k]和 des[0,i-1]的下一个字符des[i] 不相等,这个时候的处理稍微麻烦一些。
也就是des[0,k-1]中无法满足找到最长可匹配前缀子串,那么des[0,next[k-1]]的下一个字符能否满足等于des[i]的要求呢,即des[next[k-1]]和des[i]是否相等,想等则认为des[0,next[k-1]] 是 des[0,i]的最长可匹配前缀子串,next[i] = next[k-1]+1 。
整体上类似于数学的递推公式:
- 前一个的最长串des[0,k] 的下一个字符des[k+1]不与最后一个字符des[i]相等,则需要找前一个的次长串
- 问题也就变成了求des[0, next[k]]的最长串:如果下一个字符des[next[k] + 1]还不和des[i]相等,那么继续回溯到求des[0,next[next[k]]]的最长串,再判断des[next[next[k]] + 1]和des[i]是否相等,相等则next[i] = next[next[k]] + 1
- 否则继续,依此直到找到 能够和des[i]相等的字符。此时的next[next[…]]+1 就是next[i]的值。
next数组的求值代码如下:
void getNext(string des, vector<int> &next) {next[0] = -1;int k = -1;int i;// i begin with 1, next[0] always is -1for (i = 1; i< des.size(); i++) {// Find the longest match prefix by judge // two char dex[i] and des[k+1].// Just like case1 and case2: next[i-1]=k-1// if des[i] == des[k-1], then next[i] = next[i-1] + 1 = k;while(k != -1 && des[i] != des[k+1]) {//let 'k' storage 'next[next[...]]'k = next[k];}// find the match char, let k ++if (des[i] == des[k+1]) {k++;}next[i] = k;} }
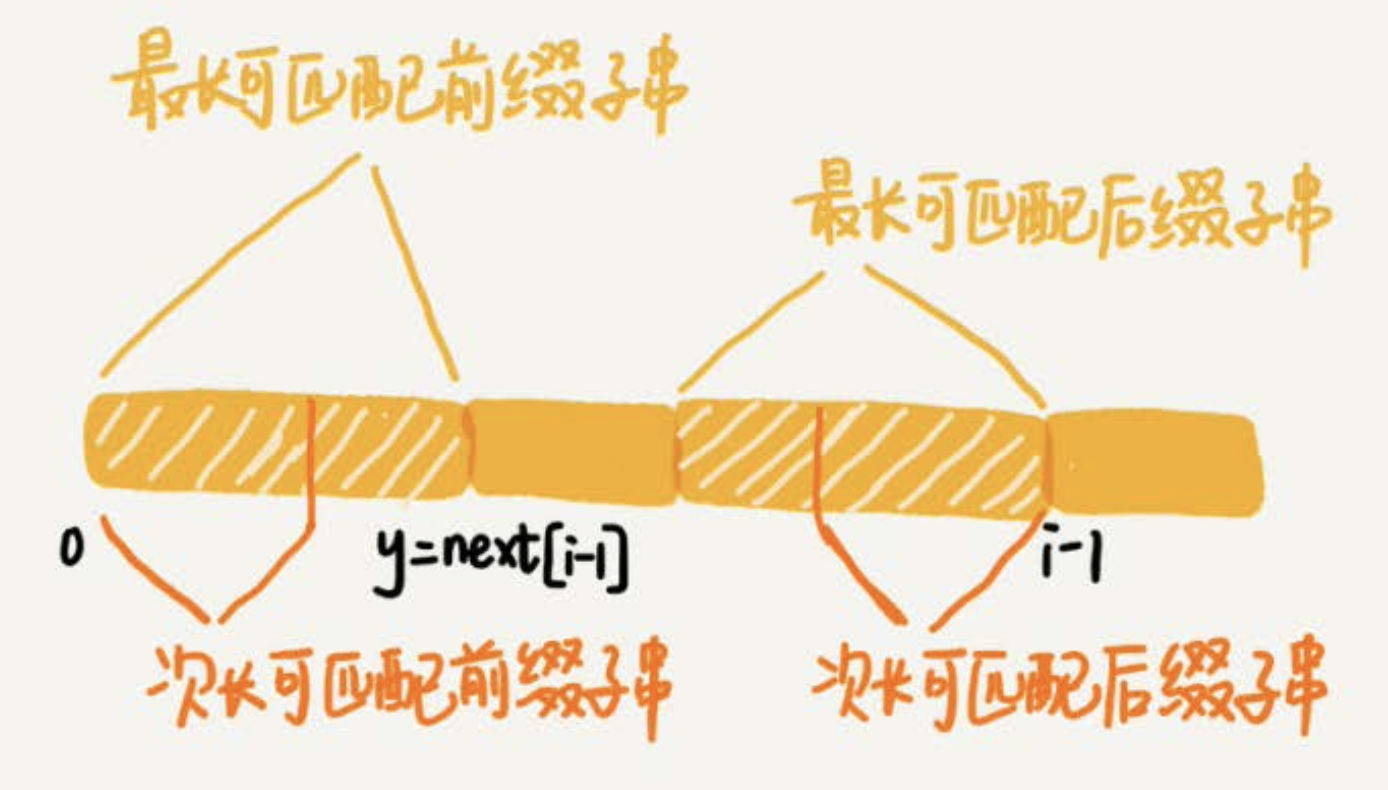
关于次长可匹配前缀和最长可匹配前缀之间的关系可以参考如下图理解一下:
y = next[i-1] 其实就是上面代码中的 k = next[k]的逻辑。
3.3 复杂度及完整代码
KMP算法以难理解著称,总体上就是一个回溯的过程,当前next[k]不满足匹配子串[0,k]的下一个字符相等时,则回到next[next[k]]看看。
空间复杂度:维护一个 m(模式串长度)大小的数组。
时间复杂度:
在next数组计算过程中,第一层for 循环[1,m-1],第二层的while循环中k=next[k]并不是每次都会执行,总的执行次数可以通过语句k++来判断,并不会超过m次,毕竟next[k]的回溯过程一定会碰到-1的情况。所以next数据计算过程整体的时间复杂度是O(m) – while循环的执行次数小于m,且不稳定,可以当作常量来看。
在外部主体进行匹配的过程中,外部循环[0,n-1],n表示主串的长度;因为j本身比i小, 所以while循环中 j=next[j-1]+1不可能循环n次,又因为next[j-1] 肯定小于j,相当于j之前的一个下标,也就是while中语句的执行次数是小于m的,也能够看作一个常量。
即外部匹配过程的时间复杂度是O(n)
所以总体的时间复杂度是O(m+n),当然相比于BM 的复杂度计算还不够严谨,像O(5n)也是O(n)的范畴,这个就比BM算法消耗时间更久了。
source code:
https://github.com/BaronStack/DATA_STRUCTURE/blob/master/string/kmp_alg.cc
完整代码如下:
#include <iostream>
#include <vector>
#include <string>using namespace std;void getNext(string des, vector<int> &next) {next[0] = -1;int k = -1;int i;// i begin with 1, next[0] always is -1for (i = 1; i< des.size(); i++) {// Find the longest match prefix by judge // two char dex[i] and des[k+1].// Just like case1 and case2: next[i-1]=k-1// if des[i] == des[k-1], then next[i] = next[i-1] + 1 = k;while(k != -1 && des[i] != des[k+1]) {//let 'k' storage 'next[next[...]]'k = next[k];}// find the match char, let k ++if (des[i] == des[k+1]) {k++;}next[i] = k;}
}int kmp_alg(string src, string des) {if (src.size() == 0 || des.size() <= 0) {return -1;}int src_len = src.size();int des_len = des.size();vector<int> next;int i, j;next.resize(des_len);// Get the next vectorgetNext(des,next);j = 0;for (i = 0;i < src_len; i++) {// 1. Find the bad char// 2. Next[j-1] is the longest match prefix's tail index// move the j to the destinations.// // Example:// i// 0 1 2 3 4 5 6 7 8 9// src: a b a b a e a b a c// des: a b a b a c d // 0 1 2 3 4 5 6// j//// when find bad char: i = 5, j = 5;// good prefix is : ababa// longest match prefix : aba// longest match prefix tail in des: 2// next[j-1] : next[5-1] = 2// j: 2 + 1 = 3//// after slide ,the src and des is bellow:// i// 0 1 2 3 4 5 6 7 8 9// src: a b a b a e a b a c// des: a b a b a c d // 0 1 2 3 4 5 6// j//while(j > 0 && src[i] != des[j]) {j = next[j-1] + 1; }// The good prefix, just add the jif (src[i] == des[j]) {j++;}// Match the des and return the index in srsif (j == des_len) {return (i - des_len + 1);}}return -1;
}int main() {string s1,s2;cin >> s1;cin >> s2;if (kmp_alg(s1,s2) == -1) {cout << s1 << " with " << s2 << " not match !" << endl;} else {cout << s1 << " with " << s2 << " match !" << endl;}return 0;
}
4. 总结
本节仅仅描述的是高效的单模式串匹配算法,也能够看到BM/KMP这样的复杂算法的设计,还是比较难以理解,尤其是KMP中用到了一些动态规划的思想。需要花费大量的时间和精力去思考实验,才能了解清楚内部的详细设计(从上周天开始研究,跟着极客时间的王争老师理解,差点怀疑自己智力是不是有问题,最后还是下班路上想明白细节。。。还是得尽可能多得思考训练,数据结构和算法功底决定未来技术壁垒的高度,尤其是现在搞的存储引擎,分布式存储/分布式数据库领域的核心,更是一点不能马虎),欢迎大家一起讨论。
后续将会深入多模式串的数据结构Tire树和算法AC自动机的设计,毕竟搜索引擎/文本编辑器中还是需要高效的多字符串的匹配才能满足实际生产环境的需求。
相关文章:

Java项目:中小医院信息管理系统(java+Springboot+ssm+mysql+maven+jsp)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:实现了挂号收费,门诊管理,划价收 费,药房取药,体检管理,药房管理,系统维护等各个模块功能&a…

DB2load遇到SQL3508N错误
SQL3508N装入或装入查询期间,当存取类型为 "<文件类型>" 的文件或路径时出错。原因码:"<原因码>"。路径:"<路径/ 文件>"。 [more]解释: 装入或装入查询处理期间,在尝…
【cocos2d-x 手游研发小技巧(3)Android界面分辨率适配方案】
先感叹一下吧~~android的各种分辨率各种适配虐我千百遍,每次新项目我依旧待它如初恋 每家公司都有自己项目工程适配的方案,这种东西就是没有最好,只有最适合!!! 这次新项目专项针对android,目的…
git submodule 使用场景汇总
文章目录1. 前言2. 基础命令介绍2.1 场景一:已有仓库,添加一个子模块2.2 场景二:已有仓库,添加一个子模块的特定分支2.3 场景三:已有仓库,更新子模块内容2.4 场景四:已有仓库,变更子…
Java项目:在线商城系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 前台展示后台管理,包括最基本的用户登录注册,下单, 购物车,购买,结算,订单查询,…

自定义参数解析器,减少10%的代码
*** 赋值调用方法* 如果为空,默认调用name()方法* 该方法必须是一个不含参数的方法,否则将会调用失败* @return*/value() : value用于绑定请求参数和方法参数名一致时的对应关系。比如user?statusNo=1。方法的参数写法如下:getUser(@EnumParam(value=“statusNo”) int status) 或者 getUser(@EnumParam() int statusNo)valueMethod() : 赋值时调用枚举中的方法。

微服务全做错了!谷歌提出新方法,成本直接降9倍!
一位DataDog的客户收到6500万美元的云监控账单的消息,也再次让业界无数人惊到了。事实上有些团队在将集中式单体应用拆分为微服务时,首先进行的往往不是建立领域模型,而只是按照业务功能将原来单体应用的一个软件包拆分成多个所谓的“微服务”软件包,而这些“微服务”内的代码高度耦合,逻辑边界不清晰,长期以来,不管大厂还是小厂,微服务都被认为是云原生服务应用程序架构的事实标准,然而2023,不止那位37signals的DHH决心下云,放弃微服务,就连亚马逊和谷歌等这些云巨头,正在带头开始革了微服务的命。

简述nodejs、npm及其模块在windows下的安装与配置
nodejs的安装 登陆官网http://nodejs.org/,自行安装,不需配置环境变量,安装中自动配置了。 检测是否安装成功,使用cmd输入 node -v 即可查看。 npm的安装 如果是最新版nodejs其实不用装npm,它集成了npm,验证…

discuz,ecshop的伪静态规则(apache+nginx)
discuz(nginx): (备注:该规则也适用于二级目录) rewrite ^([^\.]*)/topic-(.)\.html$ $1/portal.php?modtopic&topic$2 last; rewrite ^([^\.]*)/article-([0-9])-([0-9])\.html$ $1/portal.php?modview&aid$2&page$3 last; rewrite ^([^\.]*)/forum-…
字符串匹配数据结构 --Trie树 高效实现搜索词提示 / IDE自动补全
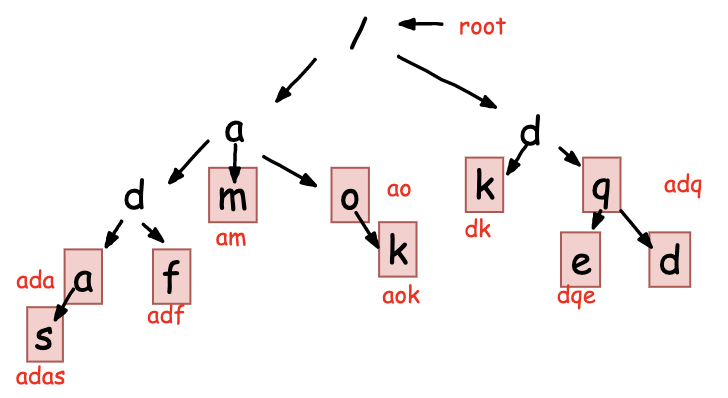
文章目录1. 算法背景2. Trie 树实现原理2.1 Trie 树的构建2.2 Trie树的查找2.3 Trie树的遍历2.4 Trie树的时间/空间复杂度2.5 Trie 树 Vs 散列表/红黑树3. Trie树的应用 -- 搜索词提示功能1. 算法背景 之前我们了解过单模式串匹配的相关高效算法 – BM/KMP,虽难以理…
Java项目:成绩管理系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 超豪华成绩管理系统,学生,教师,管理员三类用户集 成,课程表管理,成绩查询,成绩详情数据统计…

NSThread 多线程相关
1.下面的代码,有2点需要注意,1>就是 就是thread:所传得参数,这里传得的是nsarray 当然也可以传其他的类型。2> [self performSelectorOnMainThread:selector(update) withObject:nil waitUntilDone:YES]; 这个函数的作用是通知主线程进…

Windows Phone 8初学者开发—第19部分:设置RecordAudio.xaml页面
原文地址: http://channel9.msdn.com/Series/Windows-Phone-8-Development-for-Absolute-Beginners/Part-19-Setting-up-the-RecordAudioxaml-Page 系列地址: http://channel9.msdn.com/Series/Windows-Phone-8-Development-for-Absolute-Beginners 源代码: http://aka.ms/abs…

9.path Sum III(路径和 III)
Level: Easy 题目描述: You are given a binary tree in which each node contains an integer value. Find the number of paths that sum to a given value. The path does not need to start or end at the root or a leaf, but it must go downwards…
字符串匹配算法 -- AC自动机 基于Trie树的高效的敏感词过滤算法
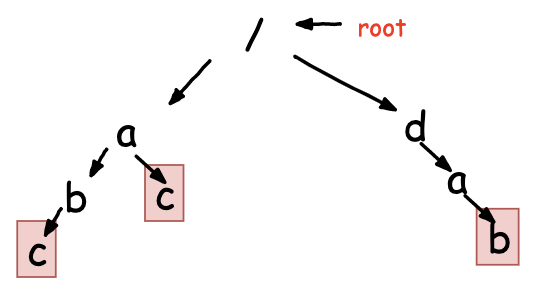
文章目录1. 算法背景2. AC自动机实现原理2.1 构建失败指针2.2 依赖失败指针过滤敏感词3. 复杂度及完整代码1. 算法背景 之前介绍过单模式串匹配的高效算法:BM和KMP 以及 基于多模式串的匹配数据结构Trie树。 1. BM和KMP 单模式串匹配算法细节 2. Trie树 多模式串的高效匹配数…
Java项目:仿小米商城系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 基于vue Springboot前后端分离项目精简版仿小米商城 系统,注册登录,首页展示,商品展示,商品购买,下单…

vb socket的使用
说明:原本在 csdn 博客 写博客的,因为使用的移动宽带,csdn的 博客无法访问,所以先暂时到博客园写博客了 有能解决移动宽带 有部分网站不能访问的问题,请联系我,QQ 809775607 /***************************/ 下面写wins…

不吹牛会死!国内音乐平台进入“大逃杀”
日前,一篇《看看海洋与腾讯音乐将如何“血洗”独立音乐应用》的文章引起了广泛关注。文中海洋声称长期独家签约的音乐及版权代理公司达40多家,占市场份额超过15%,一时间名不见经传的海洋音乐仿佛成了一匹跃然网上的“黑马”。然而据音乐圈深喉…

leetcode网学习笔记(1)
https://leetcode-cn.com/problems/reverse-linked-list/submissions/ 206 反转链表 错误原因:没有考虑到链表为空以及链表只有一个元素的情况 https://leetcode-cn.com/problems/swap-nodes-in-pairs/comments/ 24 两两交换链表 原方法:使用4个指针遍历…
贪心算法简单实践 -- 分糖果、钱币找零、最多区间覆盖、哈夫曼编解码
1. 贪心算法概览 贪心算法是一种算法思想。希望能够满足限制的情况下将期望值最大化。比如:Huffman编码,Dijkstra单源最短路径问题,Kruskal最小生成树 等问题都希望满足限制的情况下用最少的代价找到解决问题的办法。 这个办法就是贪心算法…

Java项目:个人博客系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:文章展示、热门文章、文章分类、标签云用户登录评论、匿名评论用户留言、匿名留言评论管理、文章发布、文章管理文章数据统计等等. 二、项目运行 环境…

第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器
第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器 原文:第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器 前言:在前一章已经演示了如何使用SSMS来配置资源调控器。但是作为DBA&a…

Android_开源框架_Volley实例
2019独角兽企业重金招聘Python工程师标准>>> 1.自定义相关类在 Android_开源框架_Volley(Google IO 2013)源代码及内部实现过程分析一文中,简单概述了Volley框架内部实现过程。如想理解彻底应该熟悉 android多线程通信机制( Android_Thread多线程_Handle…
maven的配置-2019-4-13
一.Maven的优点 1. 依赖管理 jar 包管理 2.一键构建 (编译-----测试------打包-----安装-----部署 ) 什么是项目构建? 指的是项目从编译-----测试------打包-----安装-----部署 整个过程都交给maven进行管理,这个过程称为构建 一…

WiredTiger引擎编译 及 LT_PREREQ(2.2.6)问题解决
近期需要为异构引擎做准备, wiredtiger 以其优异的性能(B-tree和LSM-tree都支持)和稳定性(Mongodb的默认存储引擎) 被我们备选为异构引擎里的一个子引擎,后续将深入wiredtiger 引擎原理。这里简单记录一下Wiredtiger 存储引擎的编译记录。 Environment …
Java项目:员工管理系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:分为前端翻后端部分,包括用户,区分晋通用户以及誉里员用户,包括首页展示,部门管理,人事管理,…

缺陷重点内容分析
1.缺陷优先级 序号优先级描述1低暂时不影响继续测试,可以在方便时解决2中部分功能测试无法继续测试;需要优先解决3高测试暂停,无法进行,必须立即解决2.缺陷的状态(图片来自云测视频) 3.缺陷生命周期与管理流…
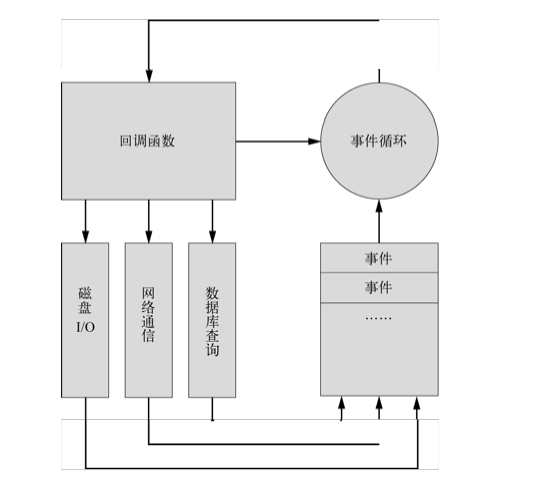
关于node.js的误会
昨天写了篇博客,介绍了一下我对node.js的第一次亲密接触后的感受,以为node.js很小众,出乎我意料很多人感兴趣,并且对博客中的细节问题做了评论,最多的是围绕node.js的异步与单线程展开的,当然还有很多关于n…
文本相关CSS
文本相关CSS 属性 word-breakoverflow-wrap(word-wrap)white-spacetext-overflowtext-wrap(目前主流浏览器都不支持)应用 一般断行需求实现文本不换行,以省略号表示超出的部分参考资料属性 word-break 作用:指定非CJK(中日韩)文本的断行规则。࿰…

Rocksdb 的优秀代码(三)-- 工业级 线程池实现分享
文章目录前言1. Rocksdb线程池概览2. Rocksdb 线程池实现2.1 基本数据结构2.2 线程池创建2.3 线程池 调度线程执行2.4 线程池销毁线程2.5 线程池优先级调度2.6 动态调整线程池 线程数目上限3. 总结前言 Rocksdb 作为一个第三方库的形态嵌入到各个存储系统之中存储元数据&#…
