字符串匹配算法 -- AC自动机 基于Trie树的高效的敏感词过滤算法
文章目录
- 1. 算法背景
- 2. AC自动机实现原理
- 2.1 构建失败指针
- 2.2 依赖失败指针过滤敏感词
- 3. 复杂度及完整代码
1. 算法背景
之前介绍过单模式串匹配的高效算法:BM和KMP 以及 基于多模式串的匹配数据结构Trie树。
1. BM和KMP 单模式串匹配算法细节
2. Trie树 多模式串的高效匹配数据结构
当有这样的需求:对于输入的主串,需要替换其中的敏感词为其他字符,也就是需要对trie树中的字符串逐个匹配,来判断该字符串是否在主串中,从而将其替换为制定字符。比如输出主串:abacdab , 使用Trie树构建的字符集如下:abc, ac,dab,最终替换的主串为: aba***** 。
如果用Trie树的匹配方式:
会拿着每一个trie树中的字符串 来和主串匹配,如果主串中没有这个字符串,则匹配trie树中的下一个字符串。
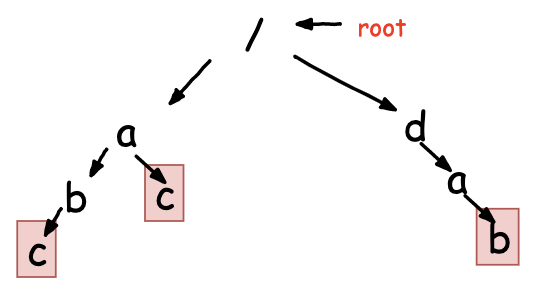
以root的26个字符为外层循环进行遍历,如果root->children_[des[i]-‘a’]不为空,则循环当前的trie树中的字符,且主串的i++,直到Trie树的叶子结点,发现当前trie树的这个字符串没法匹配,则从trie树的root重新开始匹配下一个trie树中的字符串。
基本的代码如下:
其中的AcNode也就是Trie-tree 中的TrieNode,下文的代码其实已经完成了Trie树的构建,相关的代码可以在开头的Trie树实现中查看。
// Match trie str with traditional method.
void matchLow(string des) {vector<pair<int,int>> match_vec;AcNode *tmp = root_;int des_len = des.size();int i = 0;// Traverse the des string which is user's inputwhile(i < des_len) {int index = des[i] - 'a';AcNode *p = tmp->children_[index];// Match every single str in trie treewhile(p != nullptr) {i ++;p = p->children_[des[i]-'a'];}if (p->isEndingChar_ == true) {int pos = i - p->length_ + 1;match_vec.push_back(make_pair(pos, p->length_));cout << "pos: " << pos << " len :" << tmp -> length_ << endl;} else {i++;}}
}
也就是每一个Trie树中的字符串都需要在主串中匹配一遍,这样的效率其实是比较低的。
有没有办法让在Trie树中的遍历跳过的字符更多一些呢?就像单模式串中KMP算法一样,让模式串在主串中的每一次移动尽可能多的位置,来降低匹配次数。kmp通过一个失效函数来达到这样的目的,同理Trie中也可以用一种算法,让主串尽可能多得匹配trie 树中的模式字符串,降低模式字符串的匹配次数,这个思想也就是AC自动机的算法思想,了解这个算法思想之前需要非常熟悉Trie树以及KMP算法的原理,文章开头有链接。
2. AC自动机实现原理
AC自动机全称Aho-Corasick 算法,实际原理就是在Trie树之上构建类似KMP的next数组,这里则是在Trie树上构建而已。
AcNode数据结构如下:
class AcNode {
public:char data_; // AcNode charbool isEndingChar_; // Ending posint length_; // Length of the stringAcNode *children_[26]; AcNode *fail; // fail pointer, to construct// the next array on Trie-treeAcNode(char data='/') :data_(data),isEndingChar_(false), length_(0){memset(children_, 0, sizeof(AcNode *)* 26);};
};
主要增加了一个失败指针,构建Ac自动机的过程 主要是将多个模式串构建成一个Trie树,并在其上构建失败指针(类似KMP的失效函数next数组)。
还是之前描述过的,AC自动机是为了减少模式串的匹配次数,每次Trie树中的模式串失配之后不需要从Trie的root节点重新开始匹配,而是跳转到下一个可能匹配的模式串的指定位置继续匹配,这个位置就是由失败指针来控制的。
举个例子:
一下Trie树为模式串构建的,包含字符串abcd, bcf, c
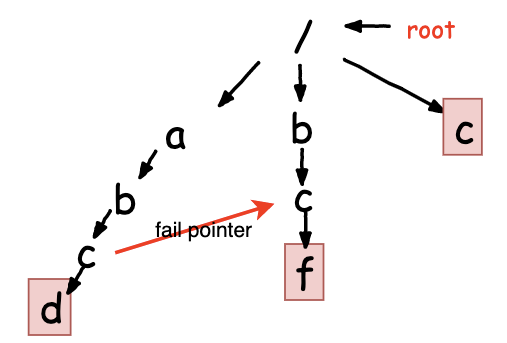
有一个从 从abcd字符串中C 指向bcf中的c 的指针,当我们在abcd中 d处匹配失效的时候可以继续从bcf 开始匹配,因为之前的bc已经在主串中存在了,所以不需要再从b开始进行匹配了。
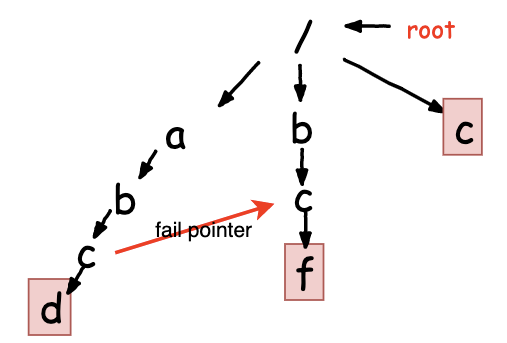
2.1 构建失败指针
前面的例子 能够对失败指针在Trie树中的匹配作用有一个整体的了解,会减少Trie树中的匹配次数。
注意,Ac自动机的场景是在一个主串中匹配多个模式串,一般用于敏感词过滤,匹配的过程就是减少在模式串中构成的Trie树的匹配次数。
在KMP算法构建失效函数的过程中提到了一个最长可匹配前缀子串,因为KMP是从左向右匹配,所以在遇到坏字符的时候每次模式串的滑动需要滑动大最长可匹配前缀子串的位置。这里也是类似的,可以看到如上例子: 模式串匹配到abcd的d字符时 发现和主串的f不匹配,这个时候c为失效指针起作用的位置,即在abc是已经和主串达成匹配的字符串了,只需要找到abc中的最长可匹配后缀子串即可。
后缀子串 就是最后一个字符串相同的子串,比如 abc 的后缀子串是 c, bc;最长可匹配后缀子串就是 Trie树中的其他字符串能够和bc匹配的前缀子串,比如案例中的bcf字符串 ,其前缀子串为b,bc ,则bc最长且和abc的后缀子串匹配。所以只需要让每一个失败指针保证指向的是最长可匹配后缀子串的结束位置即可。
可以像kmp算法那样,当我们要求某个节点的失败指针的时候,可以通过已经求得的、深度更小的节点的失败指针来推导,从而能够逐层求解每个节点的失败指针,也就是失败指针的构建会层次遍历Trie树。
构建失效指针的过程如下:
变更案例Trie树如下
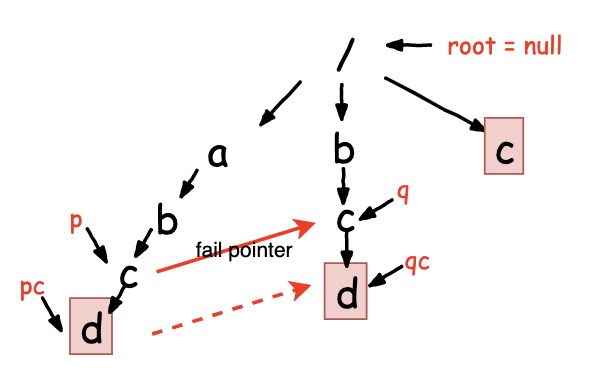
其中root节点的失败指针为null,假设我们知道了字符c对应的TrieNode p的失败指针为 q,那我们想要求p的子节点pc的失败指针。如果pc->data == qc->data,即p的子节点字符和q的子节点字符相同,则将节点pc的失败指针指向qc, pc->fail = qc
如果节点q没有子节点 或 q的子节点字符和pc的字符不想等,则让q = q->fail,再看看q的子字符是否和pc的字符相等,依次直到q==root,也就是找不到子节点和pc匹配的节点,就让pc->fail=root就好了。
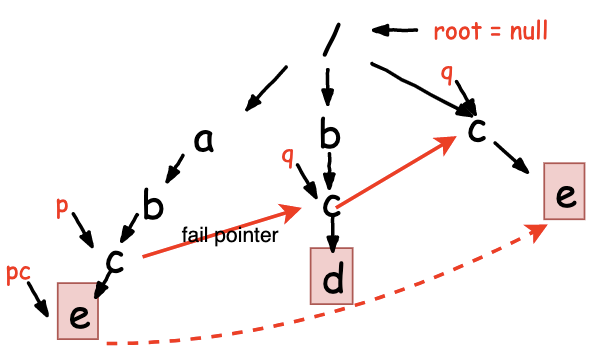
构建的过程需要层次遍历Trie树,依赖当前节点的上一个节点构建失败指针,将处于当前层的所有失败指针都构建完成。
// Build the fail pointer in trie node.
// The process is just like the next array in kmp alg.
void Trie::bfsBuildFailPointer() {queue<AcNode*> Q;// Init the root fail pointerroot_->fail = nullptr;Q.push(root_);while (!Q.empty()) {// Get the first element from queue, the element will be // removed laterAcNode *tmp = Q.front();Q.pop();// Build the fail pointer relationship with ervery children_for (int i = 0;i < 26; i++ ) {AcNode *pc = tmp->children_[i];if (pc == nullptr) {continue;}if (tmp == root_) {pc->fail = nullptr;} else {// Check the tmp's children_ pc and q's children_ qc// if they have the same char ,then pc -> fail = qc// Or, q while back to last fail pointerAcNode *q = tmp->fail;while(q != nullptr) {AcNode *qc = q->children_[pc->data_ - 'a'];if (qc != nullptr) {pc -> fail = qc;break;}// Let the fail pointer move forward// Until the q->data_ == qc -> data_//// Just like the getNext in kmp, k = next[k],// util you find the des[k+1] == des[i+1].// Then you can make sure you have find the best // prefix in current string.q = q->fail;}// qc's char is not equal with pc'c char in all q's fail pointer// keep pc's fail pointer to root_if (q == nullptr) {pc -> fail = root_;}}Q.push(pc);}}
}
2.2 依赖失败指针过滤敏感词
有了失败指针的完整位置,也就知道了能够快速匹配的捷径。
如下已经完成了所有节点失败指针构建的 Trie树
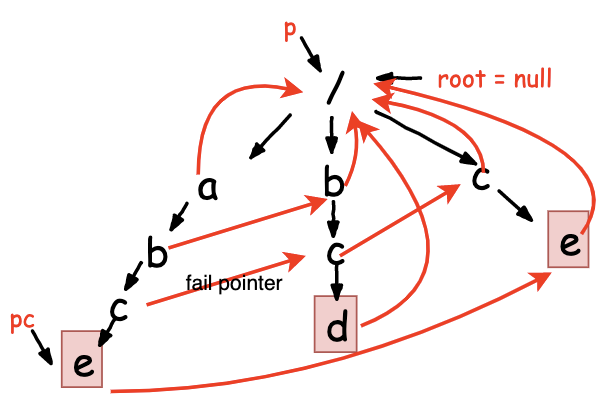
主串为 abcdhe
匹配过程中 输入的主串从 i=0开始,AC自动机从指针 p=root开始,假设主串是b
- case1: 如果p指向的节点 的一个子节点x的字符串 等于b[i],我们就更新p指向x。同时,通过其p的一系列失败指针,检查以失败指针为结尾的路径是否是模式串(是否是被打上了ending标记,这个标记是在构建trie树是标识每个模式串的结束)。处理完成之后,i++, 继续这两个过程。
- case2: 如果p 指向的节点没有等于b[i]字符的子节点,可以通过失败指针检查以该字符结尾的其他模式串是否有等于b[i]字符的子节点,并重复这两个过程。
abcdhe 为主串的匹配过程可以带入以上两个case, 非常容易理解。
以下逻辑为匹配模式串并输出 模式串在主串中的起始位置,并且完成模式串在主串中的替换:
// Match the des string with fail pointer
void Trie::match(string des) {AcNode *p = root_;int des_len = des.size();int i;vector<pair<int,int>> match_vec;for (i = 0;i < des_len; i++) {int index = des[i] - 'a';// case2: try to match the des[i],if failed,traverse// fail pointerwhile(p->children_[index] == nullptr && p != root_) {p = p->fail;}// find a char match with des[i]p = p->children_[index];if (p == nullptr) {p = root_;}AcNode *tmp = p;// Keep the tmp is not nullptr// case1: check the des[i]'s fail pointer ,if the fail pointer// is endingchar, and we will know that we have find a matching// string, record it.while(tmp != nullptr && tmp != root_) {if (tmp->isEndingChar_ == true) {int pos = i - tmp->length_ + 1;cout << "pos: " << pos << " len :" << tmp -> length_ << endl;match_vec.push_back(make_pair(pos, tmp->length_));}tmp = tmp -> fail;}}// Below is to output the replace result in with match str // in trie tree.if (match_vec.size() == 0) {cout << "string : " << des << " has no match str in trie tree!" << endl;return;}int j = 0;int tmp;i = match_vec[j].first;while(i < des_len && j < match_vec.size()) {tmp = match_vec[j].second;while(tmp --) {des[i++] = '*';}j++;}cout << "string : " << des << " match !" << endl;
}
3. 复杂度及完整代码
时间复杂度:
构建Trie树的时间复杂度是O(m*len),len表示敏感词的平均长度,m表示敏感词的个数
构建失败指针的复杂度:构建时 需要循环q = q->fail,这里每一次q指向的节点深度都会减1,也就是不会循环超过len次,。假设Trie树中总共k个节点,则每个节点构建失败指针的时间复杂度是O(len) ,总共O(k*len)次。
需要注意的是AC自动机会预先构建好,并不会频繁更新。
AC自动机匹配主串时的复杂度,
match函数中的两个while循环需要遍历当前节点的失败指针,时间复杂度为O(len),而外层的for循环时主串的长度,也就是O(n*len),因为敏感词其实都是一些短词语,实际上时间复杂度接近于O(n)。
空间复杂度的话,也就是之前说的Trie的内存消耗,本来也就很大,对于每一个节点都会消耗26个AcNode 的空间,这里有一些构建Trie树时的时间和空间消耗的Trad-off 优化。
完整代码:
https://github.com/BaronStack/DATA_STRUCTURE/blob/master/string/ac_alg.cc
总的来说,AC自动机在敏感词过滤的场景性能非常高效,但是由于Trie树带来的存储空间的消耗缺不可避免,不过整个算法实现思想还是非常有趣的。
相关文章:
Java项目:仿小米商城系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 基于vue Springboot前后端分离项目精简版仿小米商城 系统,注册登录,首页展示,商品展示,商品购买,下单…

vb socket的使用
说明:原本在 csdn 博客 写博客的,因为使用的移动宽带,csdn的 博客无法访问,所以先暂时到博客园写博客了 有能解决移动宽带 有部分网站不能访问的问题,请联系我,QQ 809775607 /***************************/ 下面写wins…

不吹牛会死!国内音乐平台进入“大逃杀”
日前,一篇《看看海洋与腾讯音乐将如何“血洗”独立音乐应用》的文章引起了广泛关注。文中海洋声称长期独家签约的音乐及版权代理公司达40多家,占市场份额超过15%,一时间名不见经传的海洋音乐仿佛成了一匹跃然网上的“黑马”。然而据音乐圈深喉…

leetcode网学习笔记(1)
https://leetcode-cn.com/problems/reverse-linked-list/submissions/ 206 反转链表 错误原因:没有考虑到链表为空以及链表只有一个元素的情况 https://leetcode-cn.com/problems/swap-nodes-in-pairs/comments/ 24 两两交换链表 原方法:使用4个指针遍历…
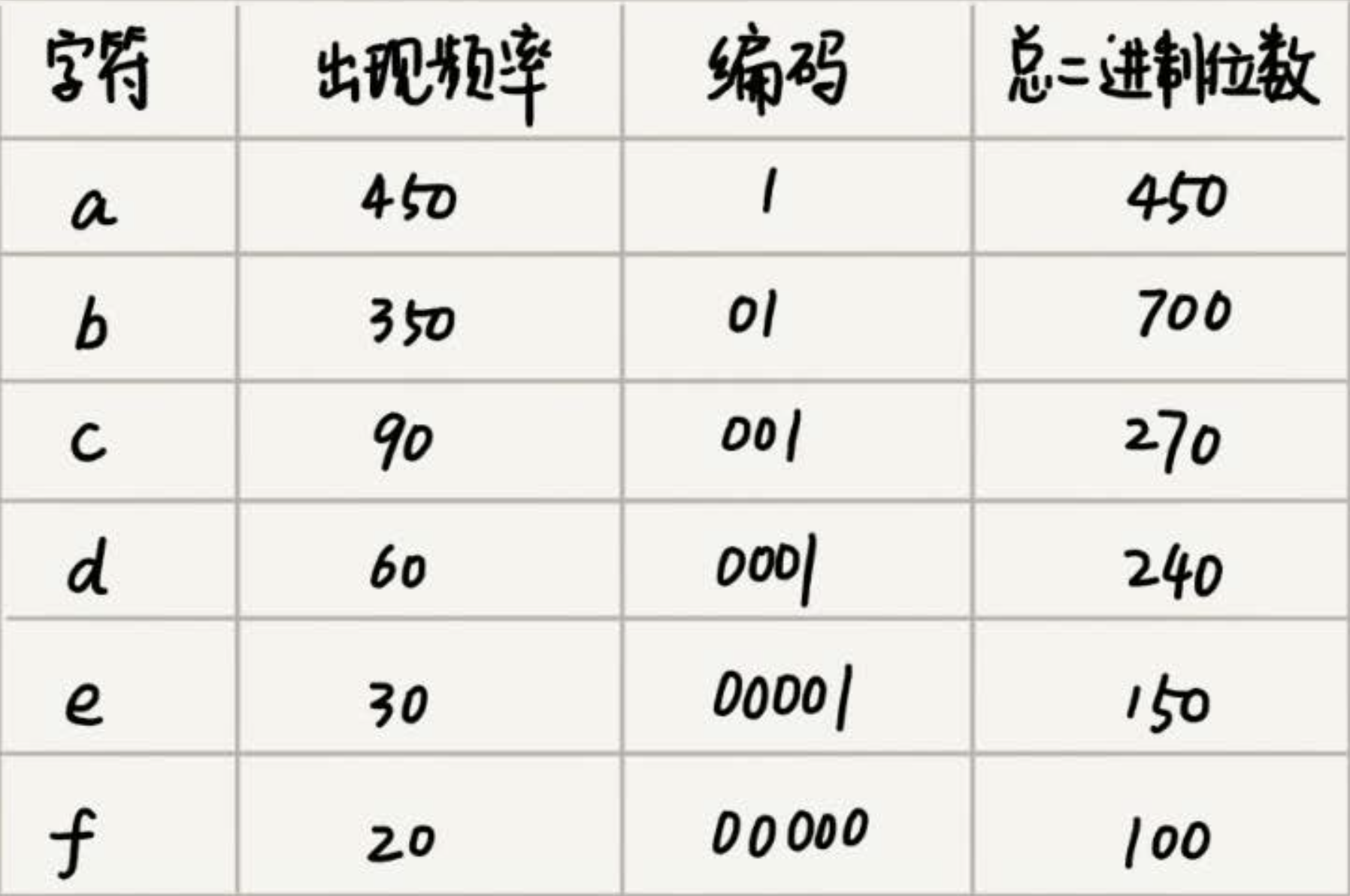
贪心算法简单实践 -- 分糖果、钱币找零、最多区间覆盖、哈夫曼编解码
1. 贪心算法概览 贪心算法是一种算法思想。希望能够满足限制的情况下将期望值最大化。比如:Huffman编码,Dijkstra单源最短路径问题,Kruskal最小生成树 等问题都希望满足限制的情况下用最少的代价找到解决问题的办法。 这个办法就是贪心算法…

Java项目:个人博客系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:文章展示、热门文章、文章分类、标签云用户登录评论、匿名评论用户留言、匿名留言评论管理、文章发布、文章管理文章数据统计等等. 二、项目运行 环境…

第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器
第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器 原文:第十九章——使用资源调控器管理资源(2)——使用T-SQL配置资源调控器 前言:在前一章已经演示了如何使用SSMS来配置资源调控器。但是作为DBA&a…

Android_开源框架_Volley实例
2019独角兽企业重金招聘Python工程师标准>>> 1.自定义相关类在 Android_开源框架_Volley(Google IO 2013)源代码及内部实现过程分析一文中,简单概述了Volley框架内部实现过程。如想理解彻底应该熟悉 android多线程通信机制( Android_Thread多线程_Handle…
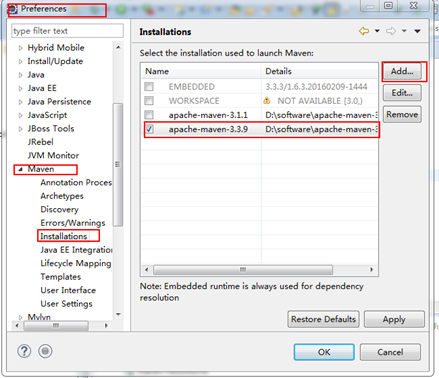
maven的配置-2019-4-13
一.Maven的优点 1. 依赖管理 jar 包管理 2.一键构建 (编译-----测试------打包-----安装-----部署 ) 什么是项目构建? 指的是项目从编译-----测试------打包-----安装-----部署 整个过程都交给maven进行管理,这个过程称为构建 一…

WiredTiger引擎编译 及 LT_PREREQ(2.2.6)问题解决
近期需要为异构引擎做准备, wiredtiger 以其优异的性能(B-tree和LSM-tree都支持)和稳定性(Mongodb的默认存储引擎) 被我们备选为异构引擎里的一个子引擎,后续将深入wiredtiger 引擎原理。这里简单记录一下Wiredtiger 存储引擎的编译记录。 Environment …
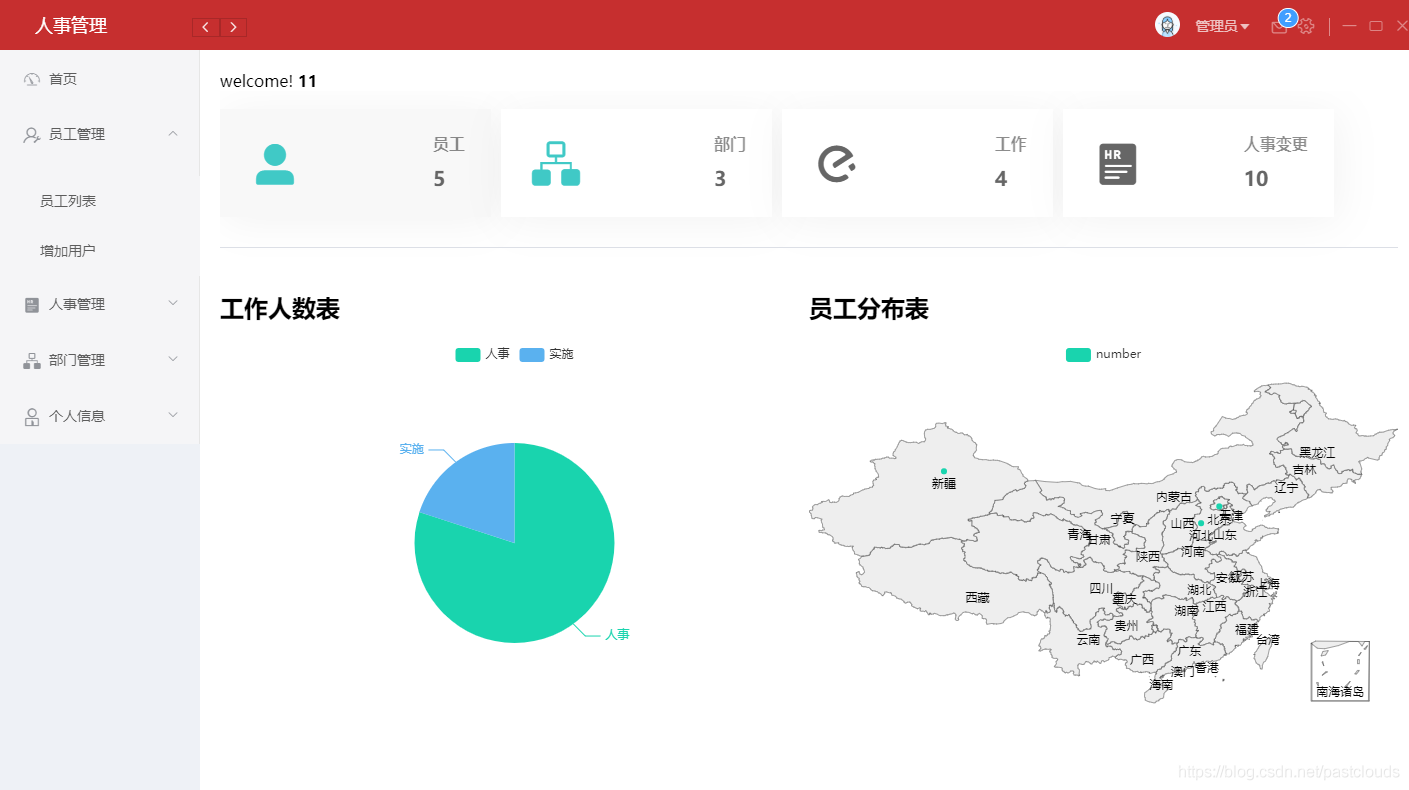
Java项目:员工管理系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括:分为前端翻后端部分,包括用户,区分晋通用户以及誉里员用户,包括首页展示,部门管理,人事管理,…

缺陷重点内容分析
1.缺陷优先级 序号优先级描述1低暂时不影响继续测试,可以在方便时解决2中部分功能测试无法继续测试;需要优先解决3高测试暂停,无法进行,必须立即解决2.缺陷的状态(图片来自云测视频) 3.缺陷生命周期与管理流…
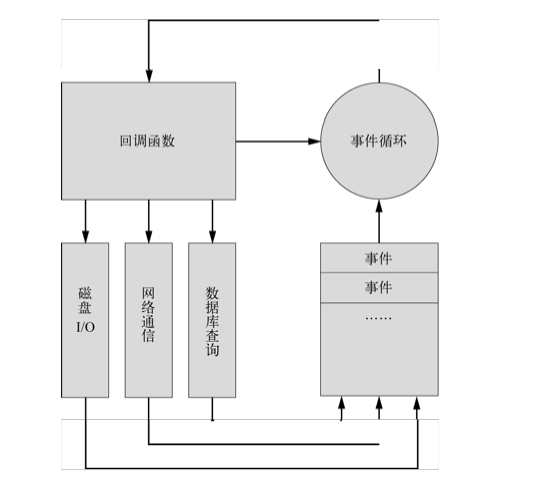
关于node.js的误会
昨天写了篇博客,介绍了一下我对node.js的第一次亲密接触后的感受,以为node.js很小众,出乎我意料很多人感兴趣,并且对博客中的细节问题做了评论,最多的是围绕node.js的异步与单线程展开的,当然还有很多关于n…
文本相关CSS
文本相关CSS 属性 word-breakoverflow-wrap(word-wrap)white-spacetext-overflowtext-wrap(目前主流浏览器都不支持)应用 一般断行需求实现文本不换行,以省略号表示超出的部分参考资料属性 word-break 作用:指定非CJK(中日韩)文本的断行规则。࿰…

Rocksdb 的优秀代码(三)-- 工业级 线程池实现分享
文章目录前言1. Rocksdb线程池概览2. Rocksdb 线程池实现2.1 基本数据结构2.2 线程池创建2.3 线程池 调度线程执行2.4 线程池销毁线程2.5 线程池优先级调度2.6 动态调整线程池 线程数目上限3. 总结前言 Rocksdb 作为一个第三方库的形态嵌入到各个存储系统之中存储元数据&#…
Java项目:网上电商项目(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 一款基于SpringbootVue的电商项目,前后端分离项目,前台后台都有,前台商品展示购买,购物车分类,订 单查…
3月7日 ArrayList集合
ArrayList与数组的区别: 数组是连续的、同一类型数据的一块区域,而集合可以是不连续的、多种数据类型的。 1.ArrayList ArrayList al new ArrayList(); al.Add(3); al.Add(5.09); al.Add("gfdg"); al.Inse…

什么时候出生好?
从年龄来说,女人头一胎的怀孕时间最好在35岁以前,因为过了35岁后不孕和头胎生育缺陷的比例会大幅度升高。那么,从孩子的角度,什么时候出生好?很多人不考虑这个问题,能不能怀上还难说那。迷信的人则追求出生…

数据库搜索与索引
索引是对数据库表中一列或多列的值进行排序的一种结构,使用索引可快速访问数据库表中的特定信息。如果想按特定职员的姓来查找他或她,则与在表中搜索所有的行相比,索引有助于更快地获取信息。 索引的一个主要目的就是加快检索表中数据&#x…
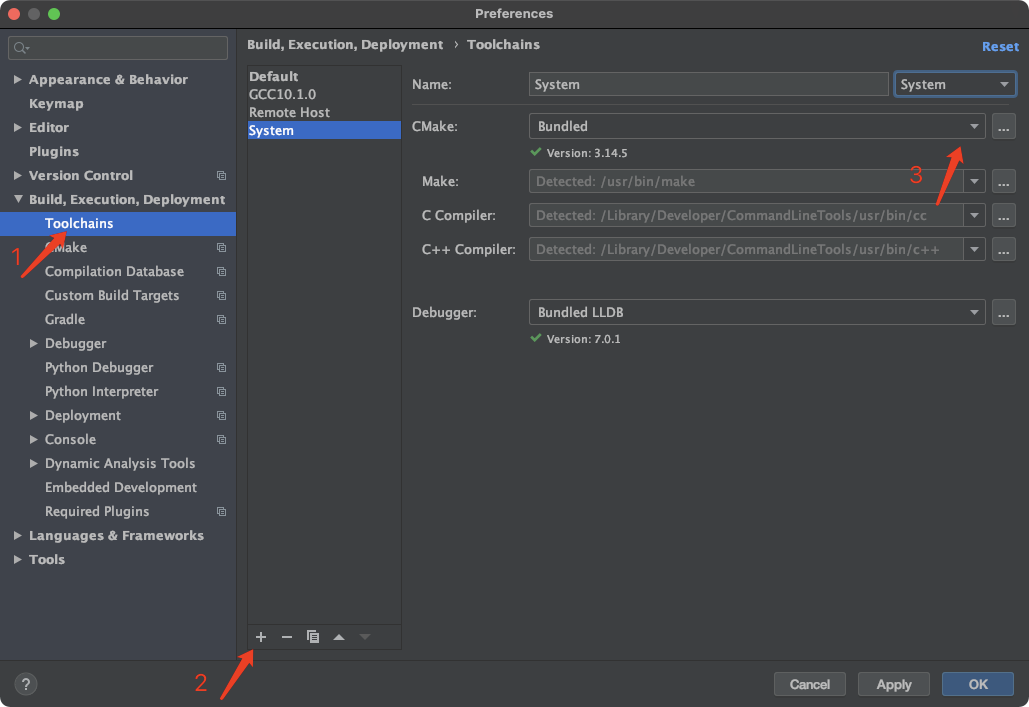
Clion 远程开发 配置
文章目录1. 增加远端服务工具2. 配置远端服务器3. 配置编译选项4. 设置远端开发路径Clion作为C/C语言友好的IDE,除了高效的代码索引 以及 基本的本地开发 能力之外还需要有远程开发能力,即我们工作中的代码处于远端linux服务器之上,通过在本地…
Java项目:朴素风个人博客系统(前后端分离+java+vue+Springboot+ssm+mysql+maven+redis)
源码获取:博客首页 "资源" 里下载! 一、项目简述 本系统功能包括: 基于vue Springboo痼J后端分离项目个人博客系统,注册 登录,首页展示,喜爰图书展示,后台图书维护,个人…

NodeJS+Mongodb+Express做CMS博客系统
楼主正在用业余时间开发中…… ,目前的版本仅支持会员系统,尝鲜一下吧~ hi-blog 一个 nodejsexpressmongodb 的 cms 系统怎么启动 默认你已经安装了 mongodb ;那么你得这样操作:安装项目 -> 初始化管理员 -> 运行项目 1、请…

Piranha实验总结
操作系统:rhel5.8分别在DirectorMaster和DirectorBackup上部署浮动资源(VIP IPVS策略)测试2个Director在DR模式下是否都可以正常工作。测试完成后都撤掉浮动资源。DirectorMaster[rootlocalhost ~]#yum install piranha[rootlocalhost ~]#piranha-passwdNew Passwor…

虚IP切换原理
高可用性HA(High Availability)指的是通过尽量缩短因日常维护操作(计划)和突发的系统崩溃(非计划)所导致的停机时间,以提高系统和应用的可用性。HA系统是目前企业防止核心计算机系统因故障停机的…
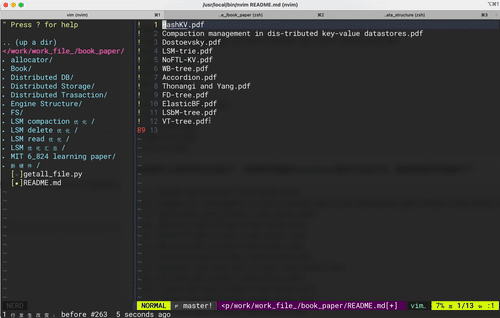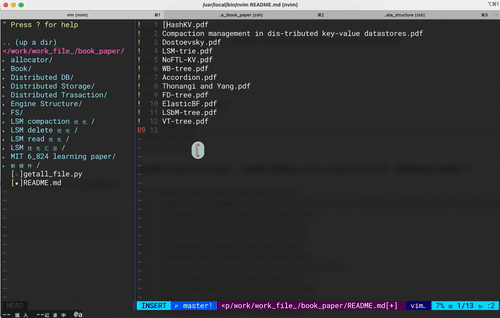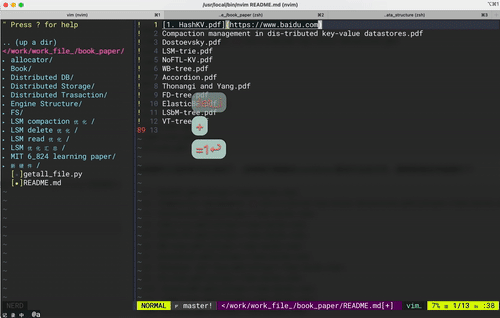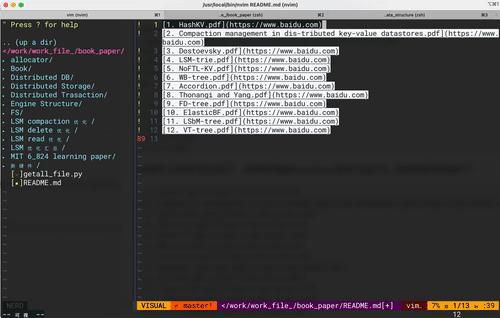
vim 键盘宏操作 -- 大道至简
最近利用vim做一些文本处理时 发现vim 支持的键盘宏是一个好东西啊,高效优雅得处理大量需要重复性操作的文本,让人爱不释手!!! 希望接下来对键盘宏的分享能够实际帮助到大家。 后文中描述的一些vim操作会汇集成指令字…
Java项目:家居购物商城系统(java+html+jdbc+mysql)
源码获取:博客首页 "资源" 里下载! 一、项目简述 功能: Java Web精品项目源码,家居商城分类展示,商品展示, 商品下单,购物车,个人中心,后台管理,用…

leetcode:Search in Rotated Sorted Array
题目要求: Suppose a sorted array is rotated at some pivot unknown to you beforehand. (i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2). You are given a target value to search. If found in the array return its index, otherwise return -1. You may a…

解决Debian-7.1下Chrome浏览器字体难看的问题
首先在 Advance Setting 的 font 标签页下做如下配置: 然后在用户目录下创建 .fonts.conf 文件,内容如下: <?xml version1.0?> <!DOCTYPE fontconfig SYSTEM fonts.dtd> <fontconfig><match target"font"&g…

HDU.4903.The only survival(组合 计数)
题目链接 惊了 \(Description\) 给定\(n,k,L\),表示,有一张\(n\)个点的无向完全图,每条边的边权在\([1,L]\)之间。求有多少张无向完全图满足,\(1\)到\(n\)的最短路为\(k\)。\(n,k\leq 12,\ L\leq10^9\)。 \(Solution\) 考虑暴力&a…

Rocksdb 写入数据后 GetApproximateSizes 获取的大小竟然为0?
项目开发中需要从引擎 获取一定范围的数据大小,用作打点上报,测试过程中竟然发现写入了一部分数据之后通过GetApproximateSizes 获取写入的key的范围时取出来的数据大小竟然为0。。。难道发现了一个bug?(欣喜) 因为写入的数据是…
