[树形dp] Jzoj P5233 概率博弈

Description

小A和小B在玩游戏。这个游戏是这样的：
有一棵n个点的以1为根的有根树，叶子有权值。假设有m个叶子，那么树上每个叶子的权值序列就是一个1->m 的排列。
一开始在1号点有一颗棋子。两人轮流将这颗棋子移向其当前位置的一个儿子。假如棋子到达叶子，游戏结束，最终获得的权值为所在叶子对应权值。
小A希望最后的权值尽量大，小B希望尽量小。小A是先手。
在玩了很多局游戏后，小B对其中绝大多数局游戏的结果不满意，他觉得是小A对叶子权值做了手脚。于是他一怒之下，决定将叶子的权值随机排列。现在小B想知道，假如叶子的权值是随机排列的（即叶子权值的每种排列都以等概率出现），那么游戏期望的结果是多少？
请输出答案乘上m! 对10^9+7取模的结果，显然这是一个整数。

Input

输入文件名为game.in。
第一行包含一个整数n。
接下来n-1行，每行两个整数u,v，表示有一条连接节点u,v的边。

Output

输出文件名为game.out。
输出一个整数，表示答案。

Sample Input

输入1：
5
1 2
2 3
1 4
2 5输入2：
10
10 7
7 6
10 2
2 3
3 8
3 1
6 9
7 5
1 4

Sample Output

输出1：
14输出2：
74

Data Constraint

对于10%的数据，n<=5
对于30%的数据，n<=10
对于60%的数据， n<=50
对于100%的数据，n<=5000,保证给出的是一棵合法的树。

题解

• 我们假设k为最后取的树，我们把一个叶子>=k染成1，把<k的染成0
• 考虑一下树形dp，设f[i][j][0/1]为以i为根的子树中有j个1当前点为0/1的方案数
• 那么对于当前是基层，也就是小A取值，f[i][j][0]= ∏f[son[x]][k][0]，f[i][j][1]=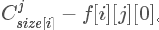。对于偶层，也就是小B取值也是一样的
• 枚举前面儿子的叶子然后枚举当前要合并的儿子的叶子背包一下
• 我们可以枚举k，也就是子树中1的个数，所以我们最后要记入答案是∑(f[1][k][1]-f[1][k+1][1])k! (size[1]-k)!

代码

#include <cstdio>
#define ll long long
using namespace std;
const ll N=5010,mo=1e9+7;
struct edge { int to,from; }e[N*2];
ll f[N][N][2],head[N],size[N],jc[N],g[N],ans,n,cnt,r;
void insert(int x,int y) { e[++cnt].to=y,e[cnt].from=head[x],head[x]=cnt; }
ll ksm(ll a,ll b){ for (r=1;b;b>>=1,a=a*a%mo) if (b&1) r=r*a%mo; return r;}
ll C(ll x,ll y) { return jc[y]*ksm(jc[y-x],mo-2)%mo*ksm(jc[x],mo-2)%mo; }
void dfs(int d,int x,int y,int l,int r)
{
    if (d>g[0]) { (f[x][r][l]+=y)%=mo; return; }
    for (int i=0;i<=size[g[d]];i++) if (f[g[d]][i][l]) dfs(d+1,x,y*f[g[d]][i][l]%mo,l,r+i);
}
void dp(int x,int y,int k)
{
    for (int i=head[x];i;i=e[i].from) if (e[i].to!=y) dp(e[i].to,x,k^1),size[x]+=size[e[i].to];
    g[0]=0; for (int i=head[x];i;i=e[i].from) if (e[i].to!=y) g[++g[0]]=e[i].to;
    if (size[x])
    {
        dfs(1,x,1,k,0);
        for (int i=0;i<=size[x];i++) f[x][i][k^1]=(C(i,size[x])-f[x][i][k]+mo)%mo;
    }
    else size[x]++,f[x][0][0]=f[x][1][1]=1;
}
int main()
{
    freopen("game.in","r",stdin),freopen("game.out","w",stdout),scanf("%lld",&n);
    for (int i=1,x,y;i<n;i++) scanf("%d%d",&x,&y),insert(x,y),insert(y,x);
    jc[0]=1; for (int i=1;i<=n;i++) jc[i]=jc[i-1]*i%mo; dp(1,0,0);
    for (int i=0;i<=size[1];i++) (ans+=f[1][i][1]*jc[i]%mo*jc[size[1]-i]%mo)%=mo;
    printf("%lld",ans);
}