线性代数-矩阵-【5】矩阵化简 C和C++实现

点击这里可以跳转至

【1】矩阵汇总：http://www.cnblogs.com/HongYi-Liang/p/7287369.html

【2】矩阵生成：http://www.cnblogs.com/HongYi-Liang/p/7275278.html

【3】矩阵加减：http://www.cnblogs.com/HongYi-Liang/p/7287403.html

【4】矩阵点乘：http://www.cnblogs.com/HongYi-Liang/p/7287324.html

【5】矩阵化简：现在的位置

（待续）

...

---

C++语言：

高斯消元法：

继续使用这个矩阵

当我们使用高斯消元（无回代）化简这个矩阵，是这样算的：

上述过程归纳为：

1. 找到第一行行的主元（第一行第一个数：1）
2. 消除第而三行的的第一个数（r2-2*r1;r3-4*r1）
3. 找到第二行的主元（第二行第二个数：-2）
4. 消除第三行的第二个数（r3-3/2*r2）

可以发现实际上是1和2两个步骤的循环，所以写成循环的形式

• 从第一行开始到最后一行

1. 找主元：找出第i的主元(第i行第i个数)
2. 消元：消除下面所有行的第i个数（下面每一行减去x倍的第一行来消除第i列）

到目前为止，基本达到消元的目的了，但是有一些小小的瑕疵

我们可能碰到一个这样矩阵，有一行全是0,例如这个：

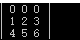
那么我们在步骤1中搜索到主元为0的话，0的任意倍数都是0，会导致第2步无法进行。所以我们需要添加换行的操作，计算方法为：

所以我们把代码逻辑修改成这样：

• 从第一行开始到最后一行

1. 找主元：找出第i的主元(第i行第i个数)，若主元为0，把第i行向下换行，直到找到有主元的行。若找不到主元，就开始找下一个
2. 消元：消除下面所有行的第i个数（下面每一行减去x倍的第一行来消除第i列）

下面就是高斯消元的主程序：

template <typename T>
bool Matrix<T>::GaussianElimination()
{Matrix<T> outputMatrix = *this;/*Gaussian elmiation*/for(int k=0;k<outputMatrix.m_iRows;k++){/*if all the pivot have been found*/if(k>=m_iColumns){break;}/*exchange rows downward to find the row's pivot*/for(int i=k+1;i<outputMatrix.m_iRows;i++){/*pivot is non-zero*/if(outputMatrix.m_vecMatrix[k][k] != 0){//T temp = outputMatrix.m_vecMatrix[0][0];break;}else{            if(i < outputMatrix.m_iRows){outputMatrix.exchangeRows(k,i);}}}/*if there is no pivot in this row*/if(outputMatrix.m_vecMatrix[k][k] == 0){break;}/*elimination:The rows below pivot row subtract times of pivot row*/for(int i=k+1;i<outputMatrix.m_iRows;i++){double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows if(RowsfirstData != 0) {outputMatrix.m_vecMatrix[i][k]=0;for(int j=k+1;j<outputMatrix.m_iColumns;j++){outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;}}}}*this = outputMatrix;return true;
}

高斯-若尔当法

若尔当在高斯消元的基础上加上了回代过程，把矩阵化简成行最简式。我们在高斯消元的基础上加上和回代，方法跟高斯消元相反，用上面的行减下面的行，这里就不详细描述（展开查看代码）

rref()//化简矩阵成行最简

template <typename T>
bool Matrix<T>::rref()
{Matrix<T> outputMatrix = *this;int rank=0;//the rank of the matrix, how many columns's pivot will it has(-1)/*Gaussian elmiation*/for(int k=0;k<outputMatrix.m_iRows;k++){/*if all the pivot elem have been found*/if(k>=m_iColumns){break;}/*exchange rows downward to find the pivot row*/for(int i=k+1;i<outputMatrix.m_iRows;i++){/*pivot is non-zero*/if(outputMatrix.m_vecMatrix[k][k] != 0){//T temp = outputMatrix.m_vecMatrix[0][0];rank++;break;}else{            if(i < outputMatrix.m_iRows){outputMatrix.exchangeRows(k,i);}}}/*if there is no pivot in this row*/if(outputMatrix.m_vecMatrix[k][k] == 0){break;}/*elimination:The rows below pivot row subtract times of pivot row*/for(int i=k+1;i<outputMatrix.m_iRows;i++){double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows if(RowsfirstData != 0) {outputMatrix.m_vecMatrix[i][k]=0;for(int j=k+1;j<outputMatrix.m_iColumns;j++){outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;}}}}/*normalizing:set all pivots to 1*/for(int i=0;i<outputMatrix.m_iRows;i++){for(int j=0;j<outputMatrix.m_iColumns;j++){if(outputMatrix.m_vecMatrix[i][j] !=0 )//pivot has been foound
            {double pivot = outputMatrix.m_vecMatrix[i][j];//get pivotfor(int k=i;k<outputMatrix.m_iColumns;k++){outputMatrix.m_vecMatrix[i][k] /=pivot;}break;}}}/*Back substitution*/for(int i = rank;i>=1;i--){/*find a first non-zero elem (It is pivot)*/for(int j=0;j<outputMatrix.m_iColumns;j++){double times=0;if(outputMatrix.m_vecMatrix[i][j] !=0)//pivot found
            {for(int l=i-1;l>=0;l--){times = outputMatrix.m_vecMatrix[l][j]/outputMatrix.m_vecMatrix[i][j]; for(int k=j;k<outputMatrix.m_iColumns;k++)//tims of this row subtract by each columns in upon row 
                    {outputMatrix.m_vecMatrix[l][k] -= times*outputMatrix.m_vecMatrix[i][k];}}break;}}}*this = outputMatrix;return true;
}

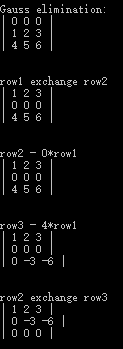
rrefmovie()//化简矩阵成行最简，并打印过程

template <typename T>
bool Matrix<T>::rrefmovie()
{Matrix<T> outputMatrix = *this;int rank=0;//the rank of the matrix, how many columns's pivot will it has(-1)/*Gauss elmiation*/cout<<"Gauss elimination:"<<endl;outputMatrix.printfAll();for(int k=0;k<outputMatrix.m_iRows;k++){/*If all the pivot elem have been found*/if(k>=m_iColumns){break;}/*Exchange rows downward to find the pivot row*/for(int i=k+1;i<outputMatrix.m_iRows;i++){/*Pivot is non-zero*/if(outputMatrix.m_vecMatrix[k][k] != 0){rank++;break;}else{            if(i < outputMatrix.m_iRows){outputMatrix.exchangeRows(k,i);}}if(k!=i){cout<<"row"<<k+1<<" exchange row"<<i+1<<endl;//Debug
                outputMatrix.printfAll();}}/*If there is no pivot in this row*/if(outputMatrix.m_vecMatrix[k][k] == 0){break;}/*Elimination:The rows below pivot row subtract times of pivot row*/for(int i=k+1;i<outputMatrix.m_iRows;i++){double RowsfirstData = outputMatrix.m_vecMatrix[i][k]/outputMatrix.m_vecMatrix[k][k];//Save the first data of next(k+1) rows if(RowsfirstData != 0) {outputMatrix.m_vecMatrix[i][k]=0;for(int j=k+1;j<outputMatrix.m_iColumns;j++){outputMatrix.m_vecMatrix[i][j] -= RowsfirstData*outputMatrix.m_vecMatrix[k][j] ;}}cout<<"row"<<i+1<<" - "<<RowsfirstData<<"*"<<"row"<<k+1<<endl;//Debug
            outputMatrix.printfAll();}}/*Normalizing:set all rows pivot to 1*/for(int i=0;i<outputMatrix.m_iRows;i++){for(int j=0;j<outputMatrix.m_iColumns;j++){if(outputMatrix.m_vecMatrix[i][j] !=0 )//pivot has been foound
            {double pivot = outputMatrix.m_vecMatrix[i][j];//get pivotfor(int k=i;k<outputMatrix.m_iColumns;k++){outputMatrix.m_vecMatrix[i][k] /=pivot;}cout<<"row"<<i+1<<" / "<<pivot<<endl;//DebugoutputMatrix.printfAll();//Debugbreak;}}}/*Back substitution*/cout<<"Back substitution:"<<endl;for(int i = rank;i>=1;i--){/*find a first non-zero elem (It is pivot)*/for(int j=0;j<outputMatrix.m_iColumns;j++){double times=0;if(outputMatrix.m_vecMatrix[i][j] !=0)//pivot found
            {for(int l=i-1;l>=0;l--){times = outputMatrix.m_vecMatrix[l][j]/outputMatrix.m_vecMatrix[i][j]; for(int k=j;k<outputMatrix.m_iColumns;k++)//tims of this row subtract by each columns in upon row 
                    {outputMatrix.m_vecMatrix[l][k] -= times*outputMatrix.m_vecMatrix[i][k];}cout<<"row"<<l+1<<" - "<<times<<"*"<<"row"<<i+1<<endl;outputMatrix.printfAll();}break;}}}*this = outputMatrix;return true;
}

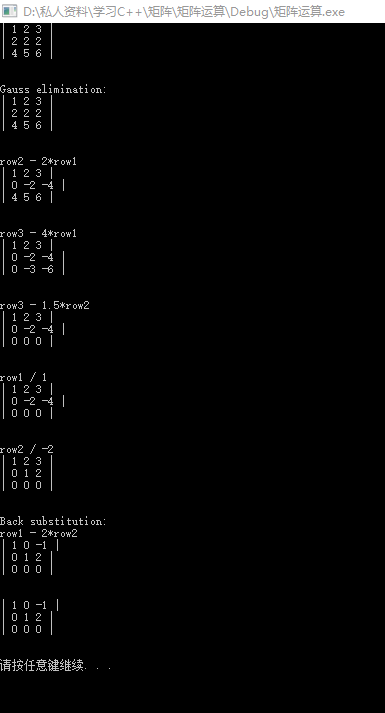
使用我们开始的矩阵测试：

    Matrix<double> matrix(3,3);matrix.setSpecifiedElem(0,0,1);matrix.setSpecifiedElem(0,1,2);matrix.setSpecifiedElem(0,2,3);matrix.setSpecifiedElem(1,0,2);matrix.setSpecifiedElem(1,1,2);matrix.setSpecifiedElem(1,2,2);matrix.setSpecifiedElem(2,0,4);matrix.setSpecifiedElem(2,1,5);matrix.setSpecifiedElem(2,2,6);matrix.printfAll();matrix.rrefmovie();matrix.printfAll();system("pause");

结果：