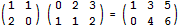4.1-1
返回只包含绝对值最小的元素的子数组。
4.1-2
Maximun-Subarray(A)max = -infinityfor i = 1 to A.lengthsum = 0for j = i to A.lengthsum = sum + A[i]if sum > maxmax = sumlow = ihigh = jreturn (low, high, max)
每次内循环都利用上次累加的结果,避免重复运算。外层循环执行n次,第i次外循环内层循环执行n-i+1次,所以总的时间复杂度为$\Theta (n^2)$。
4.1-3
这道题$n_0$的结果因人而异,我这里的结果是$n_0 = 63$。利用这种方法虽然可以改善总体的运行速度,但是不能够改变两种方法运行时间相同时输入规模的大小。
4.1-4
在算法的最后判断最大子数组的总和是否小于零,如果小于零则返回空子数组(empty subarray)。
4.1-5
算法的思想就是从前往后累加,如果当前子数组的累加和小于零,则意味着最大子数组(maximun subarray)肯定不包括该子数组,所以果断舍弃,重新开始累加。
Maximun-Subarray(A)max = 0, sum = 0, cur_low = 1for i = 1 to A.lengthsum = sum + A[i]if sum > maxmax = sumlow = cur_lowhigh = ielse if sum < 0cur_low = i + 1sum = 0if max > 0return (low, high, max)return NIL
4.2-1
突然发现这个算法算起来真够麻烦的。 $$S_1 = \{6\} \quad S_2=\{4\} \quad S_3=\{12\} \quad S_4=\{-2\} \quad S_5=\{6\}$$ $$S_6 = \{8\} \quad S_7=\{-2\} \quad S_8=\{6\} \quad S_9=\{-6\} \quad S_{10}=\{14\}$$ $$P_1 = \{6\} \quad P_2=\{8\} \quad P_3=\{72\} \quad P_4=\{-10\} \quad P_5=\{48\}\quad P_6=\{-12\}\quad P_7=\{-84\}$$ $$C_{11}=\{18\} \quad C_{12}=\{14\} \quad C_{21}=\{62\} \quad C_{22}=\{66\}$$
4.2-2
伪码还是比实际代码简单得多的,不用考虑一些中间存储的问题。
Strassen-Method(A, B)n = A.rowslet C be a new m*n matrixif n == 1c11 = a11 * b11elseS1 = B12 - B22S2 = A11 + A12S3 = A21 + A22S4 = B21 - B11S5 = A11 + A22S6 = B11 + B22S7 = A12 - A22S8 = B21 + B22S9 = A11 - A21S10 = B11 + B12P1 = Strassen-Method(A11, S1)P2 = Strassen-Method(S2, B22)P3 = Strassen-Method(S3, B11)P4 = Strassen-Method(A22, S4)P5 = Strassen-Method(S5, S6)P6 = Strassen-Method(S7, S8)P7 = Strassen-Method(S9, S10)C11 = P5 + P4 - P2 + P6C12 = P1 + P2C21 = P3 + P4C22 = P5 + P1 - P3 - P7return C
4.2-3
如果分割矩阵的时候矩阵的行数或列数为奇数,那么就把一个全零行或列补在矩阵上。最坏的情况下,每次分割都需要补行和列,所以递推公式变为 $$T(n)=7T(n/2 + 1)+\Theta((n+1)^2)=7T(n/2 + 1)+\Theta(n^2)$$ 可得最终时间复杂度保持不变,还是$\Theta (n^{\lg 7})$
4.2-4
利用这种方法的递推公式为 $$T(n)=kT(n/3)+\Theta(n^2)$$ 所以可以根据主方法(master method)算出k
- 如果$\log_3 k =2 \ \Rightarrow \ k=9$,那么满足第2种情况,$T(n)=\Theta (n^2 \lg n)=o(n^{\lg 7})$
- 如果$\log_3 k < 2 \ \Rightarrow \ k < 9$,那么满足第1种情况,$T(n)=\Theta (n^2)=o(n^{\lg 7})$
- 如果$\log_3 k > 2 \ \Rightarrow \ k > 9$,那么满足第3种情况,这时$\log_3 k < \lg 7 \Rightarrow k < 3^{\lg 7} \approx 21$
所以最大的k为21。
4.2-5
- 第一种情况下的复杂度递推公式为$T(n)=132464 T(n/68) + \Theta (n^2)$,$\log_{68} {132464} \approx 2.79512849$
- 第二种情况下的复杂度递推公式为$T(n)=143640 T(n/70) + \Theta (n^2)$,$\log_{70} {143640} \approx 2.79512269$
- 第二种情况下的复杂度递推公式为$T(n)=155424 T(n/72) + \Theta (n^2)$,$\log_{72} {155424} \approx 2.79514739$
所以三种情况都比Strassen的方法稍好,其中第二种方法最好。
4.2-6
分别将两个将矩阵拆分为k个$n \times n$矩阵,然后再利用Strassen方法计算n阶方阵乘法。 $$\begin{pmatrix} A_1 \\ A_2 \\ \vdots \\ A_k \end{pmatrix} \cdot \begin{pmatrix} B_1 & B_2 & \cdots & B_k \end{pmatrix} = \begin{pmatrix} A_1 B_1 & A_1 B_2 & \cdots & A_1 B_k \\ A_2 B_1 & A_2 B_2 & \cdots & A_2 B_k \\ \vdots & \vdots & \ddots & \vdots \\ A_k B_1 & A_k B_2 & \cdots & A_k B_k \end{pmatrix}$$ $$\begin{pmatrix} B_1 & B_2 & \cdots & B_k \end{pmatrix} \cdot \begin{pmatrix} A_1 \\ A_2 \\ \vdots \\ A_k \end{pmatrix} = \begin{pmatrix} A_1 B_1 + A_2 B_2 + \cdots + A_k B_k \end{pmatrix}$$
4.2-7
由于$(a+bi)(c+di) = (ac-bd) + (ad+bc)i$,需要4次乘法,为了节省一次乘法需要利用到之前计算的结果。可以发现$ad+bc=(a+b)(c+d)-ac-bd$,所以只需要计算3次乘法即可。
4.3-1
假定有$\forall m < n, T(m) \le cm^2$,代入递推式可得 $$\eqalign { T(n) & \le c(n-1)^2 + n \\ & = cn^2 + (1-2c)n + c \\ & \le cn^2 & (n > 0, c \ge 1)}$$
4.3-2
假定有$\forall m < n, T(m) \le c \lg m$,代入递推式可得 $$\eqalign { T(n) & \le c \lg {\lceil \frac n2 \rceil} + 1 \\ & \le c \lg {(\frac n2 +1)} + 1 \\ & = c \lg {(\frac{n}{2} \frac {n+2}{n})} + 1 \\ & = c \lg {n} -c + c \lg {\frac {n+2}{n}} + 1 \\ & \le c\lg n -c+c \lg {\frac53} + 1 & (n \ge 3) \\ & \le c \lg n & (c \ge \ (1-\lg {\frac 53})^{-1}) }$$ 或者,假定有$\forall m < n, T(m) \le c \lg {(m-d)}$,代入递推式可得 $$\eqalign { T(n) & \le c \lg {(\lceil \frac n2 \rceil - d)} + 1 \\ & \le c\lg {(\frac n2 -d+1)}+1 \\ & = c\lg {(n-2d+2)}-c+1 \\ & \le c \lg {(n-d)} & (c \ge 1, d \ge 2)}$$
4.3-3
假定有$\forall m < n, T(m) \ge c (m+d) \lg (m+d)$,代入递推式可得 $$\eqalign {T(n) & \ge 2c (\lfloor \frac n2 \rfloor +d) \lg {(\lfloor \frac n2 \rfloor + d)}+n \\ & \ge 2c(\frac n2 +d-1) \lg {(\frac n2 -1+d)} + n \\ & = 2c(\frac n2+d-1) (\lg (n-2+2d) -1)+n \\ & = cn\lg {(n-2+2d)}+(1-c)n+2c(d-1)\lg {(n-2+2d)+2c(d-1)} \\ & \ge cn\lg {(n+d)}}$$ 其中$2d-2 \ge d, 1-c \ge 0, d-1 \ge 0, c \ge 0 \Rightarrow 0 \le c \le 1, d \ge 2$
4.3-4
假定有$\forall m < n, T(m) \le cm\lg m + d$,代入递推式可得 $$\eqalign {T(n) & \le 2c \lfloor \frac n2 \rfloor \lg {\lfloor \frac n2 \rfloor} + 2d + n \\ & \le cn\lg {\frac n2} + n + 2d\\ & = cn\lg {n} - (c - 1)n + 2d \\ & \le cn \lg n + d}$$ 其中$(c-1)n + d \ge 0 \Rightarrow c \ge 1, d \le c-1$,为了保证$T(1)=1 \le c \cdot 1 \cdot \lg 1 + d = d$,所以$d \ge 1, c\ge d+1$
4.3-5
归并排序(merge sort)的时间复杂度递推公式为$T(n) = 2T(n/2) + n$,分别证明其上下界
假定有$\forall m < n, T(m) \le c m \lg m$,代入递推式可得 $$\eqalign { T(n) & \le 2c \frac n2 \lg {\frac n2} +n \\ & = cn\lg n -cn + n \\ & \le cn \lg n & (c \ge 1)}$$ 假定有$\forall m < n, T(m) \ge c m \lg m$,代入递推式可得 $$\eqalign { T(n) & \ge 2c \frac n2 \lg {\frac n2} +n \\ & = cn\lg n -cn + n \\ & \ge cn \lg n & (c \le 1)}$$
4.3-6
类似于4.3-3,假定有$\forall m < n, T(m) \le c (m-d) \lg {(m-d)}$,代入递推式可得 $$\eqalign {T(n) & \le 2c (\lfloor \frac n2 \rfloor +17-d) \lg {(\lfloor \frac n2 \rfloor + 17-d)}+n \\ & \le 2c(\frac n2 +18-d) \lg {(\frac n2 +18-d)} + n \\ & = 2c(\frac n2+18-d) (\lg (n+36-2d) -1)+n \\ & = cn\lg {(n+36-2d)}-(c-1)n-2c(d-18)\lg {(n+36-2d)-2c(d-18)} \\ & \le cn\lg {(n-d)}}$$ 其中$2d-36 \ge d, c-1 \ge 0, d-18 \ge 0 \Rightarrow c \ge 1, d \ge 36$
4.3-7
假定有$\forall m < n, T(m) \le c m^{\log_3 4}$,代入递推式可得 $$\eqalign { T(n) & \le 4c (\frac n3)^{\log_3 4} + n \\ & = cn^{\log_3 4} + n \\ & \ge cn^{\log_3 4} }$$ 证明失败,改变断言式为$\forall m < n, T(m) \le cm^{\log_3 4} - dm$,代入递推式可得 $$\eqalign { T(n) & \le 4c (\frac n3)^{\log_3 4}-\frac43 dn + n \\ & = cn^{\log_3 4}-dn -(\frac 13 d-1)n \\ & \le cn^{\log_3 4} -dn & (c \ge 0, d \ge 3)}$$ 得证。
4.3-8
这道题目有错误,递推式应该为$T(n)=4T(n/2)+n$
假定有$\forall m < n, T(m) \le cm^2$,代入递推式可得 $$\eqalign {T(n) & \le 4c (\frac n2)^2 + n \\ & = cn^2 + n \\ & \ge cn^2 }$$ 证明失败,改变断言式为$\forall m < n, T(m) \le cm^2-dm$,代入递推式可得 $$\eqalign {T(n) & \le 4c(\frac n2)^2 - 4d \frac n2 + n \\ & = cn^2 -dn-(d-1)n \\ & \le cn^2-dn &(c\ge0, d \ge 1)}$$ 得证。
4.3-9
令$m=\lg n$,得到$T(2^m)=3T(2^{m/2})+m$,再令$S(m)=T(2^m)$,得到$S(m)=3S(m/2)+m$,利用主方法(master method)可以求得$T(n)=T(2^m)=S(m)=O(m^{\lg 3})=O((\lg n)^{\lg 3})$。
4.4-1
第一层$n$,第二层$3/2n$,第三层$9/4n$,共$\lg n$层,最底层有$3^{\lg n}=n^{\lg 3}$个子过程,可得总时间 $$\eqalign {T(n) & =\sum_{i=0}^{\lg n -1} {(\frac 32)^in} + \Theta (n^{\lg 3}) \\ & = \frac {(3/2)^{\lg n}-1}{(3/2)-1}n + \Theta (n^{\lg 3}) \\ & = 2(n^{\lg {3/2}}-1)n + \Theta (n^{\lg 3}) \\ & < 2n^{\lg 3}+\Theta (n^{\lg 3}) \\ & = O(n^{\lg 3})}$$ 证明:假定有$\forall m < n, T(m) \le cm^{\lg 3}-dm$,代入递推式可得 $$\eqalign {T(n) & \le 3c (\frac n2)^{\lg 3} -3dn +n \\ & = cn^{\lg3} -d - (2d- 1)n \\ & \le cn^{\lg 3}-d & (c\ge 0, d\ge \frac 12)}$$
4.4-2
总时间为 $$\eqalign {T(n) & = \sum_{i=0}^{\lg n-1} {2^{-i}n}+\Theta (n^2) \\ & \le 2n + \Theta (n^2) \\ & = O(n^2)}$$ 证明:假定有$\forall m < n, T(m) \le cm^2$,代入递推式可得 $$\eqalign {T(n) &\le c(\frac n2)^2+n^2 \\ & = cn^2-(\frac 34c -1)n^2 \\ & \le cn^2 &(c\ge \frac 43)}$$
4.4-3
第一层$n$,第二层$2n+4 \times 2$,第三层$4n+4^2 \times (2+1)$,共$\lg n$层,最底层有$4^{\lg n}=n^2$个子过程,总时间为 $$\eqalign {T(n) & = \sum_{i=0}^{\lg n-1} {2^in} + \sum_{i=1}^{\lg n-1}{(4^i \sum_{j=0}^i{2^{1-j}})} + \Theta (n^2) \\ & \le \sum_{i=0}^{\lg n-1} {2^in} + \sum_{i=1}^{\lg n-1}{4^i4} + \Theta (n^2) \\ & = \frac {2^{\lg n}-1}{2-1}n +4\frac {4^{\lg n}-1}{4-1} + \Theta (n^2) \\ & \le n^2 + \frac 43n^2 + \Theta (n^2) \\ & = O(n^2) }$$ 证明:假定有$\forall m < n, T(m) \le cm^2-dm$,代入递推式可得 $$\eqalign {T(n) & \le 4c(\frac n2 + 2)^2 -4dn + n \\ & = cn^2+8cn+16c-4dn+n \\ & = cn^2-dn -(3d-8c)n+16c \\ & \le cn^2-dn}$$ 其中$(3d-8c-1)n-16c \ge 0 \Rightarrow c \ge 0, n > 0,d \ge \frac{16c+8cn+n}{3n}$
4.4-4
第i层总时间为$2^i(n-i)$,共n层,总时间为 $$\eqalign {T(n) & = \sum_{i=0}^n {2^i(n-i)} \\ & = \sum_{i=0}^n2^in - \sum_{i=1}^n i2^i \\ & = 2^{n+1}n - (2^{n+1}n-2^{n+1}-1) \\ & = 2^{n+1}+1 \\ & = O(2^n)}$$ 证明:假定有$\forall m < n, T(m) \le c2^m - d$,代入递推式可得 $$\eqalign {T(n) & \le 2c2^{n-1}-2d+1 \\ & = c2^n-d-(d-1) \\ & \le c2^n-d & (c\ge 0, d\ge 1)}$$
4.4-5
第一层$n$,第二层$(3/2)n-1$,第三层$(9/4)n-3-1/2$,最长的路径n层,由于该递归树不是满的,所以总时间小于满递归树 $$\eqalign {T(n) & \le \sum_{i=0}^n{(\frac 32)^in} \\ &= \frac {(3/2)^{n+1}-1}{3/2-1}n \\ & \le 2n(\frac 32)^{n+1} \\ & = O(n(\frac 32)^n)}$$ 证明:假定有$\forall m < n, T(m) \le cm(3/2)^m$,代入递推式可得 $$\eqalign {T(n) & \le c(n-1)(\frac 32)^{n-1} + c(\frac n2)(\frac 32)^{n/2} + n \\ & = cn(\frac 32)^n - \frac 12 cn(\frac 32)^{n-1}-c(\frac 32)^{n-1}+\frac 12 cn(\frac 32)^{n/2}+n \\ & = cn(\frac 32)^n -\frac 12cn(\frac 32)^{n/2}((\frac 32)^{n/2-1}-1)-(c(\frac 32)^{n-1}-n) \\ & \le cn(\frac 32)^n & (c \ge 1, n \ge 2)}$$
4.4-6
第一层$cn$,第二层$cn$,最短路径为$\log_3 n$层,所以总时间大于$\log_3 n$层的递归树 $$T(n) \ge \sum_{i=0}^{\log_3 n}{cn} = cn \log_3n = \Omega (n \lg n)$$
4.4-7
第一层$n$,第二层$2n-4 \le 4 \lfloor n/2 \rfloor \le 2n$,最长$\lg n$层,最短$\lg n - 1$层,所以总时间 $$\eqalign {T(n) & \le \sum_{i=0}^{\lg n-1}{2^i}cn +\Theta(n^2) \\ & \le cn^2 + \Theta(n^2) \\ & = O(n^2) }$$ $$\eqalign {T(n) & \ge \sum_{i=0}^{\lg n-2}{2^i}cn - \sum_{i=1}^{\lg n -2}{(c \sum_{j=0}^{i-1}{4^i2^{-j}})} +\Theta(n^2) \Theta(n^2) \\ & \ge c(n-1)^2-2c\sum_{i=1}^{\lg n-2}{4^i} +\Theta(n^2) \\ & \ge c(n-1)^2-\frac 32c(n-1)^2 + \Theta(n^2) \\ & = \Omega(n^2)}$$ 证明: 假定有$\forall m < n, T(m) \le dm^2 - bm$,代入递推式可得 $$\eqalign { T(n) & \le 4d\lfloor \frac n2 \rfloor^2 - 4b\frac n2 + cn \\ & = dn^2 - bn -(b-c)n \\ & \le dn^2-bn & (d \ge 0, b \ge c) }$$ 假定有$\forall m < n, T(m) \le dm^2 - bm$,代入递推式可得 $$\eqalign { T(n) & \ge 4d\lfloor \frac n2 \rfloor^2 +cn \\ & \ge 4d(\frac n2-1)^2+cn \\ & = dn^2-4dn+4d+cn \\ & \ge dn^2 }$$ 其中$cn+4d-4dn \ge 0 \Rightarrow n \ge 2, d \le \frac c2$
4.4-8
每一层都是$cn$,层数为$n/a$,所以 $$\eqalign {T(n) = \sum_{i=0}^{n/a} {cn} = \frac ca n^2 = \Theta(n^2)} $$
4.4-9
类似于4.4-7,每层都是$cn$,最多$\log_{\min (\frac1{\alpha}, \frac1{1-\alpha})} n$层,最少$\log_{\max (\frac1{\alpha}, \frac1{1-\alpha})} n$层,所以 $$T(n) \le cn log_{\min (\frac1{\alpha}, \frac1{1-\alpha})} n = O(n \lg n)$$ $$T(n) \ge cn log_{\max (\frac1{\alpha}, \frac1{1-\alpha})} n = \Omega(n \lg n)$$ 综上$T(n) = \Theta (n \lg n)$