鱼眼镜头及其标定
1. 鱼眼镜头特性与镜头分类
普通镜头和针孔相机在数学模型上可以等价对待,都是射影变换(Perspective transform);
鱼眼镜头受到水下斯涅耳窗口现象的启发,采用不同的投影方式,来得到极大的视场角;
鱼眼镜头常用的投影方式包括等距投影、等积投影、体视投影、正交投影等;
2. 鱼眼镜头与呈像相似性
对日常生活、甚至一些艺术创作、科学研究来说,保持像与物的相似是一件好事。偏离相似性,我们就说镜头有了畸变,大多数时候,我们并不希望镜头有畸变,甚至在设计镜头的时候,专门针对「偏离相似性」——也就是镜头畸变进行校正。不过在一些特殊的场合,我们也需要特意偏离物像的相似性,以求得其他方面的便利。
一个极好的例子是气象科学中,对天空云量的测量。在这个场景中,人们希望能够获得尽可能大的视野范围,最好是直接把整个天空一次性拍摄下来——这就要求镜头能够达到 180° 的视场角。容易想到,我们可以把天空和云看做分布于一个半径无穷大的球面上,也就是说,我们要把一个(半)球面的场景尽可能全地记录、拍摄下来。普通的超广角镜头难以完成这样的任务。

如图所示,面对半球场景,普通的超广角镜头只能记录中间的部分,越靠近边缘,透视变形越大。图中同样长度的红色箭头,靠近边缘的话,经过镜头成像之后就变得更长;对于极端接近边缘的物体,普通的广角镜头是无法成像记录的。这种情况下,追求「相似性」反而成为了障碍。
既然追求「相似性」的普通镜头难以胜任这样的任务场景,那么我们放弃相似性是不是就可以完成任务了呢?比如,对于靠近边缘的光线,我们不再要求他继续保持出射角与入射角相等,而是弯折一些,这样不就可以记录更大的视角范围了吗?而且物体的长度也不至于被拉伸得很厉害。
人们想到了水下的鱼。由于水的折射率比空气大,光线从空气进入水中,折射角比入射角更小,并且入射角越大,这个变小的程度也越大。这正好是我们所需要的特性。由于这个特性,使得水下的鱼在向上看的时候,能一眼看到整个水面上的这个半球形空间;这整个空间的影像,都被「扭曲」、「压缩」到了一个半顶角约为 48° 的锥形内。

空气-水界面处的光线折射与全反射)
在这个锥形空间内部,是来自水面上的空间的光线,在这个锥形外部,是来自水面下景色的反射。也就是说,在水下向上看,在一个圈之外,只能看到水底的景色;所有水面上的景色,都被压缩在一个圈内。这个圈,也叫「斯涅耳窗口(Snell’s window)」
3. 鱼眼镜头及投影方式
从数学上来说,普通的镜头成像相当于进行了一次射影变换。那么鱼眼镜头是一个什么变换呢?我们来看看,鱼眼镜头的变换,需要有什么样的特性。
3.1
**第一,视角要大。**或者说,对于某一个入射角,经过镜头之后射向成像面的出射角,一定是要小于入射角的。否则没办法在一个相对较小的范围内记录极大的视角。
**第二,最好这个变换有比较良好的性质。**什么叫「良好的性质」?比如说普通镜头对应的射影变换,就有良好的性质,经过射影变换后,很多几何特征能保持不变,直线还是直线、圆锥曲线还是圆锥曲线。我们希望鱼眼镜头对应的这个变换,也能够保持一些几何特征不变。比如,变换前后,圆还是圆;比如,变换前后,一块空间所占的立体角不变。
第三,最好这个变换的形式比较简单。简单的形式方便让人从成像中直接观测、推断,而不用经过复杂的运算才能看出拍的是个什么东西。
我们来看看,满足这三个条件的情况下,鱼眼镜头可以有什么样的变换形式(我们把这种变换叫做投影,Projection)。为了直观地感受不同投影方式带来的差异,我写了一个简单的图形渲染器。受到 WiKi Fisheye lens 中的场景启发,我设置了一个差不多的场景,是一个直筒型的管道,管道壁上有规则的颜色格子。在这个场景中用不同的投影方式去模拟鱼眼镜头拍摄的图像,以便让大家有一个直观的感受。

(模拟场景管道内,普通 14mm 超广角不同视角拍摄的效果)
斯涅耳窗投影,也就是真的去模仿水下鱼类向上看的时候的场景,我把这个投影方式叫做斯涅耳窗投影。用公式表达出射角和入射角之间的关系是 θ′=sin−1(sinθ/n),其中 θ 是入射角,θ′ 是出射角,n 是水的折射率。很显然,这种投影方式最大的视角不会超过 180°。这种投影方式没什么特别的用处,在这里也只是作为最初的起点。现实中我从来没见哪个鱼眼镜头是用这种投影方式的。

(斯涅耳窗投影效果)
3.2 投影函数
鱼眼相机按照一定的投影函数来设计,尽可能大的场景投影到有限的图像平面内。根据投影函数的不同,鱼眼相机的设计模型大致能被分为四种:等积投影模型、等距投影模型、体视投影模型、正交投影模型。下面的四种鱼眼相机的投影模型反映出了空间中的一点P是如何投影到球面上,然后到图像平面上成像的。
3.2.1 等积投影模型
等积投影(Equisolid angle,equal area),也叫等立体角投影。用公式表达物体成像后与画面中心的距离 r 与入射角 θ 之间的关系就是 r=2fsin(θ/2)。
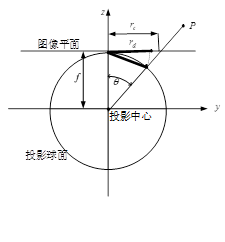
这种投影方式的特征在于,能保持变换前后,物体所占的立体角大小不变。或者说,在半球形空间中,半球面上两个「面积」相同的图案,成像后,在成像平面上的两个图案的面积仍然相同(虽然两者形状不一定相似)。这正是这个投影方式名字的由来。这种特性使得这个投影方式被广泛应用,其中一种场合就是测量全天云量覆盖情况。整个天空中云量覆盖多少,是由云所占的空间立体角的比例决定的。用这种投影方式的镜头,直接对着天空拍一张,在照片中测量一下云所占的像素面积比例,就得到了全天云量覆盖情况。在下图的模拟场景中,圆筒壁上每一列的各个小方格的面积都是相等的。

(等积投影效果)
3.2.2 等距投影模型
等距投影(Equidistance,linear scaled)。这种投影方式的特点是,物体在成像面上离开画面中心的距离,与物体在空间中离开光轴的角度成正比,这个比例系数就是镜头焦距。用公式表达这个距离与角度的关系就是 r=fθ,其中 r 就是物体的像到画面中心的距离,就是入射角,也等于物体在空间中离开光轴的角度。
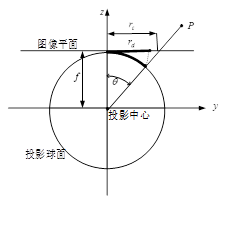
在这种投影变换下,物体离开中心的距离(角度)就是一个重要的几何性质,物体的空间角距离与物体的像在像平面上的平面距离,是成正比的。这也是这个投影方式名称的来源。这种方式的镜头较少,然而更多地用在军事领域。想像一下武器瞄准系统,使用这种投影方式的镜头,不仅监测的视野范围大,而且对于目标的方位角度,只要直接在画面里测量平面距离就可以了,非常方便。在下图的模拟场景中,中间一列的各个小方格的高度都是一样的。

(等距投影效果)
3.2.3 体视投影模型
体视投影(Stereographic,conform)。用公式表达就是 r=2ftan(θ/2),其中各个符号含义同前。这种投影方式的特点是能保持角度不变,这在数学上是一个非常良好的性质,叫做「保角变换(Conform)」
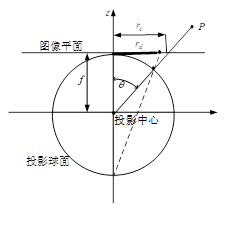
保持角度不变,意思是任何直线相交的角度,在变换之后是保持不变的(虽然直线本身可能变弯曲)。在保角变换下,一个圆仍然还是一个圆(直线可以看做直径无穷大的圆),所以在某种程度上,保角变换也是保持了「形状」不变的。在下面的模拟场景中,圆筒壁上的所有边界线,全部都变成了圆弧;所有线的交角,也都保持了 90° 不变。

(体视投影效果)
3.2.4 正交投影模型
正交投影(Orthographic)。这种投影方式,就像是把整个半球直接拍扁,用公式表达就是 r=sin(θ)。
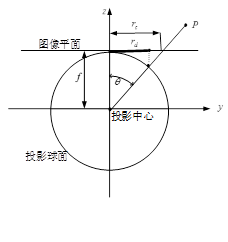
在几种投影方式中,这种投影方式带来的扭曲最大,对边缘物体压缩最厉害,实际很少使用。很显然,这种投影方式的最大视场角也不能大于 180°。

(正交投影效果)
在实际的商品化的民用镜头中,等积投影和等距投影都有不少使用,尤其在科研领域,相对的体视投影的镜头较少,不过也因为这种投影变形较小,还能保持角度不变,使得这种投影方式的镜头拥有相当多的爱好者
4. OpenCV中的鱼眼相机模型标定
OpenCV中使用的模型是由Kannala提出的一种鱼眼相机的一般近似模型。在等距投影模型的基础上提出来的。下面来详细分析其鱼眼相机模型的提出过程。我们可以将鱼眼相机模型的形式统一以等距投影模型的形式来表示,即
rd=fθdr_d=f θ_d rd=fθd
对实际的鱼眼镜头来说,它们不可能精确地按照投影模型来设计,所以为了方便鱼眼相机的标定,Kannala提出了一种鱼眼相机的一般多项式近似模型。通过前面的四个模型,可以发现 θdθ_dθd是θ的奇函数,而且将这些式子按泰勒级数展开,发现θdθ_dθd可以用θ 的奇次多项式表示,即
θd=k0θ+k1θ3+k2θ5+k3θ7+⋯θ_d=k_0θ+k_1θ^3+k_2θ^5+k_3θ^7+⋯ θd=k0θ+k1θ3+k2θ5+k3θ7+⋯
为了实际计算的方便,需要确定式中θdθ_dθd取到的次幂数。Kannala提出取式的前五项即取到的九次方,就给出了足够的自由度来很好地近似各种投影模型。 θdθ_dθd的一次项系数可以为1,于是OpenCV中使用的鱼眼相机模型为:
θd=k0θ+k1θ3+k2θ5+k3θ7+k4θ9⋯θ_d=k_0θ+k_1θ^3+k_2θ^5+k_3θ^7+k_4θ^9⋯ θd=k0θ+k1θ3+k2θ5+k3θ7+k4θ9⋯
上式表示的模型是根据四种鱼眼相机投影模型得出的一种通用鱼眼相机多项式模型。这种模型根据θ能够得到 θdθ_dθd,即通过无畸变图像中的点能够计算出鱼眼图像中的畸变点。这种模型在OpenCV的鱼眼相机标定方法中是适用的,因为OpenCV借助标定板对鱼眼相机进行标定。从空间点到鱼眼图像上的点的变换过程可用式子表示为:
[ Xc &Yc & Zc ] =RX+t
xc=Xc/Zc,yc=Yc/Zcr2=xc2+yc2θd=k0θ+k1θ3+k2θ5+k3θ7+k4θ9⋯xd=θd/r∗xc,yd=θd/r∗ycθ=arctan(r)u=fx∗xd+cxv=fy∗yd+cyx_c=X_c/Z_c, y_c=Y_c/Z_c \\ r_2={x_c}^2 + { y_c}^2 \\ θ_d=k_0θ+k_1θ^3+k_2θ^5+k_3θ^7+k_4θ^9⋯ \\ x_d=θ_d/r*x_c, y_d=θ_d/r*y_c \\ θ=arctan( r ) \\ u=f_x * x_d+c_x \\ v=f_y *y_d+c_y \\ xc=Xc/Zc,yc=Yc/Zcr2=xc2+yc2θd=k0θ+k1θ3+k2θ5+k3θ7+k4θ9⋯xd=θd/r∗xc,yd=θd/r∗ycθ=arctan(r)u=fx∗xd+cxv=fy∗yd+cy
上面式子中, X表示空间点,XcX_cXc表示相机坐标系下对应的空间点, R和t分别是两个坐标系之间的旋转矩阵和平移向量,(u,v)T(u,v)^T(u,v)T 表示投影到鱼眼图像上的对应点。
OpenCV中对鱼眼相机的标定步骤能够分成四步:
1.求内参矩阵的逆,由于摄像机坐标系的三维点到二维图像平面,需要乘以旋转矩阵R和内参矩阵K。那么反向投影回去则是二维图像坐标乘以 K*R的逆矩阵。
2.将目标图像中的每一个像素点坐标(j,i),乘以1中求出的逆矩阵iR,转换到摄像机坐标系(_x,_y,_w),并归一化得到z=1平面下的三维坐标(x,y,1)。
3.求出平面模型下像素点对应鱼眼半球模型下的极坐标(r, theta)。使用LM算法最小化定位的图像点和投影的图像点之间的投影误差;
4.利用鱼眼畸变模型求出拥有畸变时像素点对应的theta_d。
5.利用求出的theta_d值将三维坐标点重投影到二维图像平面得到(u,v),(u,v)即为目标图像对应的畸变图像中像素点坐标。
6.使用cv::Remap()函数,根据mapx,mapy取出对应坐标位置的像素值赋值给目标图像,一般采用双线性插值法,得到畸变校正后的目标图像。
标定代码:
链接: https://pan.baidu.com/s/1_-RruxBQ5DqDagB3JHYrMA?pwd=93mt 提取码: 93mt
5. 参考链接
[1] https://ieeexplore.ieee.org/document/1333993
[2] https://ieeexplore.ieee.org/document/1642666/citations#citations
[3] https://docs.opencv.org/4.x/db/d58/group__calib3d__fisheye.html
[4] https://blog.csdn.net/KYJL888/article/details/81043133
[5] https://blog.csdn.net/lwx309025167/article/details/103786550
[6] https://blog.csdn.net/u010128736/article/details/52864024/
[7] https://blog.csdn.net/qq_16137569/article/details/112398976
[8] https://blog.csdn.net/waeceo/article/details/51024396
[9] https://docs.opencv.org/3.0-beta/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html#fisheye-initundistortrectifymap
相关文章:
django -- url 的 name 属性
在html的form中使用给url定义的name值,可以在修改url时不用在修改form的src。 urls.py from django.conf.urls import url from mytest import viewsurlpatterns [# url(r^admin/, admin.site.urls),url(r^index/, views.index, namemysite), views.Index.as_view(…

两个矩形重叠部分面积
#include<stdio.h> #include<math.h> #define min(a,b) ( ((a)>(b)) ? (b):(a) ) #define max(a,b) ( ((a)>(b)) ? (a):(b) )typedef struct xy { int x; int y; }xy;void main() {xy a[4];int s,chang,kuang;while (true){printf("Please input 4 x,…

前百度面试官整理的——Java后端面试题(一)
2019独角兽企业重金招聘Python工程师标准>>> List 和 Set 的区别 List , Set 都是继承自 Collection 接口 List 特点:元素有放入顺序,元素可重复 , Set 特点:元素无放入顺序,元素不可重复,重复元…

vibe前景提取算法示例代码
//ViBe.h#pragma once #include <iostream> #include "opencv2/opencv.hpp"using namespace cv; using namespace std;#define NUM_SAMPLES 20 //每个像素点的样本个数 #define MIN_MATCHES 2 //#min指数 #define RADIUS 20 //Sqthere半径 #define SUBSAMPL…

Linux系统程序运行时加载动态库路径顺序
程序运行时加载动态库路径顺序(Linux) 在linux系统中,如果程序需要加载动态库,它会按照一定的顺序(优先级)去查找: 链接时路径(Link-time path)和运行时路径(Run-time path)不是一回…

浮动元素会引起的问题和你的解决办法
问题: (1)父元素的高度无法被撑开,影响与父元素同级的元素(2)与浮动元素同级的非浮动元素会跟随其后(3)若非第一个元素浮动,则该元素之前的元素也需要浮动,否…

Visual Paradigm 教程[UML]:如何使用刻板印象和标记值?(下)
下载Visual Paradigm最新试用版 已加入在线订购,现在抢购立享特别优惠>> 将构造型应用于模型元素 接下来,我们将构造型应用于模型元素。右键单击Customer,然后从弹出菜单中选择Stereotypes> External User。 从图形上看…

基于opencv的简单视频处理类示例
#include "opencv2/opencv.hpp" using namespace std; using namespace cv; class VideoProcessor { private: VideoCapture caputure; //图像处理函数指针 void (*process)(Mat &,Mat &); bool callIt; string WindowNameInput; string WindowNa…

flex数据绑定
2019独角兽企业重金招聘Python工程师标准>>> 1 、方法绑定 [Bindable(event"myFlagChanged")] private function isEnabled():String { if (myFlag)return true; else return ‘false; } <mx:TextArea id"myTA" text"{isEnabled()}&…

【error】error: field * has incomplete type
在编译程序是出现了如题错误, 类或结构体有前向声明的用法,编译到这里时还没有发现定义,不知道该类或者结构的内部成员,没有办法具体的构造一个对象,所以会报错。 两种解决方法: 方法一:将类成员…

Web前端学习笔记:Vue生命周期理解
一、感谢原创博主 示例代码出处vue2.0 探索之路——生命周期和钩子函数的一些理解 官方文档 二、生命周期简单描述 总共分为8个阶段创建前/后,载入前/后,更新前/后,销毁前/后。 创建前/后 在beforeCreated阶段,vue实例的挂载元素…

获取结构体中变量的偏移量
C/C获取结构体中变量的偏移量 1.某些特殊需求下,我们需要知道某个变量在其结构体中的偏移位置。 通常的做法就是定义一个宏变量,如下: #define OFFSET(structure, member) ((int64_t)&((structure*)0)->member) // 64位系统 #defin…

VS2010 CUDA 5.5 VA_X Win7 64位配置
一.安装CUDA5.5以及配置VS助手 1、安装之前必须确认自己电脑的GPU支持CUDA。在设备管理器中找到显示适配器(Display adapters),找到自己电脑的显卡型号,如果包含在http://www.nvidia.com/object/cuda_gpus.html的列表中,说明支持…

SmartRoute之大规模消息转发集群实现
为什么80%的码农都做不了架构师?>>> 消息转发的应用场景在现实中的应用非常普遍,我们常用的IM工具也是其中之一;现有很多云平台也提供了这种基础服务,可以让APP更容易集成相关功能而不必投入相应的开发成本。对于实现…

unity项目警告之 LF CRLF问题
unity中创建的脚本,以LF结尾。 Visual studio中创建的脚本,以 CRLF结尾。 当我们创建一个unity脚本后,再用VS打开编辑保存后,这个文件既有LF结尾符,也有CRLF结尾符。 解决办法:更改unity的代码生成模板&…
Eigen向量化内存对齐/Eigen的SSE兼容,内存分配/EIGEN_MAKE_ALIGNED_OPERATOR_NEW
1.总结 对于基本数据类型和自定义类型,我们需要用预编译指令来保证栈内存的对齐,用重写operator new的方式保证堆内存对齐。对于嵌套的自定义类型,申请栈内存时会自动保证其内部数据类型的对齐,而申请堆内存时仍然需要重写operat…

c/c++文件遍历
//CBrowseDir.h#pragma once#include <stdlib.h> #include <direct.h> #include <string.h> #include <io.h> #include <stdio.h> #include <iostream> using namespace std; class CBrowseDir { protected: //存放初始目录的绝对…

优化应用启动时的体验
2019独角兽企业重金招聘Python工程师标准>>> 对于应用的启动时间,只能是尽量的避免一些耗时的、非必要性的操作在主线程中,这样相对减少一部分启动的耗时,同时在等待第一帧显示的时间里,可以加入一些配置用来增加用户体…

系列四、SpringMVC响应数据和结果视图
2019独角兽企业重金招聘Python工程师标准>>> 项目结构如下 一、返回值分类 一 返回字符串 Controller方法返回字符串可以指定逻辑视图的名称,根据视图解析器为物理视图的地址,根据字符串最后跳转到对应jsp页面 第一步、导入依赖坐标文件、配置…
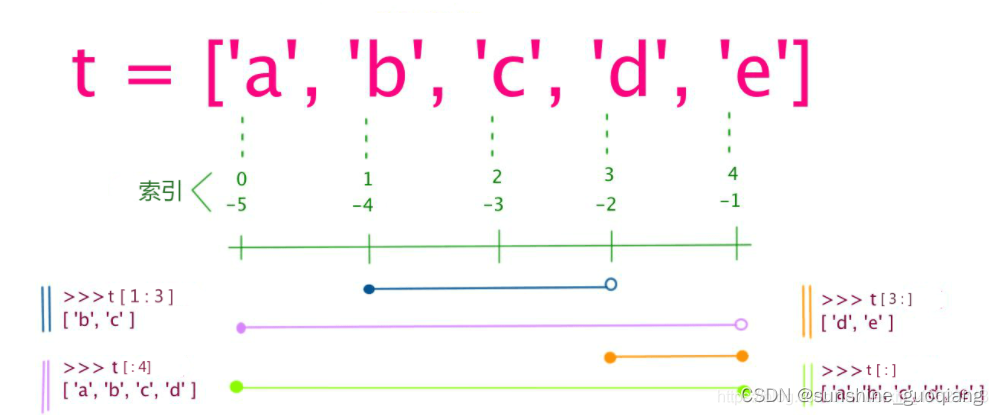
numpy数组切片:一维/二维/数组
文章目录numpy数组切片操作一维数组(冒号:)1、一个参数:a[i]2、两个参数:ba[i:j]3、三个参数:格式b a[i:j:s]4、例子二维数组(逗号,)取元素 X[n0,n1]切片 X[s0:e0,s1:e1…

行列式求值、矩阵求逆
#include <iostream> #include <string> #include <assert.h> #include <malloc.h> #include <iostream> #include <stdlib.h> #include <memory.h> #include <time.h>using namespace std;//动态分配大小位size的一维数组 te…

IP 地址子网划分
1.你所选择的子网掩码将会产生多少个子网2的x次方-2(x代表网络位借用主机的位数,即2进制为1的部分,现在的网络中,已经不需要-2,已经可以全部使用,不过需要加上相应的配置命令,例如CISCO路由器需要加上ip su…

git rebase 和 git merger
& git merge 在上图中,每一个绿框均代表一个commit。除了c1,每一个commit都有一条有向边指向它在当前branch当中的上一个commit。 图中的项目,在c2之后就开了另外一个branch,名为experiment。在此之后,master下的修…
matplotlib绘制三维轨迹图
1. 绘制基本三维曲线 # import necessary module from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt import numpy as np# load data from file # you can replace this using with open data1 np.loadtxt("./pos.txt") # print (data1) n…

求一个矩阵的最大子矩阵
#include <iostream> #include <string> #include <assert.h> #include <malloc.h> #include <iostream> #include <stdlib.h> #include <memory.h> #include <time.h> #include <limits.h>using namespace std;//动态分…

tcpdump抓包文件提取http附加资源
2019独角兽企业重金招聘Python工程师标准>>> 前面几篇文章铺垫了一大批的协议讲解,主要是为了提取pcap文件中http协议附加的资源。 1、解析pcap文件,分为文件格式头,后面就是数据包头和包数据了 2、分析每个包数据,数据…

smobiler介绍(二)
类似开发WinForm的方式,使用C#开发Android和IOS的移动应用?听起来感觉不可思议,那么Smobiler平台到底是如何实现的呢,这里给大家介绍一下。客户端Smobiler分为两种客户端,一种是开发版,一种是打包版开发版&…
Matplotlib基本用法
Matplotlib Matplotlib 是Python中类似 MATLAB 的绘图工具,熟悉 MATLAB 也可以很快的上手 Matplotlib。 1. 认识Matploblib 1.1 Figure 在任何绘图之前,我们需要一个Figure对象,可以理解成我们需要一张画板才能开始绘图。 import matplot…

HDU1201 18岁生日【日期计算】
18岁生日 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 32851 Accepted Submission(s): 10649Problem DescriptionGardon的18岁生日就要到了,他当然很开心,可是他突然想到一个问题&am…

TypeScript 从听说到入门(上篇)
我为什么会这样念念又不忘 / 你用什么牌的箭刺穿我心脏 我也久经沙场 / 戎马生涯 / 依然 / 被一箭刺伤 ——李荣浩《念念又不忘》 接下来我会分上、下两篇文章介绍 TypeScript。 我也是 TypeScript 初学者,这两篇文章是我的学习笔记,来源于一个系列的免费…
