数据结构与算法:12 数组与稀疏矩阵
12 数组与稀疏矩阵
知识结构:
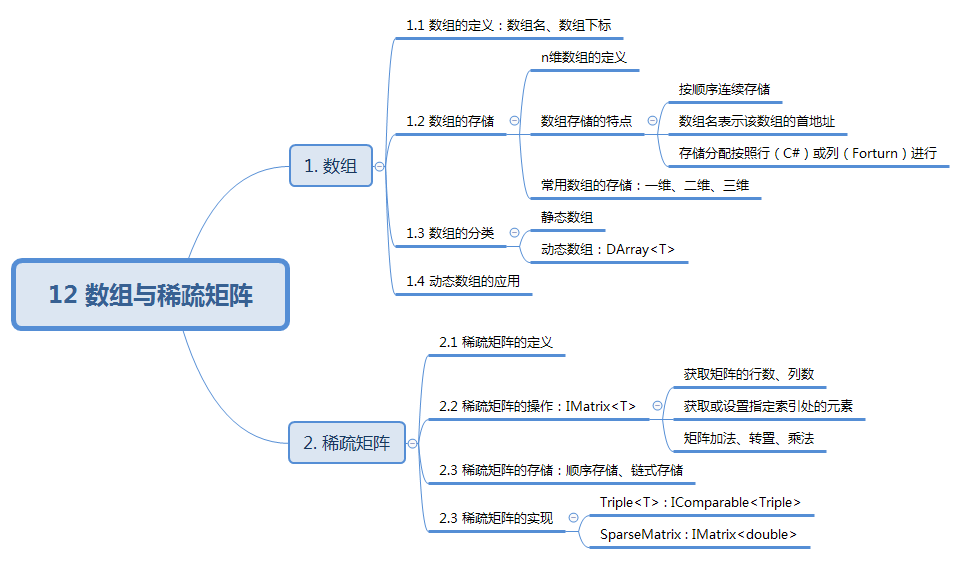
1. 数组
1.1 数组的定义
数组是具有一定顺序关系的若干对象组成的集合,组成数组的对象称为数组元素。
例如:
- 向量对应一维数组
A=(a0,a1,⋯,an−1)A=(a_0,a_1,\cdots,a_{n-1}) A=(a0,a1,⋯,an−1)
- 矩阵对应二维数组
Am×n=[a00a01⋯a0n−1a10a11⋯a1n−1⋯⋯⋯⋯am−10am−11⋯am−1n−1]A_{m \times n} =\begin{bmatrix} a_{00}&a_{01} &\cdots &a_{0n-1}\\ a_{10}&a_{11} &\cdots &a_{1n-1}\\ \cdots& \cdots &\cdots &\cdots\\ a_{m-10}&a_{m-11}& \cdots &a_{m-1n-1}\\ \end{bmatrix} Am×n=⎣⎢⎢⎡a00a10⋯am−10a01a11⋯am−11⋯⋯⋯⋯a0n−1a1n−1⋯am−1n−1⎦⎥⎥⎤
数组名表示群体的共性,即具有同一种数据类型;
下标表示个体的个性,即各自占有独立的单元。
1.2 数组的存储
(1)nnn维数组的定义
下标由nnn个数组成的数组称为nnn维数组。
例如:
//一维数组(线)
int[] a = new int[10]; //二维数组 (面)
int[ , ] a = new int[2,3];//三维数组 (体),类比:书(体)【2.页码 3.行 4.列】
int[ , , ] a = new int[2,3,4];
(2)数组存储的特点
- 数组元素在内存中按顺序连续存储。
- 数组的存储分配按照行(C、C++、C#等)或列(Forturn等)进行。
- 数组名表示该数组的首地址,是常量。
(3)常用数组的存储
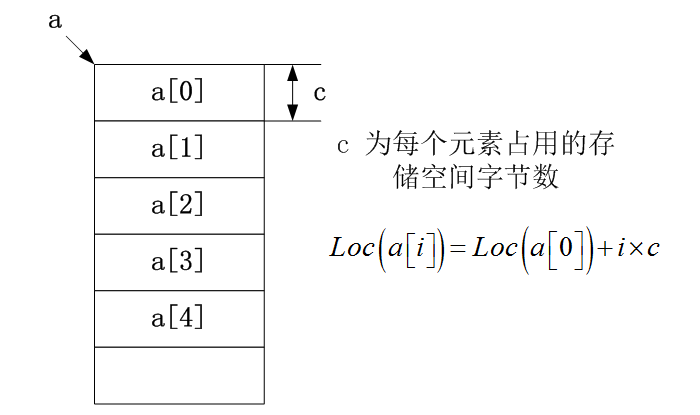
一维数组a[n]
各元素按下角标依次存放。
例:int[] a = new int[5];
二维数组a[m,n]
例:int[ , ] a = new int[2,3];

三维数组a[m,n,l]
第一维下标变化最慢,第三维(最后一维)下标变化最快。
例:int[ , , ] a = new int[2,3,4];
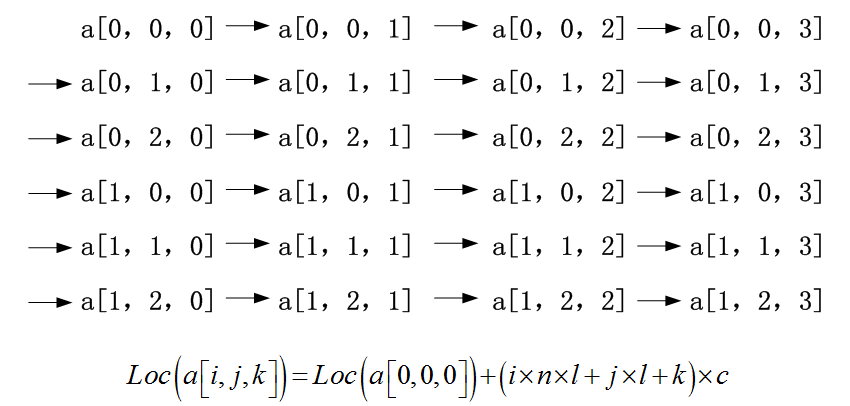
注意:
C#中int[,]与int[][]定义数组的区别
int[,]行数,列数确定
static void Main(string[] args)
{int[,] Arr = new int[2, 5] { { 1, 2, 3, 5, 6 }, { 1, 2, 3, 4, 5 } };for (int i = 0; i < 2; ++i){for (int j = 0; j < 5; ++j){Console.Write(Convert.ToString(Arr[i, j]) + " ");}Console.WriteLine();}// 1 2 3 5 6// 1 2 3 4 5
}
int[][]行数确定,列数不定
static void Main(string[] args)
{int[][] Arr = new int[3][]; //表示含有三个一维数组的数组Arr[0] = new int[5] { 1, 2, 3, 4, 5 };Arr[1] = new int[2] { 0, 1 };Arr[2] = new int[0] { };for (int i = 0; i < Arr.Length; ++i){foreach (int j in Arr[i]){Console.Write(j + " ");}Console.WriteLine();}// 1 2 3 4 5// 0 1//
}
1.3 数组的分类
数组可分为静态数组和动态数组两类。
(1)静态数组
在程序编译时分配空间的数组。
例:
//静态数组(声明之后数组长度不可改变)
int[] a = new int[10];
(2)动态数组
在程序运行时分配空间的数组(声明之后数组长度可根据问题而调整)。

using System;namespace LinearStruct
{/// <summary>/// 动态数组的抽象数据类型实现/// </summary>/// <typeparam name="T">动态数组中元素的类型</typeparam>public class DArray<T> where T : IComparable<T>{private T[] _array;/// <summary>/// 获取动态数组的当前长度/// </summary>public int Size { get; private set; }/// <summary>/// 初始化DArray类的新实例/// </summary>/// <param name="size">动态数组的初始长度</param>public DArray(int size){if (size <= 0)throw new ArgumentOutOfRangeException();Size = size;_array = new T[Size];}/// <summary>/// 改变动态数组的长度/// </summary>/// <param name="newSize">动态数组的新长度</param>public void ReSize(int newSize){if (newSize <= 0)throw new ArgumentOutOfRangeException();if (Size != newSize){T[] newArray = new T[newSize];int n = newSize < Size ? newSize : Size;for (int i = 0; i < n; i++){newArray[i] = _array[i];}_array = newArray;Size = newSize;}}/// <summary>/// 获取或设置指定索引处的元素/// </summary>/// <param name="index">要获得或设置的元素从零开始的索引</param>/// <returns>指定索引处的元素</returns>public T this[int index]{get{if (index < 0 || index > Size - 1)throw new IndexOutOfRangeException();return _array[index];}set{if (index < 0 || index > Size - 1)throw new IndexOutOfRangeException();_array[index] = value;}}}
}
1.4 动态数组的应用
编写一段代码,要求输入一个整数N,用动态数组A来存放2~N之间所有5或7的倍数,输出该数组。
例如:N=100
则输出:5 7 10 14 15 20 21 25 28 30 35 40 42 45 49 50 55 56 60 63 65 70 75 77 80 84 85 90 91 95 98 100
参考界面如下:

static void Main(string[] args)
{Console.WriteLine("N=");string s = Console.ReadLine();int n;if (int.TryParse(s, out n)){DArray<int> arr = new DArray<int>(10);int j = 0;for (int i = 2; i <= n; i++){if (i % 5 == 0 || i % 7 == 0){if (j == arr.Size)arr.ReSize(arr.Size + 10);arr[j] = i;j++;}}for (int i = 0; i < j; i++){Console.Write(arr[i] + " ");}}
}
2. 稀疏矩阵
2.1 稀疏矩阵的定义与操作
(1)稀疏矩阵的定义
若矩阵AAA中非零元素的个数远远小于零元素的个数,则称AAA为稀疏矩阵。
例:
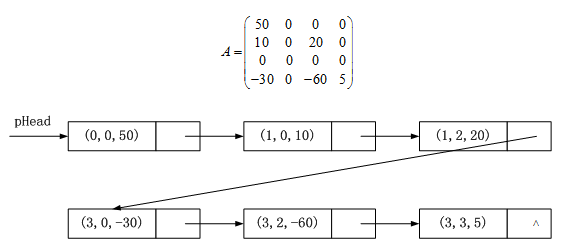
A=[500001002000000−300−605]A = \begin {bmatrix} 50 & 0 & 0 & 0\\ 10 & 0 & 20 & 0\\ 0 & 0 & 0 & 0\\ -30 & 0 & -60 & 5 \end{bmatrix} A=⎣⎢⎢⎡50100−3000000200−600005⎦⎥⎥⎤
若用二维数组存储,则太浪费存储空间。
(2)稀疏矩阵的操作
- 获取矩阵的行数
- 获取矩阵的列数
- 获取或设置指定索引处的元素
- 矩阵加法
- 矩阵转置
- 矩阵乘法

namespace LinearStruct
{/// <summary>/// 矩阵的抽象数据类型/// </summary>public interface IMatrix<T>{/// <summary>/// 获取矩阵的行数/// </summary>int Rows { get; }/// <summary>/// 获取矩阵的列数/// </summary>int Cols { get; }/// <summary>/// 获取或设置指定索引处的元素/// </summary>/// <param name="i">要获取或设置的元素从零开始的行索引</param>/// <param name="j">要获取或设置的元素从零开始的列索引</param>/// <returns></returns>T this[int i, int j] { get; set; }/// <summary>/// 矩阵加法/// </summary>/// <param name="b">与之相加的另一个矩阵</param>/// <returns>相加后的新矩阵</returns>IMatrix<T> Add(IMatrix<T> b);/// <summary>/// 矩阵转置/// </summary>/// <returns>转置后的新矩阵</returns>IMatrix<T> Transpose();/// <summary>/// 矩阵乘法/// </summary>/// <param name="b">与之右乘的另一个矩阵</param>/// <returns>相乘后的新矩阵</returns>IMatrix<T> Multiply(IMatrix<T> b);}
}
2.2 稀疏矩阵的存储与实现
可以利用(Row,Col,Value)的方式存储和定位稀疏矩阵中的非零元素,这种存储稀疏矩阵结点的方式称为三元组(Triple)。
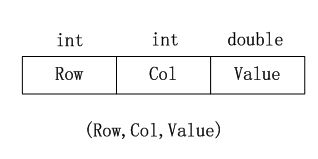
利用顺序的方式进行存储:

利用链式的方式进行存储:
(1)对结点的封装

using System;namespace LinearStruct
{/// <summary>/// 稀疏矩阵结点/// </summary>public class Triple : IComparable<Triple>{/// <summary>/// 获取结点所在矩阵中的行索引/// </summary>public int Row { get; }/// <summary>/// 获取结点所在矩阵中的列索引/// </summary>public int Col { get; }/// <summary>/// 获取或设置结点在矩阵中的值/// </summary>public double Value { get; set; }/// <summary>/// 初始化Triple类的新实例/// </summary>/// <param name="i">结点所在矩阵中的行索引</param>/// <param name="j">结点所在矩阵中的列索引</param>/// <param name="value">结点在矩阵中的值</param>public Triple(int i, int j, double value){if (i < 0 || j < 0)throw new Exception("数组元素位置无效.");Row = i;Col = j;Value = value;}/// <summary>/// Triple类的输出字符串/// </summary>/// <returns>Triple类的输出字符串</returns>public override string ToString(){return string.Format("({0},{1},{2})", Row, Col, Value);}/// <summary>/// 比较三元组中数据的大小/// </summary>/// <param name="other">被比较的三元组</param>/// <returns></returns>public int CompareTo(Triple other){if (Value < other.Value) return -1;if (Value > other.Value) return 1;return 0;}}
}
(2)对稀疏矩阵的封装
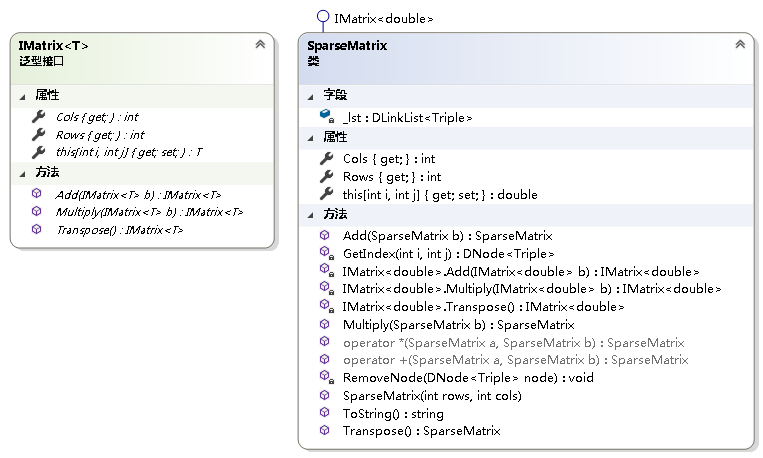
using System;namespace LinearStruct
{/// <summary>/// 矩阵抽象数据类型的实现--稀疏矩阵/// </summary>public class SparseMatrix : IMatrix<double>{private readonly DLinkList<Triple> _lst;/// <summary>/// 获取稀疏矩阵的行数/// </summary>public int Rows { get; }/// <summary>/// 获取稀疏矩阵的列数/// </summary>public int Cols { get; }/// <summary>/// 初始化SparseMatrix类的新实例/// </summary>/// <param name="rows">稀疏矩阵的行数</param>/// <param name="cols">稀疏矩阵的列数</param>public SparseMatrix(int rows, int cols){if (rows <= 0 || cols <= 0)throw new ArgumentOutOfRangeException();Rows = rows;Cols = cols;_lst = new DLinkList<Triple>();}private DNode<Triple> GetIndex(int i, int j){DNode<Triple> temp = _lst.PHead;while (temp != null){if (temp.Data.Row == i && temp.Data.Col == j)break;temp = temp.Next;}return temp;}private void RemoveNode(DNode<Triple> node){if (node.Next == null){_lst.Remove(_lst.Length - 1);}else if (node.Prior == null){_lst.Remove(0);}else{node.Prior.Next = node.Next;node.Next.Prior = node.Prior;}}/// <summary>/// 获取或设置指定索引处的元素/// </summary>/// <param name="i">要获取或设置的元素从零开始的行索引</param>/// <param name="j">要获取或设置的元素从零开始的列索引</param>/// <returns></returns>public double this[int i, int j]{get{if (i < 0 || i > Rows - 1 || j < 0 || j > Cols - 1)throw new IndexOutOfRangeException();DNode<Triple> node = GetIndex(i, j);return node == null ? 0.0 : node.Data.Value;}set{if (i < 0 || i > Rows - 1 || j < 0 || j > Cols - 1)throw new IndexOutOfRangeException();DNode<Triple> node = GetIndex(i, j);if (node == null){if (value != 0.0){_lst.InsertAtRear(new Triple(i, j, value));}}else{if (value != 0.0){node.Data.Value = value;}else{RemoveNode(node);}}}}/// <summary>/// 矩阵加法/// </summary>/// <param name="b">与之相加的另一个矩阵</param>/// <returns>相加后的新矩阵</returns>public SparseMatrix Add(SparseMatrix b){if (b == null)throw new ArgumentNullException();if (b.Rows != Rows || b.Cols != Cols)throw new Exception("两矩阵不能相加.");SparseMatrix temp = new SparseMatrix(Rows, Cols);for (int i = 0; i < Rows; i++)for (int j = 0; j < Cols; j++)temp[i, j] = this[i, j] + b[i, j];return temp;}/// <summary>/// 矩阵转置/// </summary>/// <returns>转置后的新矩阵</returns>public SparseMatrix Transpose(){SparseMatrix temp = new SparseMatrix(Cols, Rows);for (int i = 0; i < temp.Rows; i++)for (int j = 0; j < temp.Cols; j++)temp[i, j] = this[j, i];return temp;}/// <summary>/// 矩阵乘法/// </summary>/// <param name="b">与之右乘的另一个矩阵</param>/// <returns>相乘后的新矩阵</returns>public SparseMatrix Multiply(SparseMatrix b){if (b == null)throw new ArgumentNullException();if (Cols != b.Rows)throw new Exception("两矩阵不能相乘.");SparseMatrix temp = new SparseMatrix(Rows, b.Cols);for (int i = 0; i < Rows; i++){for (int j = 0; j < b.Cols; j++){double value = 0.0;for (int k = 0; k < Cols; k++)value += this[i, k] * b[k, j];temp[i, j] = value;}}return temp;}/// <summary>/// 矩阵加法运算/// </summary>/// <param name="a">第一个矩阵</param>/// <param name="b">第二个矩阵</param>/// <returns>相加后的新矩阵</returns>public static SparseMatrix operator +(SparseMatrix a, SparseMatrix b){if (a == null || b == null)throw new ArgumentNullException();return a.Add(b);}/// <summary>/// 矩阵乘法运算/// </summary>/// <param name="a">左边的矩阵</param>/// <param name="b">右边的矩阵</param>/// <returns>相乘后的新矩阵</returns>public static SparseMatrix operator *(SparseMatrix a, SparseMatrix b){if (a == null || b == null)throw new ArgumentNullException();return a.Multiply(b);}/// <summary>/// SparseMatrix类的输出字符串/// </summary>/// <returns>SparseMatrix类的输出字符串</returns>public override string ToString(){string str = string.Empty;DNode<Triple> temp = _lst.PHead;while (temp != null){str += temp.Data + "\n";temp = temp.Next;}return str;}IMatrix<double> IMatrix<double>.Add(IMatrix<double> b){return Add((SparseMatrix)b);}IMatrix<double> IMatrix<double>.Transpose(){return Transpose();}IMatrix<double> IMatrix<double>.Multiply(IMatrix<double> b){return Multiply((SparseMatrix)b);}}
}
举例:
static void Main(string[] args)
{IMatrix<double> a = new SparseMatrix(2, 3);IMatrix<double> b = new SparseMatrix(3, 2);SparseMatrix c = new SparseMatrix(2, 2);a[0, 2] = 1;a[1, 0] = 1;b[1, 1] = 4;b[2, 0] = 1;c[0, 1] = 1;c[1, 0] = 1;SparseMatrix d = (SparseMatrix)a * (SparseMatrix)b + c;IMatrix<double> e = a.Multiply(b).Add(c);Console.WriteLine("D:\n{0}", d);Console.WriteLine("E:\n{0}", e);// D:// (0, 0, 1)// (0, 1, 1)// (1, 0, 1)// E:// (0, 0, 1)// (0, 1, 1)// (1, 0, 1)
}

相关文章:

管理索引表:深入研究B树索引--重建,合并,删除(理论篇3)
重建索引 如果表中记录频繁地被删除或插入,尽管表中的记录总量保持不变,索引空间的使用量会不断增加。虽然记录从索引中被删除,但是该记录索引项的使用空间不能被重新使用。因此,如果表变化不定,索引空间量会不断增…

模块架构不是软件成功的“决定因素”
【本文是09年的一篇旧文,出于某些原因,对原文内容有删减,在这里整理后重新发表】 前言感谢XXX对我们技术,对我们公司产品提出这些意见,我们公司卖的是软件产品,开发软件是一件技术活,说实话&…
JavaScript面向对象修改标签页详解
双击标签页组件中的li小标签或者section 中的文本,可以对文本进行编辑。为了实现这个功能,需要先给li和section元素绑定双击事件,当双击文本后,将文本改成一个文本框,用来输入新的内容,在文本框中显示原来的…
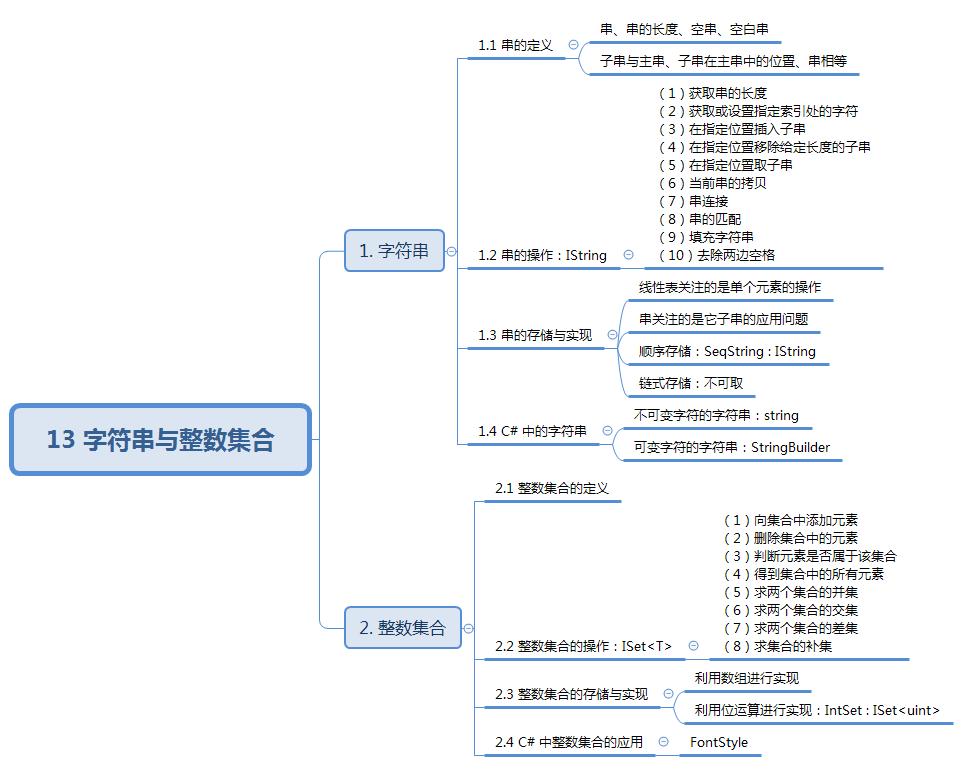
数据结构与算法:13 字符串与整数集合
13 字符串与整数集合 知识点: 1. 字符串 我们古人没有电影电视,没有游戏网络,所以文人们就会想出一些文字游戏来娱乐。比如宋代的李禺写了这样一首诗:“枯眼望遥山隔水,往来曾见几心知?壶空怕酌一杯酒&am…

是时候开始使用JavaScript严格模式了怎样启用javascri
E是时候开始使用JavaScript严格模式了怎样启用javascriCMAScript5将严格模式(strictmode)引入了Javascript中,目的是允许开发人员能够选择“更好”的Javascript版本,这个版本能用不同的方式处理那些普遍而又臭名昭著的错误。一开始的时候,我对…

Linux服务器日志备份到本地
1、确定线上服务器的日志文件名称和路径 2、一台本地服务器能连接公网,创建一个日志账户,设置密码 3、线上服务器要求: a、确定是否已安装sshpass包 [rootiZwz9ghdadtaey1msor7gnZ sh]# rpm -qa|grep sshpass sshpass-1.06-1.el7.x86_64 如不…

学习UI设计能做什么
UI设计这个岗位对于目前的很多企业来说是供不应求的,很多刚培训完UI设计的小伙伴,都不知道该如何定位自己的职能岗,那么学习UI设计能做什么呢?来看看下面小编的详细介绍就知道了。 学习UI设计能做什么? 1、图形设计/界面设计 软件产品的产品…
数据结构与算法:14 Leetcode同步练习(五)
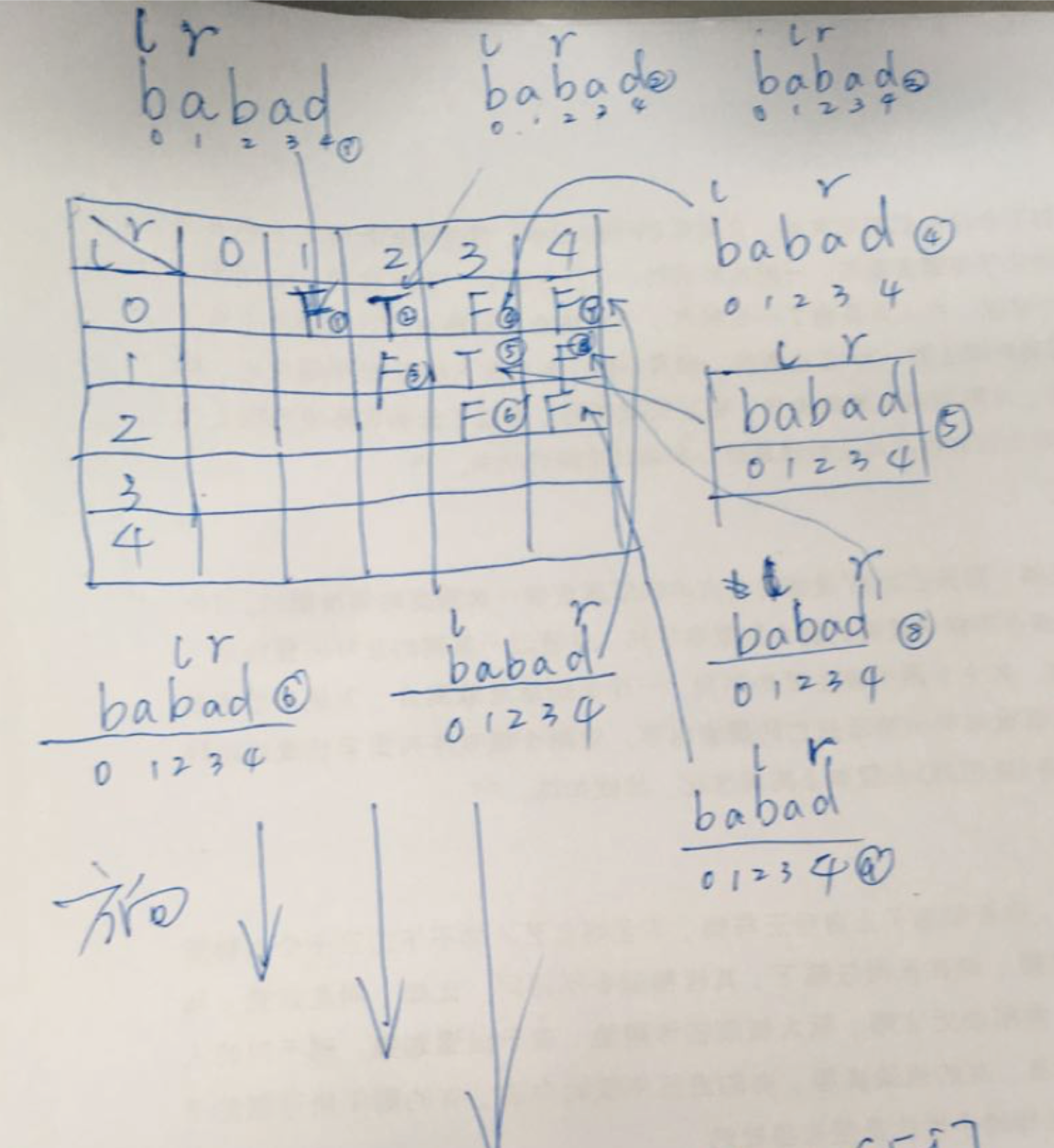
Leetcode同步练习(五) 目录 题目01:用栈实现队列题目02:托普利茨矩阵题目03:罗马数字转整数题目04:最长公共前缀题目05:反转字符串题目06:无重复字符的最长子串题目07:…

Oracle Spatial构建自定义投影坐标系
之前项目换过服务器,移植数据库时候并没有正确完整的移植自定义的投影坐标系,结果就报出莫名其妙的一些错误,比如unable to transform rectangle due to: ORA-13199: SRID does not exist。 因为在移植坐标系的时候仅仅只是将MDSYS.SDO_CRS_C…

php.ini 中开启短标签
控制参数: short_open_tag On如果设置为Off,则不能正常解析类似于这样形式的php文件:<?phpinfo()?>而只能解析<?phpphpinfo()?>这样形式的php文件所以要想php支持短标签,需要我们把short_open_tag 设置为On. 本…

参加UI培训就业多长时间
UI设计在近几年的发展前景是非常好的,越来越多的人都想要学习UI设计,目前大家比较想了解的是参加UI培训就业多长时间?来看看下面的详细介绍。 参加UI培训就业多长时间? 如今市面上的UI设计培训机构很多,选择一个口碑好靠谱的培训机构学习…
数据结构与算法:15 树
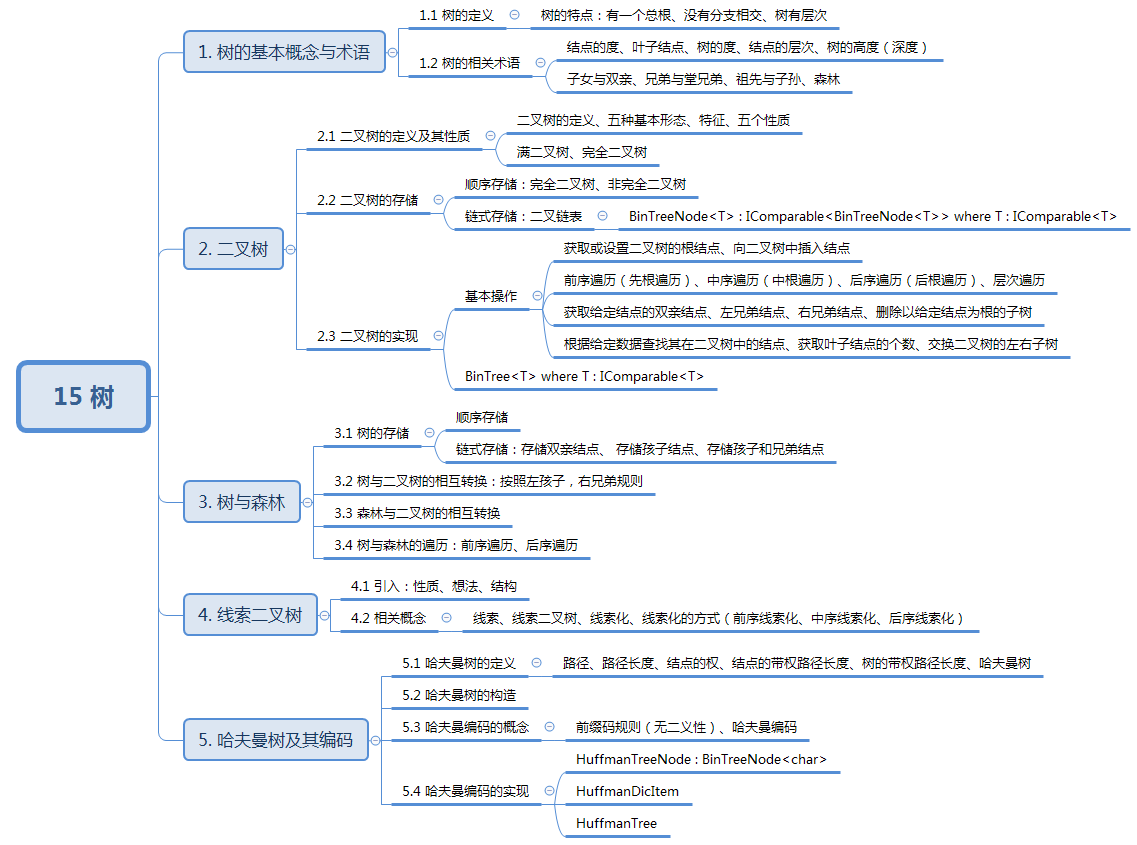
15 树 知识结构: 1. 树的基本概念与术语 1.1 树的定义 树是N(N≥0)N(N \geq 0)N(N≥0)个结点组成的有穷集合 ,该集合具有如下特征: (1)除N0N0N0的树外,有且仅有一个特定的称为根的结点。 (…

【as3】键盘事件
在AS3中,键盘事件是由KeyboardEvent类来处理的,属于flash.events包里面,有两种类型的键盘事件:KeyboardEvent.KEY_DOWN 和 KeyboardEvent.KEY_UP,对于键的代码获得我们通过keyCode这个属性 其实键盘事件使用起来还是相…

在后台代码中引入XAML的方法
本文将介绍三种方法用于在后台代码中动态加载XAML,其中有两种方法是加载已存在的XAML文件,一种方法是将包含XAML代码的字符串转换为WPF的对象。 这些是我在编写RegeX时获得的经验,它们将会给WPF程序带来更多的灵活性。 一、在资源字典中载入项…

JavaScript面向对象怎样删除标签页?
单击小标签右上角的按钮可D头删除标签页。其开发思路是,为“x”元素绑定单击事件,事件触发后,通过父元素1i获取索弓引值,然后用这个索引值将对应的li和section删除,并在删除后更新标签页的选中效电下面我们们就开始进行…

数据结构与算法:16 Leetcode同步练习(六)
Leetcode同步练习(六) 目录 题目01:相同的树题目02:对称二叉树题目03:二叉树的最大深度题目04: Pow(x, n)题目05:子集题目06:格雷编码题目07:二叉树的最近公共祖先题目…

Apache启动时报Could not reliably determine the server's fully qualified domain name
在系统启动时apache,没有启动起来,查看“事件查看器”发现报一些错误: The Apache service named reported the following error:>>> httpd.exe: Could not reliably determine the servers fully qualified domain name, using 19…

Windows Phone SDK update for Windows Phone 7.8
下载:http://www.microsoft.com/en-us/download/details.aspx?id36474 (在线安装) http://kuai.xunlei.com/d/cHbJCAIX4wBNVgFR5aa (离线下载 全语言 5.5G....) MS博客介绍:http://blogs.windows.com/windows_phone/b/wpdev/archive/2013/01/22/now-a…

作为一名合格的前端开发工程师需要会哪些
作为一名合格的前端开发工程师需要会哪些?web前端要学习的内容有很多,想要成为一名合格的web前端工程师,综合实力是要非常强的,来看看下面的详细介绍吧。 作为一名合格的前端开发工程师需要会哪些?前端开发工程师不仅要掌握基本的前端开发技…
memcached部署
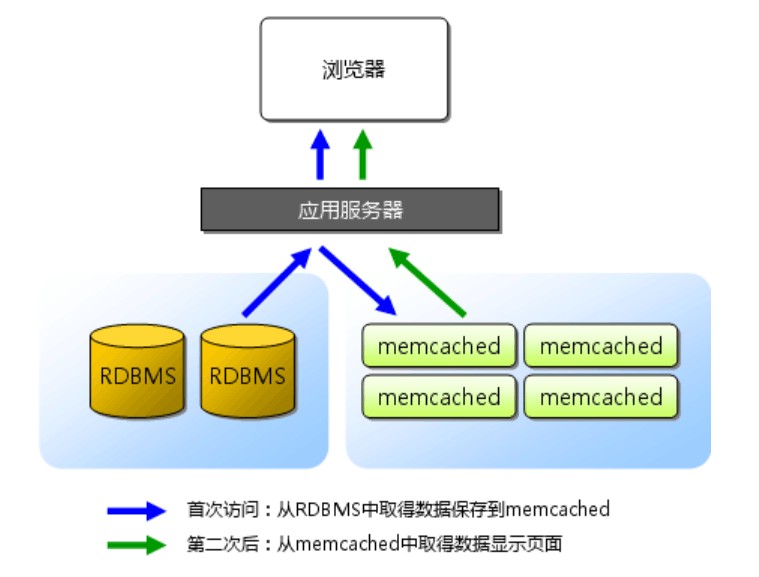
第1章 memcached 1 memcached前言 1.1 memcached诞生的原因 2003年诞生了memcached Web1.0 2005以前 企业提供内容为主。 Web2.02005-2012 企业只提供平台,用户参与上传下载内容。 memcached 内存缓存软件,内存比磁盘快。 传统场景中,多数…

线性代数:第二章 矩阵及其运算
本讲义是自己上课所用幻灯片,里面没有详细的推导过程(笔者板书推导)只以大纲的方式来展示课上的内容,以方便大家下来复习。 本章主要介绍有关矩阵的知识,主要包括矩阵的基本运算(加法、数乘、乘法、乘幂、…

sdut 2401 最大矩形面积
1http://acm.sdut.edu.cn/sdutoj/problem.php?actionshowproblem&problemid2401 /*2 最大矩形面积,把边界点加上3 从左往右 处理一遍;4 再从上往下处理一遍;5 */6 7 #include<stdio.h>8 #define maxn 200009 #include<cmath>…
Python中怎样改变集合之间的关系?
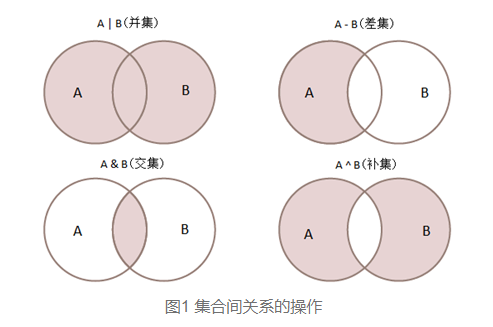
Python中怎样改变集合之间的关系?数学中,两个集合关系的常见操作包括:交集、并集、差集、补集。设A,B是两个集合,集合关系的操作介绍如下: 交集是指属于集合A且属于集合B的元素所组成的集合, 并集是指集合…
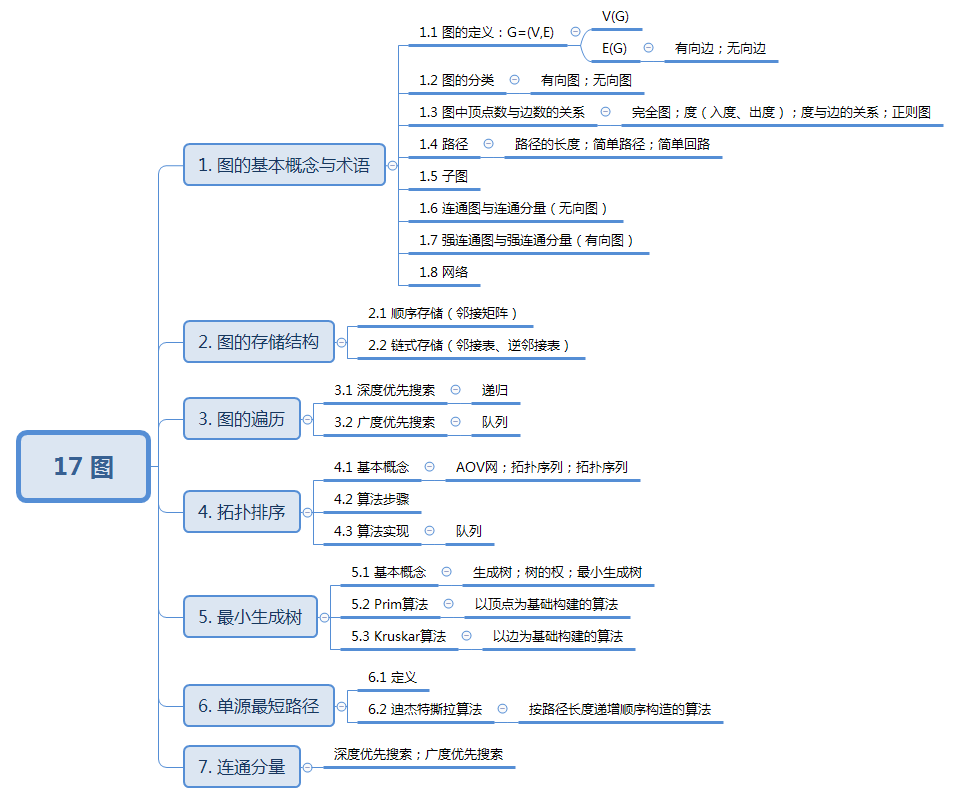
数据结构与算法:17 图
17 图 知识结构: 1. 图的基本概念与术语 1.1 图的定义 图由顶点集和边集组成,记为G(V,E)G(V,E)G(V,E)。 顶点集:顶点的有穷非空集合,记为V(G)V(G)V(G)。边集:顶点偶对的有穷集合,记为E(G)E(G)E(G) 。 …

云计算安全:技术与应用
云计算安全:技术与应用中国电信网络安全实验室 编著ISBN 978-7-121-14409-72012年1月出版定价:59.00元16开236页宣传语:全面了解云计算安全风险、安全防护手段的佳作!内 容 简 介随着云计算的兴起,安全成为云计算能否顺…

再谈HOST文件
前几天弄了一个关于禁止打开某个网站的文章后,觉得这个HOST文件真的挺有意思的。并且也总是想把自己对它新的理解写下来(也许大家都明白了)以下是HOST文件的内容:# Copyright (c) 1993-1999 Microsoft Corp.## This is a sample H…

PMP®考试是什么机构
项目管理对于很多职场中的人来说是以后要发展的一个方向,随着各职业内卷也越来越严重,pmp认证引起了大家的关注,有朋友问:PMP考试是什么机构?下面我们给大家介绍一下。 PMP考试是什么机构?PMP考试认证在我国大陆地区需要三方机构…
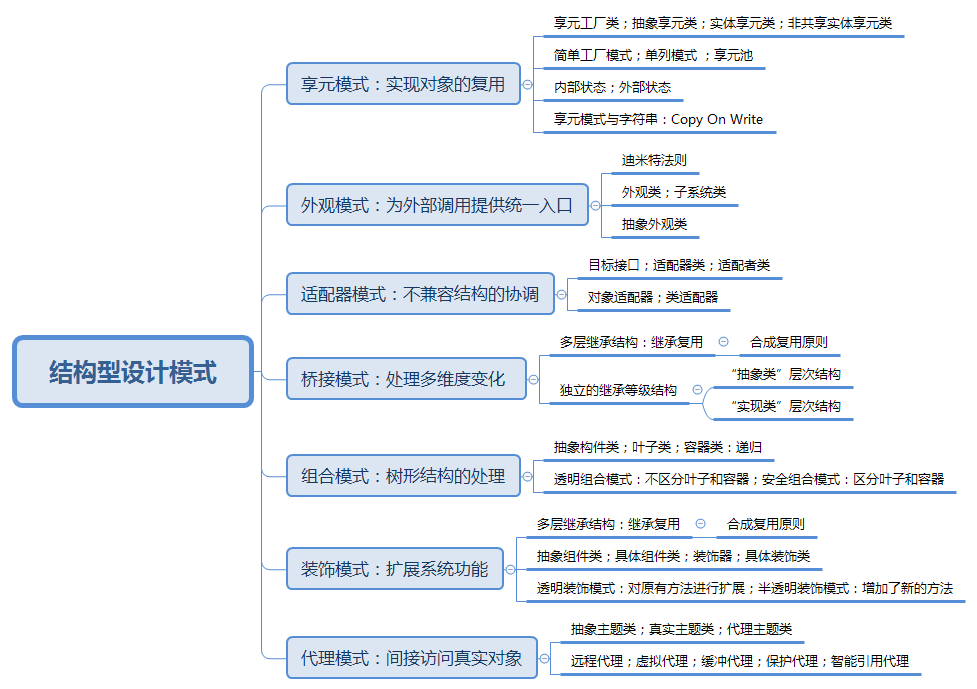
技术图文:03 结构型设计模式(上)
结构型设计模式(上) 本教程主要介绍一系列用于如何将现有类或对象组合在一起形成更加强大结构的经验总结。 知识结构: 享元模式 – 实现对象的复用 Sunny 软件公司欲开发一个围棋软件,其界面效果如下图所示: 图2 围…

Linux抓包工具tcpdump详解
原文链接 tcpdump是一个用于截取网络分组,并输出分组内容的工具,简单说就是数据包抓包工具。tcpdump凭借强大的功能和灵活的截取策略,使其成为Linux系统下用于网络分析和问题排查的首选工具。 tcpdump提供了源代码,公开了接口&…

学习笔记TF065:TensorFlowOnSpark
2019独角兽企业重金招聘Python工程师标准>>> Hadoop生态大数据系统分为Yam、 HDFS、MapReduce计算框架。TensorFlow分布式相当于MapReduce计算框架,Kubernetes相当于Yam调度系统。TensorFlowOnSpark,利用远程直接内存访问(Remote Direct Memo…
